4.2. Жидкость с малой вязкостью, когда 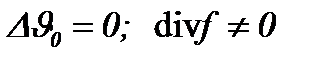
I . Цель пункта заключается в модификации метода (4.2), которая позволит получить аналитическое решение задачи Навье-Стокса с вязкостью в 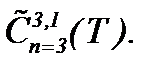
Если компоненты начальной скорости и функции 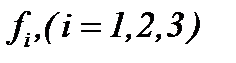 подчиняются условиям
подчиняются условиям
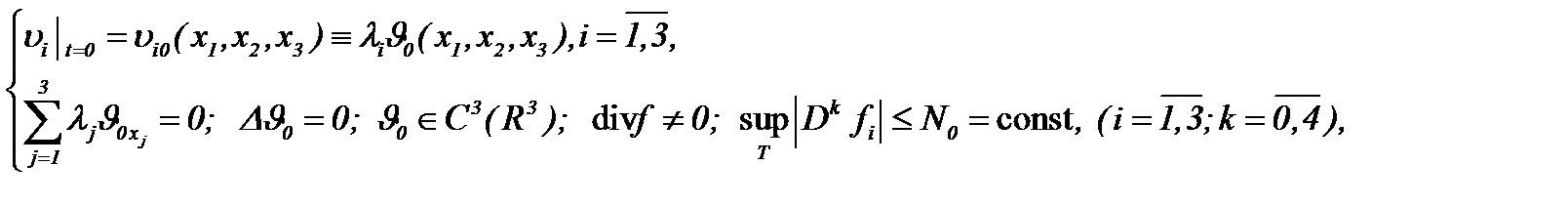 (4.11)
(4.11)
то применимы преобразования вида
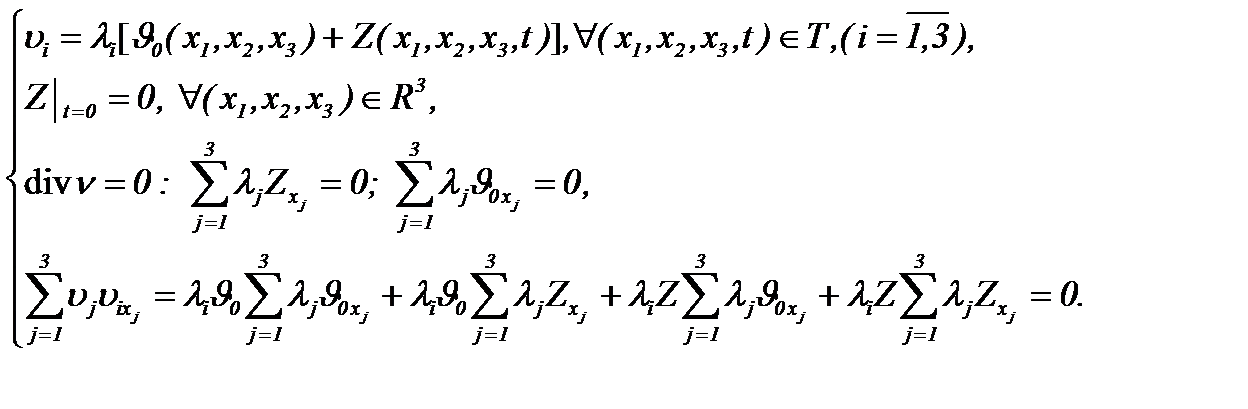 (4.12)
(4.12)
Тогда система (1.1) эквивалентно трансформируется к виду
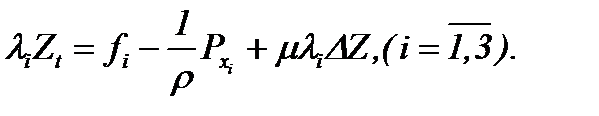 (4.13)
(4.13)
Применяя разработанный выше алгоритм АПС к системе (4.13) с условиями (4.11) и (4.12), имеем относительно давления следующее уравнение
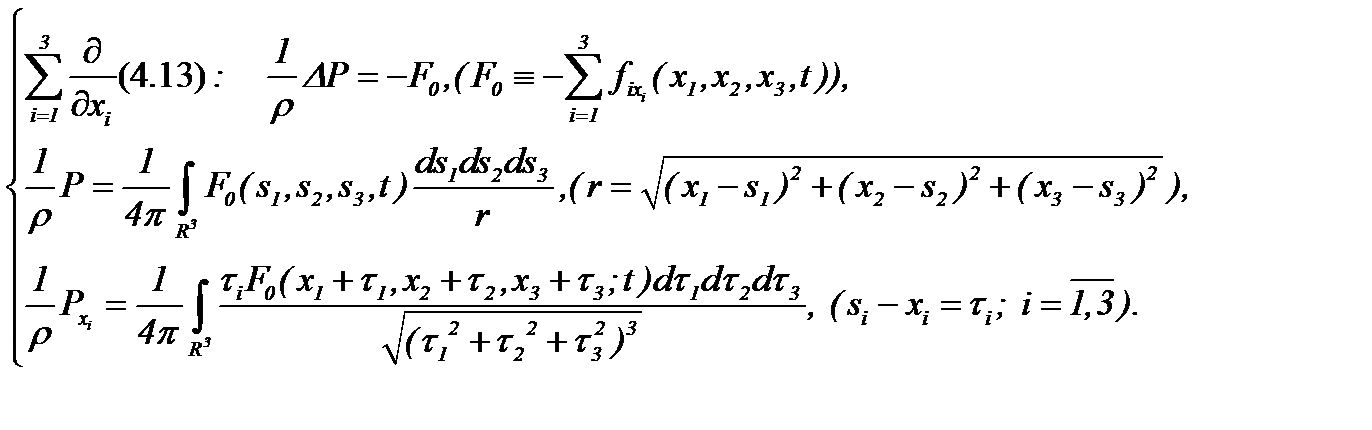 (4.14)
(4.14)
Значит, система (4.13) преобразуется к виду
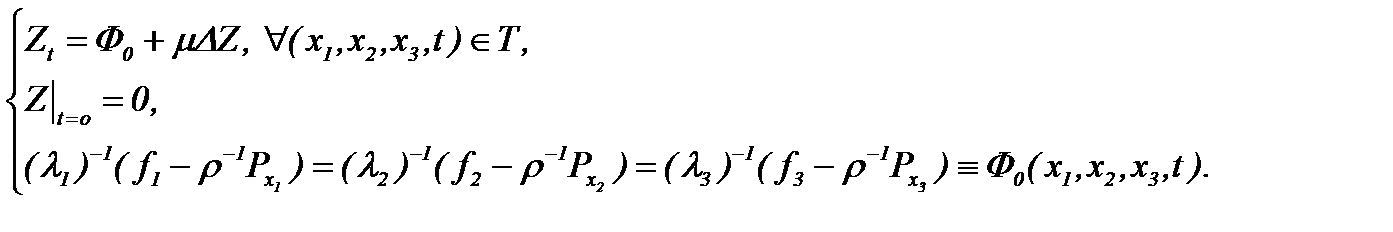 (4.13)*
(4.13)*
Тогда решение задачи (4.13)* представимо в виде
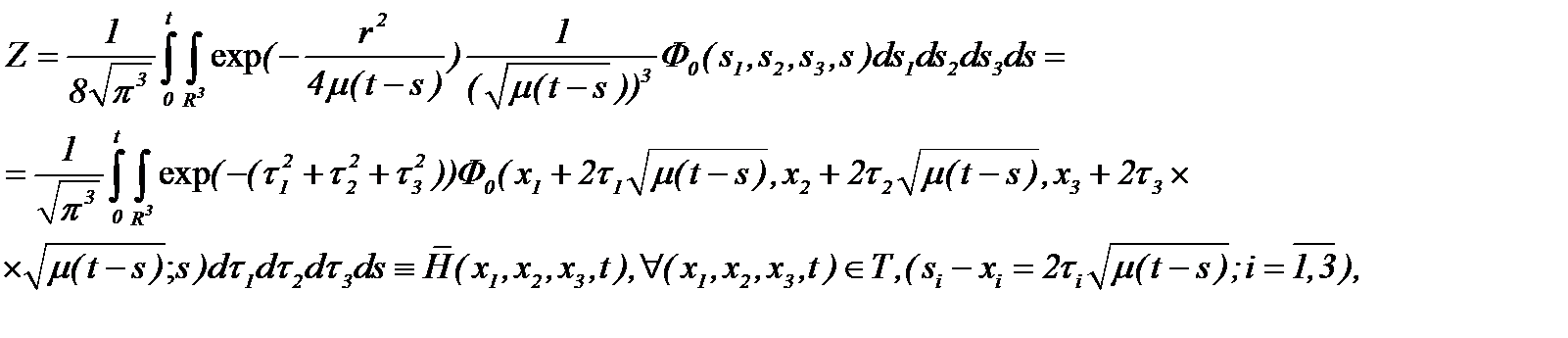 (4.15)
(4.15)
где 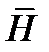 – известная функция, а потому решение (4.15) удовлетворяет задачу (4.13)*.
– известная функция, а потому решение (4.15) удовлетворяет задачу (4.13)*.
Действительно, определив частные производные уравнения (4.15)
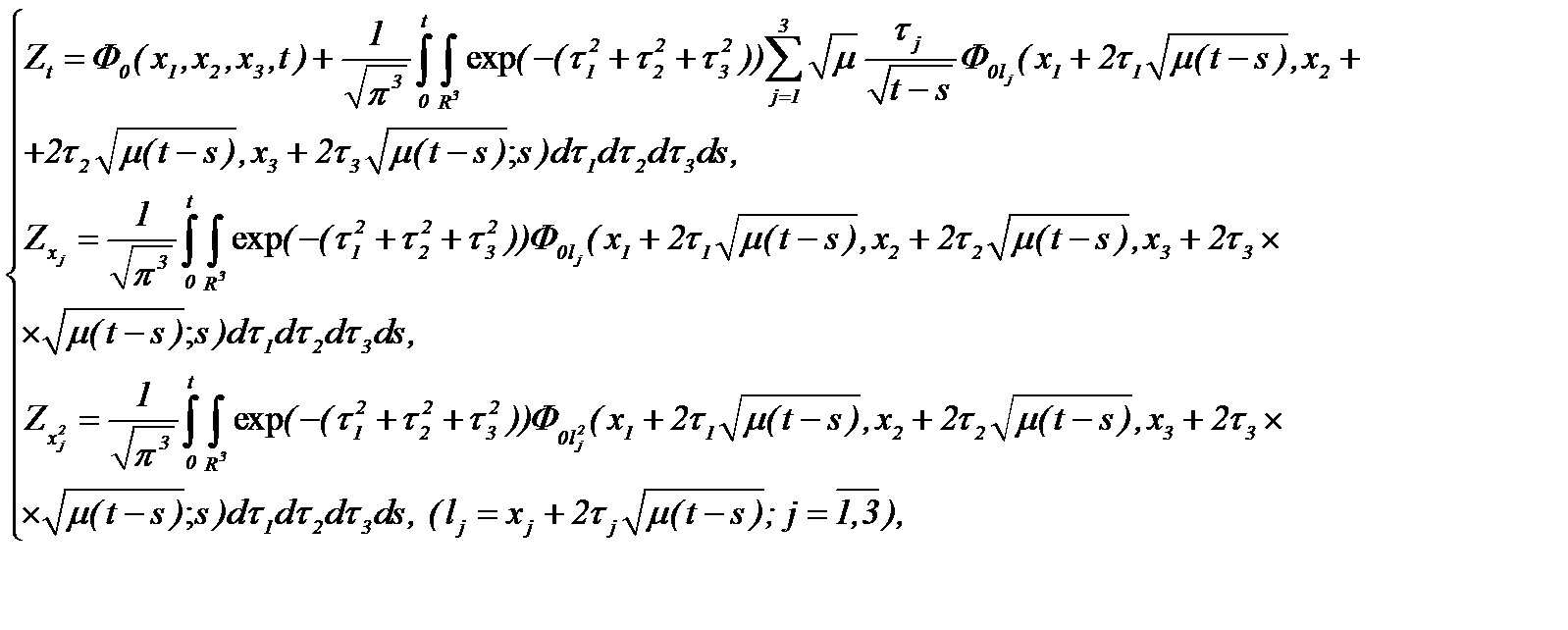 (4.16)
(4.16)
а, затем, подставив (4.16) в (4.13)*, получим
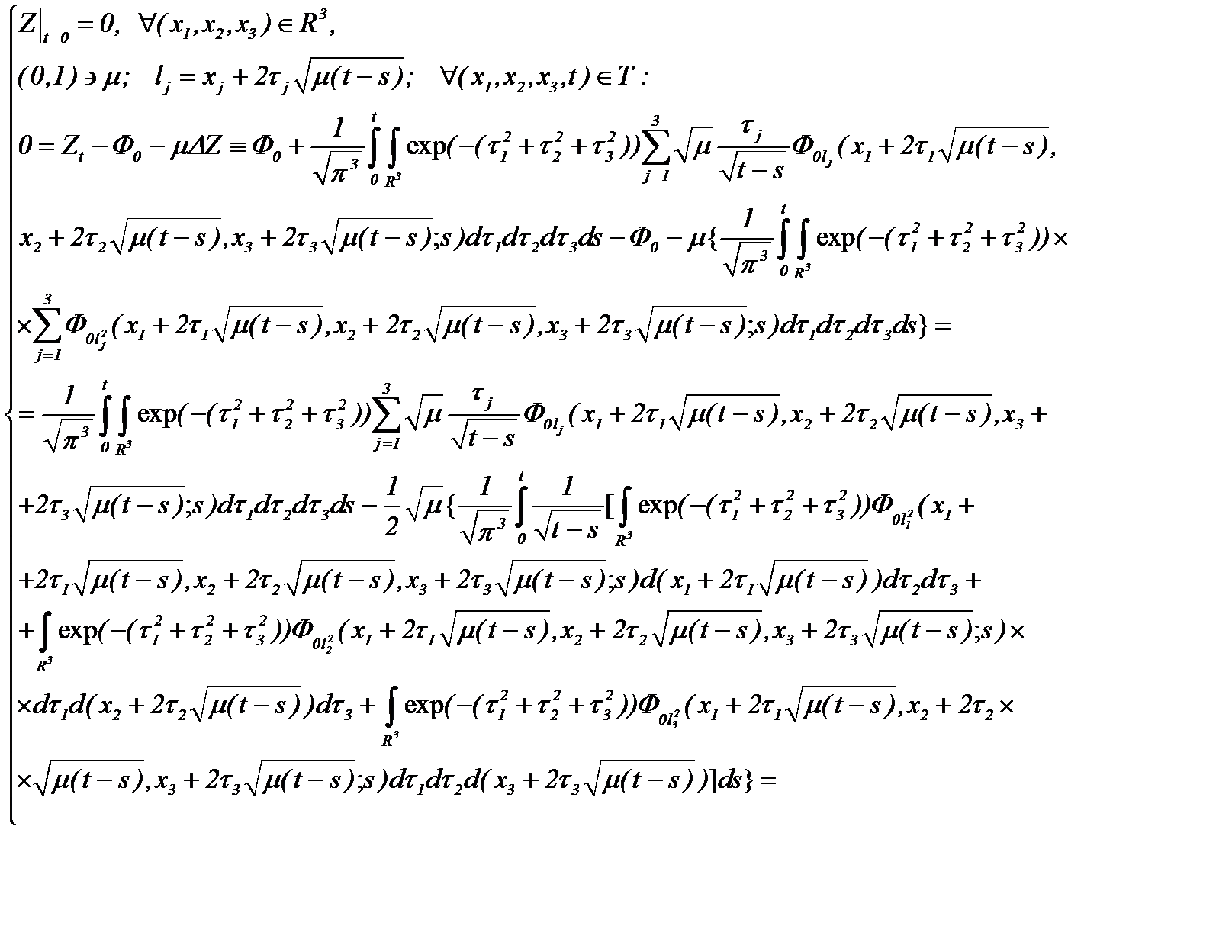
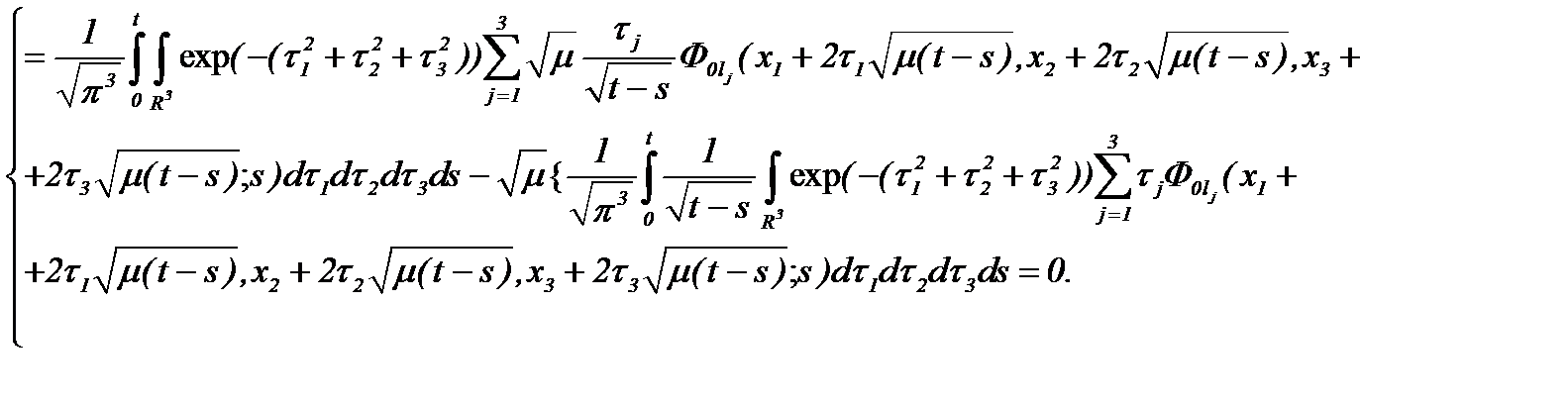
Таким образом, получено то, что и требовалось показать.
Из полученного результата следует, что функции 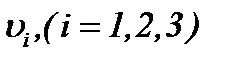 определяются преобразованиями (4.12), т.е.
определяются преобразованиями (4.12), т.е.
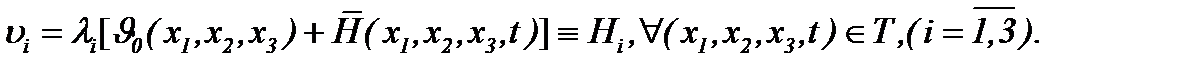 (4.17)
(4.17)
Поэтому, учитывая частные производные первого порядка системы (4.17) и подводя итог с принятием во внимание (1.2) и (4.12), имеем
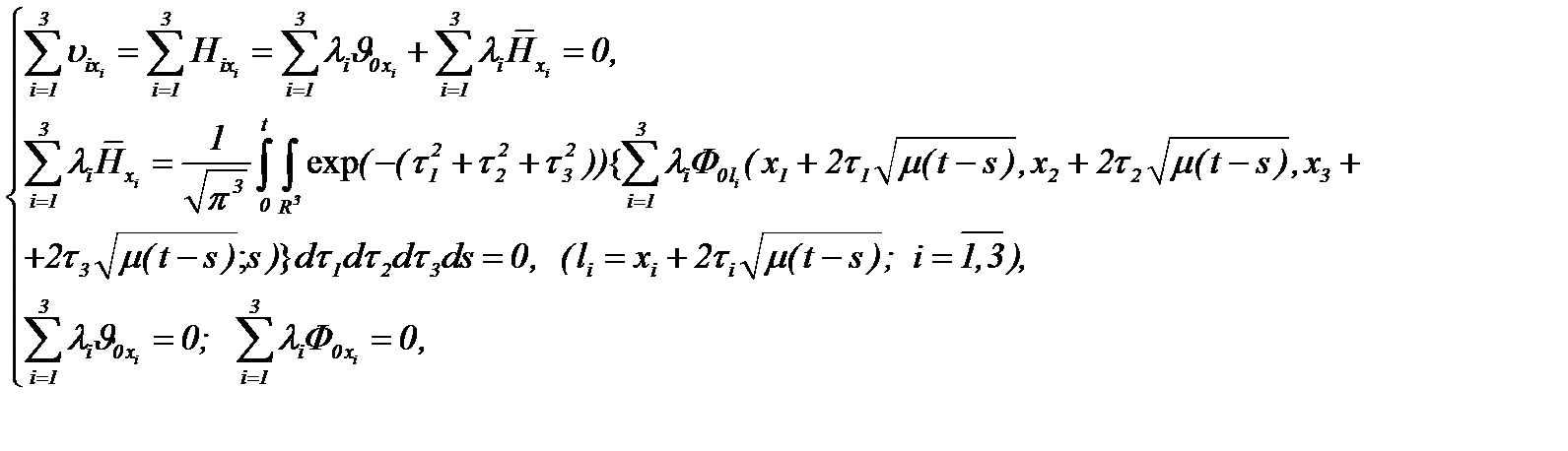
значит, система (4.17) удовлетворяет условию (1.2).
II . Так как 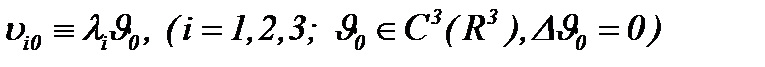 , то решение задачи (1.1) – (1.3) принадлежит
, то решение задачи (1.1) – (1.3) принадлежит 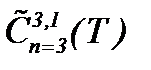 :
:
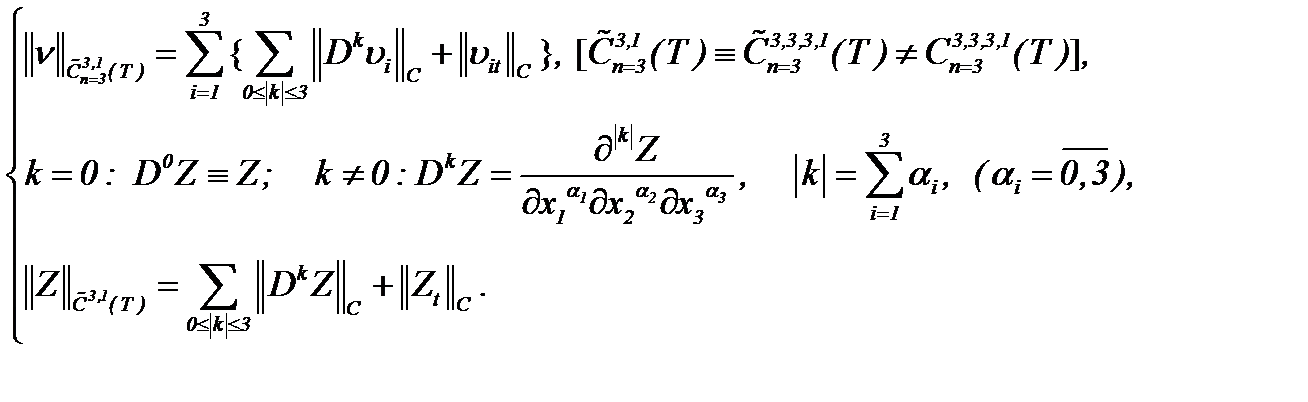
Очевидно, если
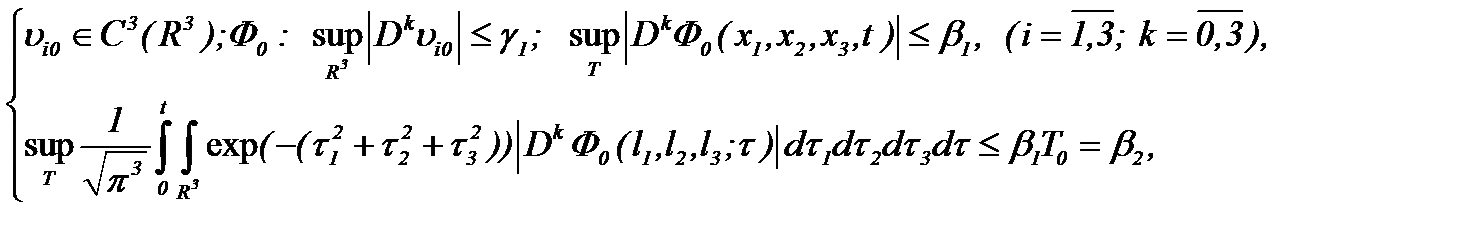
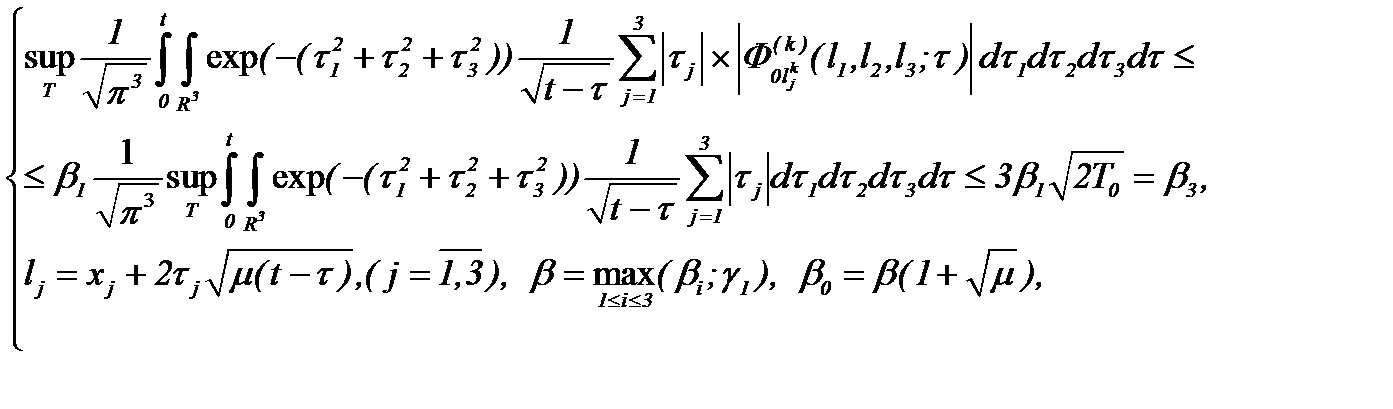 (4.18)
(4.18)
то на основании (4.15) получим неравенство
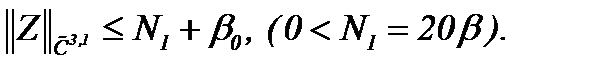
В классе функций 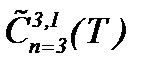 , таким образом, оценка (4.17) дает необходимый результат
, таким образом, оценка (4.17) дает необходимый результат
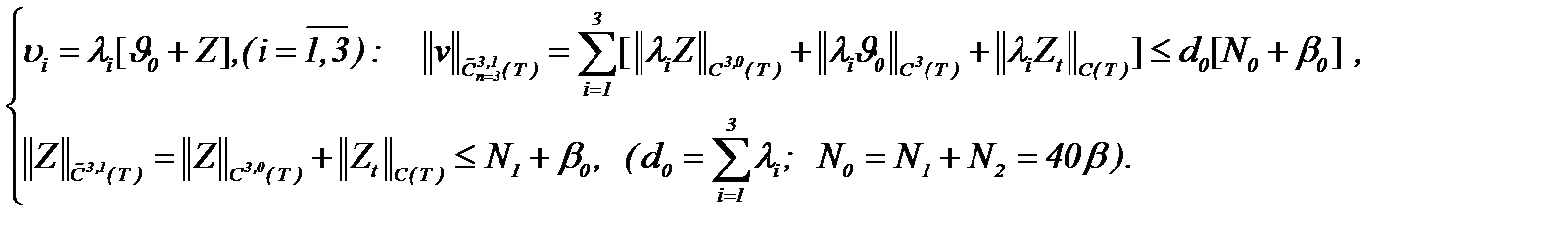
Лемма 2. Уравнение (4.15) с условиями (1.2), (4.11), (4.12) и (4.18) имеет единственное решение в 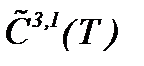 .
.
Теорема 4*. При выполнении условий леммы 2 задача (1.1), (1.2), (4.11) разрешима в 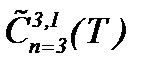 и решение определяется правилом (4.17).
и решение определяется правилом (4.17).
Итогом исследований данного пункта являются результаты теоремы 4*, где решение системы (1.1) рассматривается как строгое решение задачи (1.1) – (1.3) в 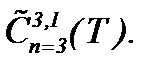 Очевидно, малые изменения
Очевидно, малые изменения 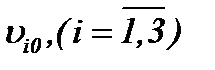 или
или 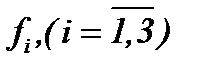 незначительно влияют на решение (4.17), значит, решение непрерывно зависит от этих данных. Поэтому вопрос о корректной постановке задачи (1.1) – (1.3) решается, исходя из результатов теоремы 4*.
незначительно влияют на решение (4.17), значит, решение непрерывно зависит от этих данных. Поэтому вопрос о корректной постановке задачи (1.1) – (1.3) решается, исходя из результатов теоремы 4*.
Замечание 2. Результаты пункта 4.2 с учетом преобразования (4.12) могут быть использованы в отношении уравнений Навье-Стокса (1.1)
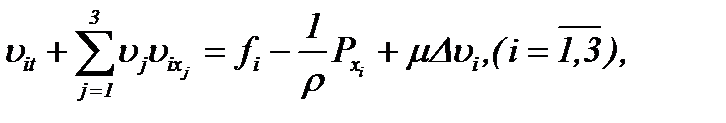 (1)
(1)
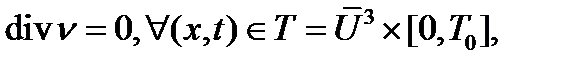 (2)
(2)
т.е. в области 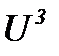 пространства переменных
пространства переменных 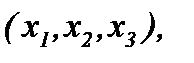 ограниченных поверхностью
ограниченных поверхностью 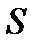 , где t удовлетворяет неравенству
, где t удовлетворяет неравенству 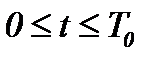 при известных условиях [13]
при известных условиях [13]
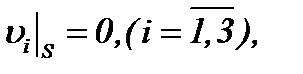 (3)
(3)
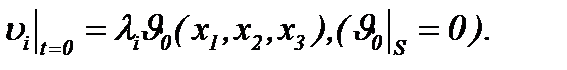 (4)
(4)
Действительно, применяя преобразование (4.12), т.е.
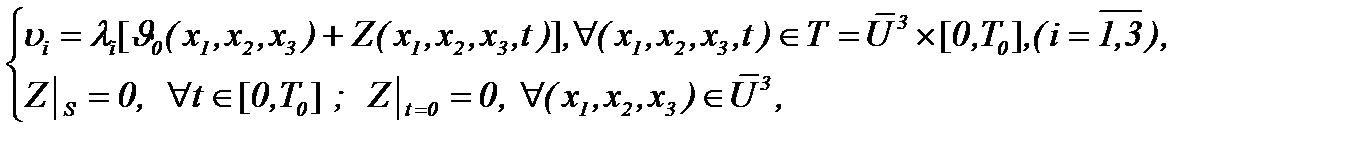 (5)
(5)
из (1) получим уравнение (4.13), а именно
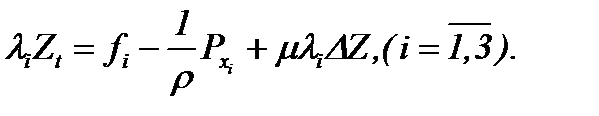 (6)
(6)
Откуда следует уравнение (4.14) в виде
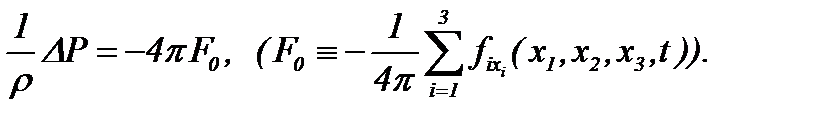 (7)
(7)
Поскольку уравнение (7) является уравнением Пуассона, то для сравнения рассмотрим краевую задачу следующего вида
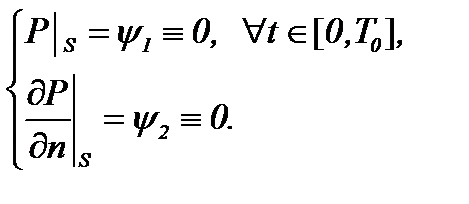 (8)
(8)
Тогда из уравнения (7) получаем выражение для неизвестного давления 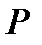
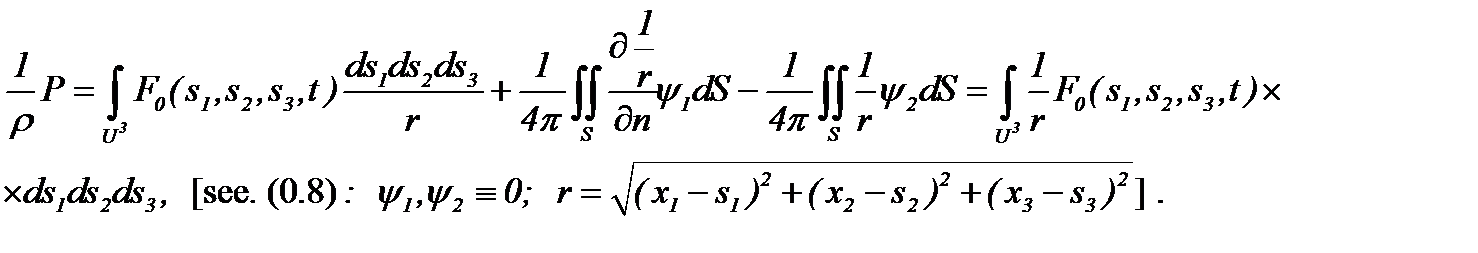 (9)
(9)
Теперь, учитывая (6) и (9), имеем
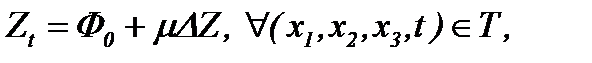 (10)
(10)
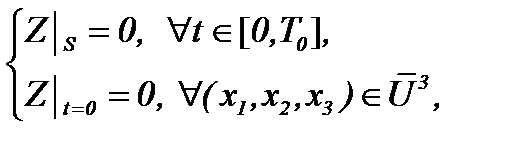 (11)
(11)
где
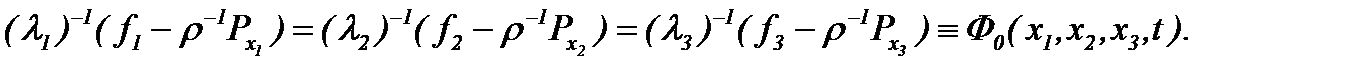
Полученного результата достаточно, чтобы, не вдаваясь в полное исследование задачи (10), (11), которое дано в [13, с. 349-351], ограничится тем, что обобщенное решение принимается, как решение в обычном смысле при достаточной гладкости 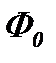 [13, стр.311-318, XXII]. Поэтому подобные выводы справедливы в отношении задачи (1) – (4), что и требовалось доказать.
[13, стр.311-318, XXII]. Поэтому подобные выводы справедливы в отношении задачи (1) – (4), что и требовалось доказать.
Замечание 3. В пункте 2.2 приведено неравенство Билла-Като-Мажда. Поэтому, здесь укажем связь критерий регулярности Билла-Като-Мажда с результатами теоремы 4*, так как результаты этой теоремы приводят к глобальным классическим решениям уравнений Навье-Стокса (1.1) в классе 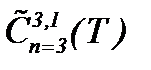 с точки зрения исходных данных, удовлетворяющих (4.17). Следовательно, при выполнении условий теоремы 4*, а также
с точки зрения исходных данных, удовлетворяющих (4.17). Следовательно, при выполнении условий теоремы 4*, а также
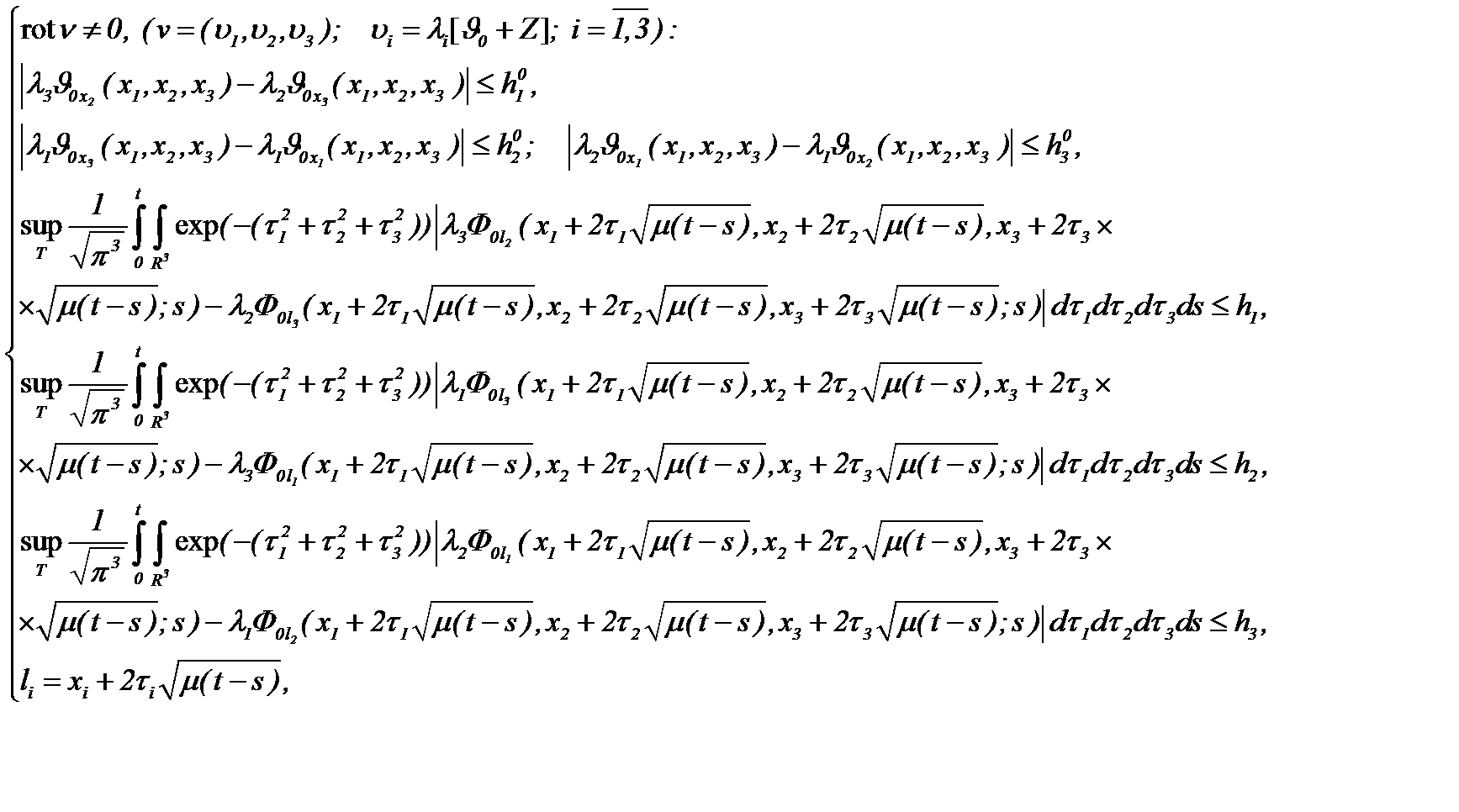
имеет место
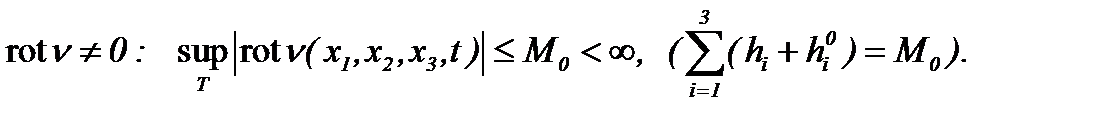 (4.19)
(4.19)
Как следствие, получим, аналогично формуле (2.24), оценку
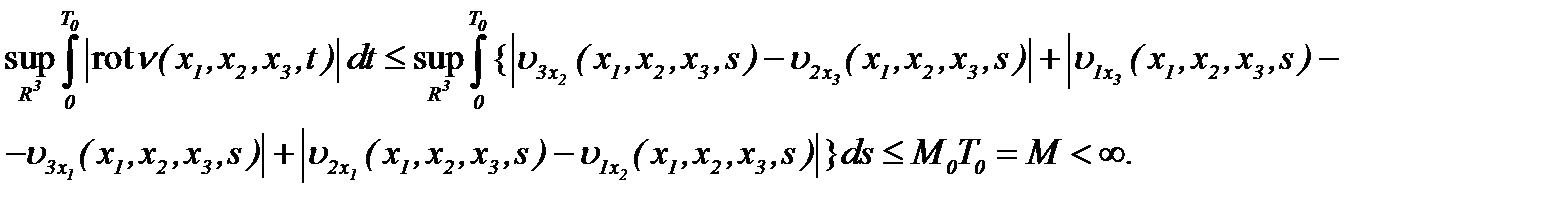 (4.20)
(4.20)
Значит, выведенная нами оценка является оценкой типа Билла-Като-Мажда [5].





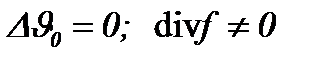
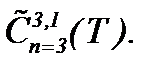
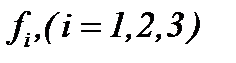 подчиняются условиям
подчиняются условиям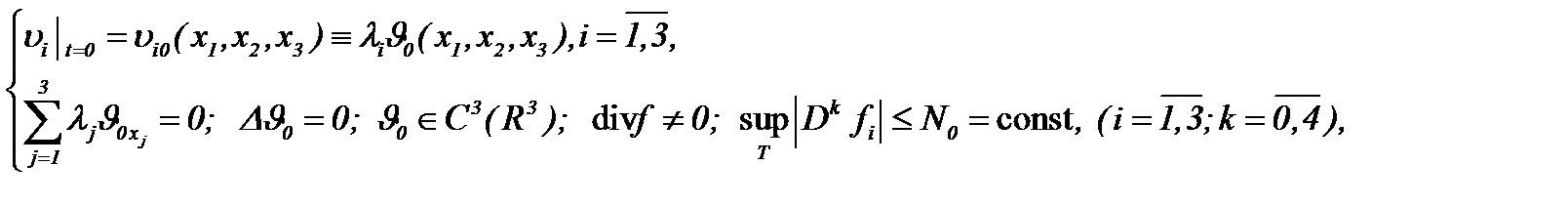 (4.11)
(4.11)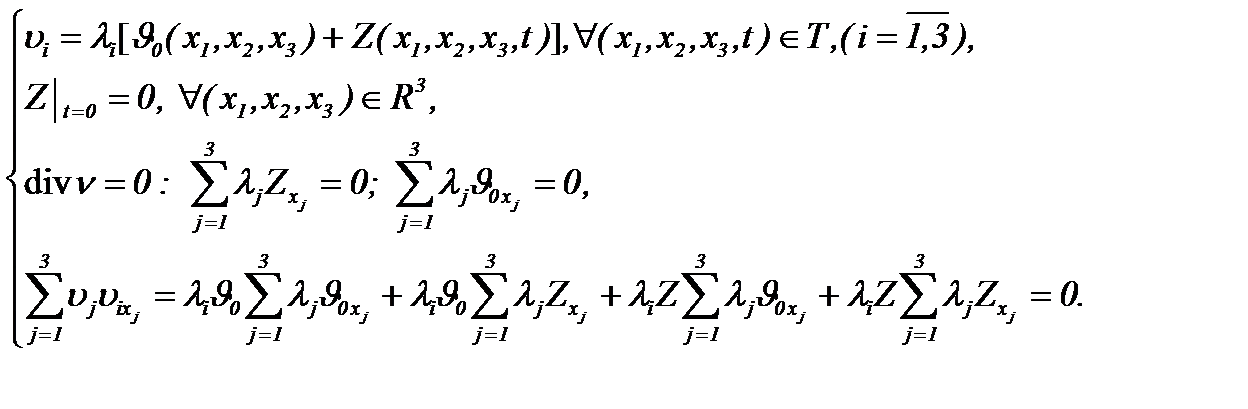 (4.12)
(4.12)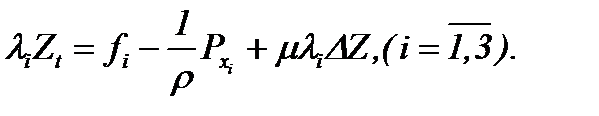 (4.13)
(4.13)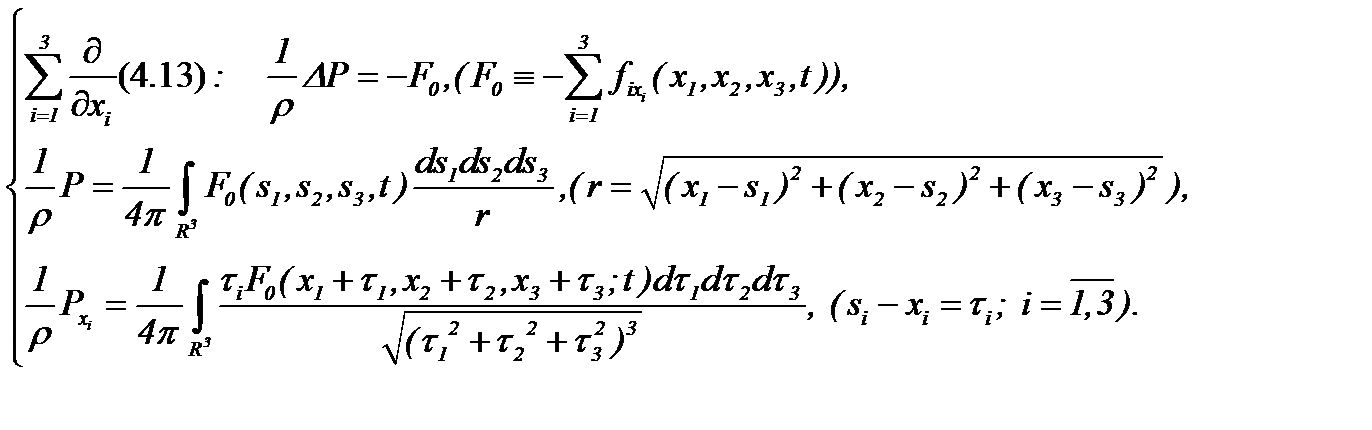 (4.14)
(4.14)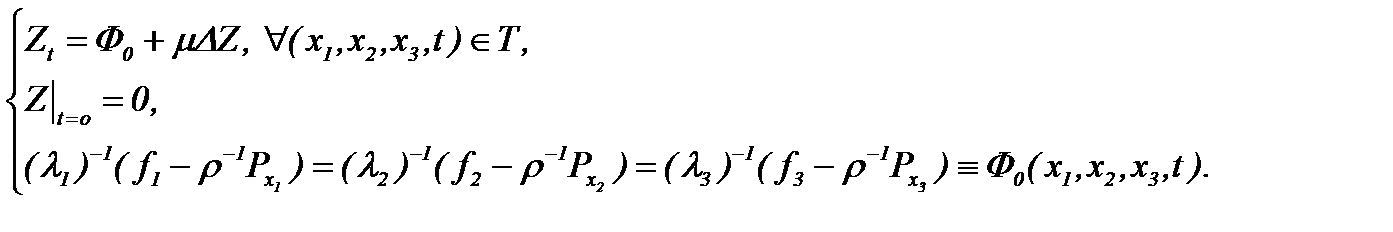 (4.13)*
(4.13)*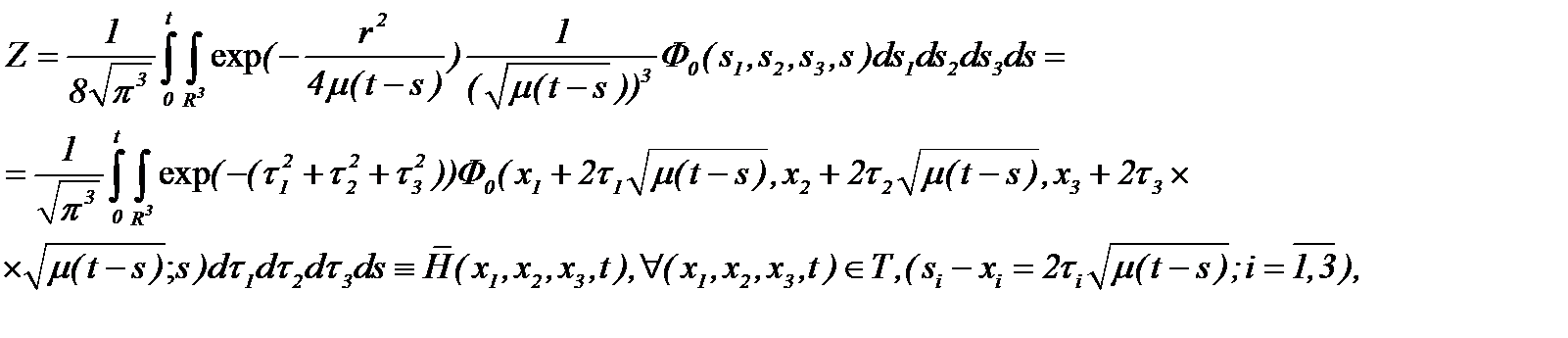 (4.15)
(4.15) – известная функция, а потому решение (4.15) удовлетворяет задачу (4.13)*.
– известная функция, а потому решение (4.15) удовлетворяет задачу (4.13)*.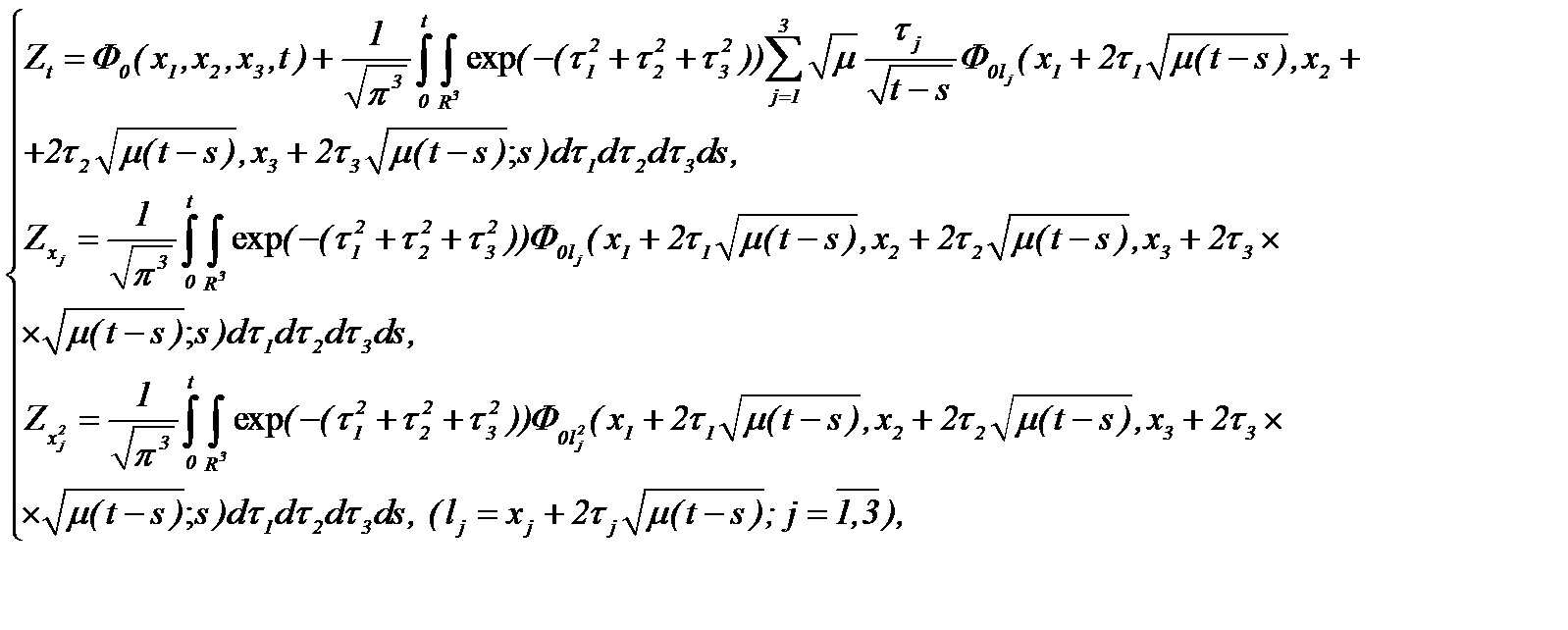 (4.16)
(4.16) 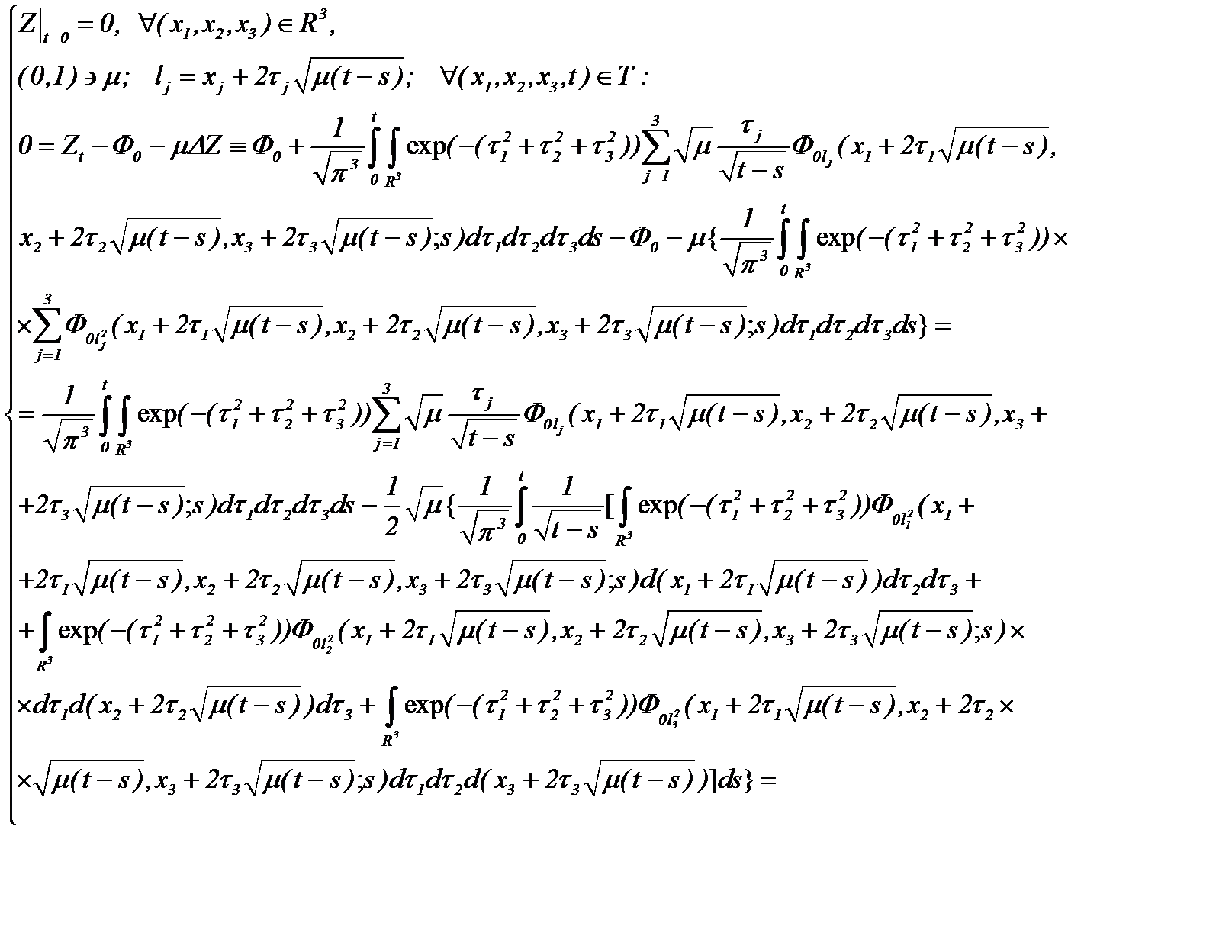
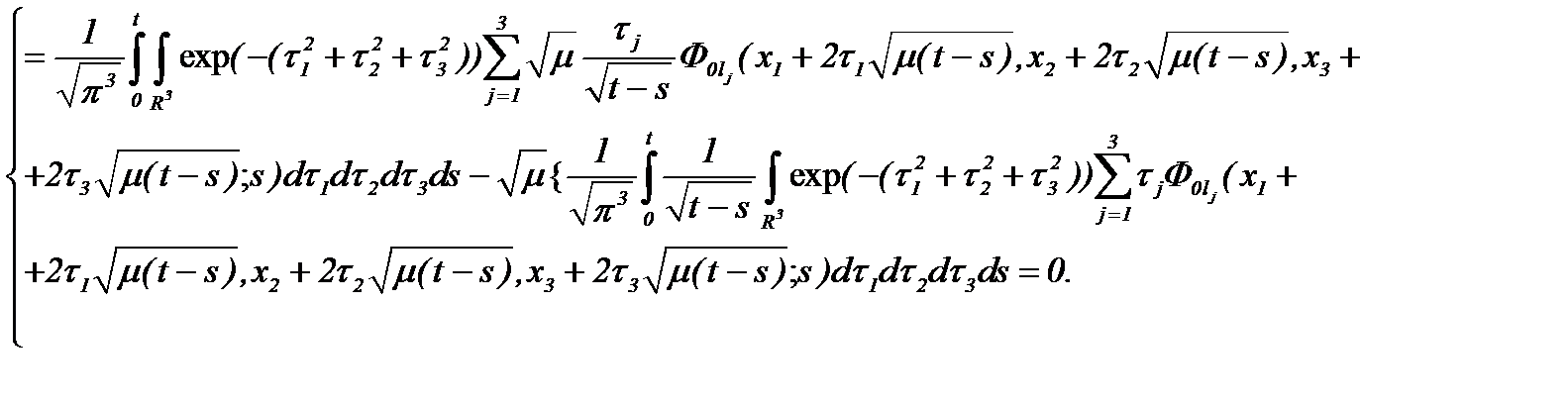
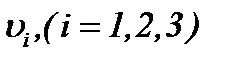 определяются преобразованиями (4.12), т.е.
определяются преобразованиями (4.12), т.е.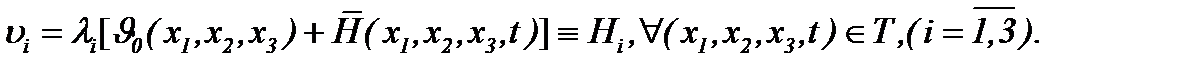 (4.17)
(4.17)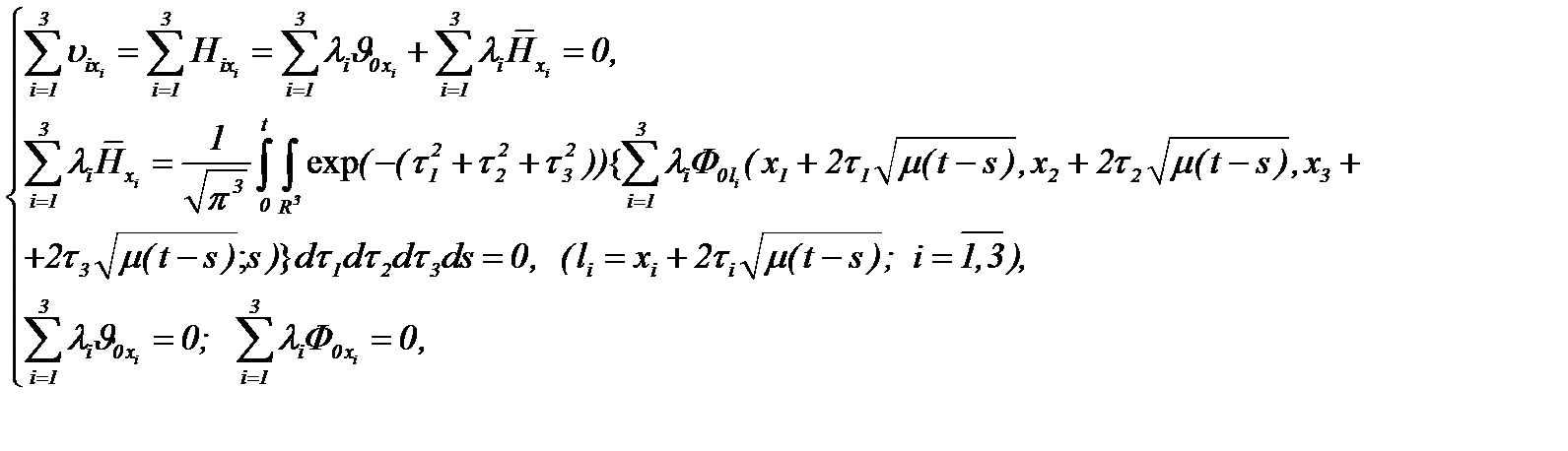
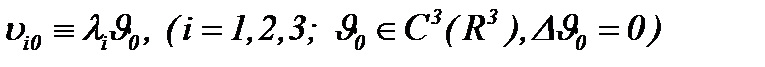 , то решение задачи (1.1) – (1.3) принадлежит
, то решение задачи (1.1) – (1.3) принадлежит 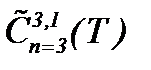 :
: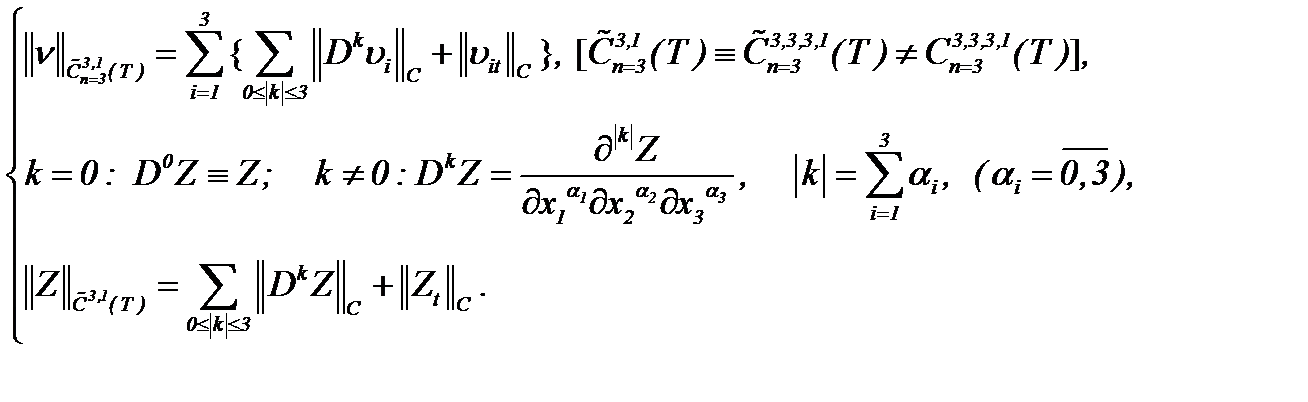
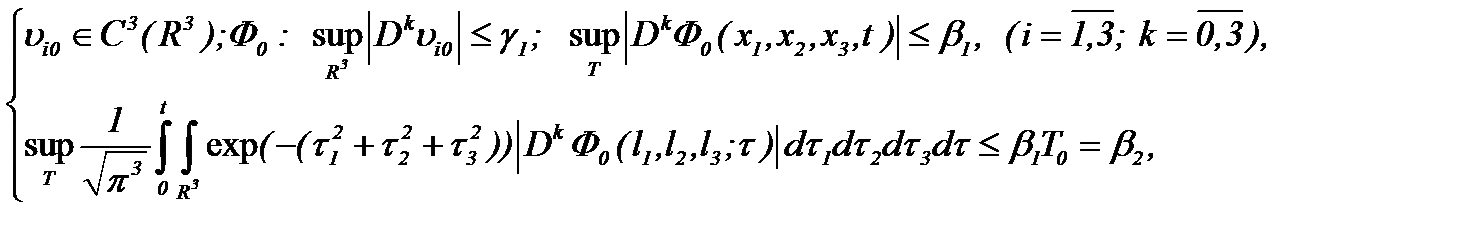
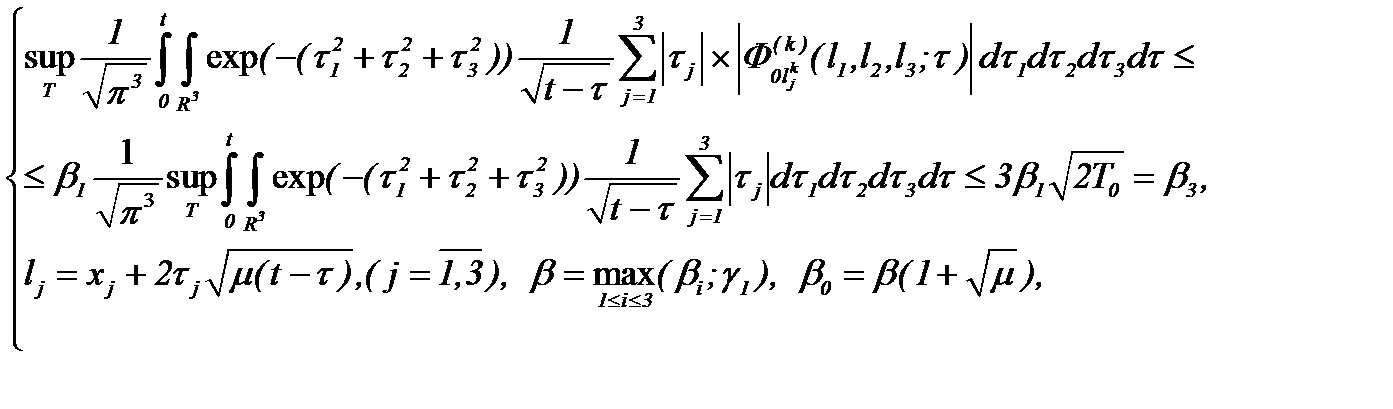 (4.18)
(4.18)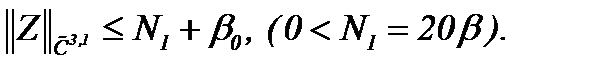
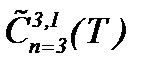 , таким образом, оценка (4.17) дает необходимый результат
, таким образом, оценка (4.17) дает необходимый результат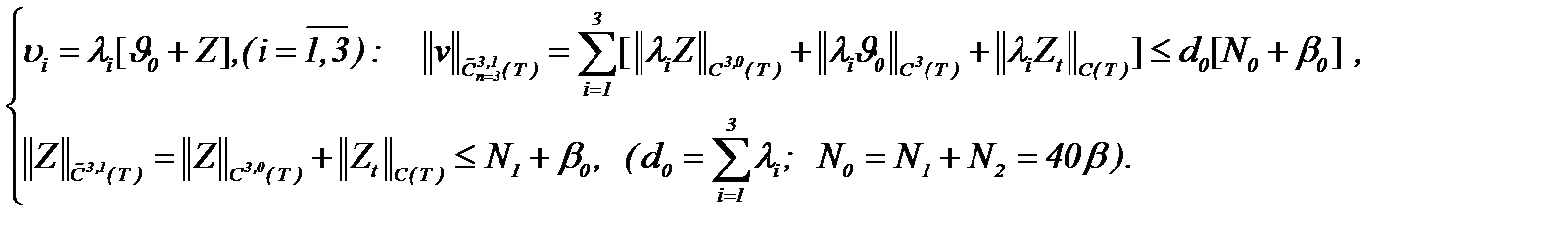
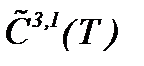 .
.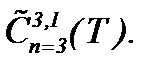 Очевидно, малые изменения
Очевидно, малые изменения 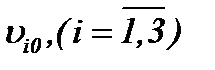 или
или 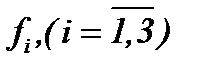 незначительно влияют на решение (4.17), значит, решение непрерывно зависит от этих данных. Поэтому вопрос о корректной постановке задачи (1.1) – (1.3) решается, исходя из результатов теоремы 4*.
незначительно влияют на решение (4.17), значит, решение непрерывно зависит от этих данных. Поэтому вопрос о корректной постановке задачи (1.1) – (1.3) решается, исходя из результатов теоремы 4*.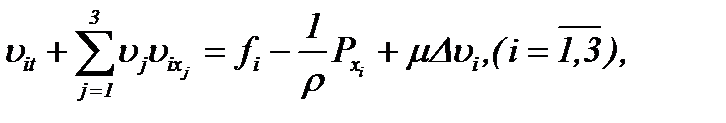 (1)
(1)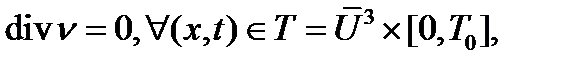 (2)
(2)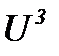 пространства переменных
пространства переменных 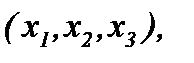 ограниченных поверхностью
ограниченных поверхностью 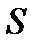 , где t удовлетворяет неравенству
, где t удовлетворяет неравенству 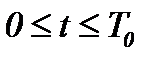 при известных условиях [13]
при известных условиях [13]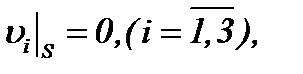 (3)
(3)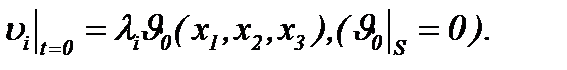 (4)
(4)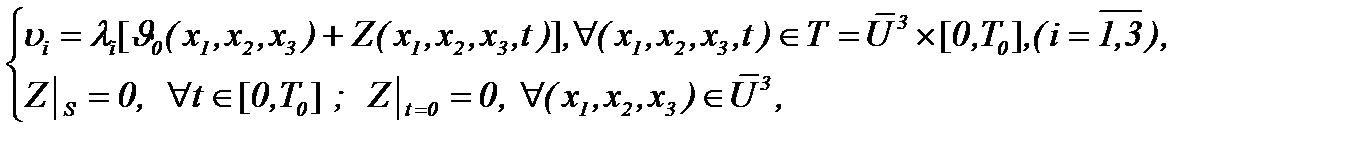 (5)
(5)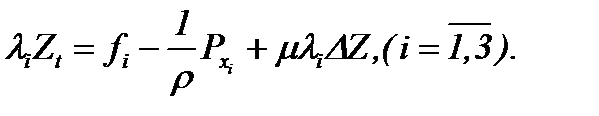 (6)
(6)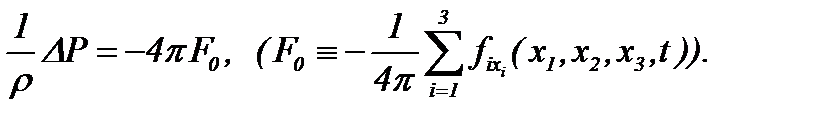 (7)
(7)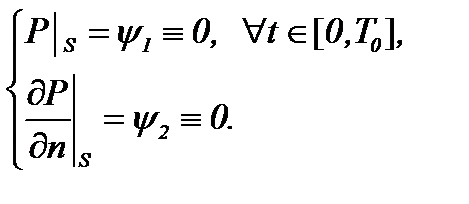 (8)
(8)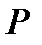
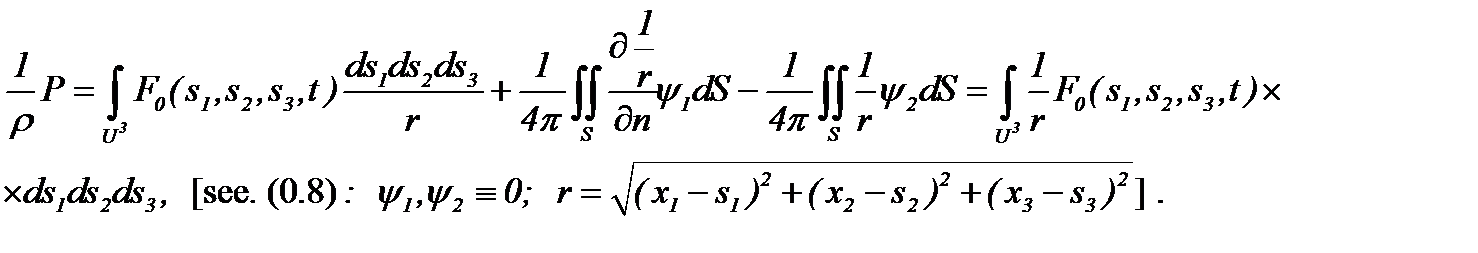 (9)
(9) 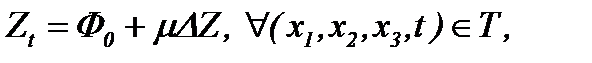 (10)
(10)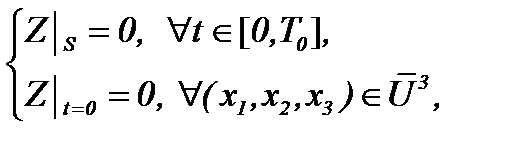 (11)
(11)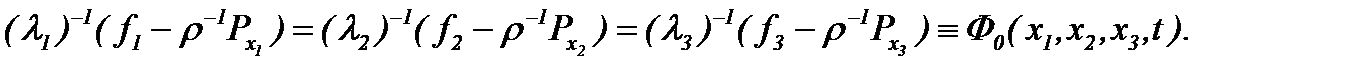
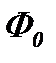 [13, стр.311-318, XXII]. Поэтому подобные выводы справедливы в отношении задачи (1) – (4), что и требовалось доказать.
[13, стр.311-318, XXII]. Поэтому подобные выводы справедливы в отношении задачи (1) – (4), что и требовалось доказать.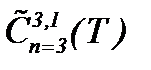 с точки зрения исходных данных, удовлетворяющих (4.17). Следовательно, при выполнении условий теоремы 4*, а также
с точки зрения исходных данных, удовлетворяющих (4.17). Следовательно, при выполнении условий теоремы 4*, а также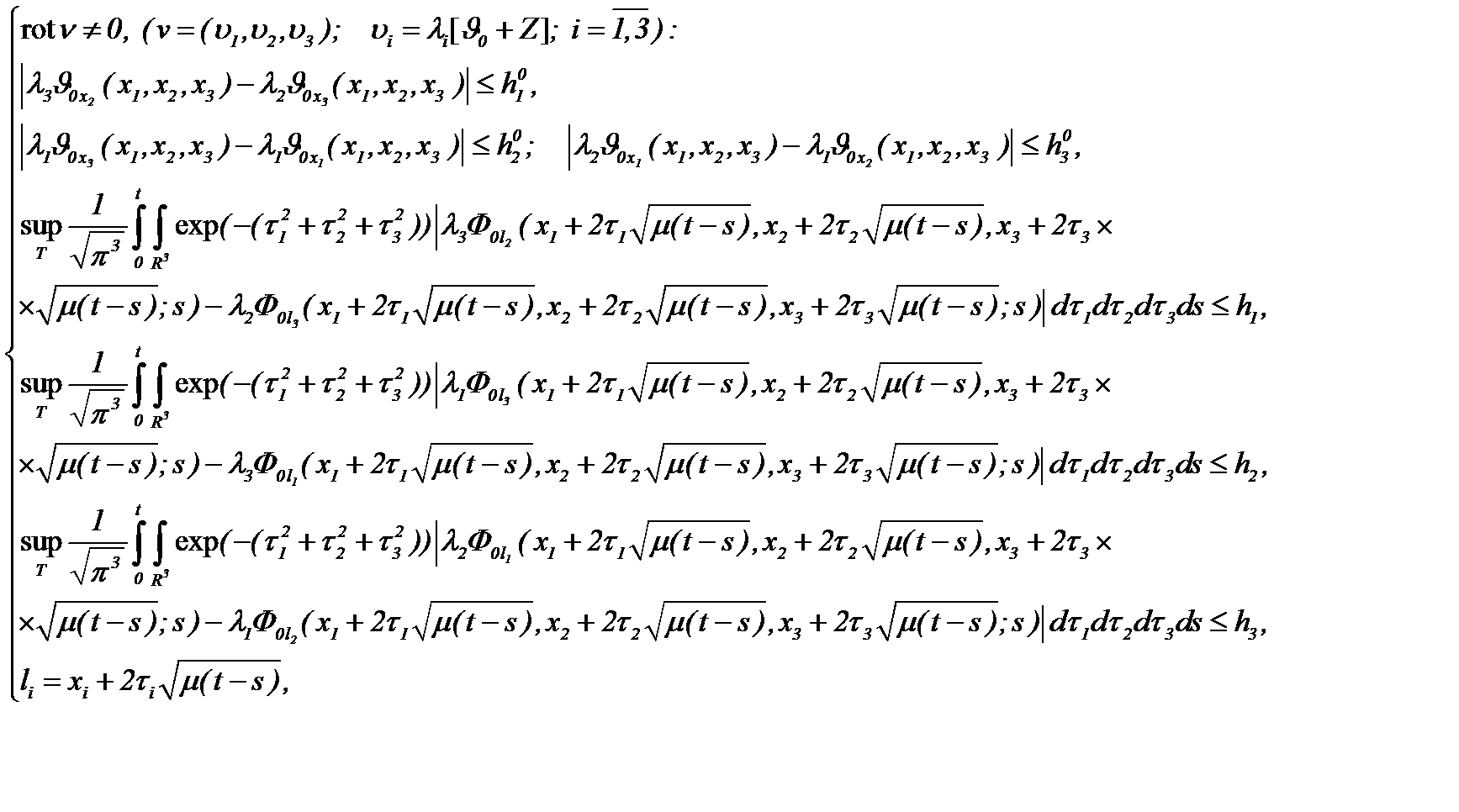
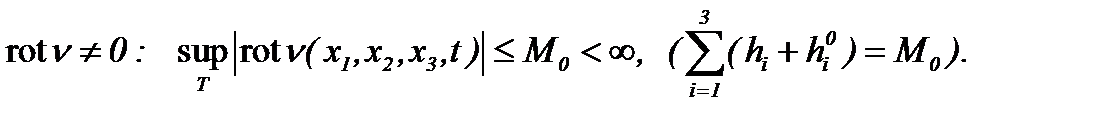 (4.19)
(4.19) 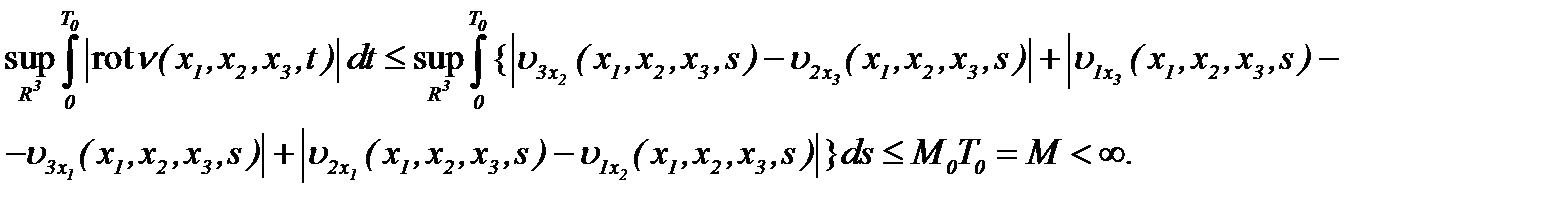 (4.20)
(4.20) 


