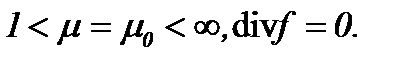В предыдущих параграфах исследованы различные варианты метода (4.12) для задачи Навье-Стокса в пространствах 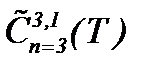 . Различными исследователями получена связь скорости и давления экспериментальными методами [12]. Например, у Бетца А., Джонса Б.M. и др. связь основана на соотношении типа Бернулли, поэтому скорости
. Различными исследователями получена связь скорости и давления экспериментальными методами [12]. Например, у Бетца А., Джонса Б.M. и др. связь основана на соотношении типа Бернулли, поэтому скорости 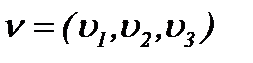 выражаются в конкретной форме. В нашем случае для решения 3D уравнений требуется ввести преобразования с помощью интегралов типа Пуассона, что позволит получить соотношение распределения давления, которое даст связь между давлением и скоростью в новой форме, а также позволит выразить скорость в интегральной форме.
выражаются в конкретной форме. В нашем случае для решения 3D уравнений требуется ввести преобразования с помощью интегралов типа Пуассона, что позволит получить соотношение распределения давления, которое даст связь между давлением и скоростью в новой форме, а также позволит выразить скорость в интегральной форме.
В этой связи, в данном пункте рассматривается метод комплексного преобразования на основе интегралов Пуассона, когда 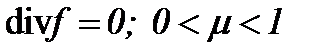 или
или 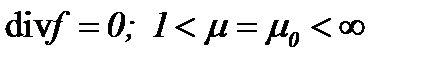 . Поэтому на основе разработанного метода система Навье-Стокса (1.1) с условиями (1.2) и (1.3) может иметь гладкое единственное решение в
. Поэтому на основе разработанного метода система Навье-Стокса (1.1) с условиями (1.2) и (1.3) может иметь гладкое единственное решение в 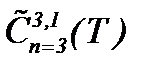 , причем в аналитической форме, что и выясним.
, причем в аналитической форме, что и выясним.
6.1. Жидкость с очень малой вязкостью 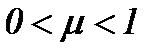 , когда
, когда 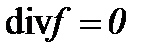
I . Для несжимаемых течений с трением, если
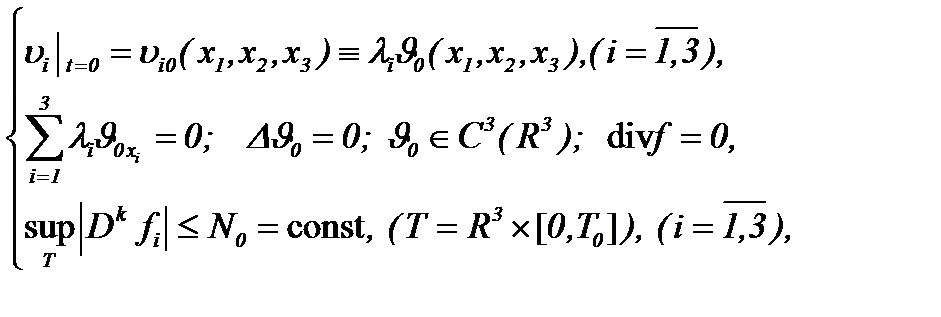 (6.1)
(6.1)
то функции 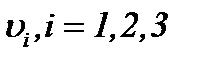 представимы в виде
представимы в виде
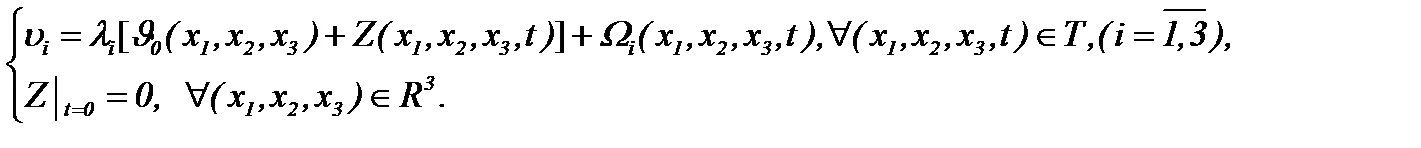 (6.2)
(6.2)
От введенных функций 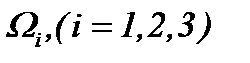 требуется, чтобы
требуется, чтобы
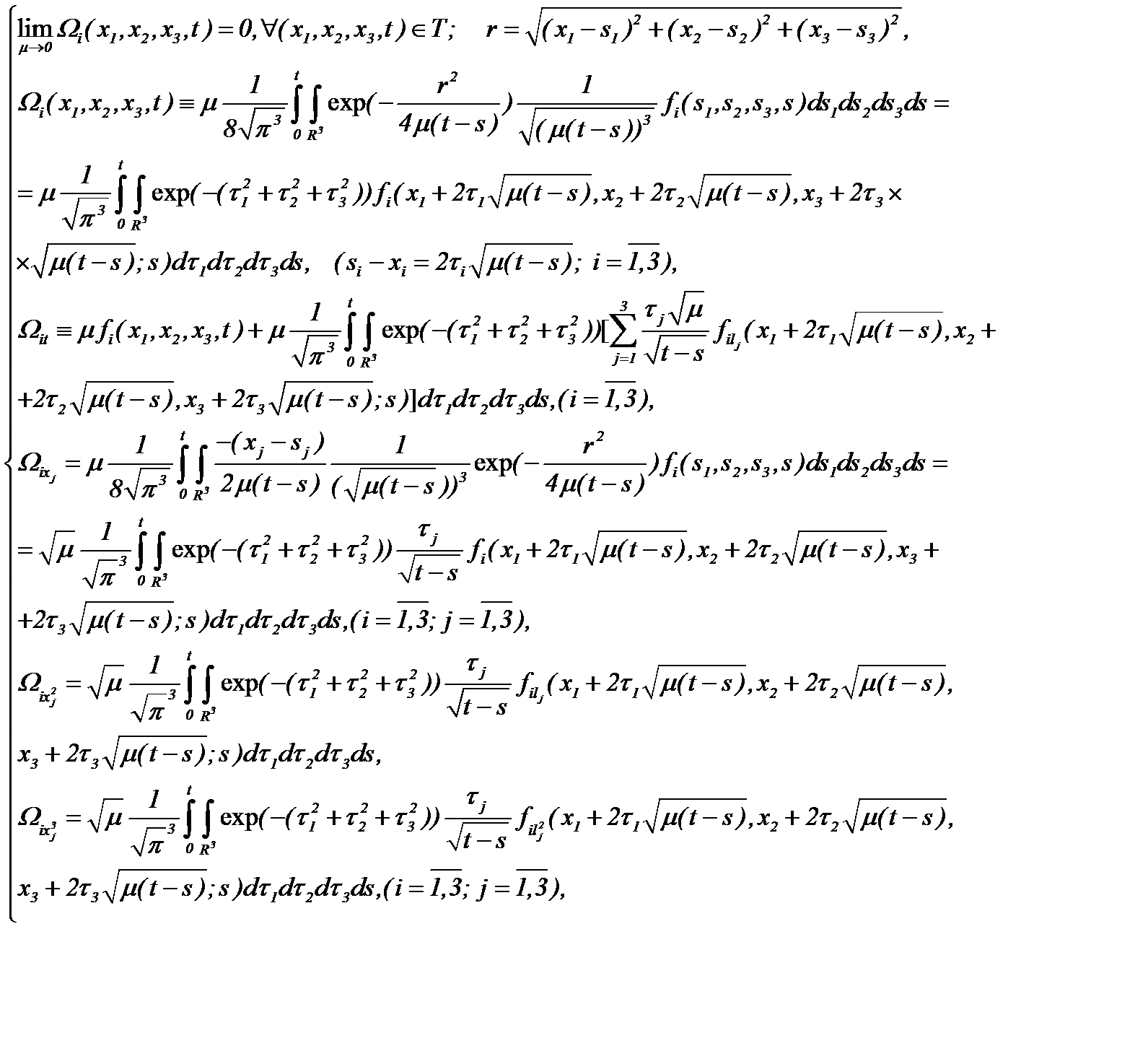
где 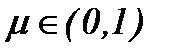 выступает в роли малого параметра, причем
выступает в роли малого параметра, причем
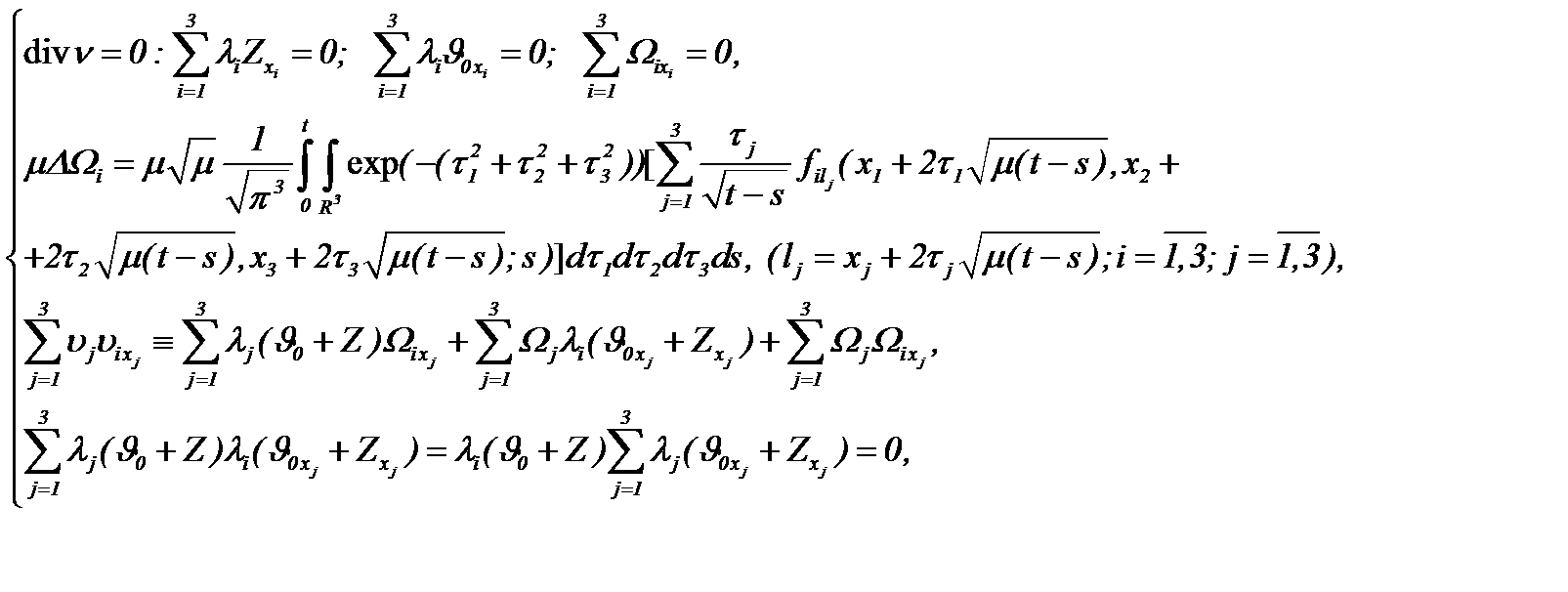
 (6.3)
(6.3)
Тогда уравнения Навье-Стокса (1.1) для несжимаемых течений с трением трансформируются с помощью (6.1) – (6.3) и принимают следующий вид
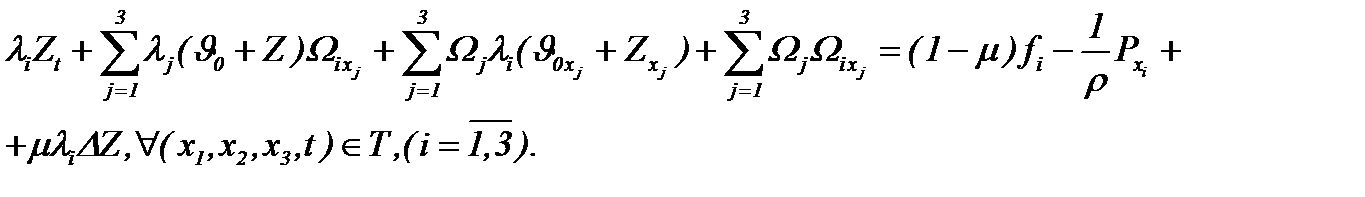 (6.4)
(6.4)
Из системы (6.4), учитывая условия (6.1) – (6.3) и применяя АПС, получаем
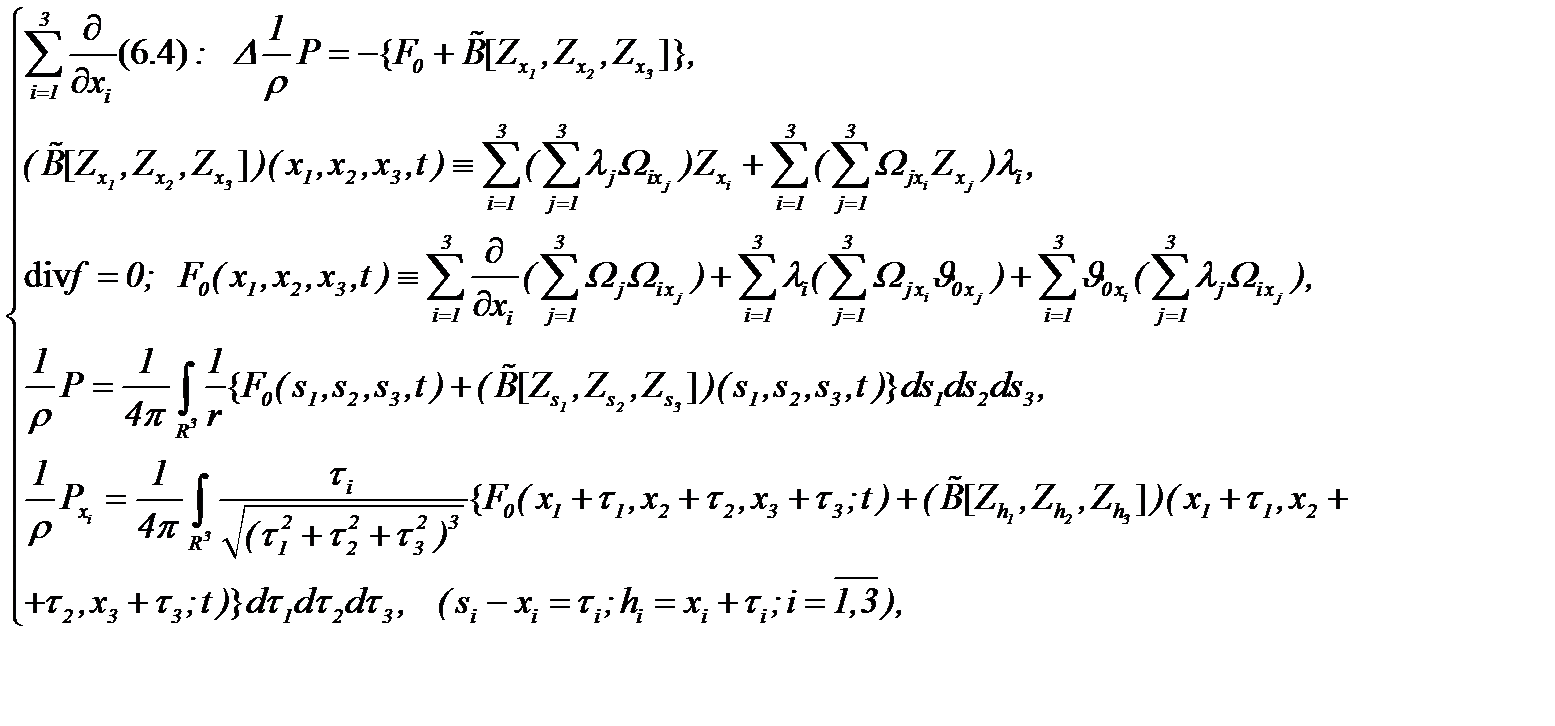 (6.5)
(6.5)
так как выполняются условия
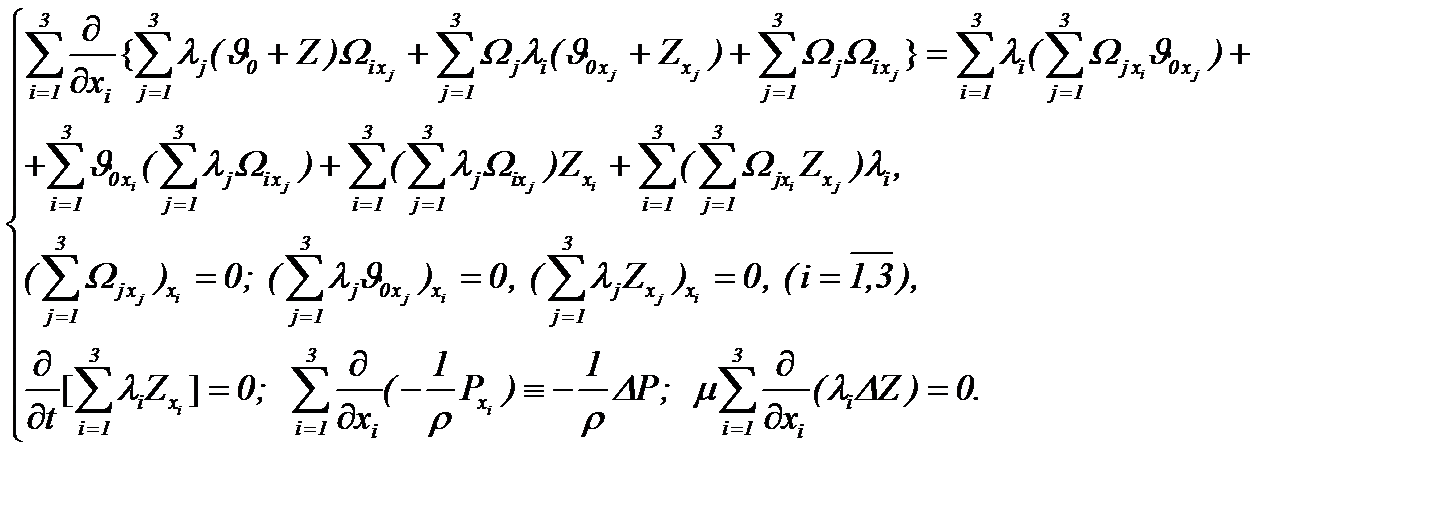
Поэтому, на основе выражения (6.5) система (6.4) эквивалентно преобразуется к виду
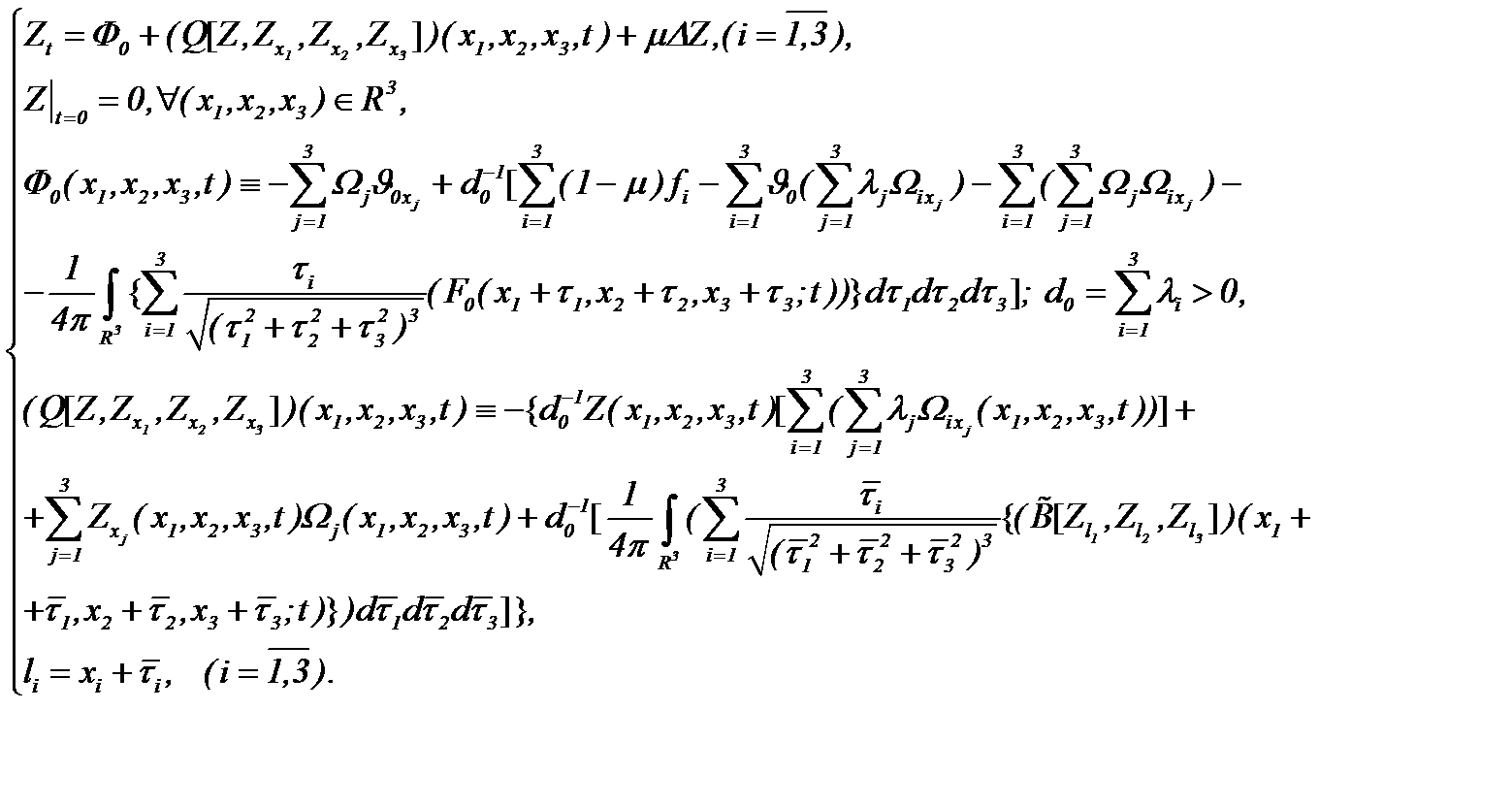 (6.6)
(6.6)
Значит, задача (6.6) сводится к системе интегральных уравнений, вполне регулярных относительно параметра вязкости 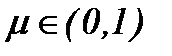
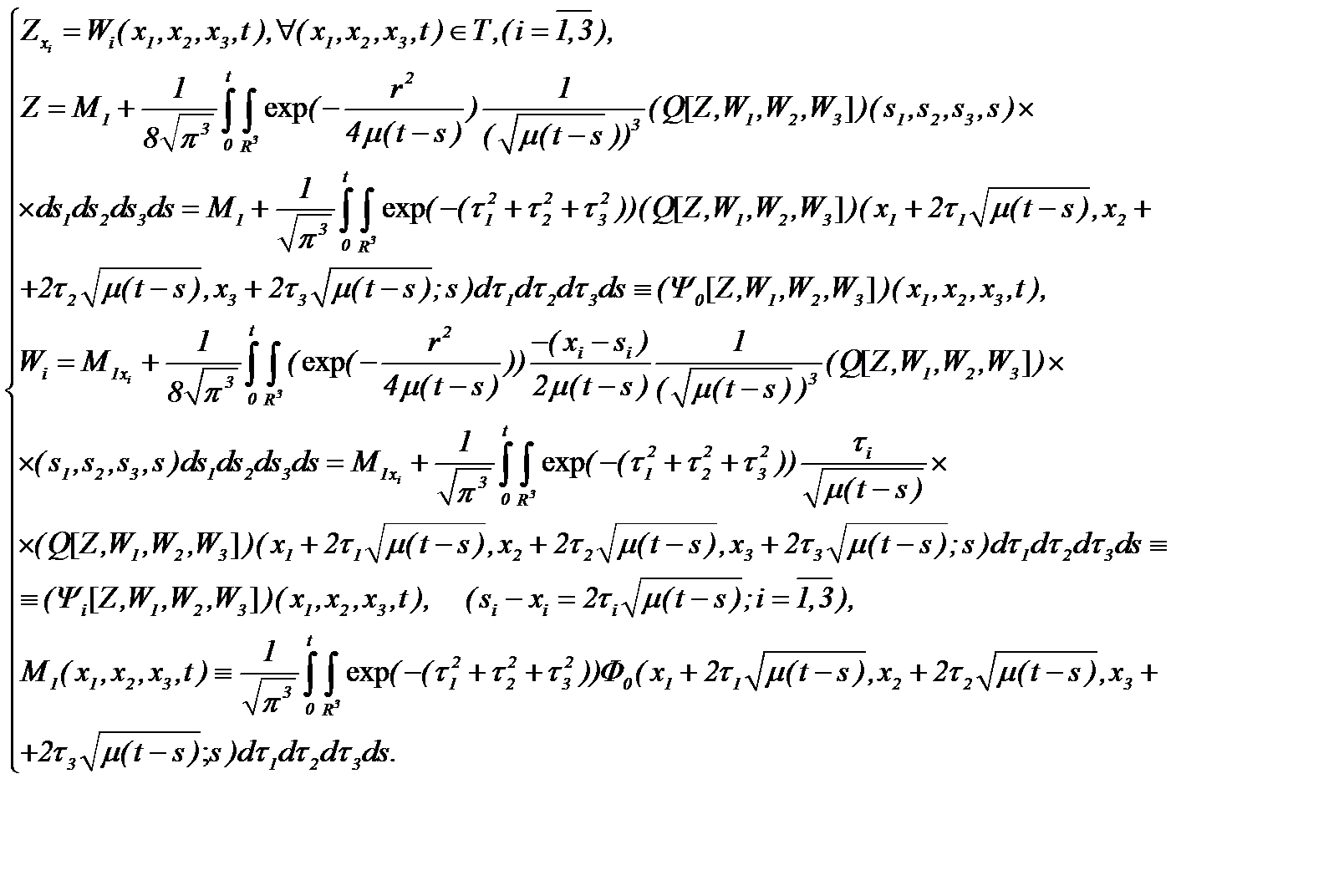 (6.7)
(6.7)
Пусть известные функции 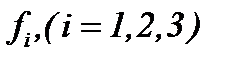 являются субмультипликативными функциями [15] и имеет место
являются субмультипликативными функциями [15] и имеет место
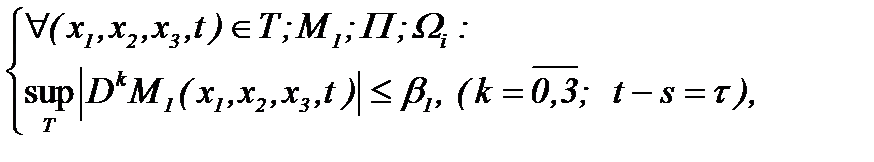
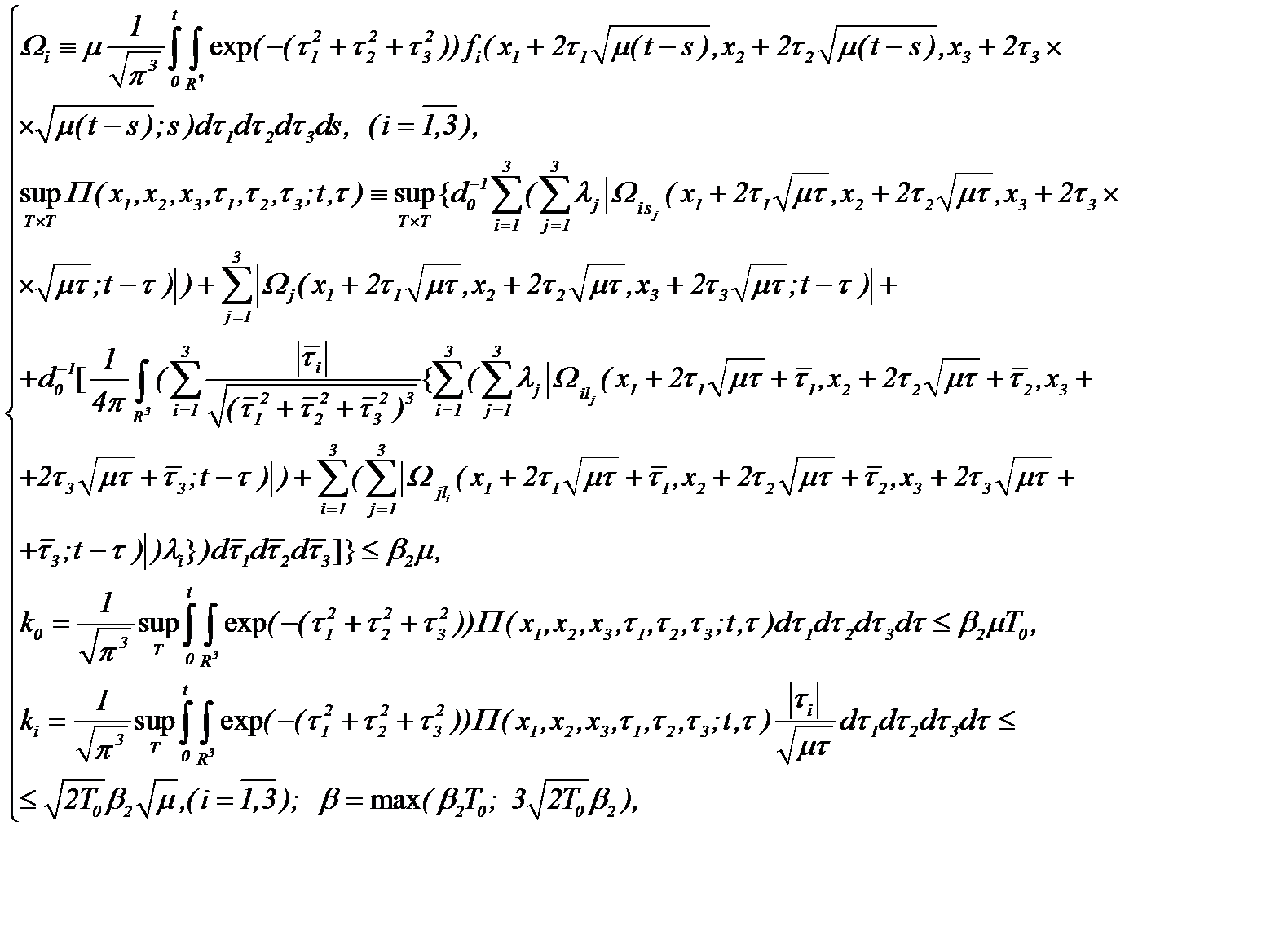 (6.8)
(6.8)
причем операторы  допускают условия принципа сжимающих отображений:
допускают условия принципа сжимающих отображений:
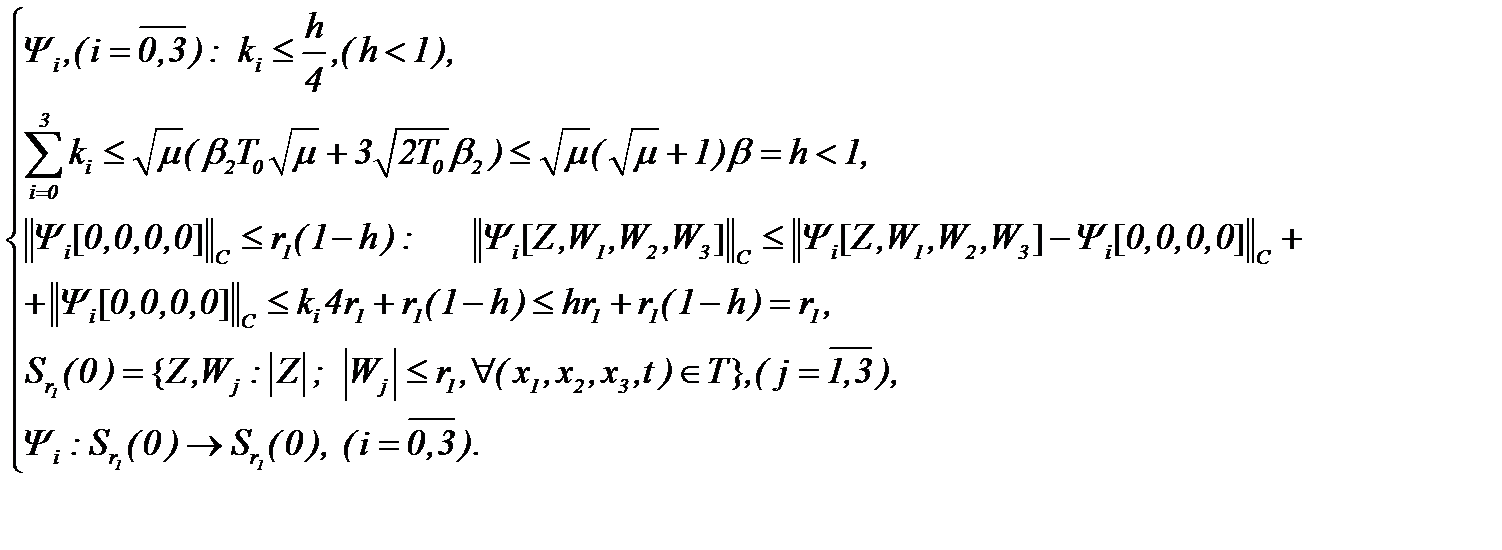 (6.9)
(6.9)
Тогда система (6.7) однозначно разрешима, а решение этой системы можем найти на основе метода Пикара
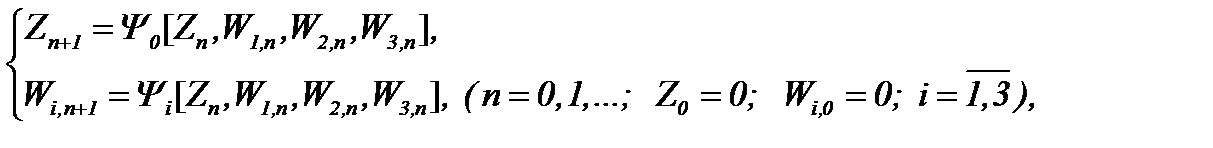 (6.10)
(6.10)
при этом имеет место
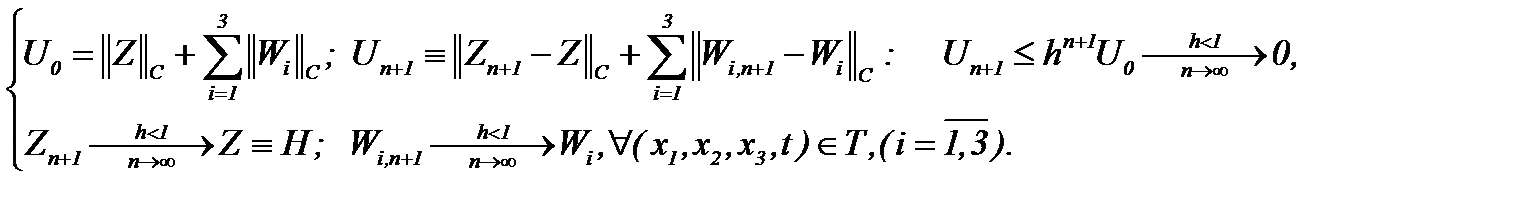 (6.11)
(6.11)
Поэтому на основании (6.2) и
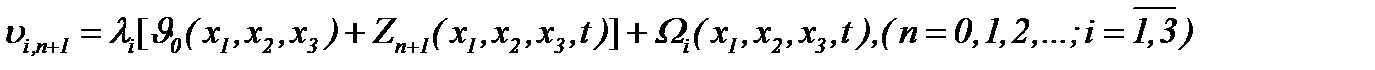 (6.12)
(6.12)
получим
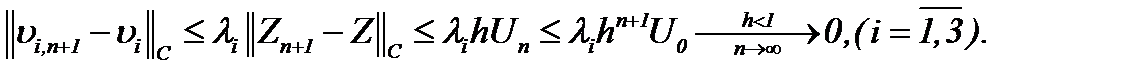 (6.13)
(6.13)
Это значит, что последовательность 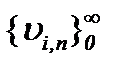 сходится к пределу
сходится к пределу 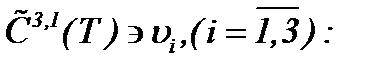
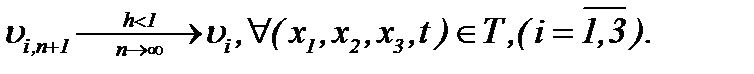 (6.14)
(6.14)
А потому задача Навье-Стокса при условиях (1.2), (6.1), (6.2), (6.8), (6.9) и (6.14) имеет гладкое единственное решение вида (6.2) в 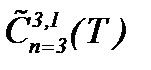 .
.
Жидкость с вязкостью, когда div f = 0
6.2. Жидкость с вязкостью 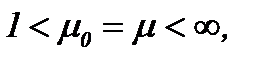 когда
когда 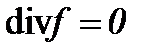
В параграфе 5 были исследованы уравнения Навье-Стокса с вязкостью среднего размера, при этом введенные математические преобразования свели нелинейные члены конвективного ускорения к линейному виду. Тем самым, с помощью новой теории получены неоднородные линейные уравнения теплопроводности с условием Коши.
Для развития предлагаемой теории рассмотрим аналогичные задачи для жидкости с небольшим числом Рейнольдса и со всеми членами конвективного ускорения в уравнениях Навье-Стокса. В отличие от параграфа 5 будем рассматривать методы интегральных преобразований на основе интегралов типа Пуассона в 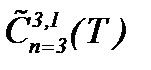 , когда
, когда 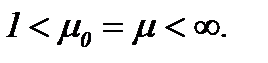 Метод аналитического решения уравнений Навье-Стокса, который дает интегрируемость этих уравнений, применяется в случае
Метод аналитического решения уравнений Навье-Стокса, который дает интегрируемость этих уравнений, применяется в случае
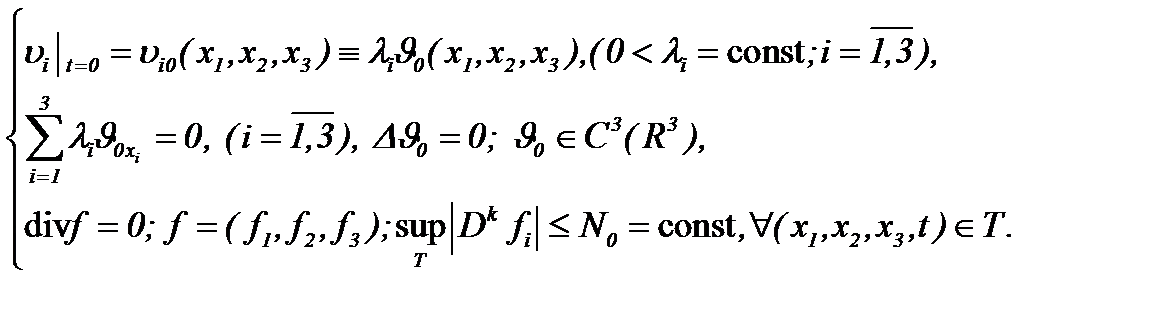 (6.15)
(6.15)
На основании чего, вводим формулу для определения компонент скоростей:
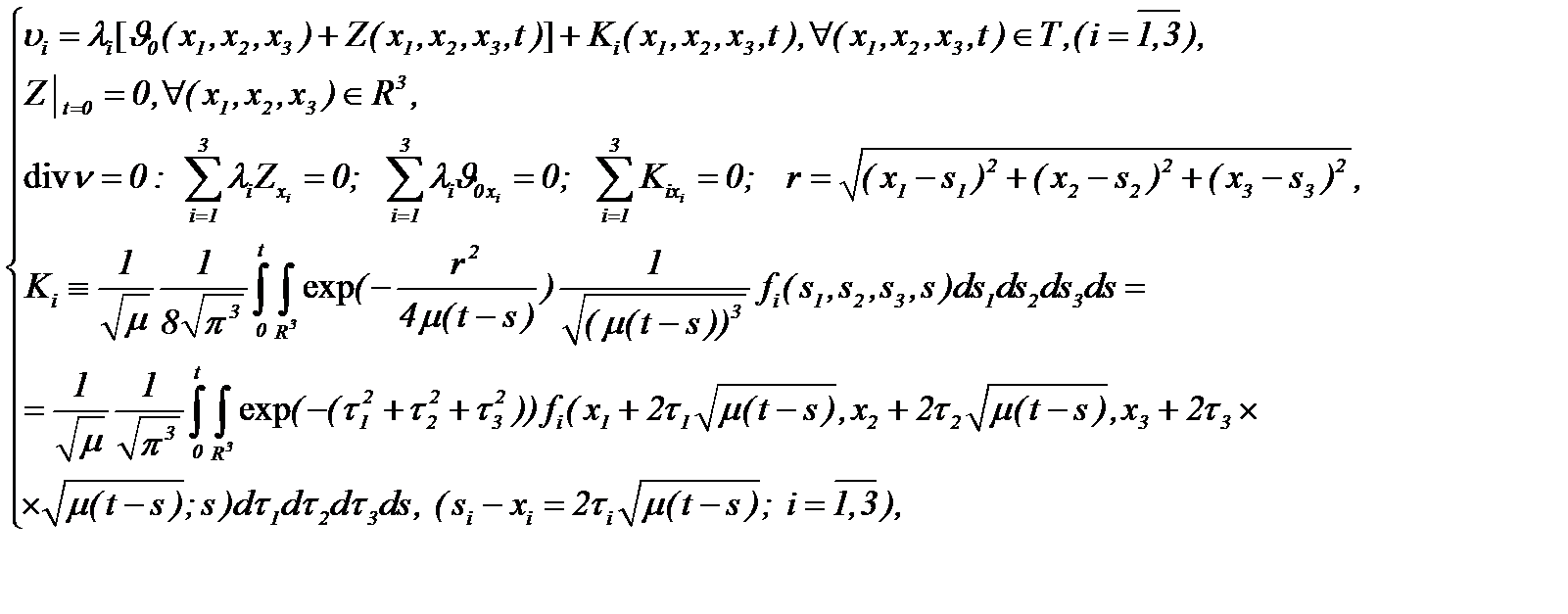 (6.16)
(6.16)
причем
 (6.17)
(6.17)
Следовательно, с помощью (6.15) – (6.17) система Навье-Стокса (1.1) сводится к виду
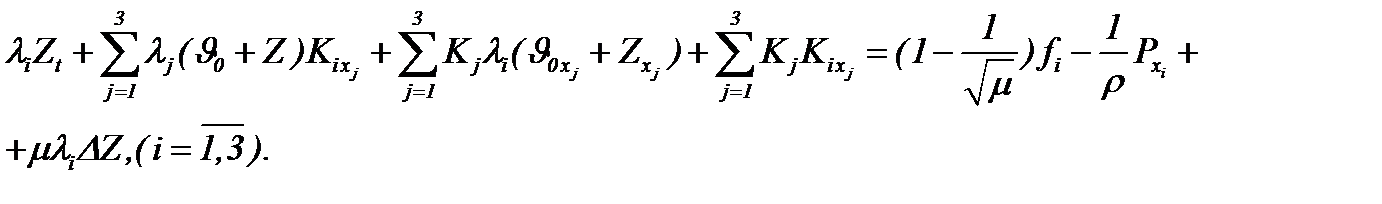 (6.18)
(6.18)
Поэтому из системы (6.18) с учетом (6.5) – (6.7), где вместо 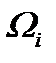 рассматриваем
рассматриваем 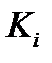 , получим
, получим
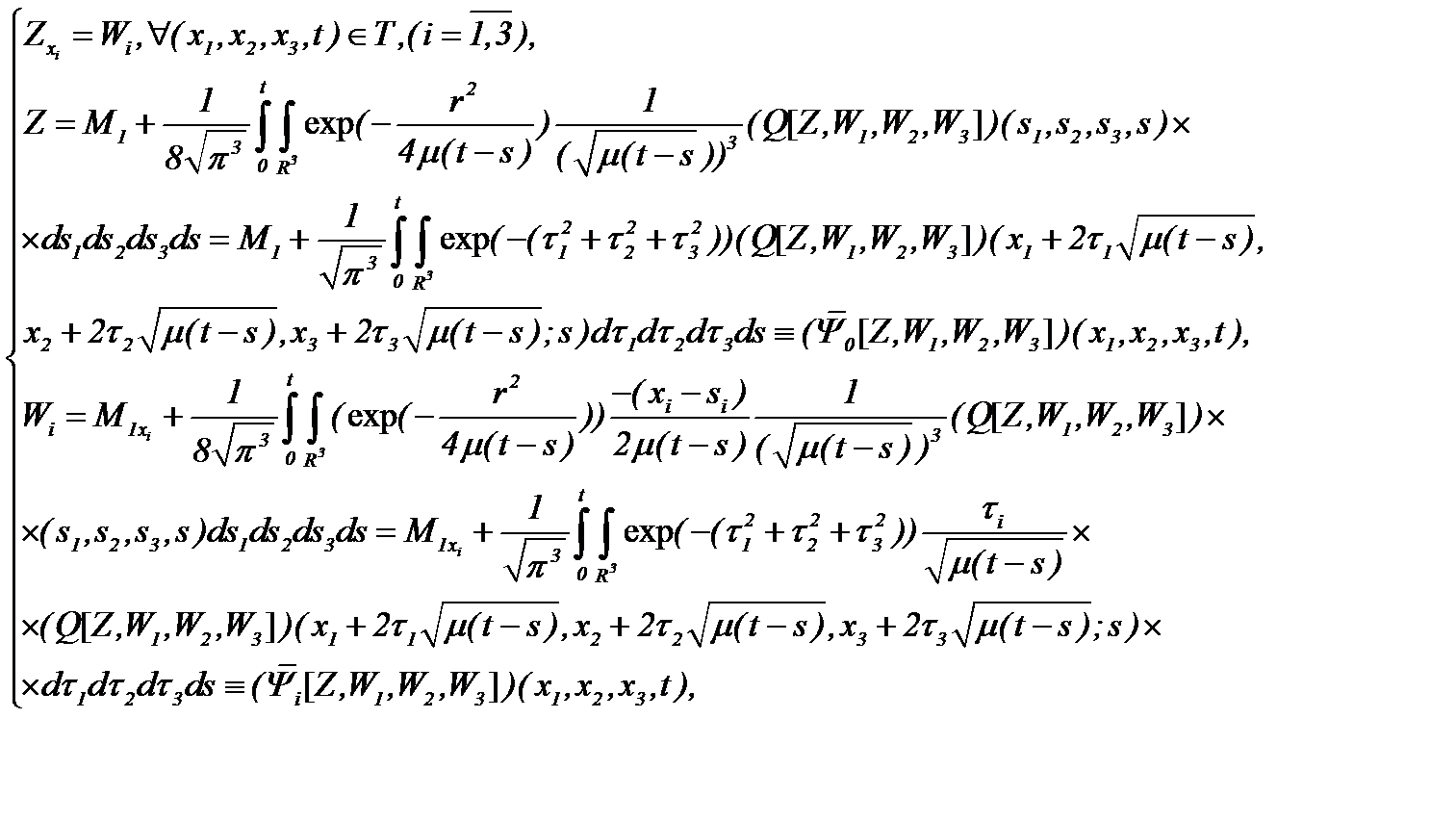 (6.19)
(6.19)
в которых
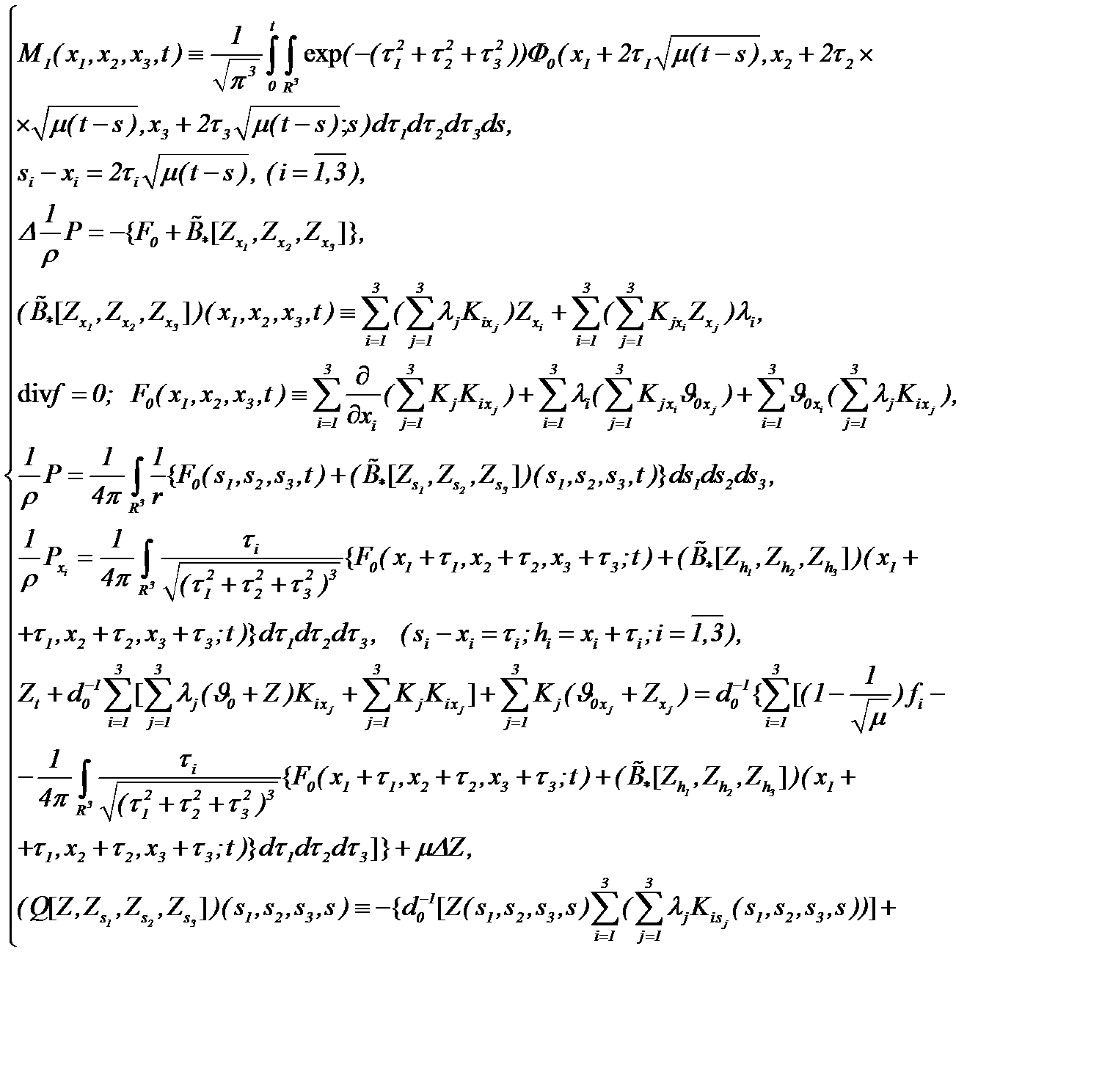
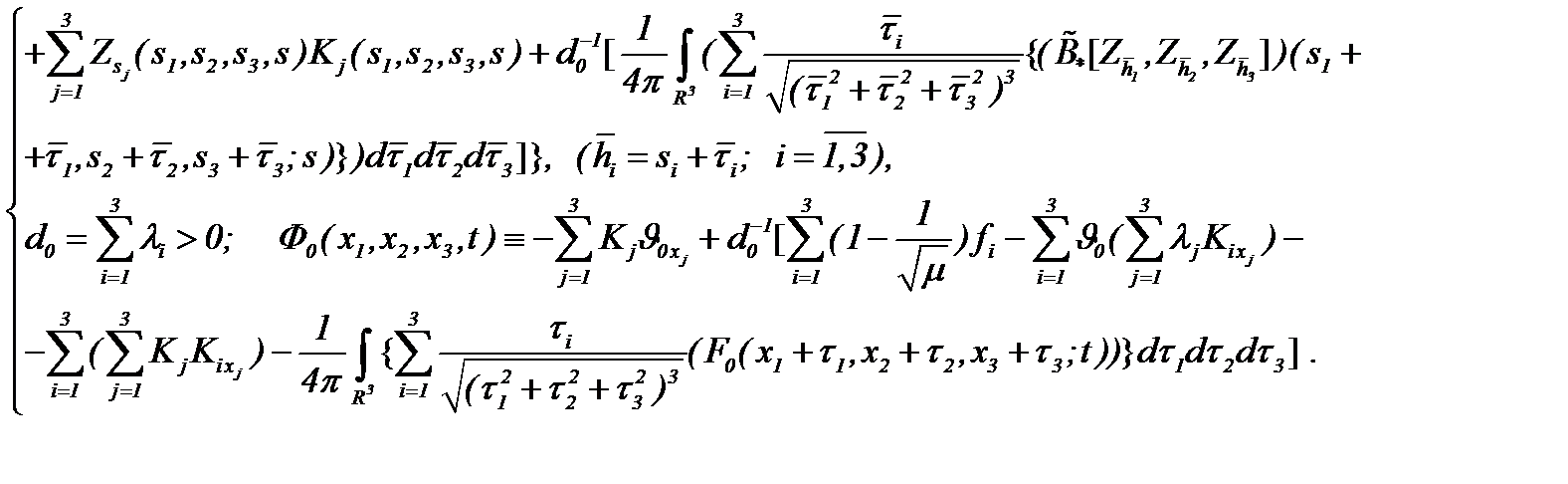
Если имеет место
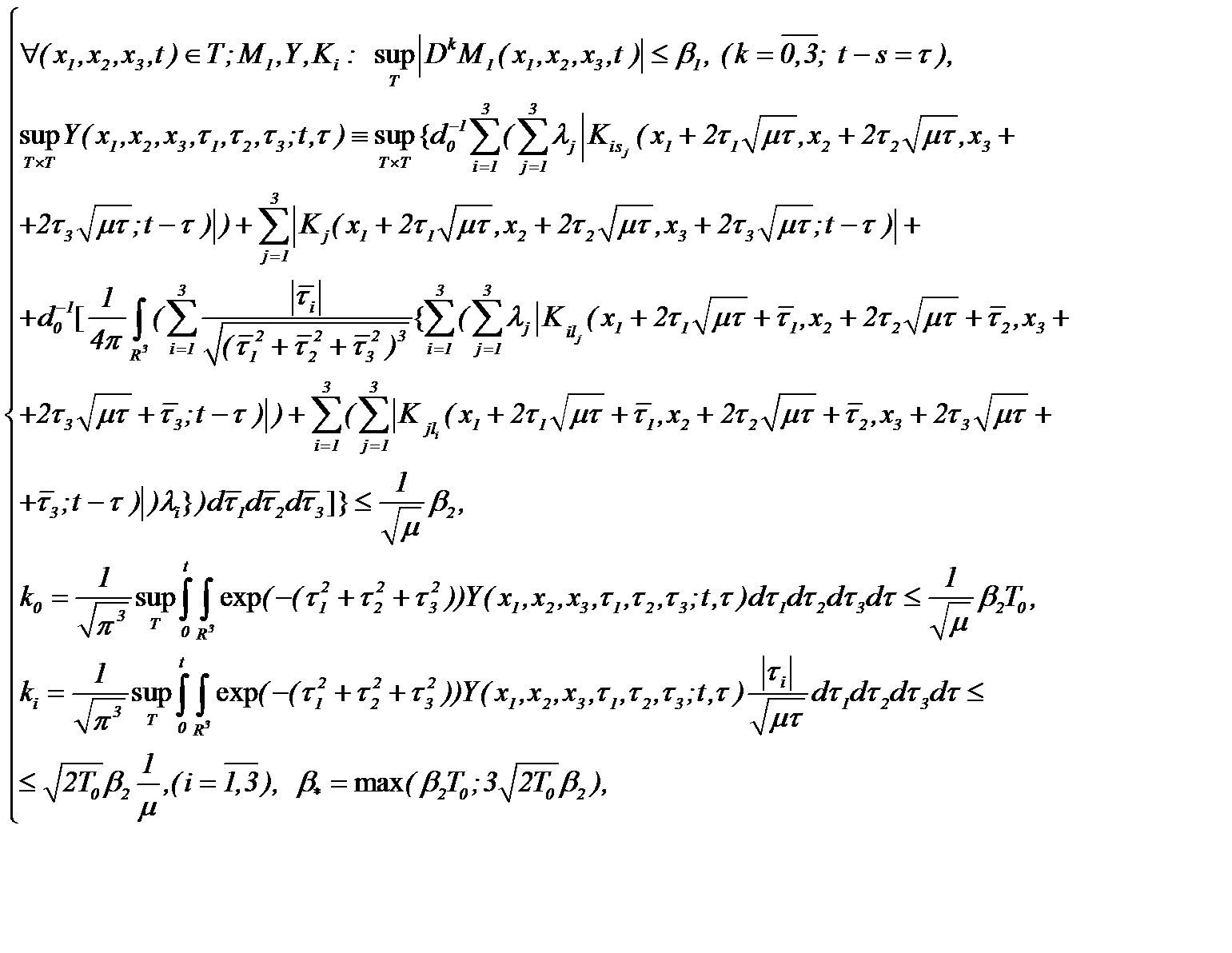 (6.20)
(6.20)
а операторы 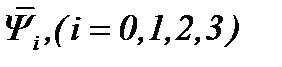 допускают условия
допускают условия
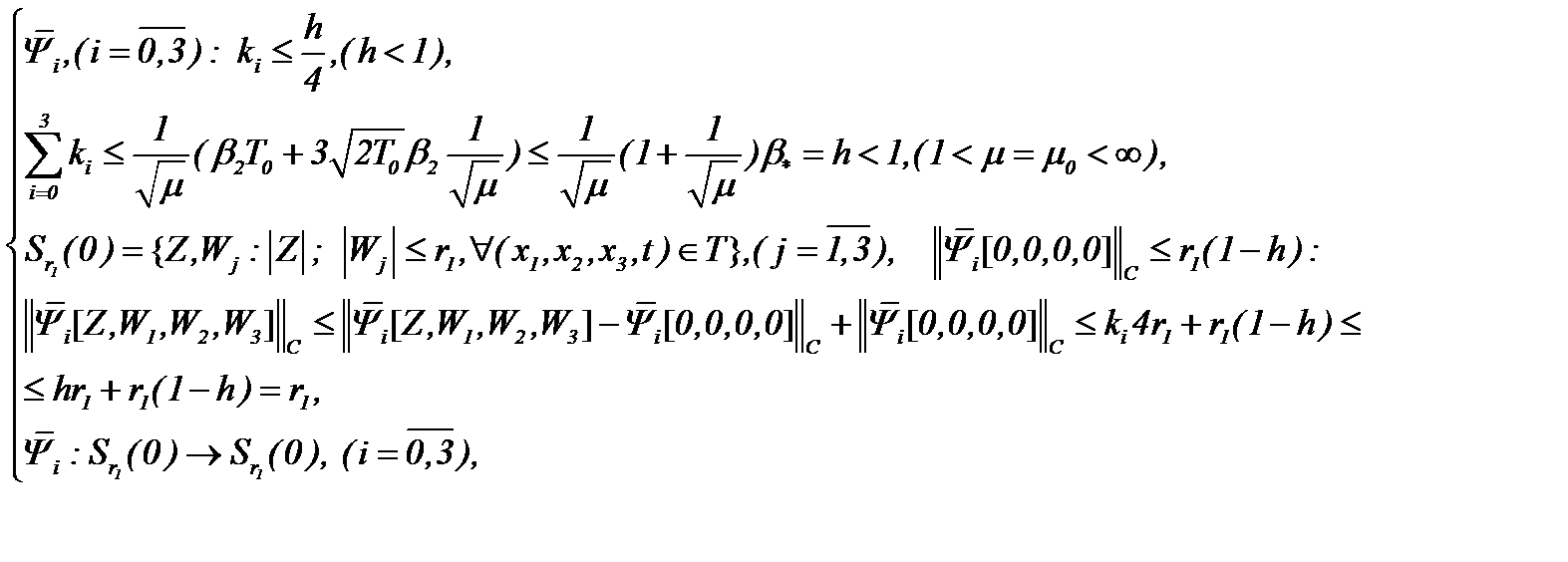 (6.21)
(6.21)
то относительно этих операторов выполняются условия сжимающих отображений. Это означает, что система (6.19) однозначно разрешима, а решение данной системы определяется по методу Пикара (6.10). Тогда с учетом результатов (6.11) – (6.14) получим, что последовательности функций 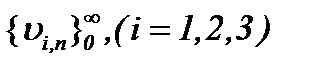 сходятся к пределу
сходятся к пределу 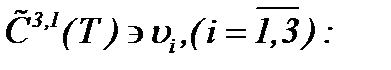
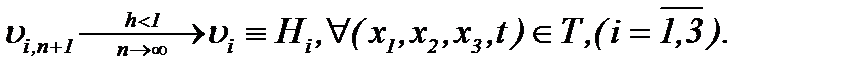 (6.22)
(6.22)
Как следствие пунктов 6.1 и 6.2, получим следующие утверждения.
Теорема 7. Нестационарная задача Навье-Стокса (1.1) – (1.3) разрешима в 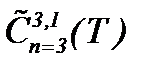 , когда
, когда
выполнены условия:
a ) (6.1), (6.2), (6.8), (6.9), (6.14) и 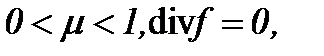 или
или
б) (6.15) – (6.17), (6.20), (6.21), (6.22) и 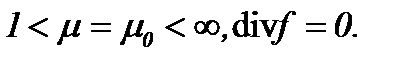





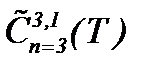 . Различными исследователями получена связь скорости и давления экспериментальными методами [12]. Например, у Бетца А., Джонса Б.M. и др. связь основана на соотношении типа Бернулли, поэтому скорости
. Различными исследователями получена связь скорости и давления экспериментальными методами [12]. Например, у Бетца А., Джонса Б.M. и др. связь основана на соотношении типа Бернулли, поэтому скорости 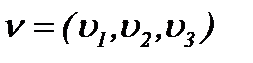 выражаются в конкретной форме. В нашем случае для решения 3D уравнений требуется ввести преобразования с помощью интегралов типа Пуассона, что позволит получить соотношение распределения давления, которое даст связь между давлением и скоростью в новой форме, а также позволит выразить скорость в интегральной форме.
выражаются в конкретной форме. В нашем случае для решения 3D уравнений требуется ввести преобразования с помощью интегралов типа Пуассона, что позволит получить соотношение распределения давления, которое даст связь между давлением и скоростью в новой форме, а также позволит выразить скорость в интегральной форме.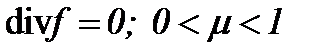 или
или 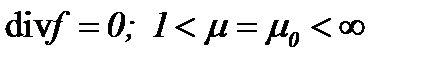 . Поэтому на основе разработанного метода система Навье-Стокса (1.1) с условиями (1.2) и (1.3) может иметь гладкое единственное решение в
. Поэтому на основе разработанного метода система Навье-Стокса (1.1) с условиями (1.2) и (1.3) может иметь гладкое единственное решение в 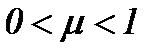 , когда
, когда 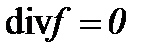
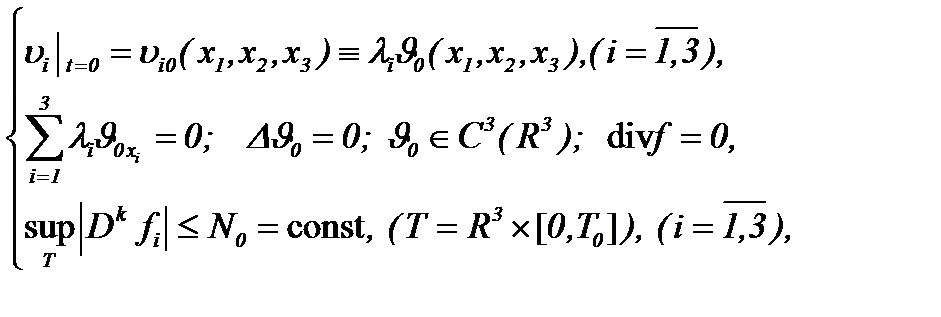 (6.1)
(6.1) 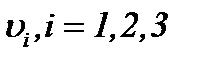 представимы в виде
представимы в виде 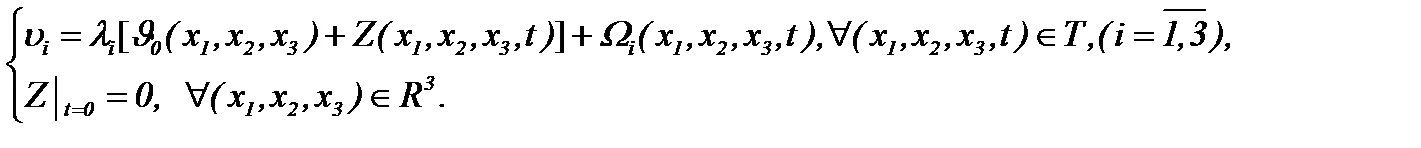 (6.2)
(6.2)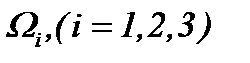 требуется, чтобы
требуется, чтобы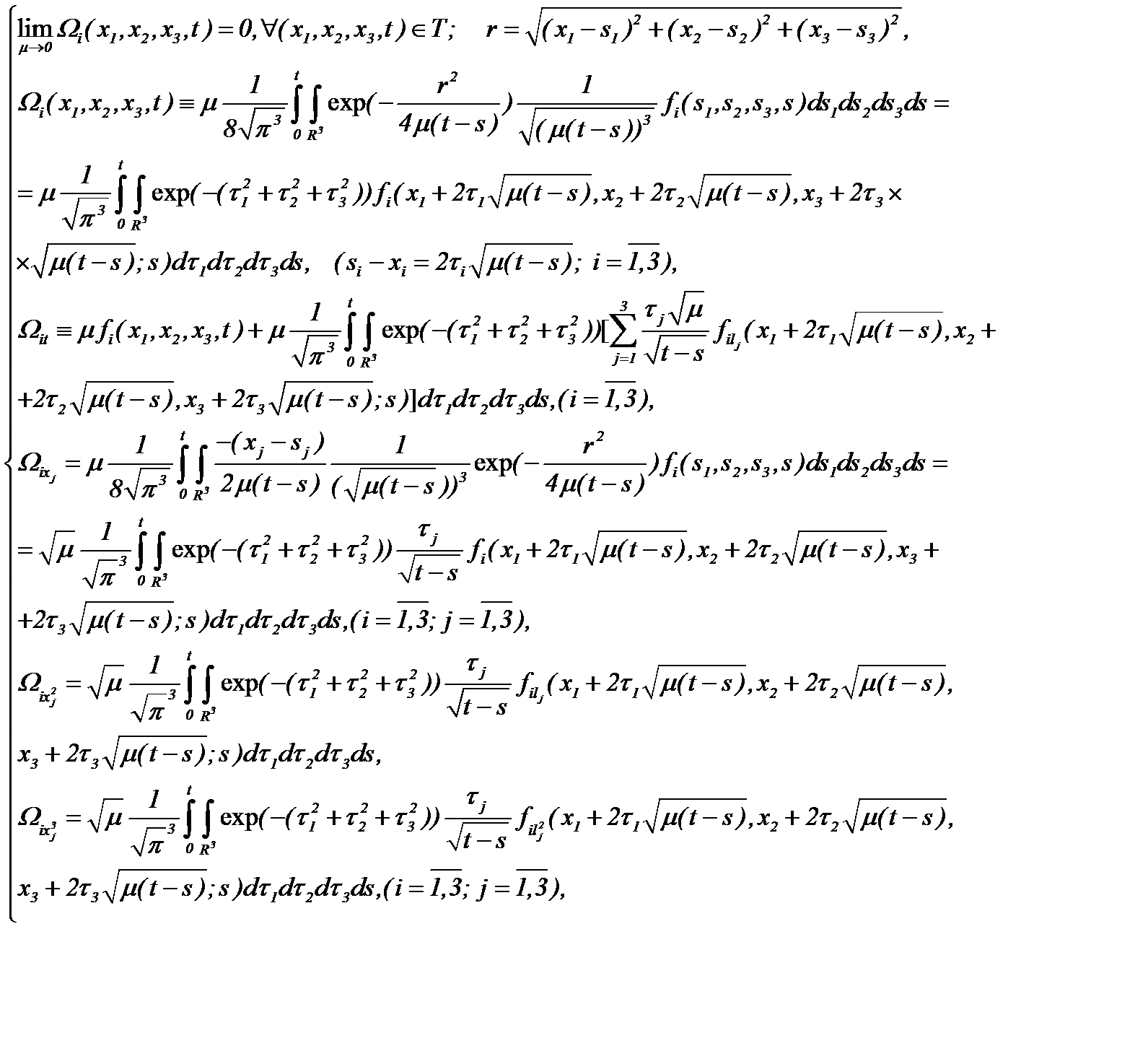
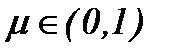 выступает в роли малого параметра, причем
выступает в роли малого параметра, причем 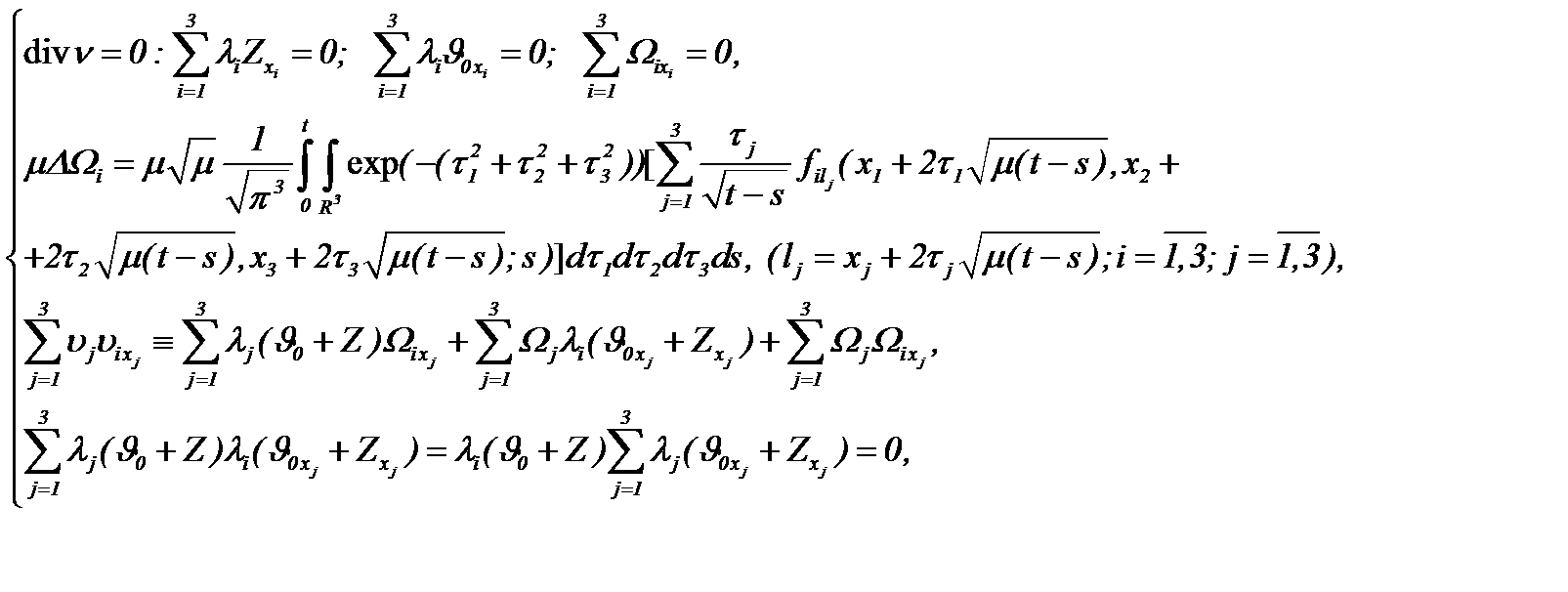
 (6.3)
(6.3)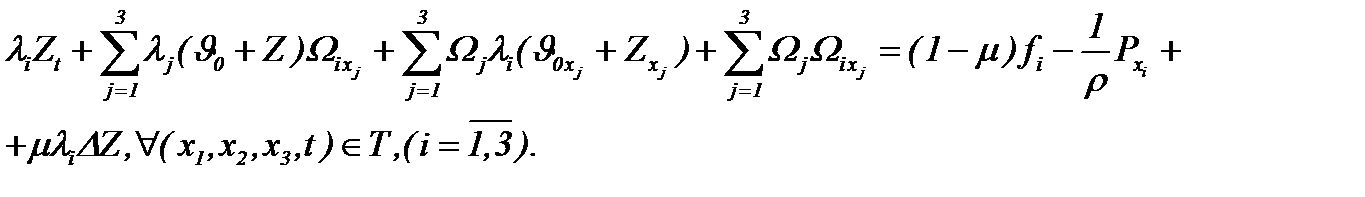 (6.4)
(6.4)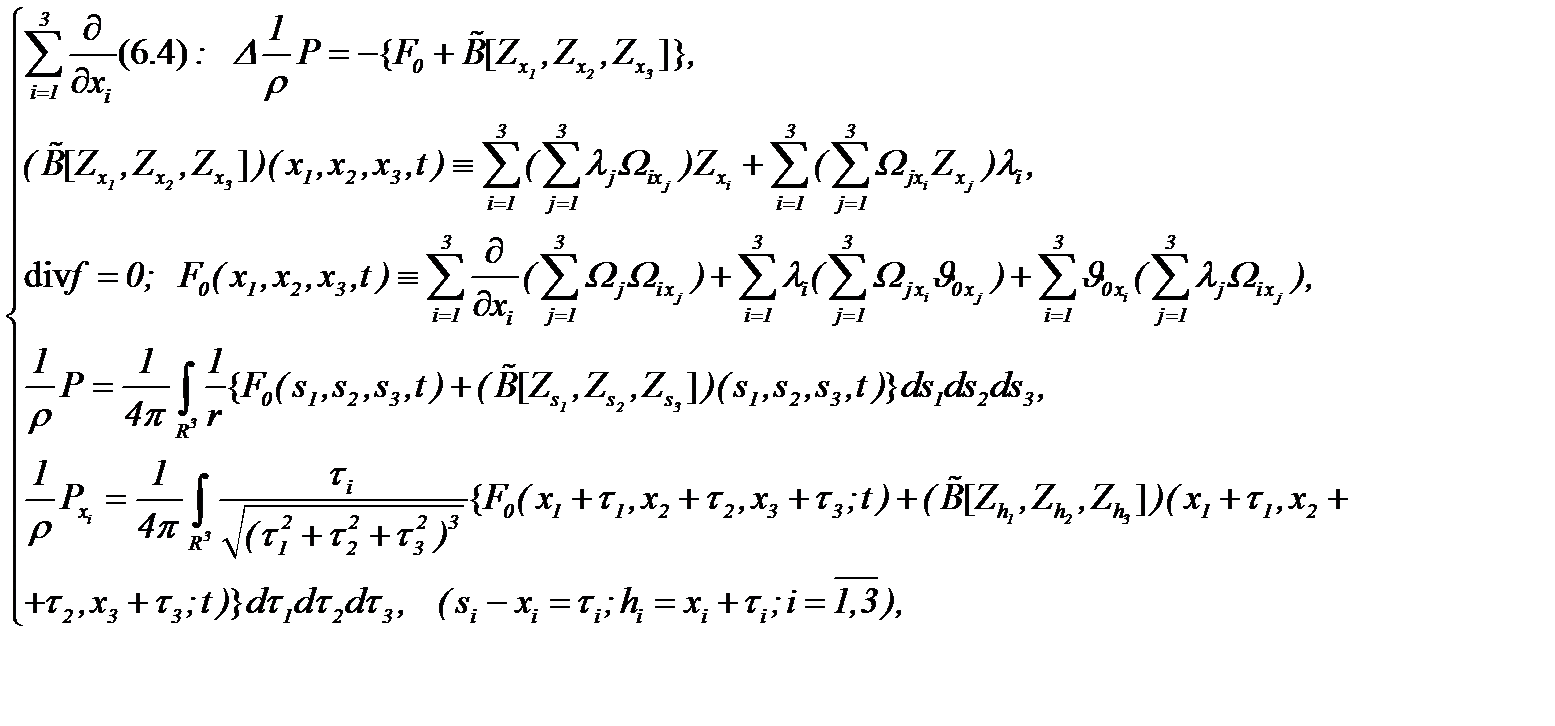 (6.5)
(6.5)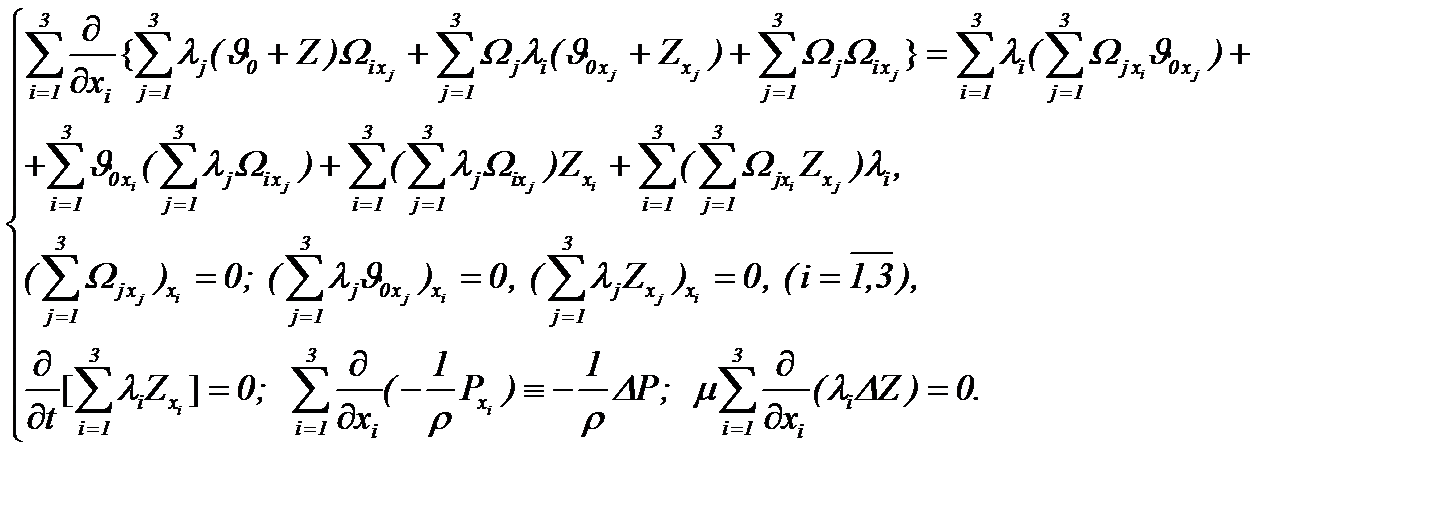
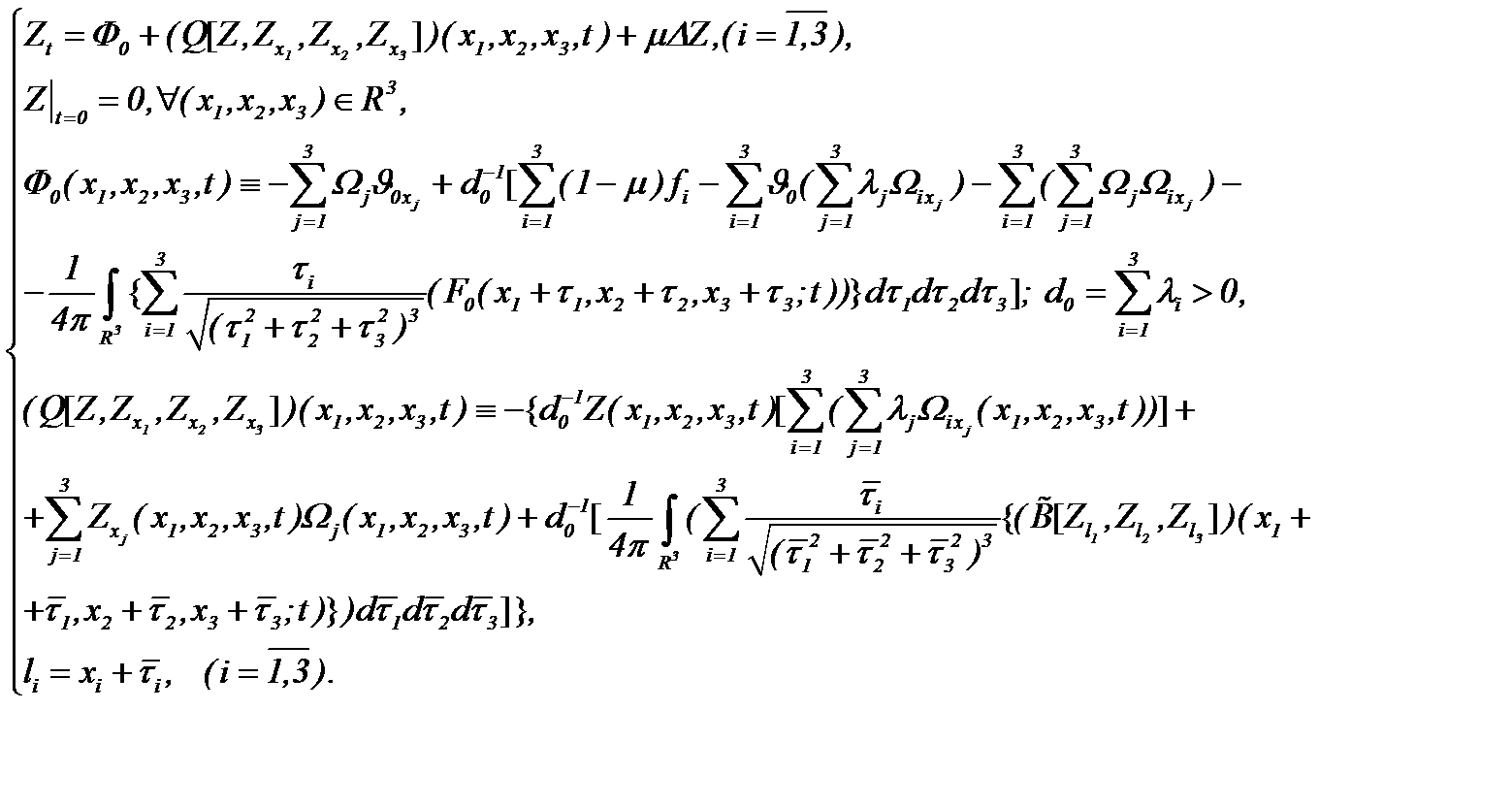 (6.6)
(6.6)
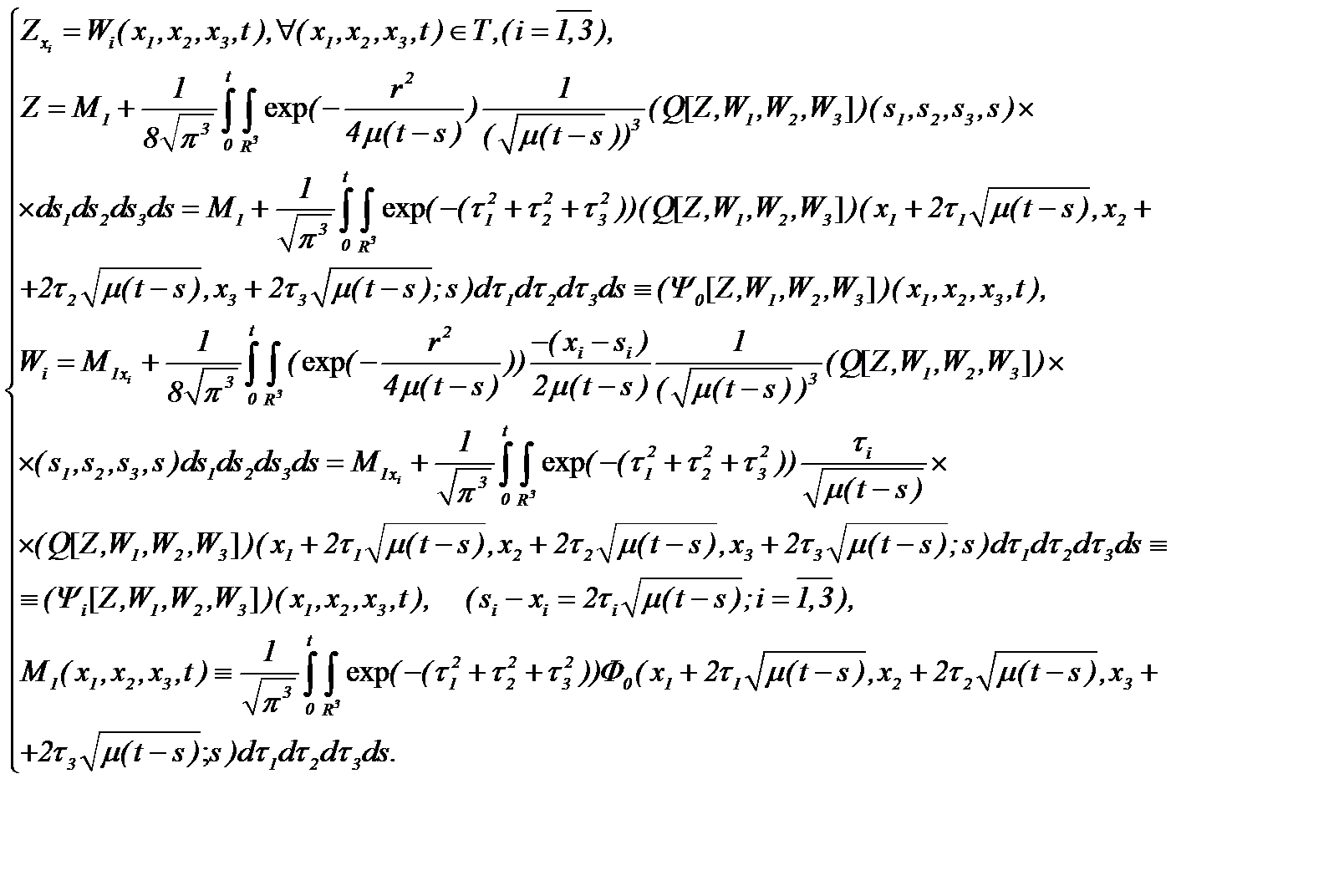 (6.7)
(6.7)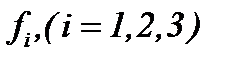 являются субмультипликативными функциями [15] и имеет место
являются субмультипликативными функциями [15] и имеет место 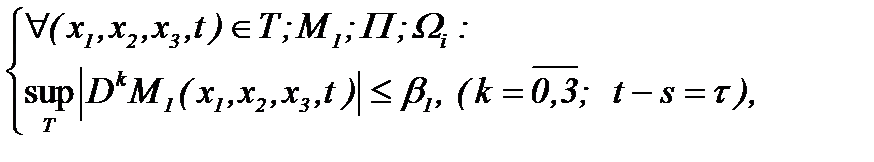
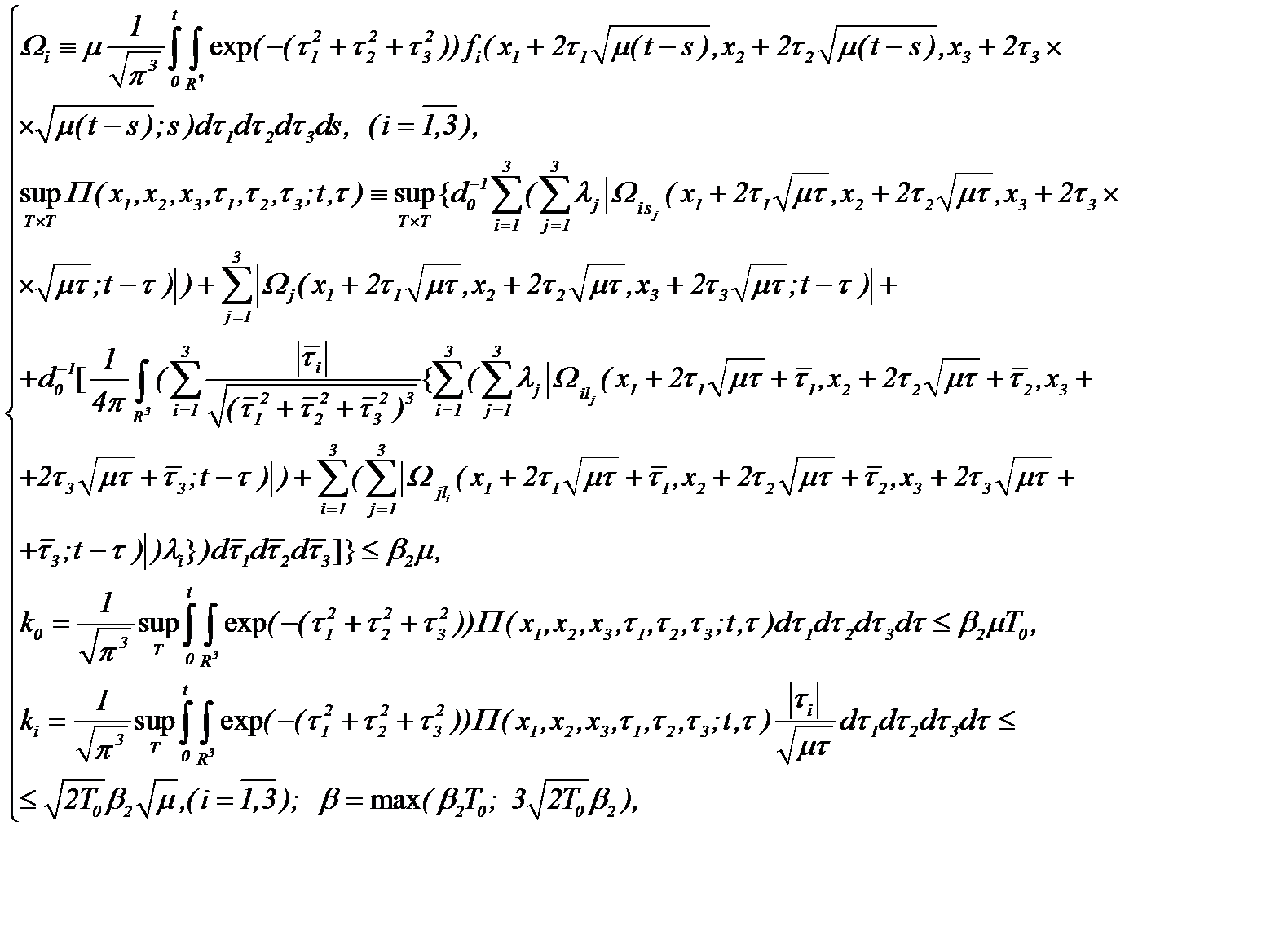 (6.8)
(6.8) допускают условия принципа сжимающих отображений:
допускают условия принципа сжимающих отображений: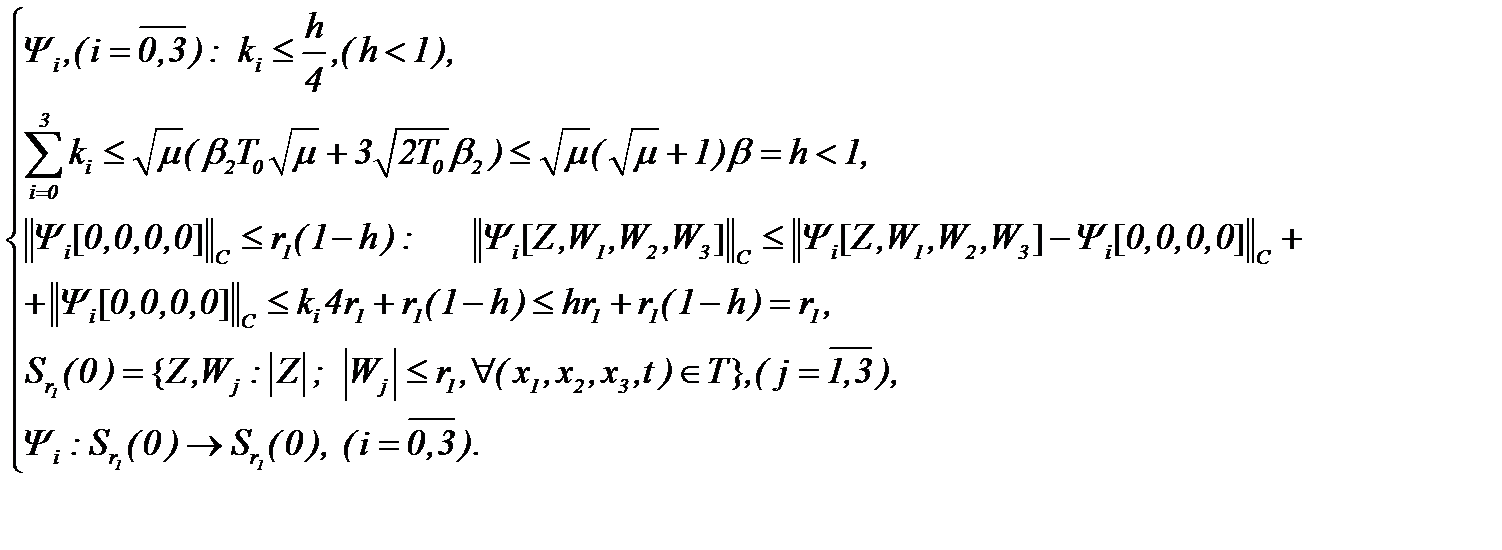 (6.9)
(6.9)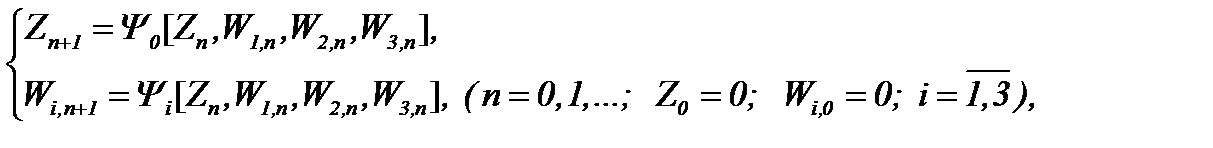 (6.10)
(6.10)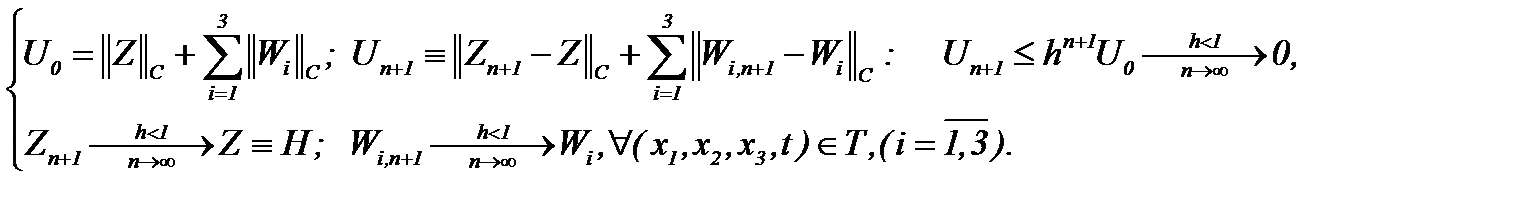 (6.11)
(6.11)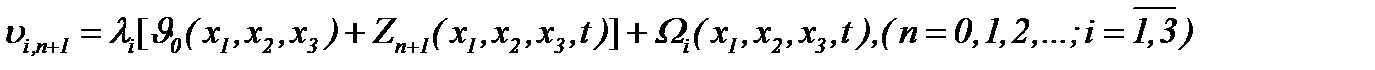 (6.12)
(6.12)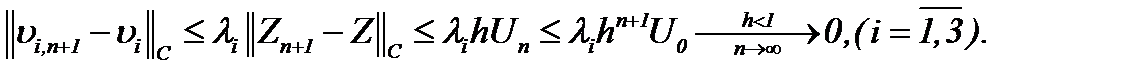 (6.13)
(6.13)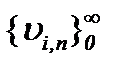 сходится к пределу
сходится к пределу 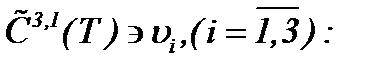
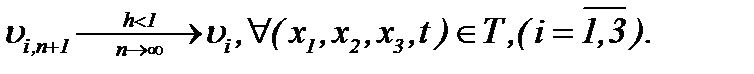 (6.14)
(6.14)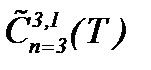 .
.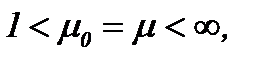 когда
когда 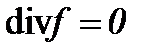
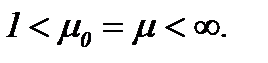 Метод аналитического решения уравнений Навье-Стокса, который дает интегрируемость этих уравнений, применяется в случае
Метод аналитического решения уравнений Навье-Стокса, который дает интегрируемость этих уравнений, применяется в случае 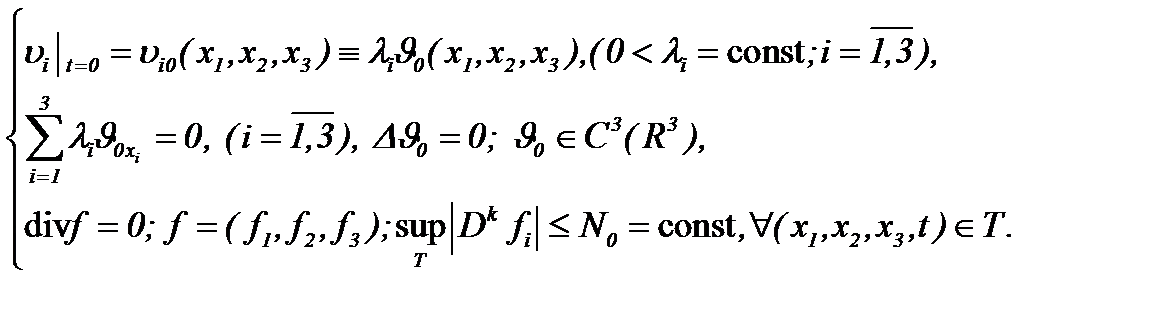 (6.15)
(6.15)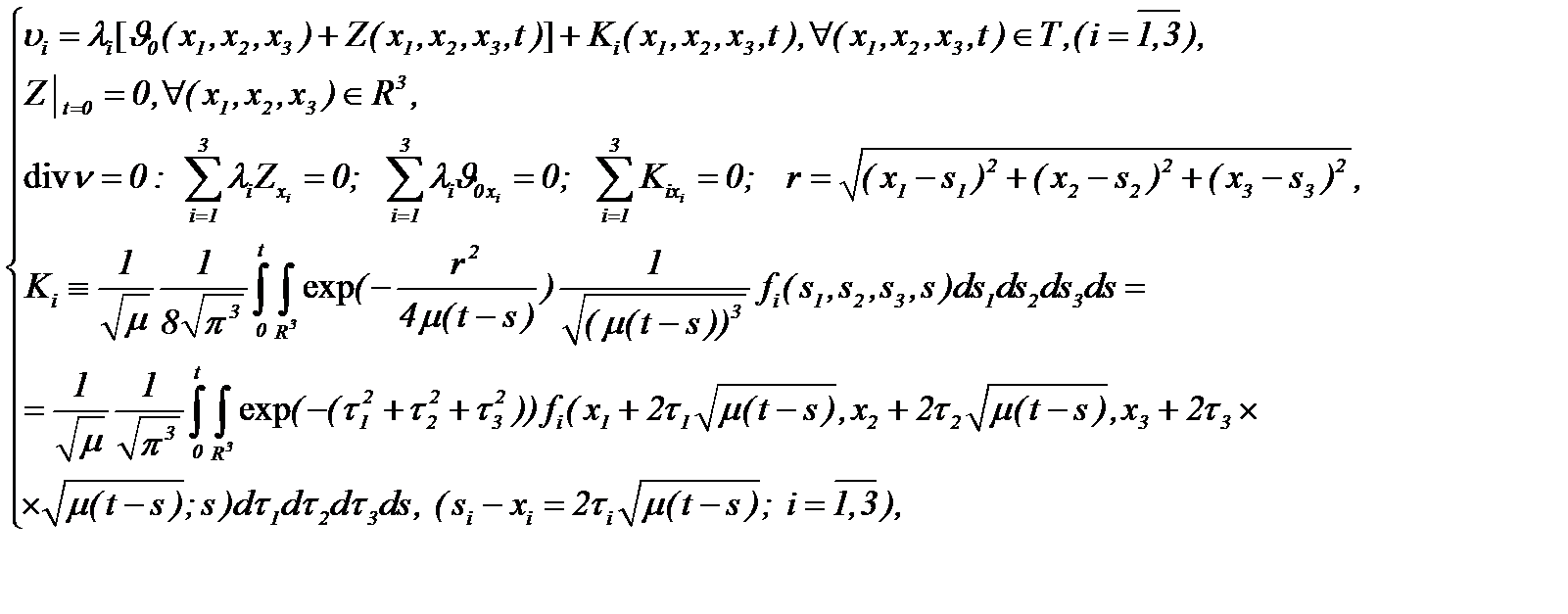 (6.16)
(6.16) (6.17)
(6.17)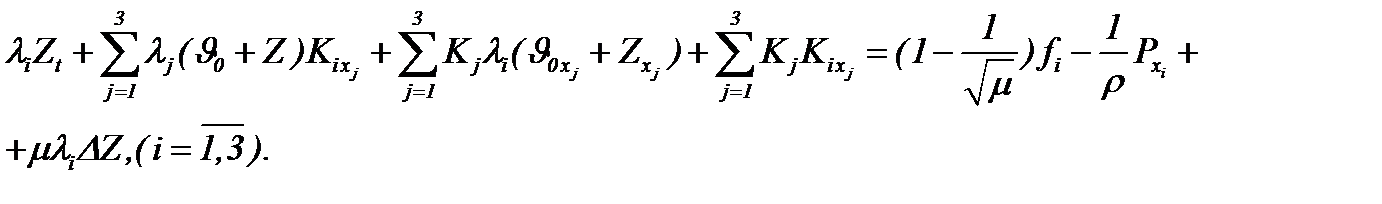 (6.18)
(6.18)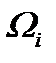 рассматриваем
рассматриваем 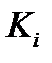 , получим
, получим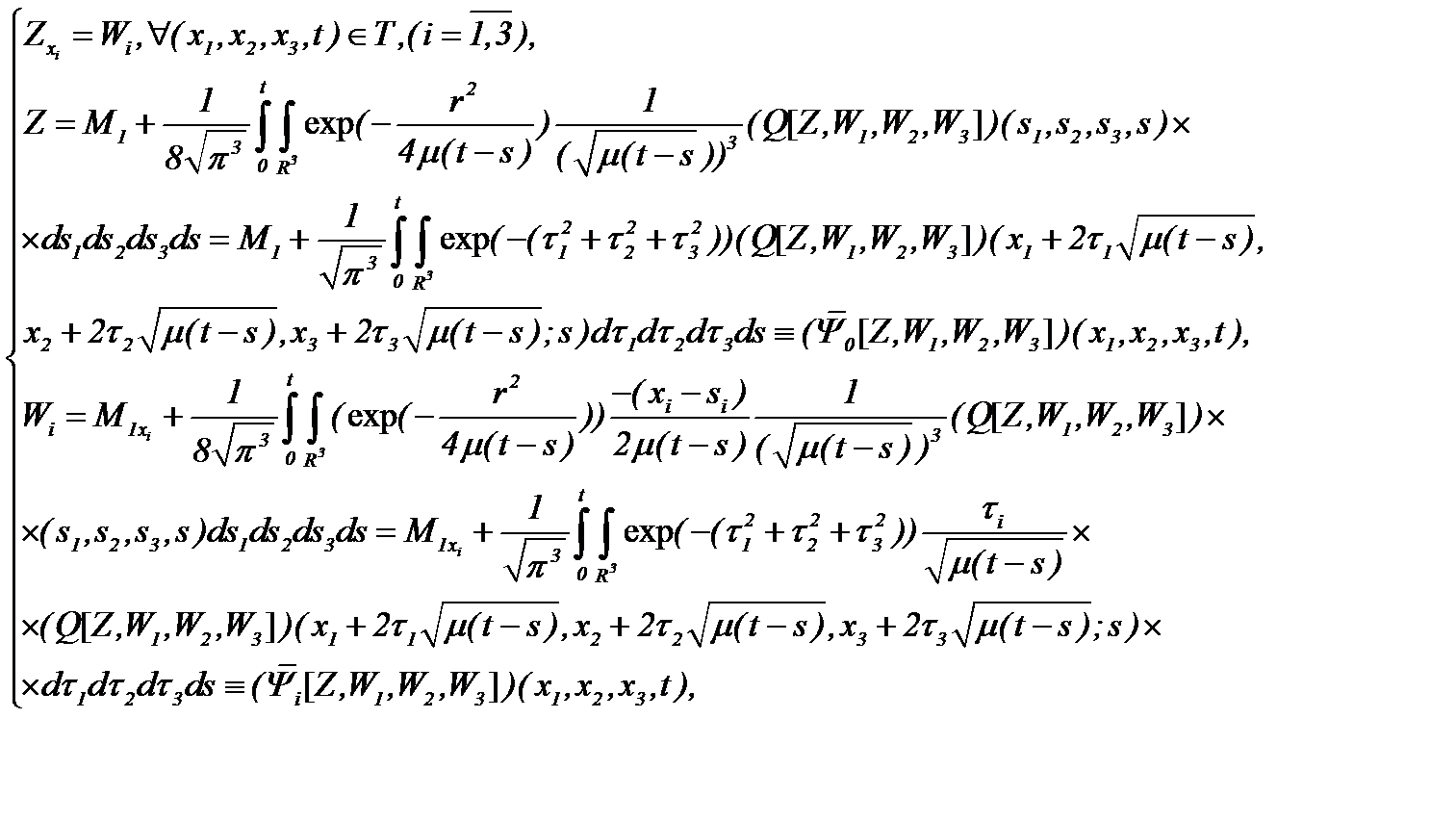 (6.19)
(6.19)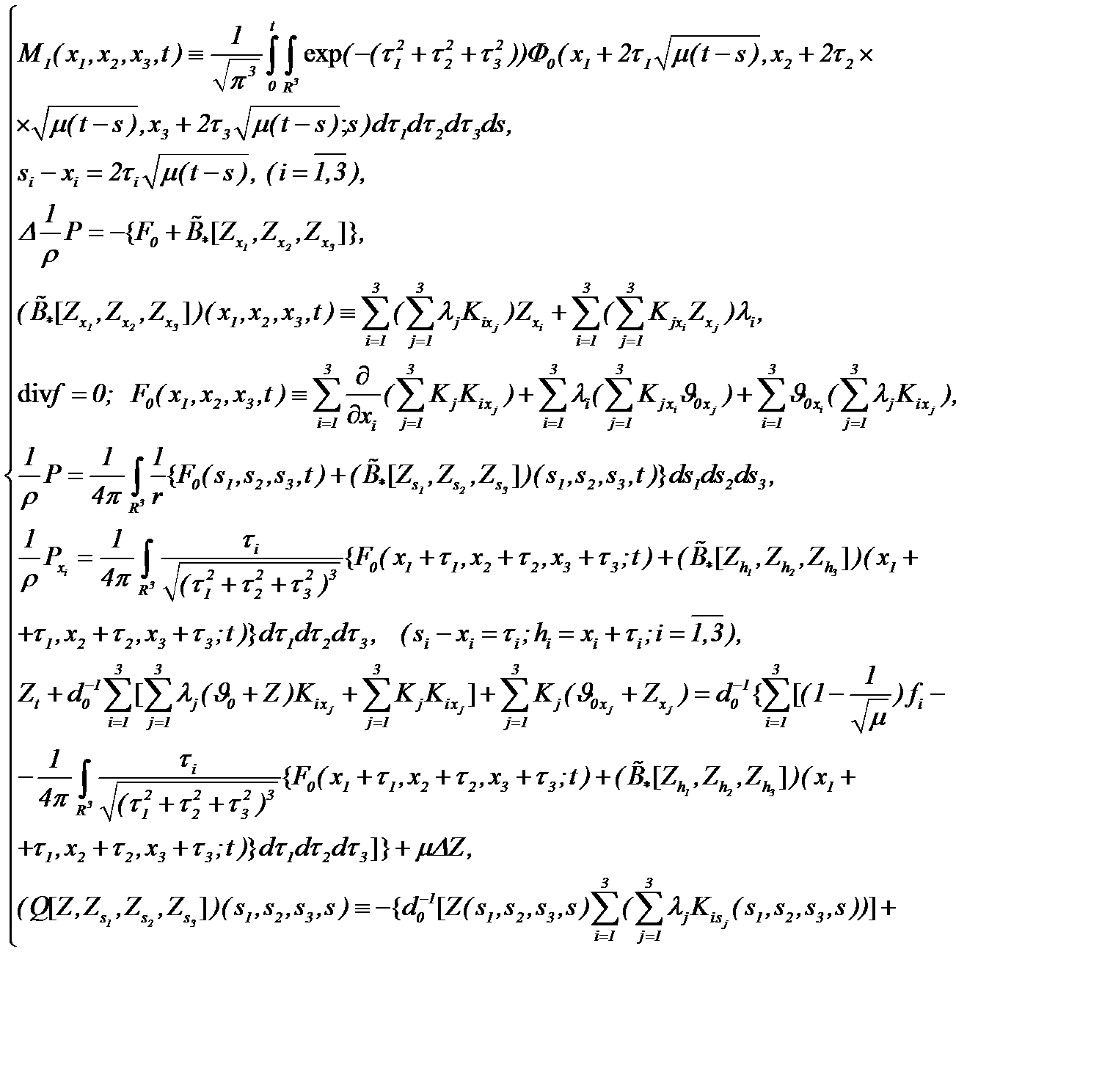
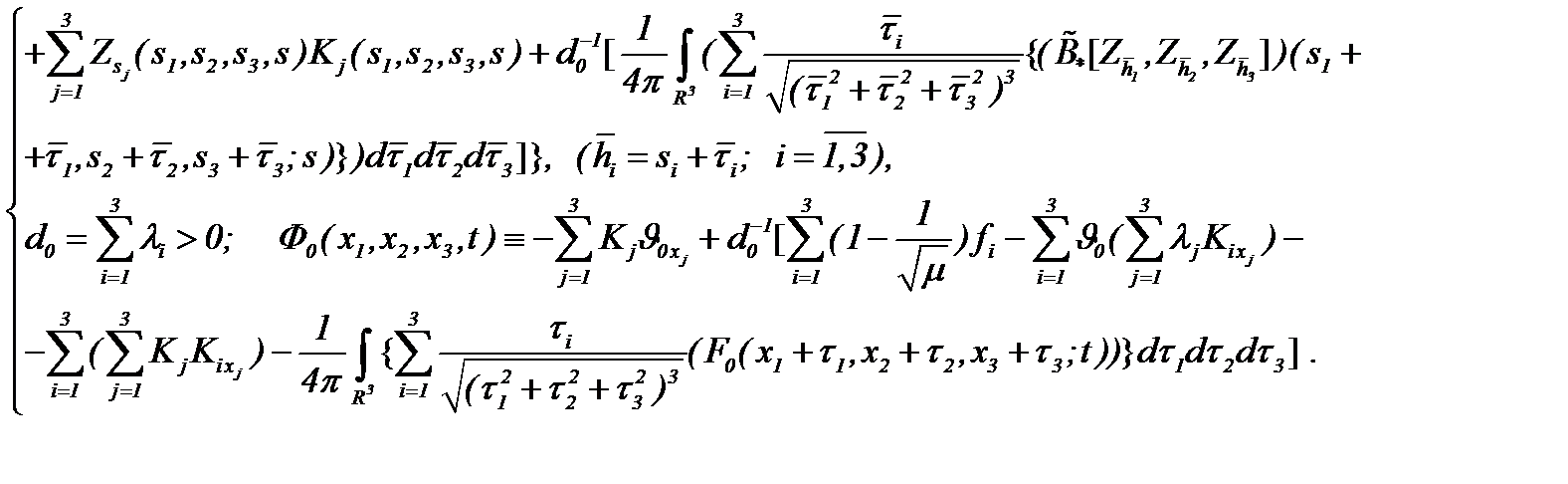
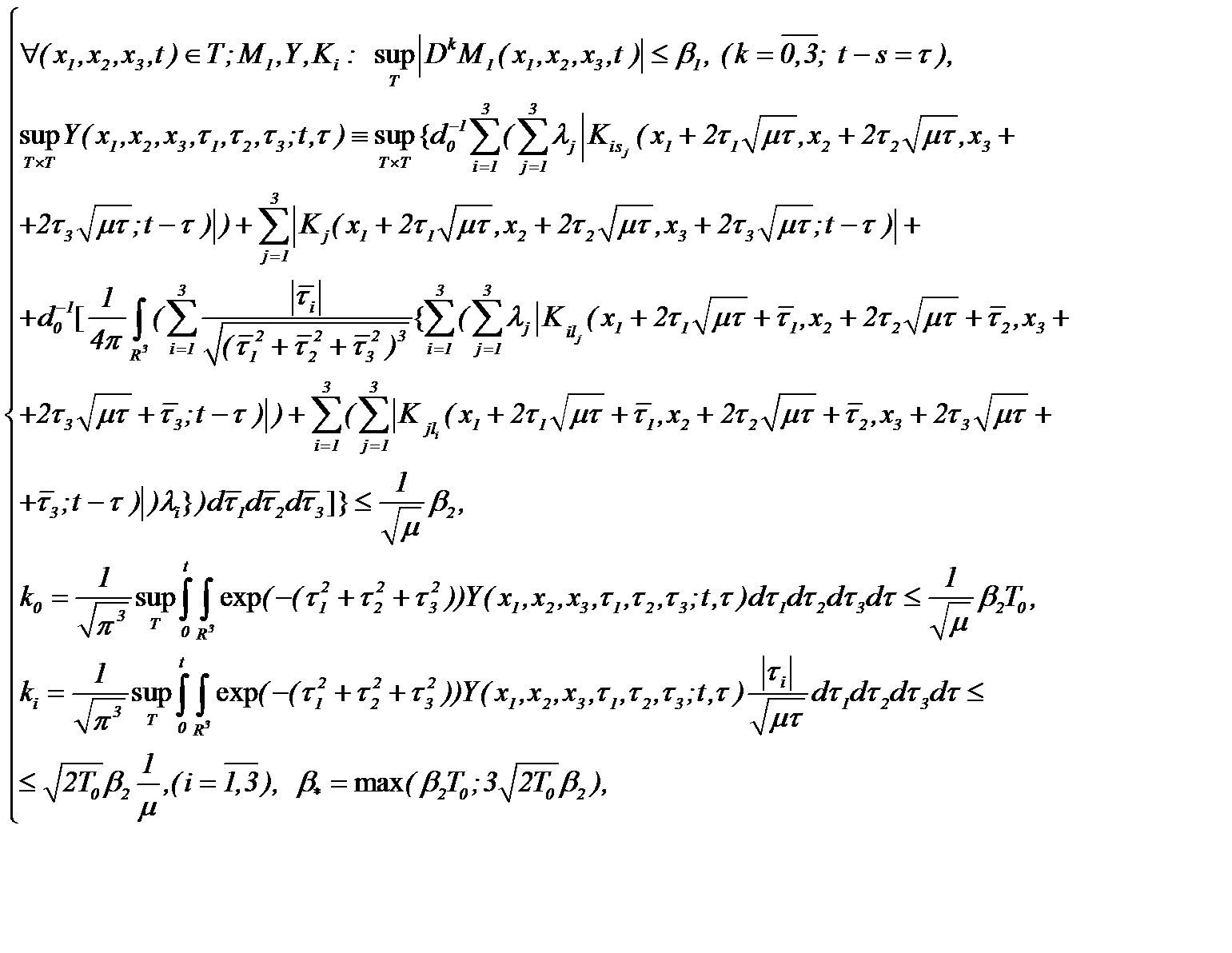 (6.20)
(6.20)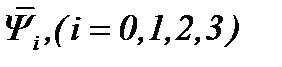 допускают условия
допускают условия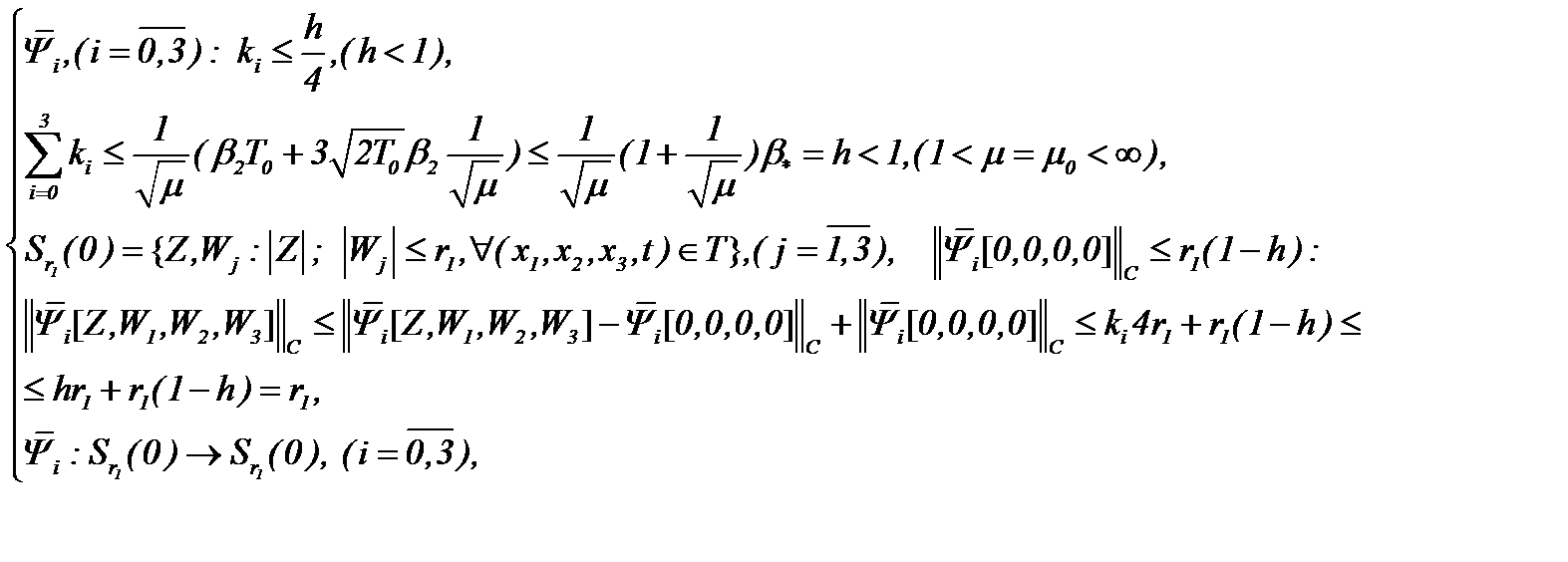 (6.21)
(6.21)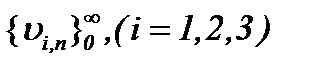 сходятся к пределу
сходятся к пределу 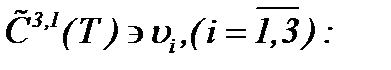
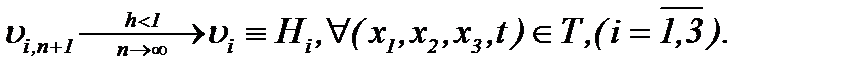 (6.22)
(6.22)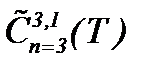 , когда
, когда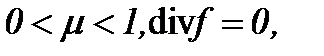 или
или