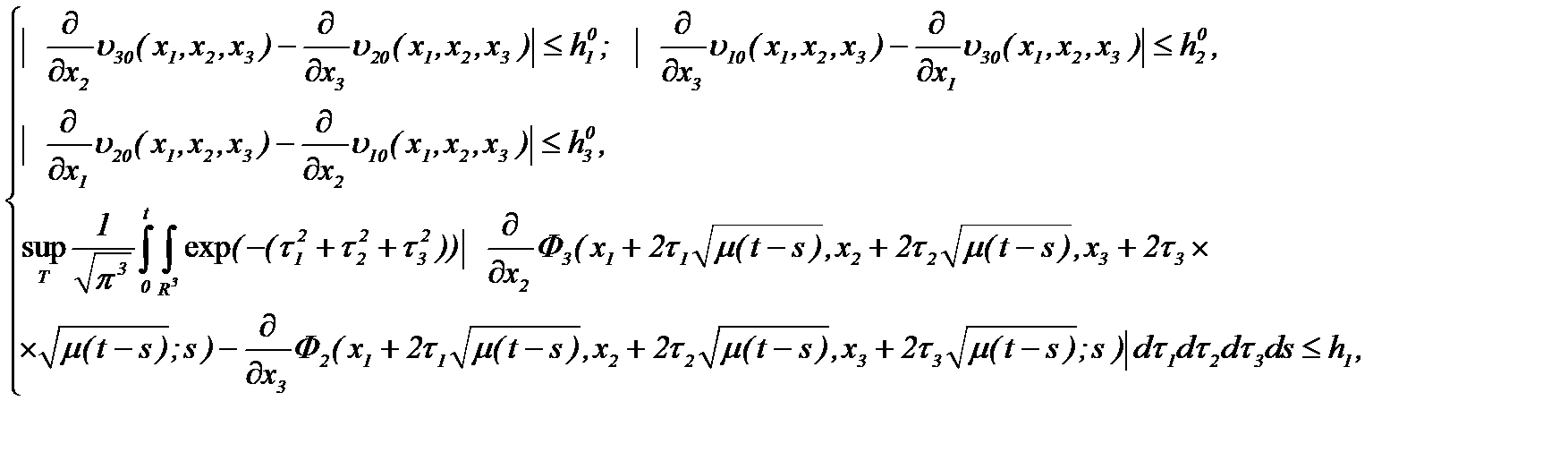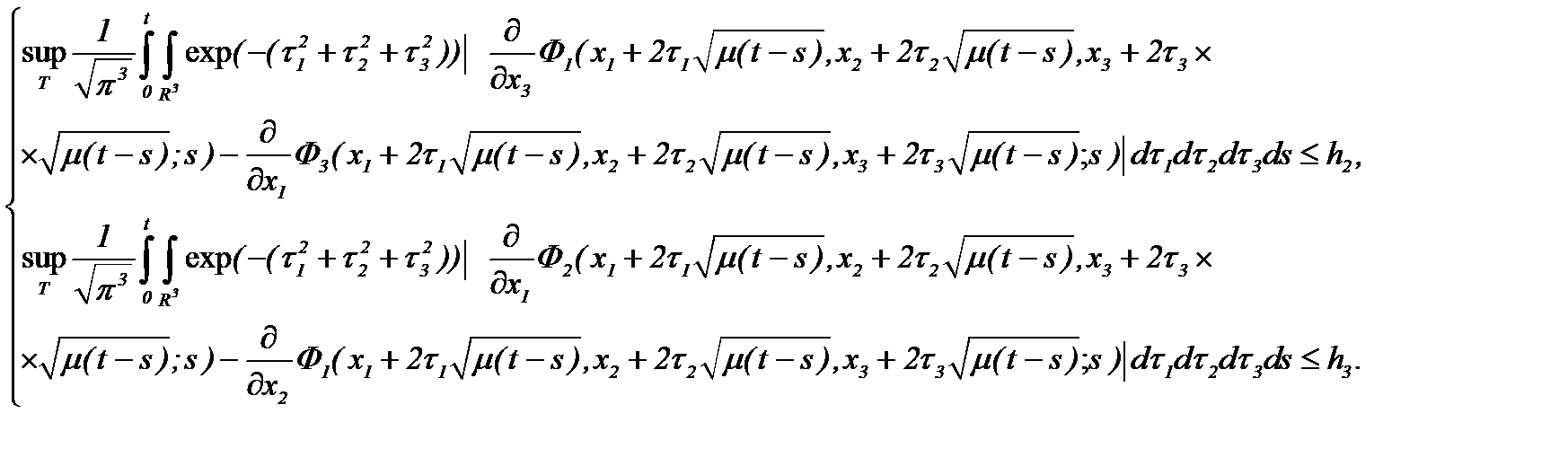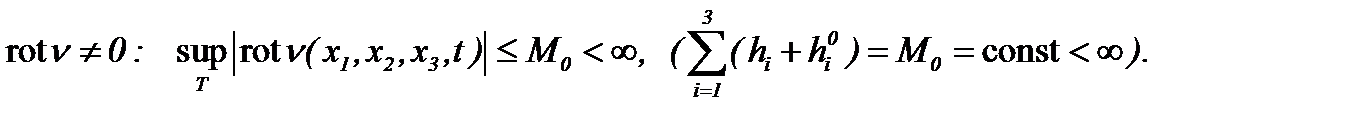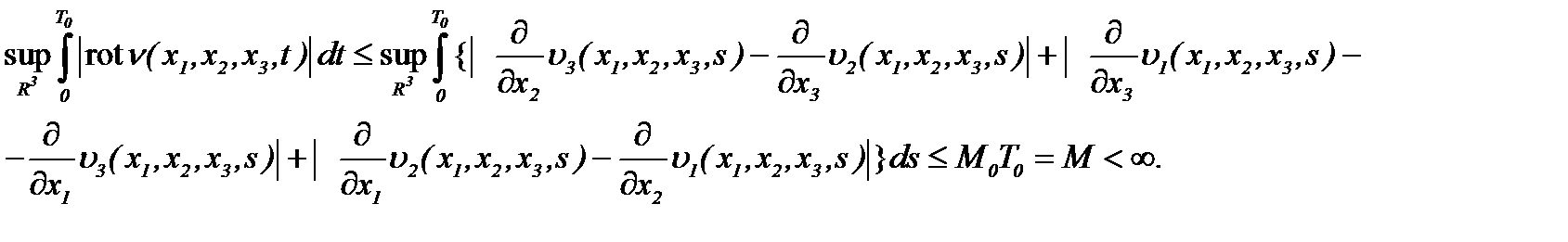Критерий регулярности Билла-Като-Мажда первоначально получен для решений 3D уравнений Эйлера [2], однако имеет место для решений 3D уравнений Навье-Стокса [5], поскольку вправе рассматриваться как принцип продолжения для сильных решений. Дальнейшее обобщение было дано в [8], где условие регулярности интегралов относительно параметра вязкости выражено в терминах времени интегрируемости. С другой стороны, поскольку известны неравенства для априорных оценок в зависимости от пространств, то для доказательства этого критерия достаточно соблюсти, например, следующее неравенство [5]:
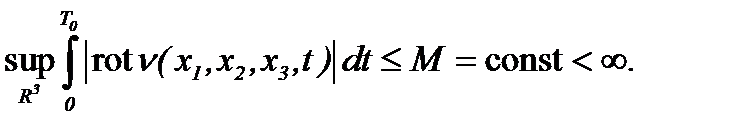 (2.24)
(2.24)
На основании результатов теоремы 1 решение систем (1.1) представимо в виде (2.19), где глобальное существование решений принимается в классе 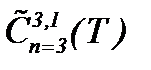 с точки зрения исходных данных, удовлетворяющих (2.19). Отрадно, что результаты теоремы 2* приводят к глобальным классическим решениям уравнений Навье-Стокса, поскольку известно, что классическое решение приемлемо [5], если критерий Билла-Като-Мажда выполнен.
с точки зрения исходных данных, удовлетворяющих (2.19). Отрадно, что результаты теоремы 2* приводят к глобальным классическим решениям уравнений Навье-Стокса, поскольку известно, что классическое решение приемлемо [5], если критерий Билла-Като-Мажда выполнен.
Действительно, при выполнении условий теоремы 2* имеем
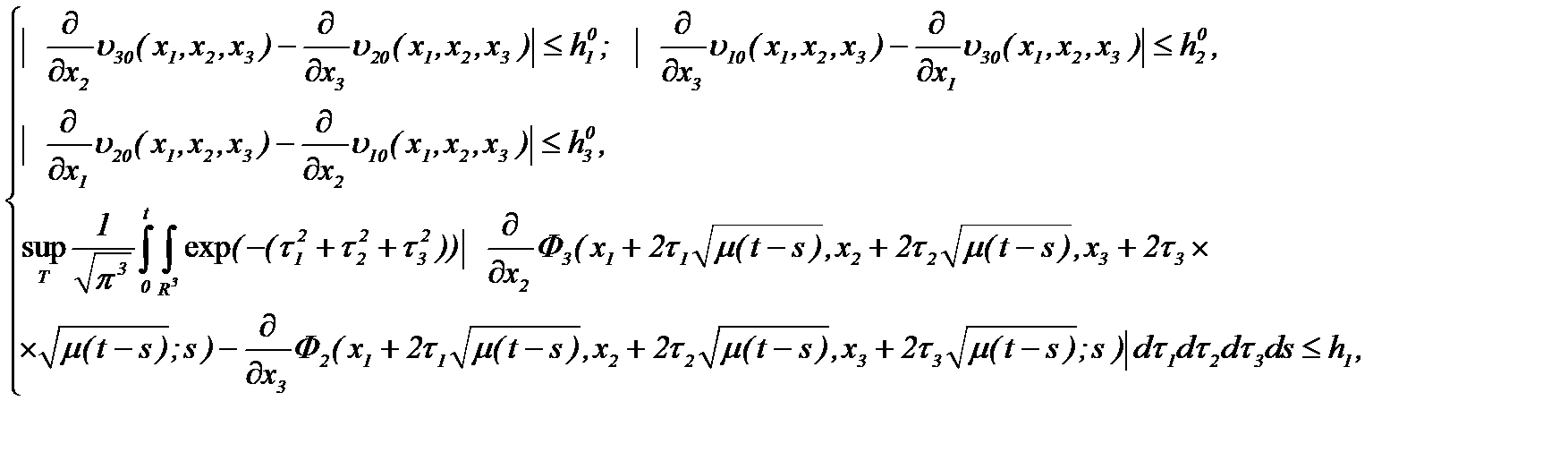
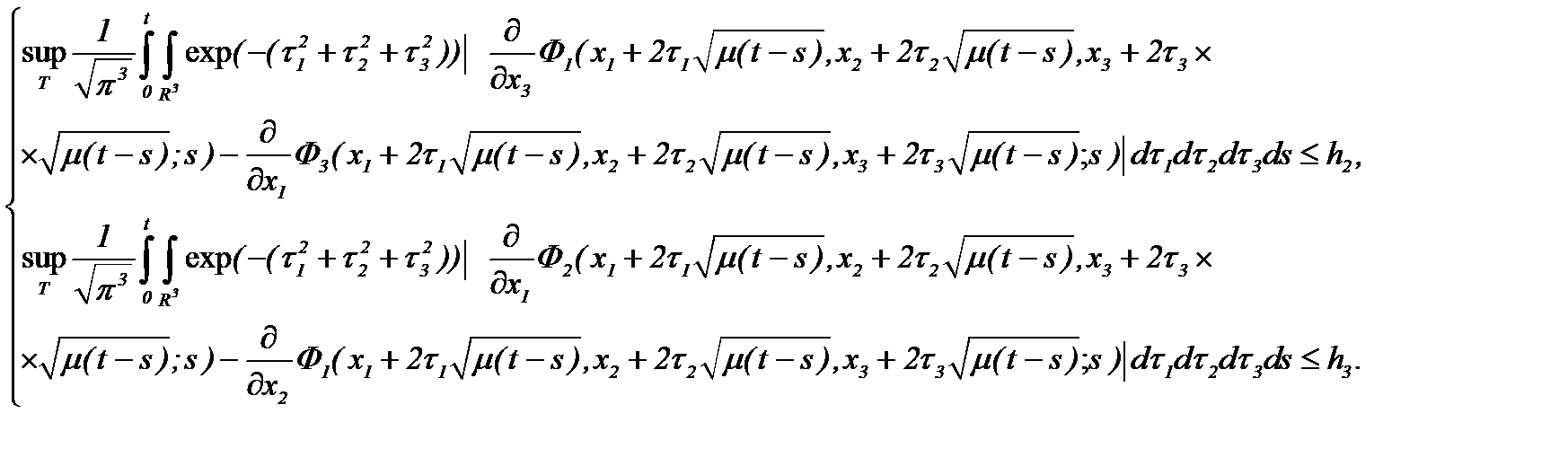
Тогда получим оценку
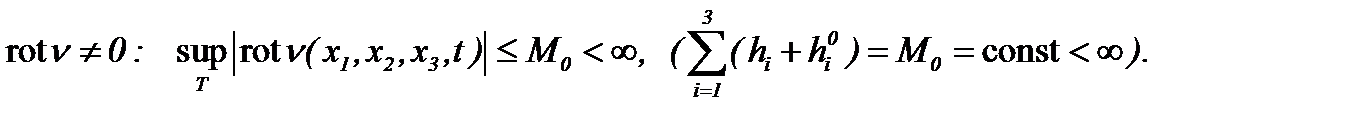
Как следствие, имеем (см. (2.24)):
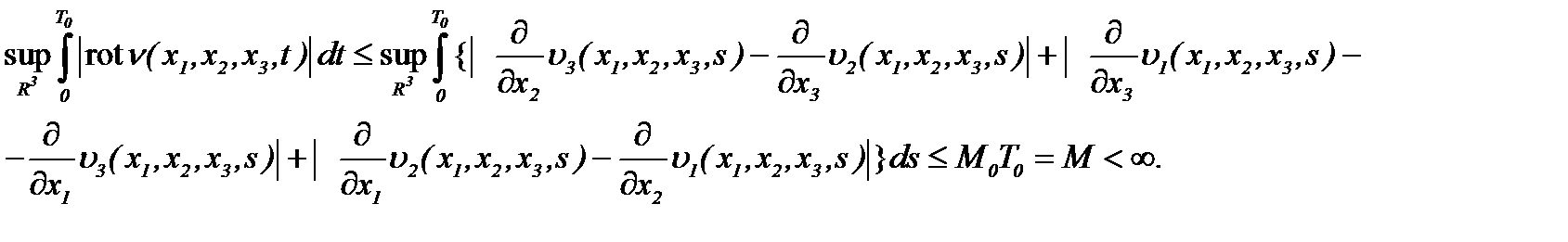
Значит, выведенная нами оценка является оценкой типа Билла-Като-Мажда [5].





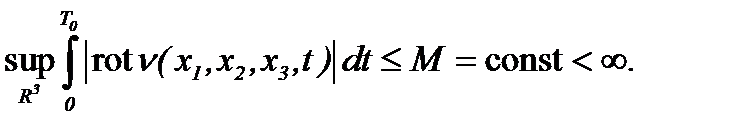 (2.24)
(2.24)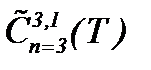 с точки зрения исходных данных, удовлетворяющих (2.19). Отрадно, что результаты теоремы 2* приводят к глобальным классическим решениям уравнений Навье-Стокса, поскольку известно, что классическое решение приемлемо [5], если критерий Билла-Като-Мажда выполнен.
с точки зрения исходных данных, удовлетворяющих (2.19). Отрадно, что результаты теоремы 2* приводят к глобальным классическим решениям уравнений Навье-Стокса, поскольку известно, что классическое решение приемлемо [5], если критерий Билла-Като-Мажда выполнен.