4.4. Модификация метода (4.2), когда 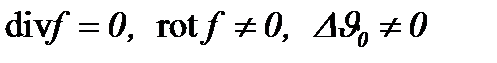
Рассмотрим разновидность основного метода (4.2) по пункту 4.1, когда начальные компоненты скорости и функции 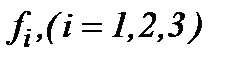 удовлетворяют условиям
удовлетворяют условиям
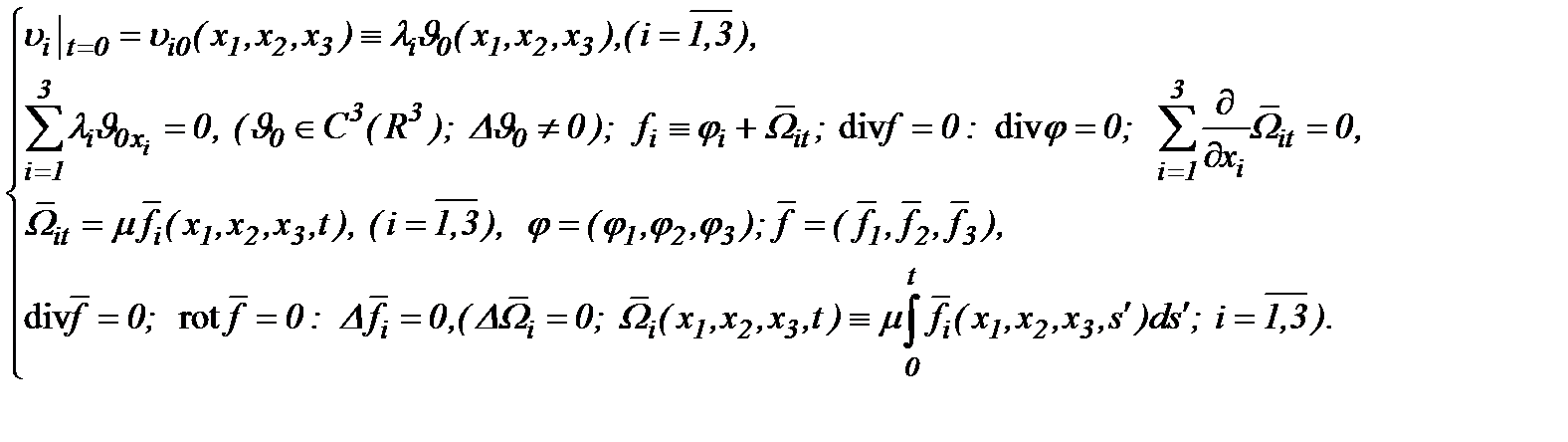 (4.36)
(4.36)
Тогда функции 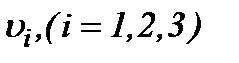 представимы в виде
представимы в виде
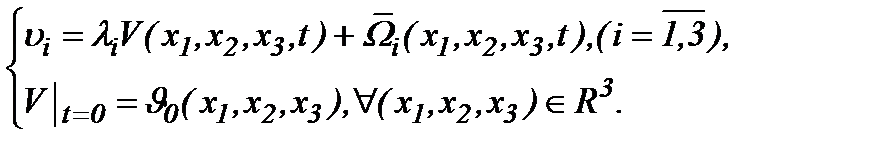 (4.37)
(4.37)
Теперь, используя формулы (4.36), (4.37) и
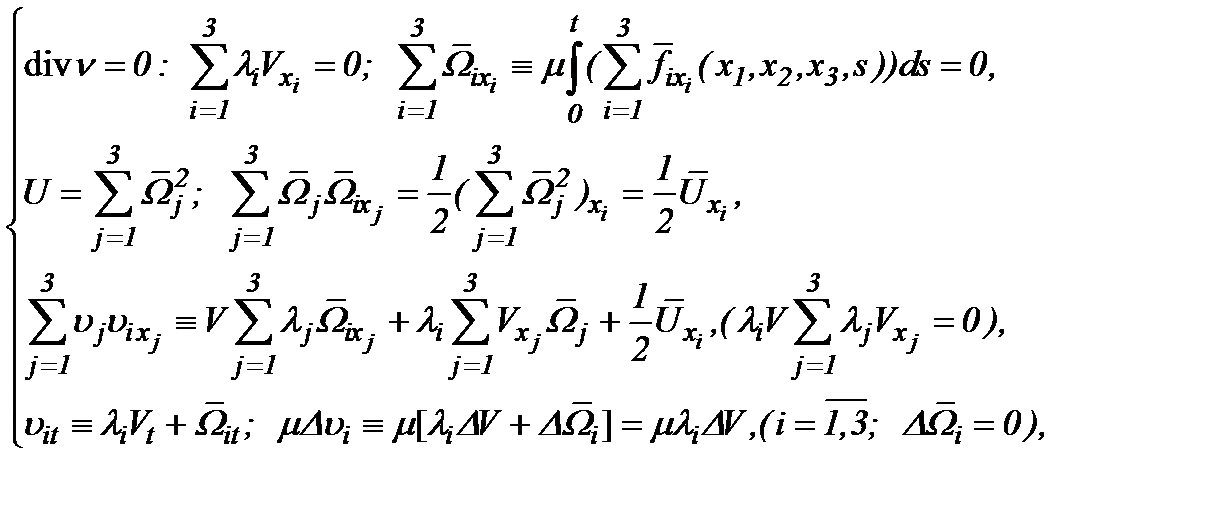 (4.38)
(4.38)
из уравнений Навье-Стокса (1.1) получим эквивалентную систему
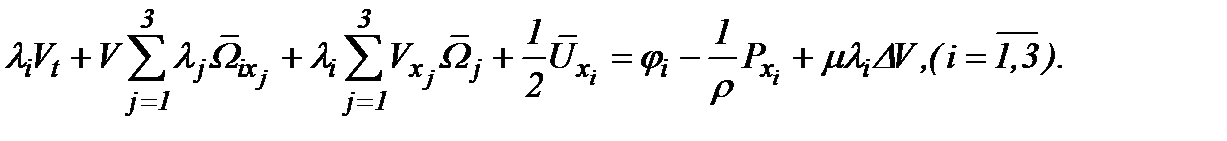 (4.39)
(4.39)
Далее, из системы (4.39) с учетом условий (4.36) – (4.38), применяя алгоритм АПС, имеем уравнение
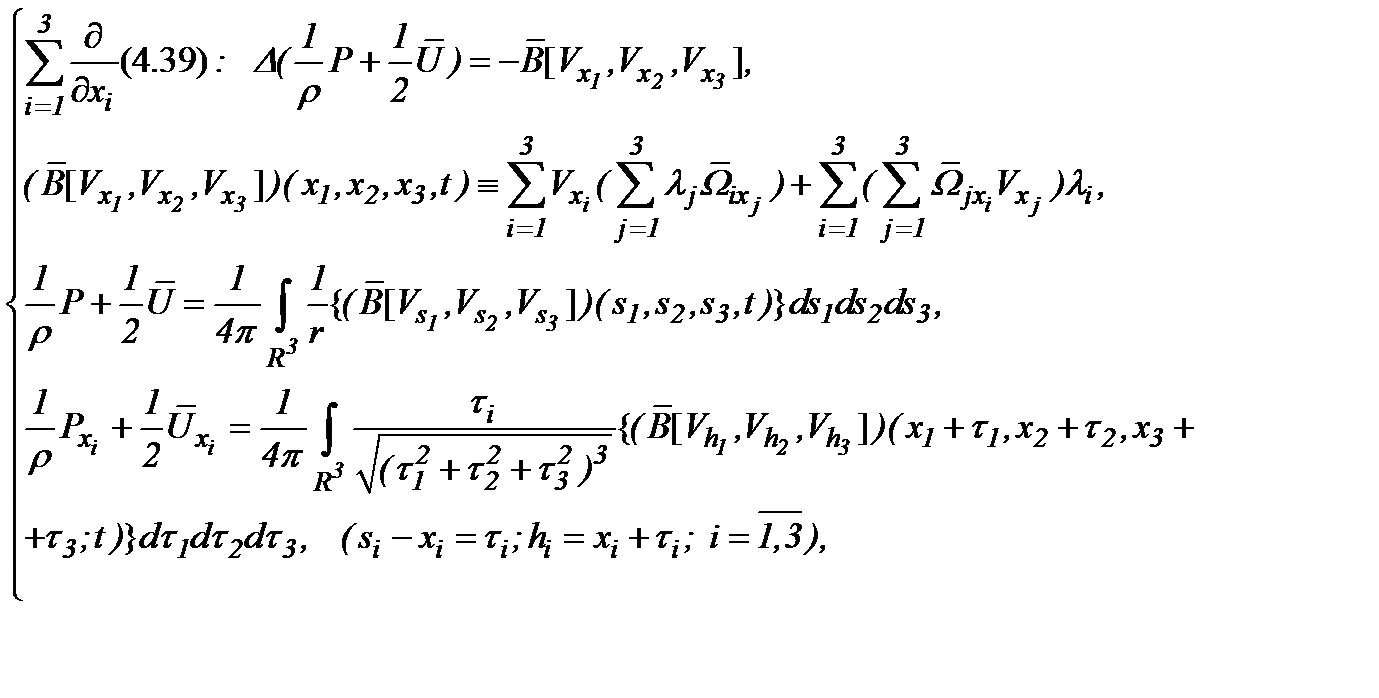 (4.40)
(4.40)
так как при математических преобразованиях системы (4.39) соблюдаются условия
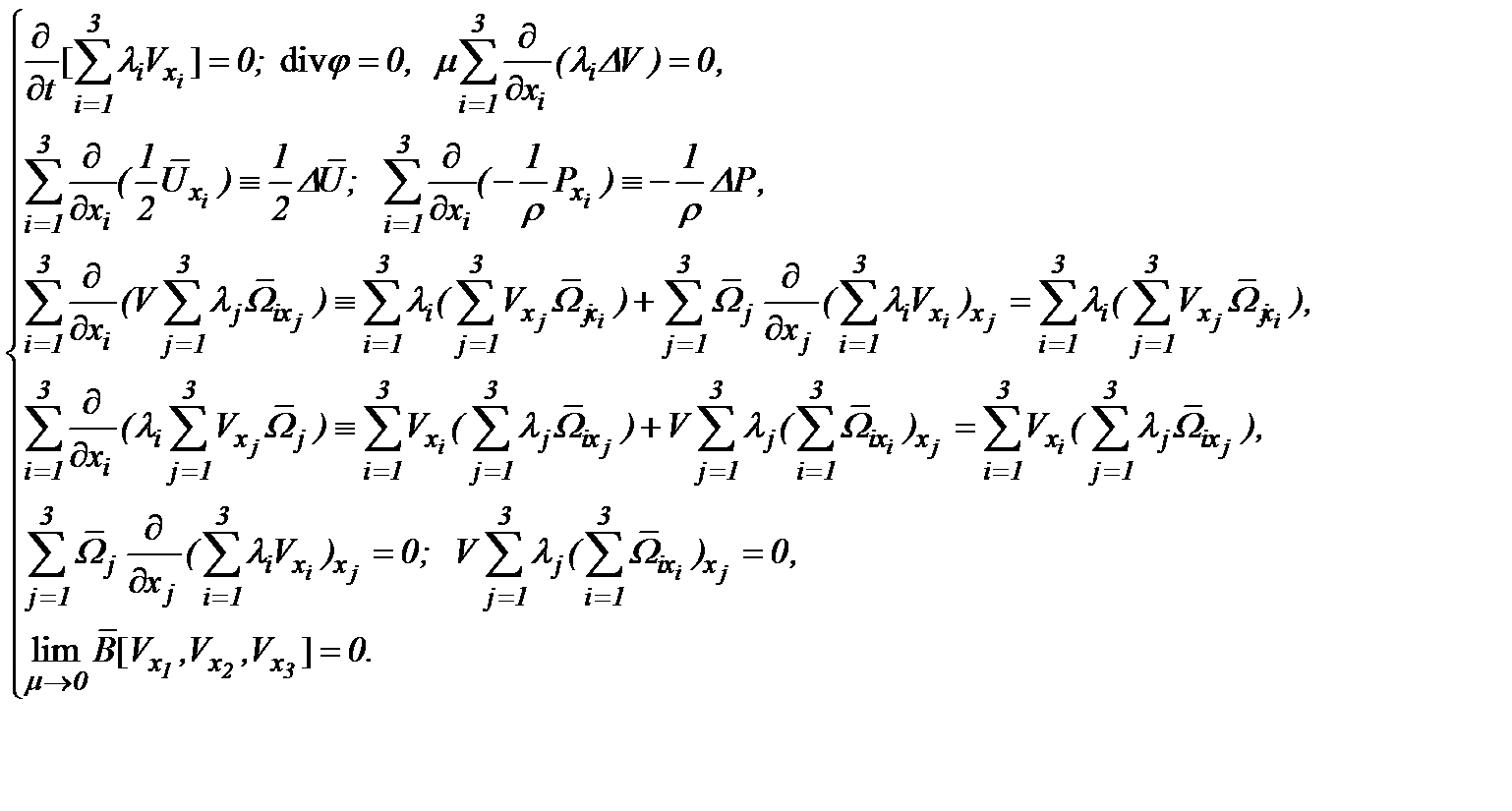
Следовательно, система (4.39) на основе (4.40) эквивалентно преобразуется к виду
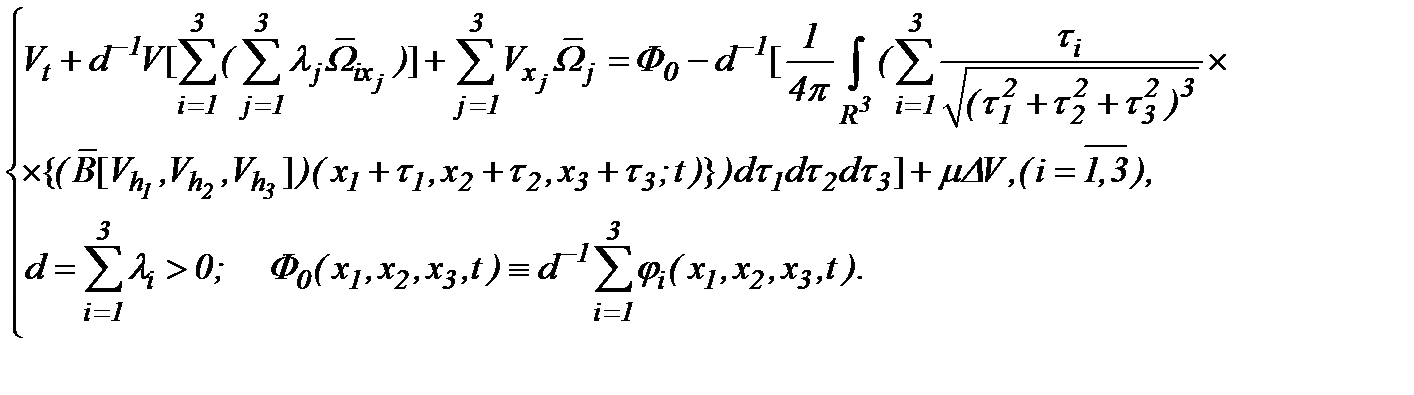 (4.41)
(4.41)
Но, теперь, из (4.41) следует
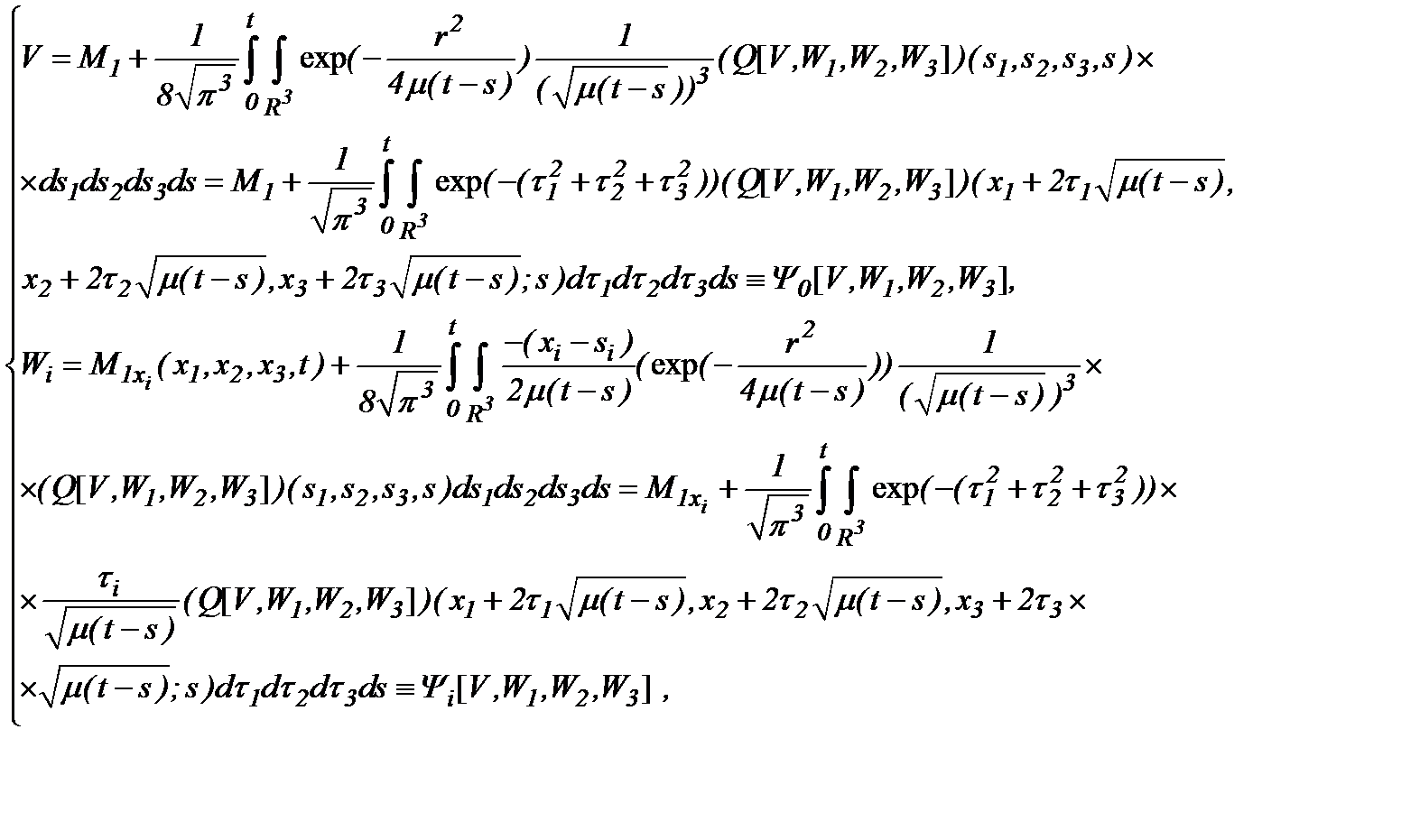 (4.42)
(4.42)
где

В таком виде система (4.42) содержит неизвестные функции 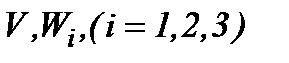 и состоит из четырех интегральных уравнений Вольтерра-Абеля второго рода по переменной
и состоит из четырех интегральных уравнений Вольтерра-Абеля второго рода по переменной 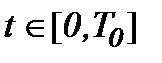 .
.
Итак, пусть относительно известных данных предполагаются выполненными условия
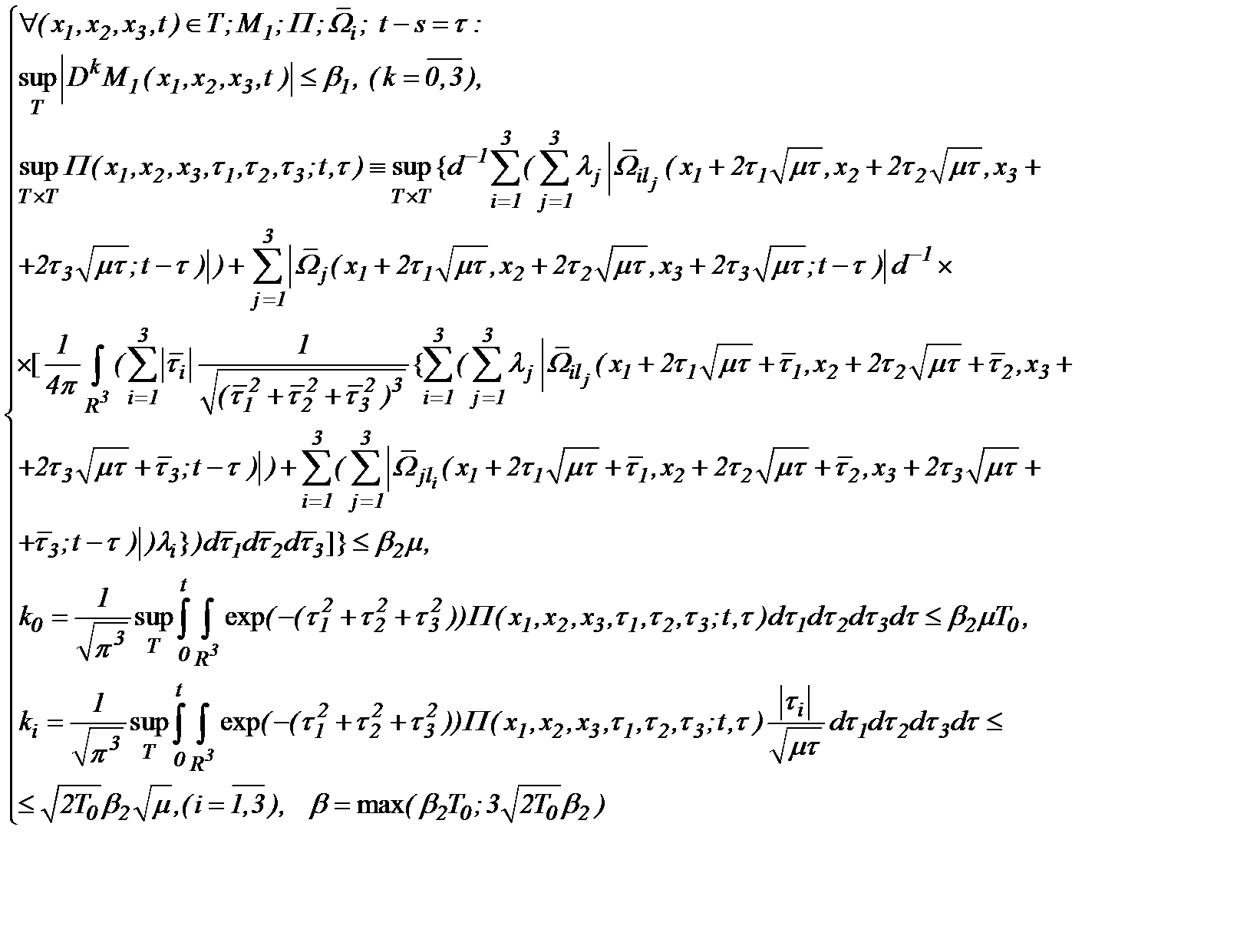 (4.43)
(4.43)
и
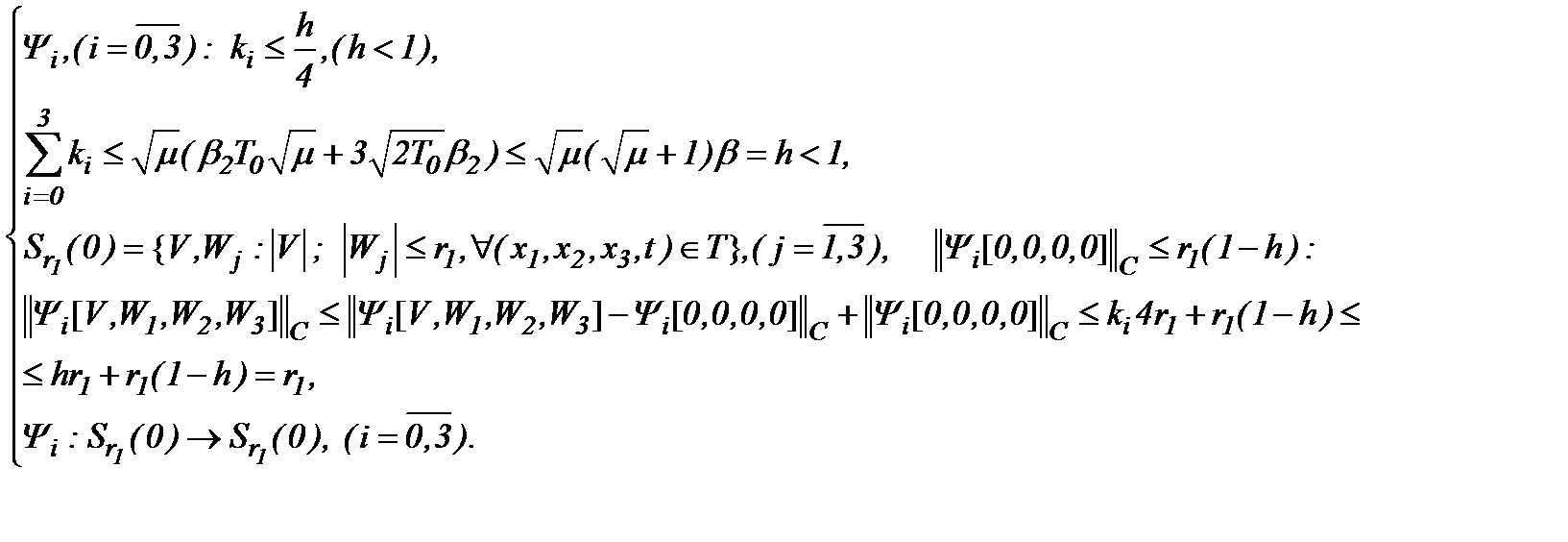 (4.44)
(4.44)
Тогда на основании (4.31) – (4.33) существует единственное решение системы (4.42), которое определяется по методу Пикара. Значит, относительно последовательности функций 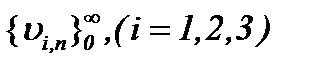 допускаются все выводы метода Пикара (4.31), указанные в предыдущих пунктах. Поэтому последовательность функций
допускаются все выводы метода Пикара (4.31), указанные в предыдущих пунктах. Поэтому последовательность функций 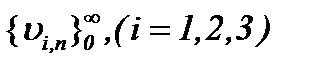 сходится к пределу
сходится к пределу 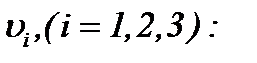
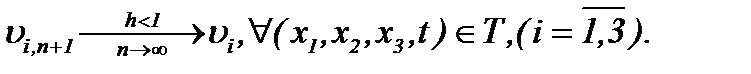 (4.45)
(4.45)
Из полученных результатов следует, что задача Навье-Стокса (1.1) – (1.3) в случае (4.36), (4.37) и (4.45) с достаточно гладкими начальными данными имеет условно-гладкое единственное решение в 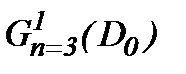 , так как
, так как 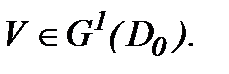 Поэтому результаты формулируются следующей теоремой.
Поэтому результаты формулируются следующей теоремой.
Теорема 5. Задача Навье-Стокса при условиях (1.2), (1.3), (4.36), (4.37) и (4.45) имеет условно-гладкое единственное решение в 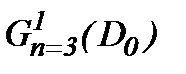 .
.
Замечание 5. Алгоритм (4.37) применим, как в случае равенства, так и неравенства, т.е. когда 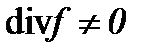 . В самом деле, если
. В самом деле, если
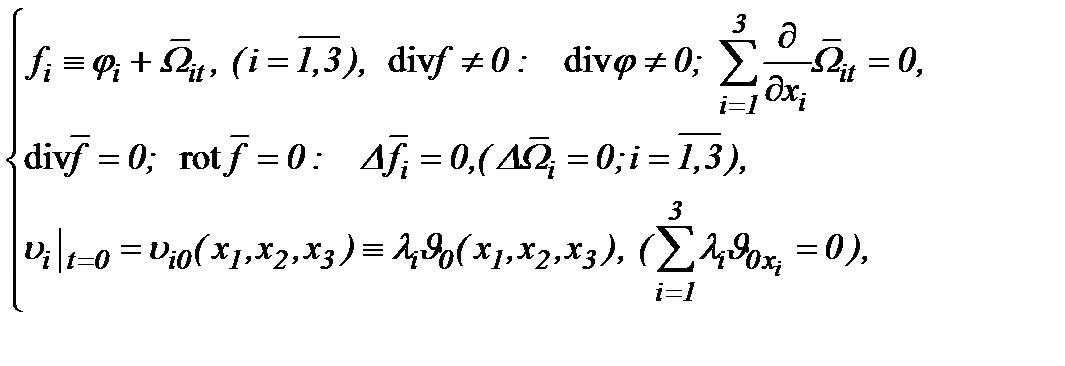 (4.46)
(4.46)
то на основе (4.39) – (4.41) имеем
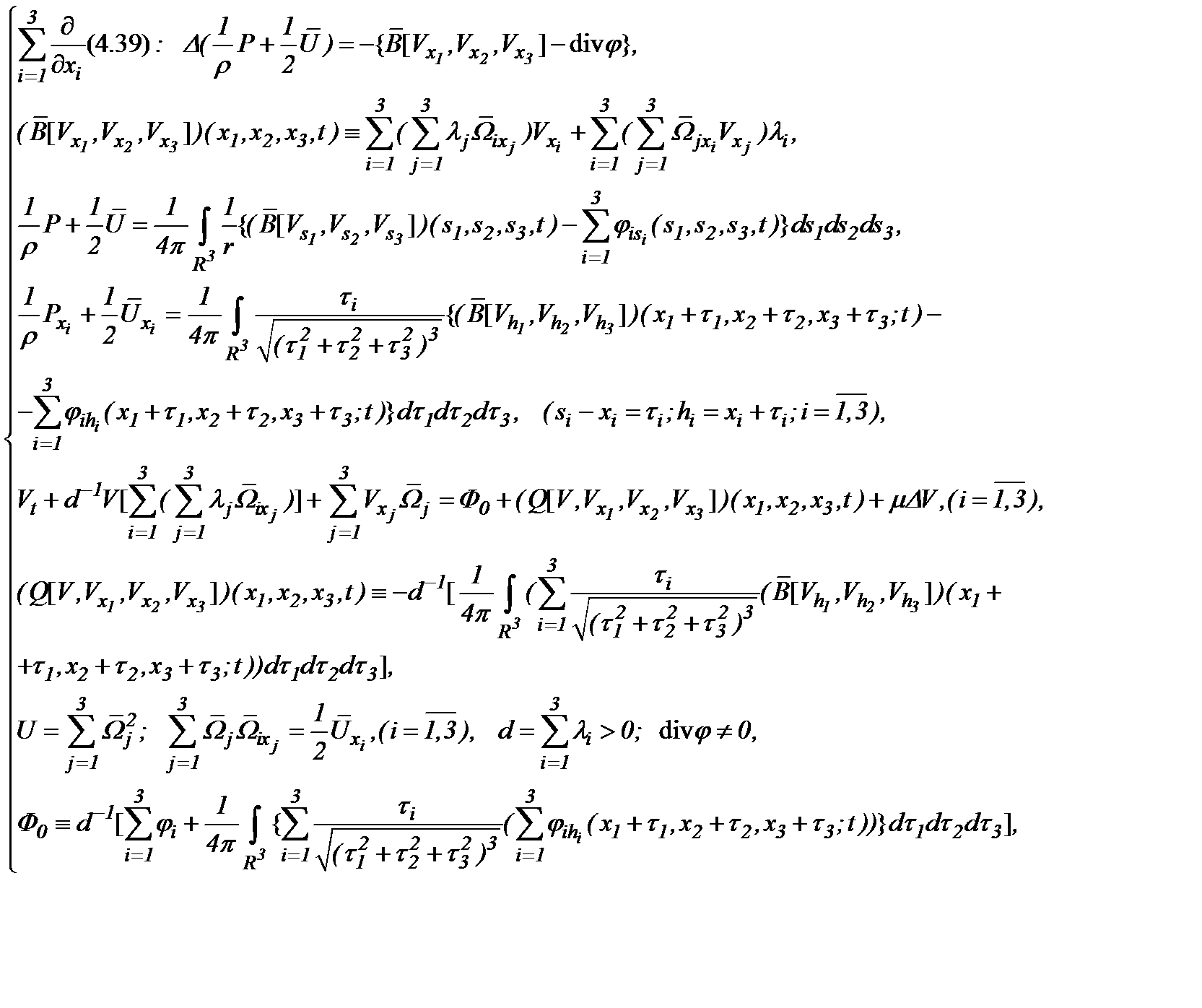
т.е. получили выражение (4.42) следующего вида
 (4.42)*
(4.42)*
Поскольку справедливо (4.44), то решение системы (4.42)* можем найти по методу Пикара, при этом на основании (4.31) – (4.33) имеем сходимость по формуле (4.45). Значит, как и с аналогичными результатами теоремы 5, задача Навье-Стокса при условиях (1.2), (1.3), (4.45), (4.46) имеет единственное решение в 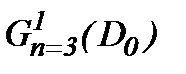 .
.





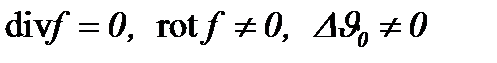
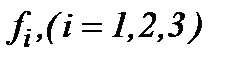 удовлетворяют условиям
удовлетворяют условиям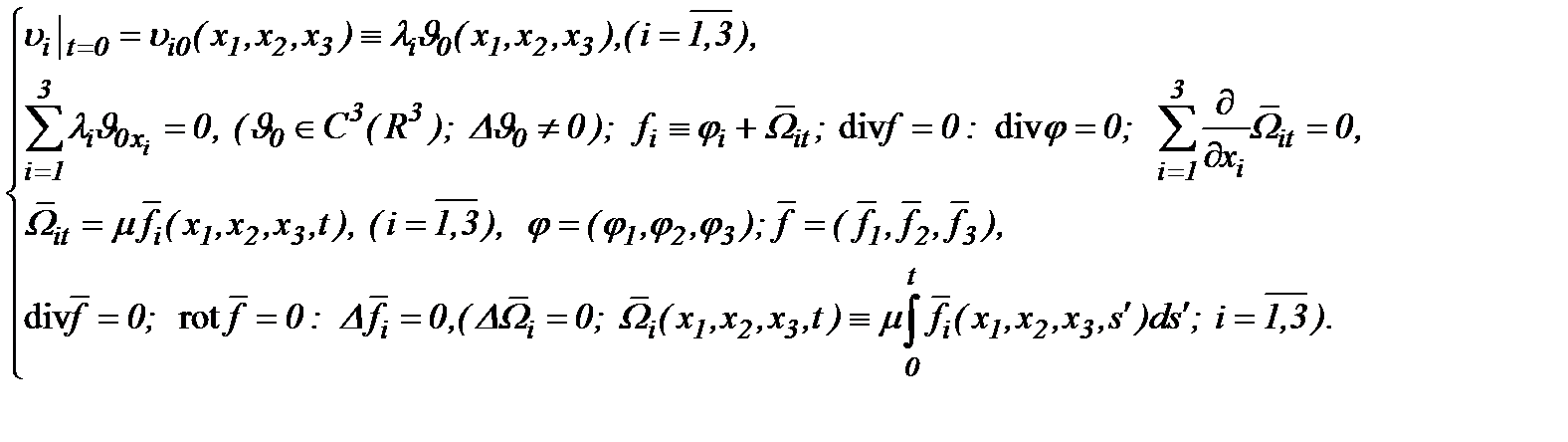 (4.36)
(4.36)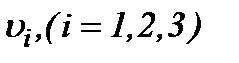 представимы в виде
представимы в виде 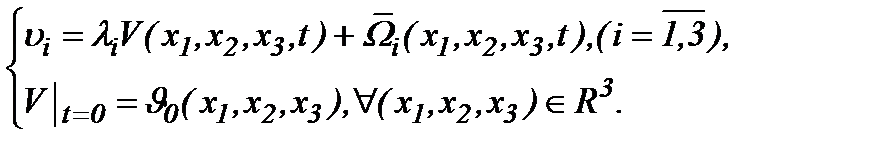 (4.37)
(4.37)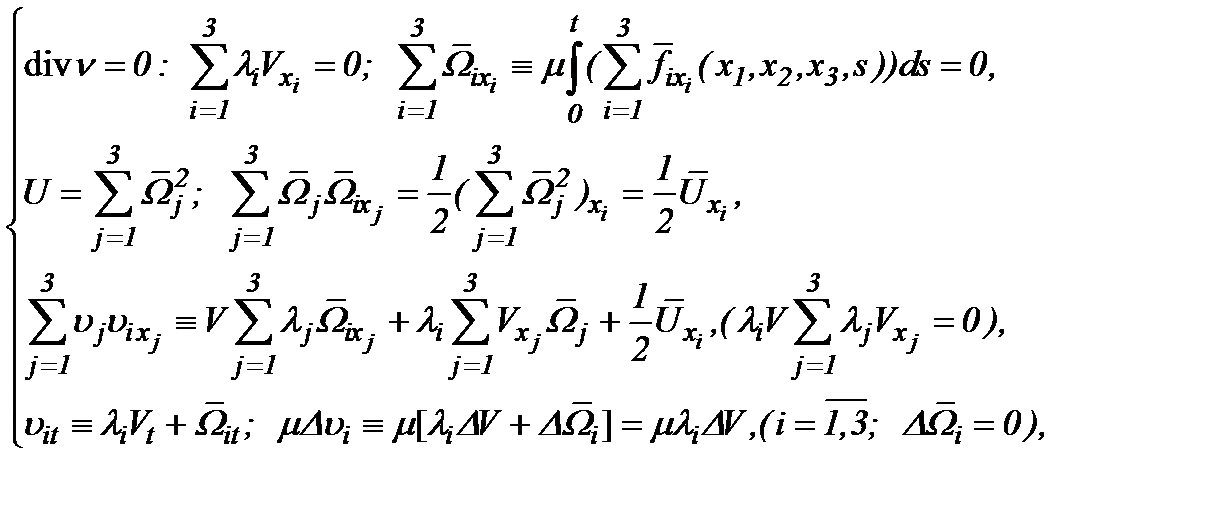 (4.38)
(4.38)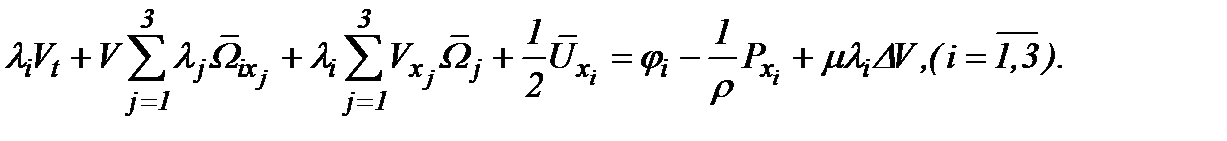 (4.39)
(4.39)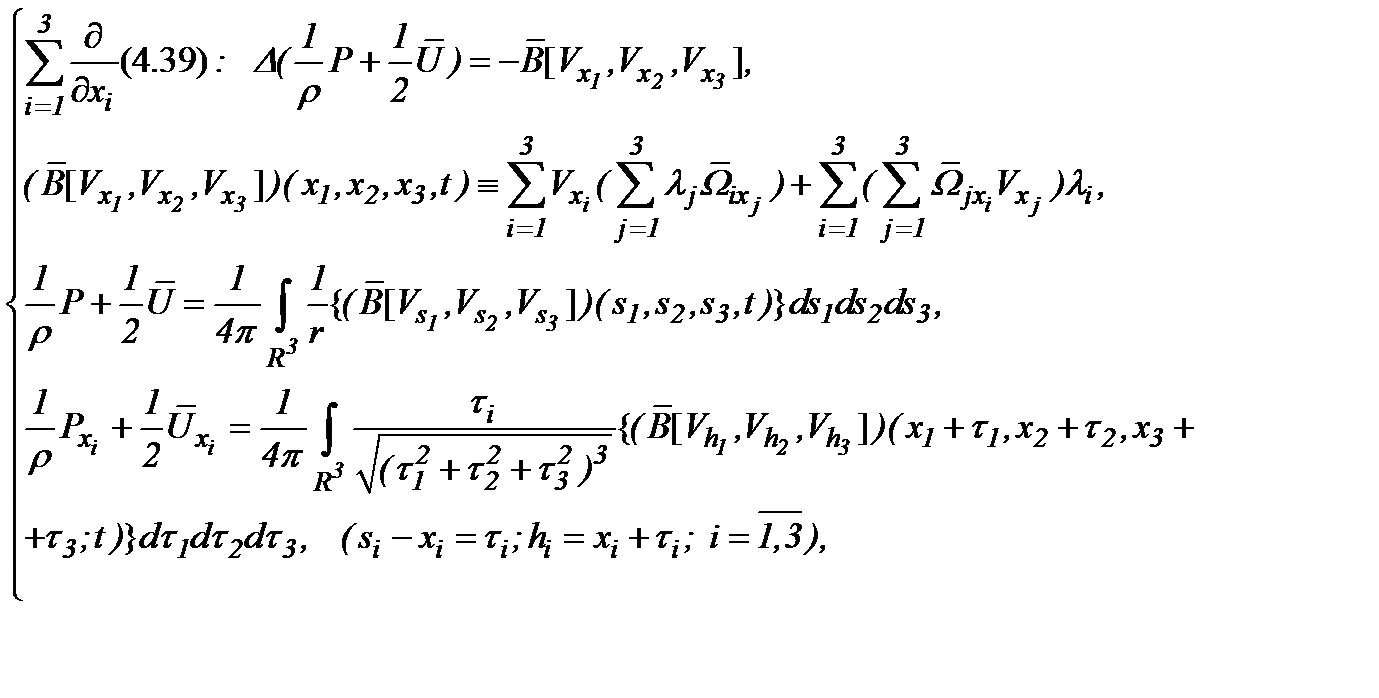 (4.40)
(4.40)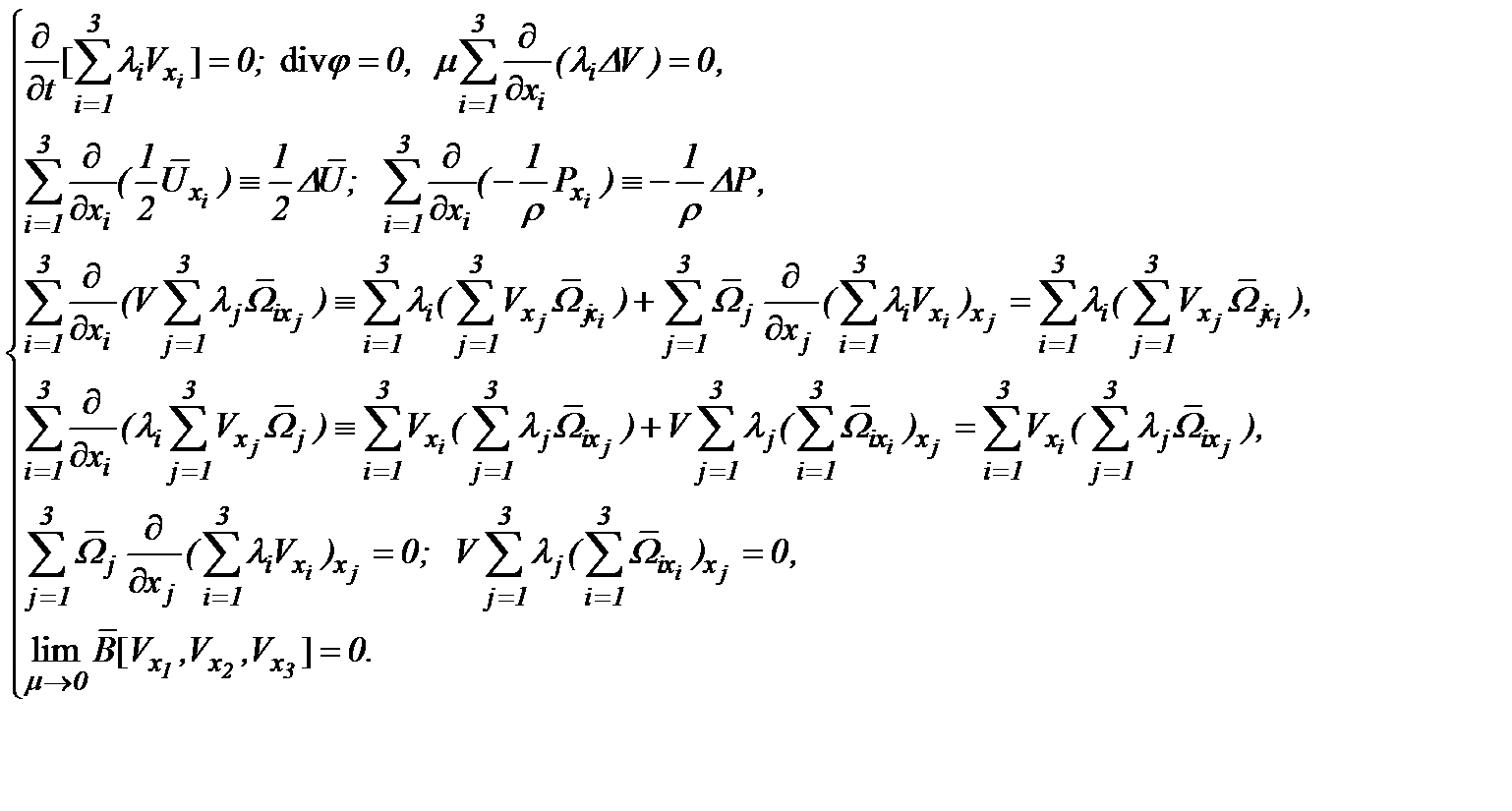
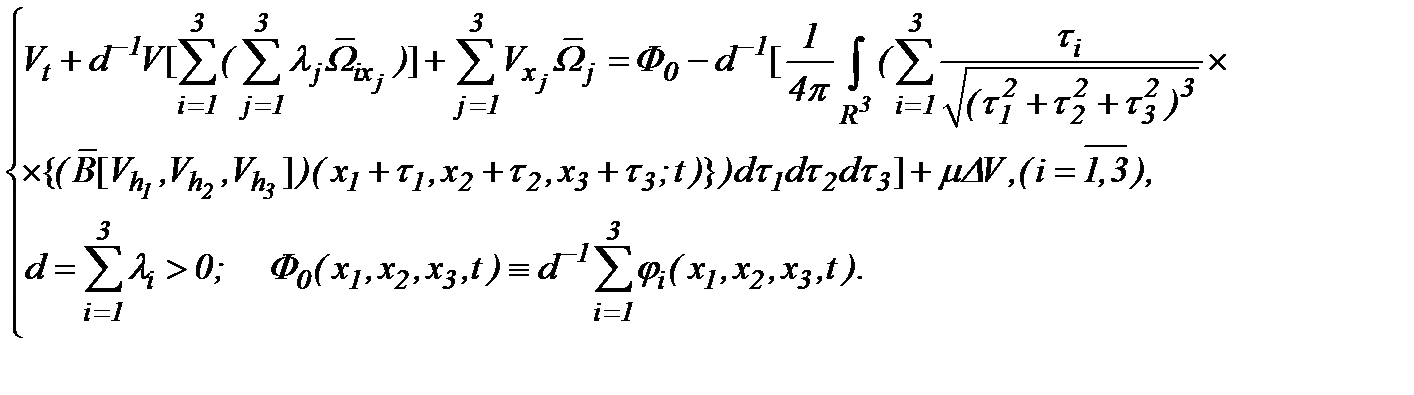 (4.41)
(4.41)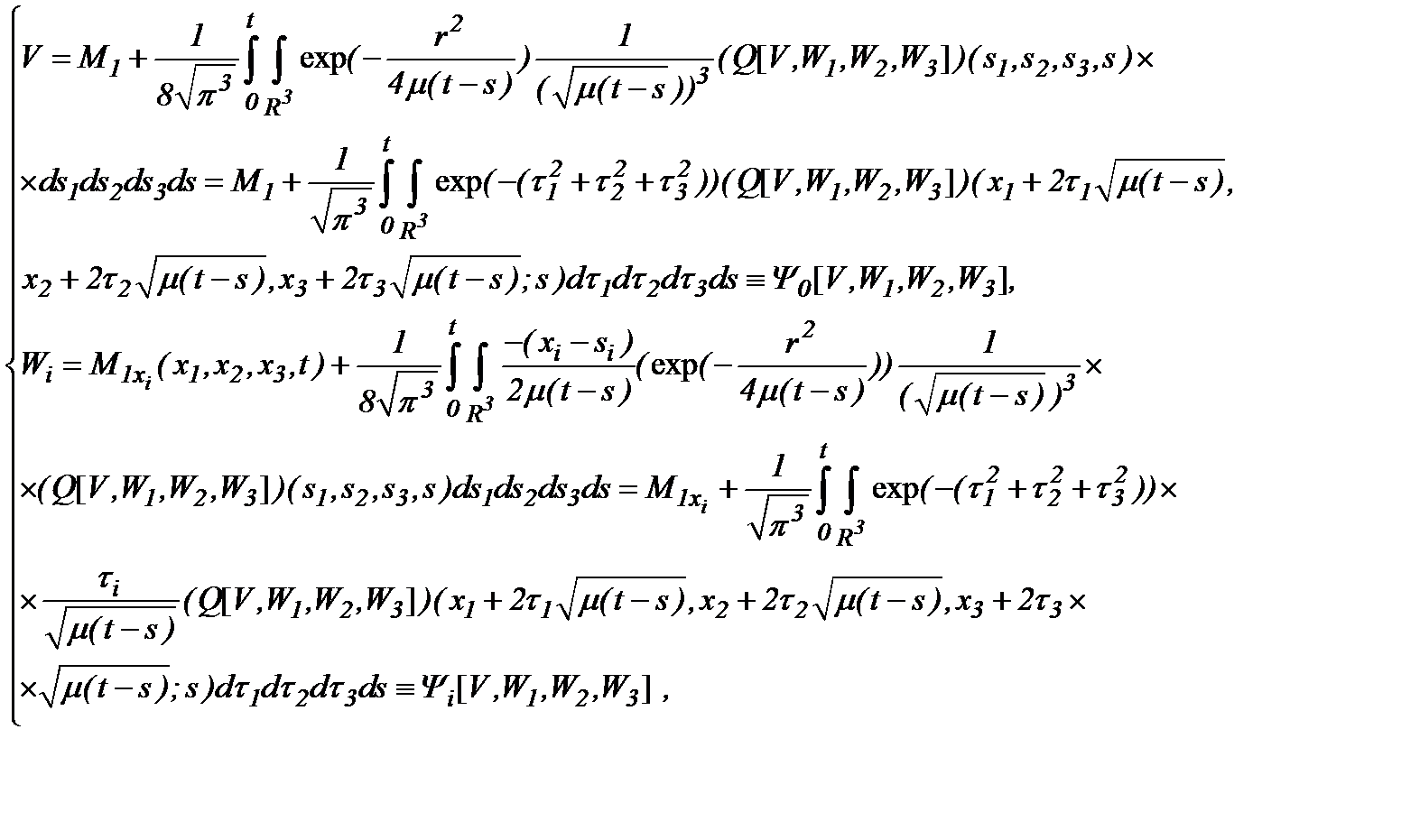 (4.42)
(4.42)
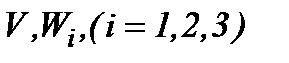 и состоит из четырех интегральных уравнений Вольтерра-Абеля второго рода по переменной
и состоит из четырех интегральных уравнений Вольтерра-Абеля второго рода по переменной 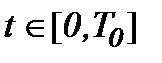 .
.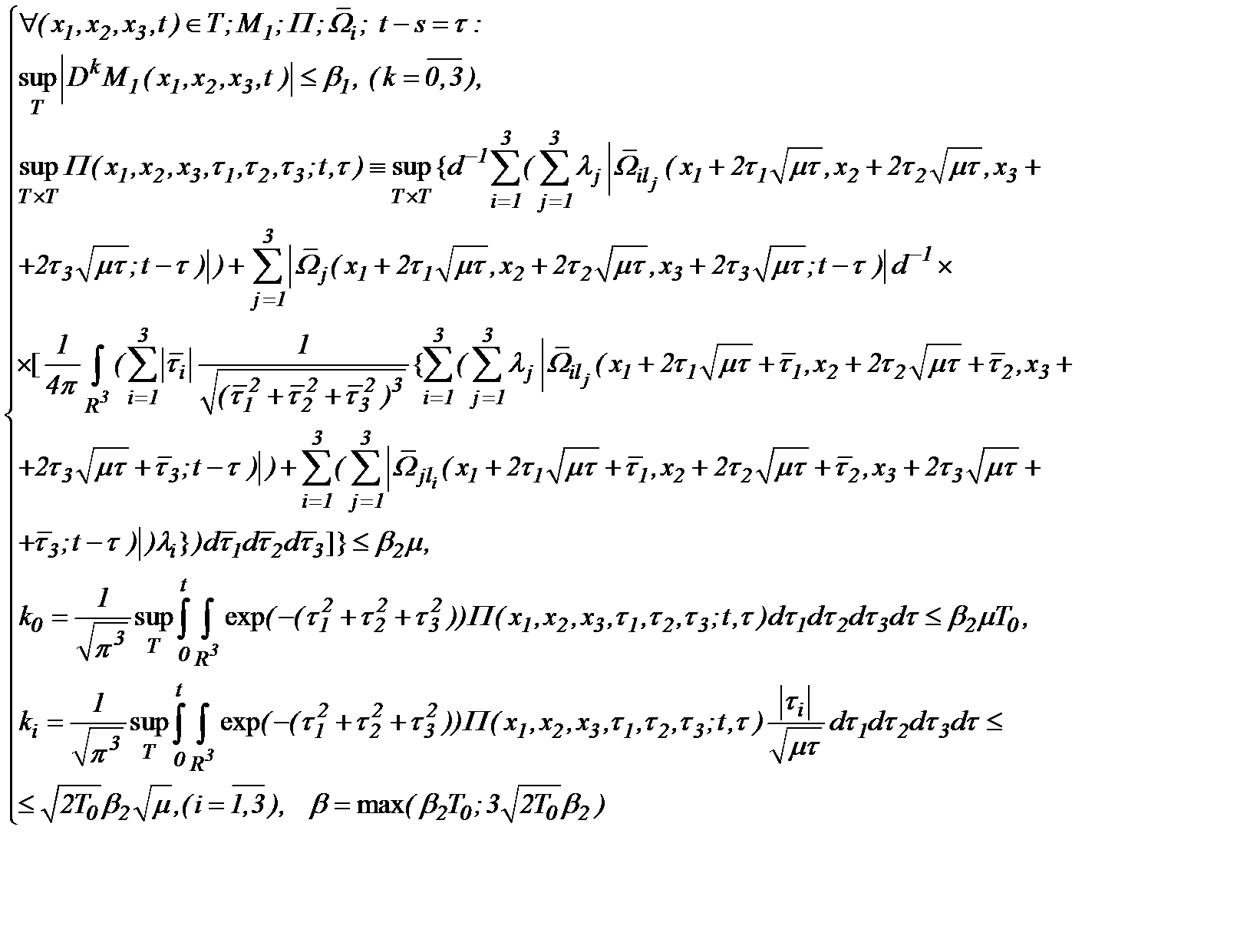 (4.43)
(4.43)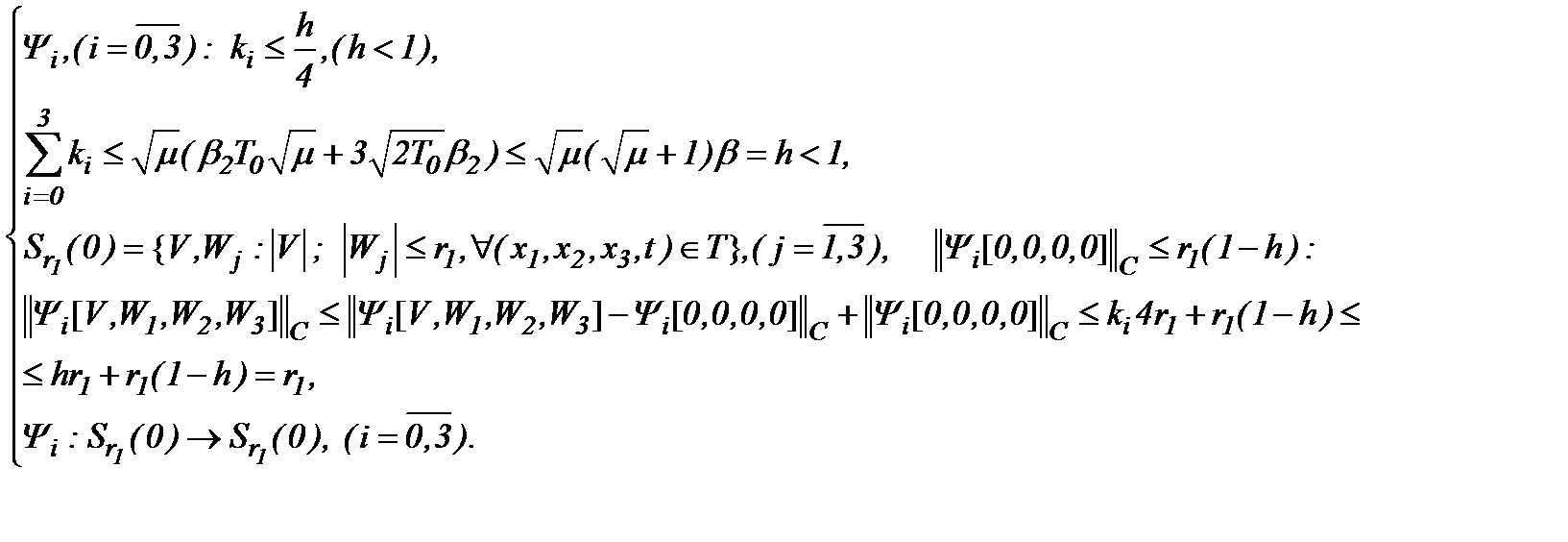 (4.44)
(4.44)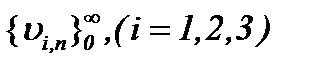 допускаются все выводы метода Пикара (4.31), указанные в предыдущих пунктах. Поэтому последовательность функций
допускаются все выводы метода Пикара (4.31), указанные в предыдущих пунктах. Поэтому последовательность функций 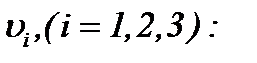
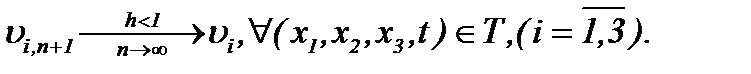 (4.45)
(4.45)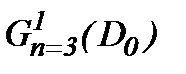 , так как
, так как 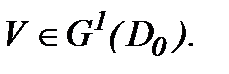 Поэтому результаты формулируются следующей теоремой.
Поэтому результаты формулируются следующей теоремой. 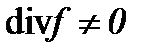 . В самом деле, если
. В самом деле, если 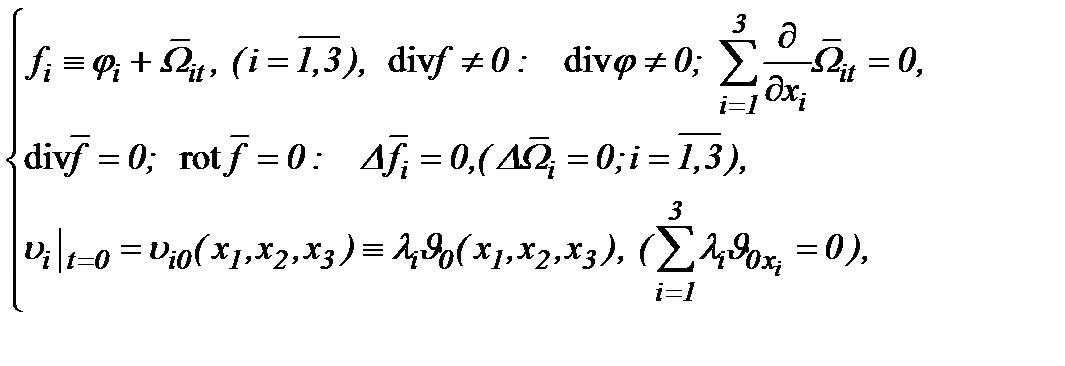 (4.46)
(4.46) 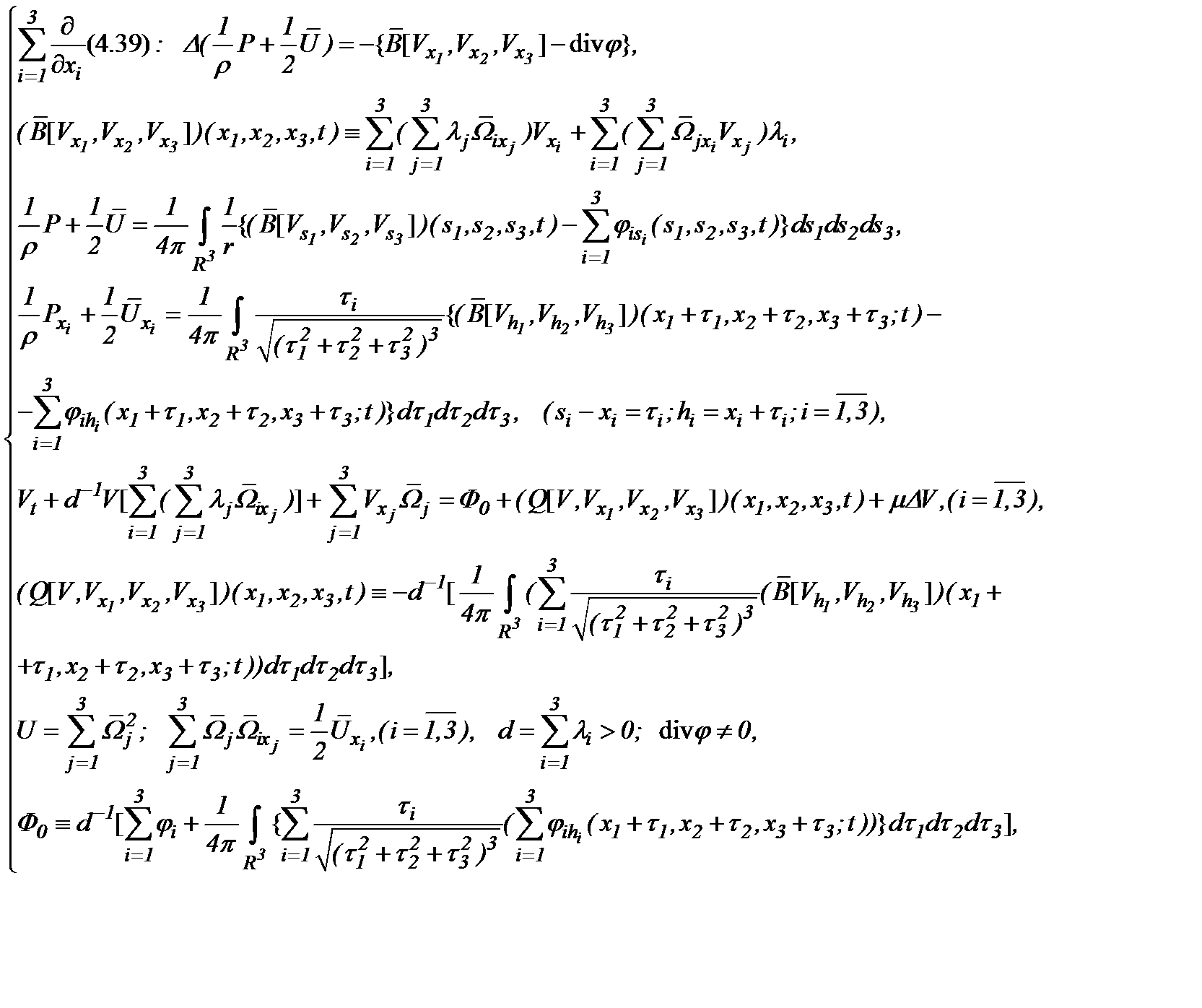
 (4.42)*
(4.42)*

