7. Жидкость с Вязкостью, Когда 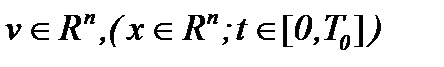
В этом параграфе покажем, что определенные математические преобразования эквивалентно трансформируют уравнения Навье-Стокса в линейные уравнения в случае 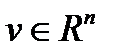 . Тем самым, удостоверившись, что решения в строго аналитической форме или решения, основанные на методе Пикара, имеют место не только для 3D уравнений Навье-Стокса с вязкостью [1], докажем, что и для nD уравнений Навье-Стокса имеют аналогичные решения в
. Тем самым, удостоверившись, что решения в строго аналитической форме или решения, основанные на методе Пикара, имеют место не только для 3D уравнений Навье-Стокса с вязкостью [1], докажем, что и для nD уравнений Навье-Стокса имеют аналогичные решения в 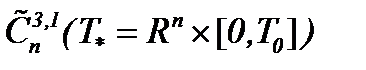 или
или 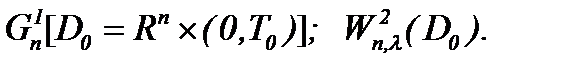
Предложенные в параграфе 4 методы интегральных преобразований были основаны на интегралах вольтерровского типа по переменной 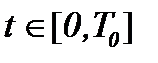 , когда
, когда 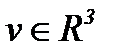 . Эти методы были введены так, чтобы превратить нелинейную задачу Навье-Стокса в линейную задачу теплопроводности с условием Коши. Наша цель заключается в развитии указанных методов для уравнений Навье-Стокса в многомерном случае, а именно
. Эти методы были введены так, чтобы превратить нелинейную задачу Навье-Стокса в линейную задачу теплопроводности с условием Коши. Наша цель заключается в развитии указанных методов для уравнений Навье-Стокса в многомерном случае, а именно 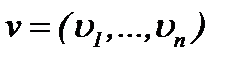 :
:
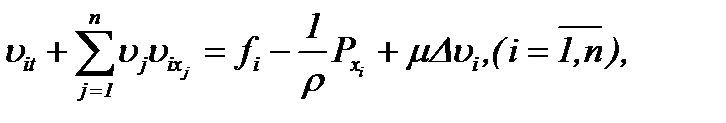 (1.1)n
(1.1)n
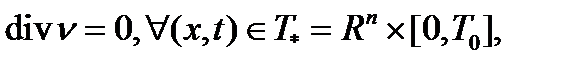 (1.2)n
(1.2)n
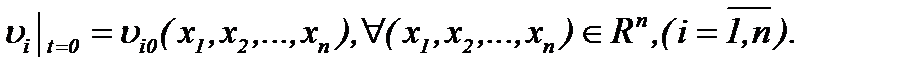 (1.3)n
(1.3)n
При условиях (1.2)n и (1.3)n система Навье-Стокса (1.1)n может иметь или аналитическое гладкое и единственное решение в 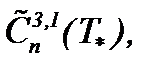 или условно-гладкое единственное решение в
или условно-гладкое единственное решение в 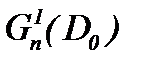 , в чем убедимся на самом деле.
, в чем убедимся на самом деле.
7.1. Жидкость с вязкостью 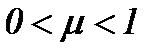 , когда
, когда 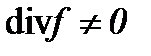
Пусть 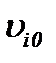 начальные компоненты вектора скорости
начальные компоненты вектора скорости 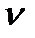 в момент времени
в момент времени 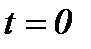 определяются, согласно (1.3)n, следующим образом
определяются, согласно (1.3)n, следующим образом
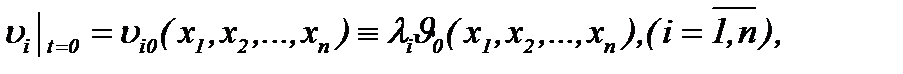 (7.1)
(7.1)
где 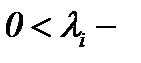 известные константы. Поэтому относительно компоненты скорости
известные константы. Поэтому относительно компоненты скорости 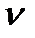 можем ввести формулу
можем ввести формулу
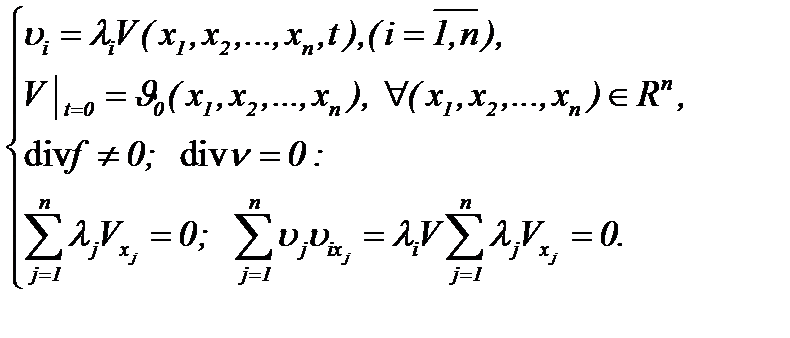 (7.2)
(7.2)
Тогда замена (7.2) эквивалентно превратит уравнения (1.1)n в систему линейных неоднородных уравнений вида
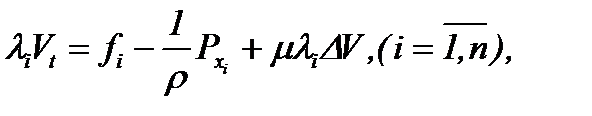 (7.3)
(7.3)
где 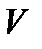 новая неизвестная функция, которая определяет решение задачи Навье-Стокса на основе формулы (7.2). Чтобы решить систему (7.3), в первую очередь, найдем давление
новая неизвестная функция, которая определяет решение задачи Навье-Стокса на основе формулы (7.2). Чтобы решить систему (7.3), в первую очередь, найдем давление 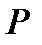 .
.
Действительно, применяя АПС, из системы (7.3) имеем
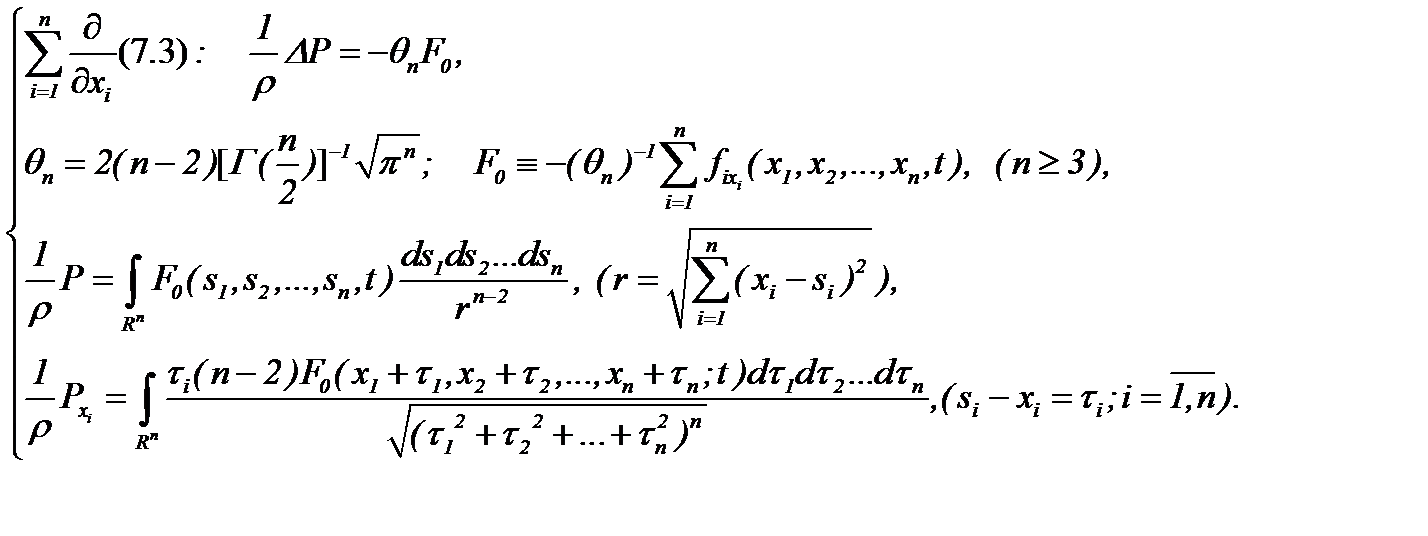 (7.4)
(7.4)
Следовательно, получили
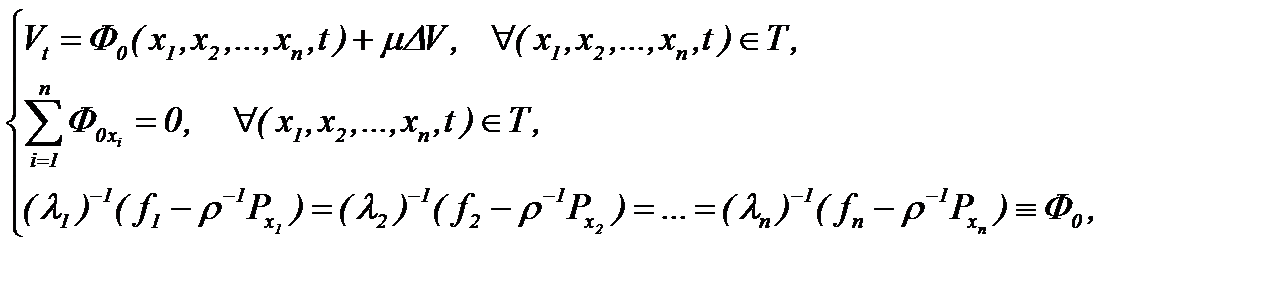 (7.5)
(7.5)
а это означает, что система (7.3) преобразована в линейное уравнение теплопроводности с условием Коши вида (7.5), которая разрешима в классе функций с достаточно гладкими начальными данными,
а потому существует условно-гладкое и единственное решение задачи Навье-Стокса в 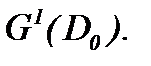
Действительно, из системы (7.5) следует
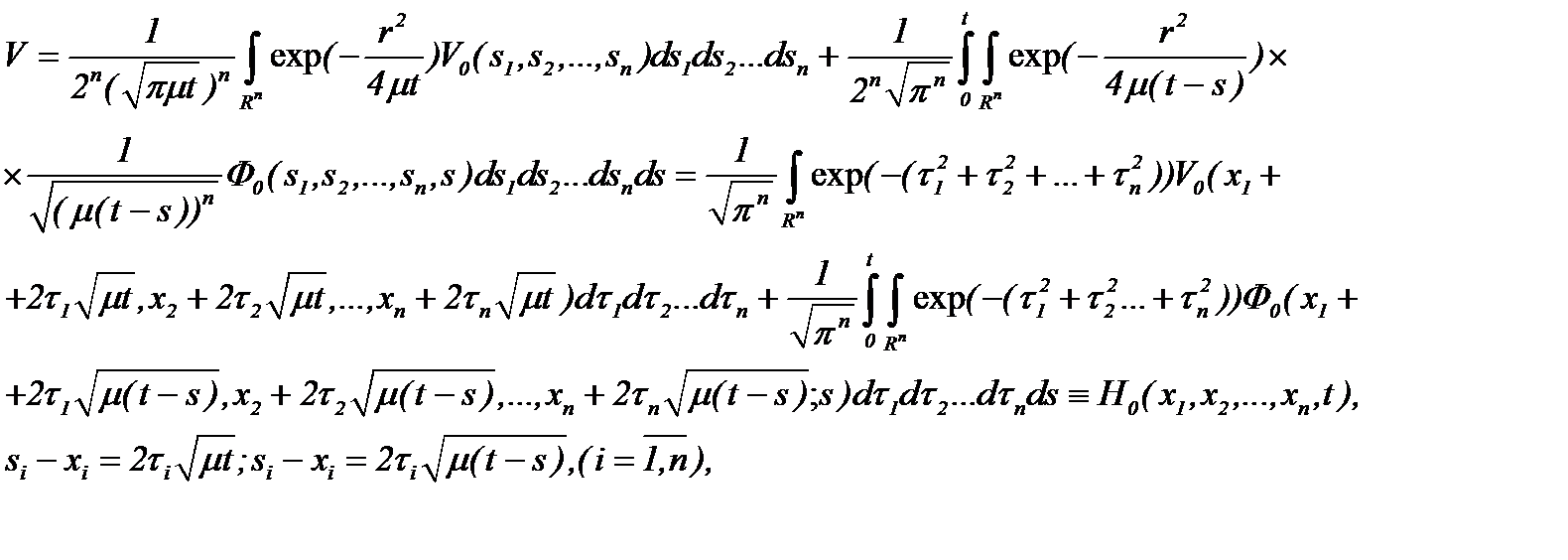 (7.6)
(7.6)
где 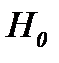 – известная функция. Для доказательства ограниченности решения (7.5) в
– известная функция. Для доказательства ограниченности решения (7.5) в 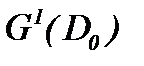 , как видно, решение (7.5) сведено к виду (7.6), когда
, как видно, решение (7.5) сведено к виду (7.6), когда
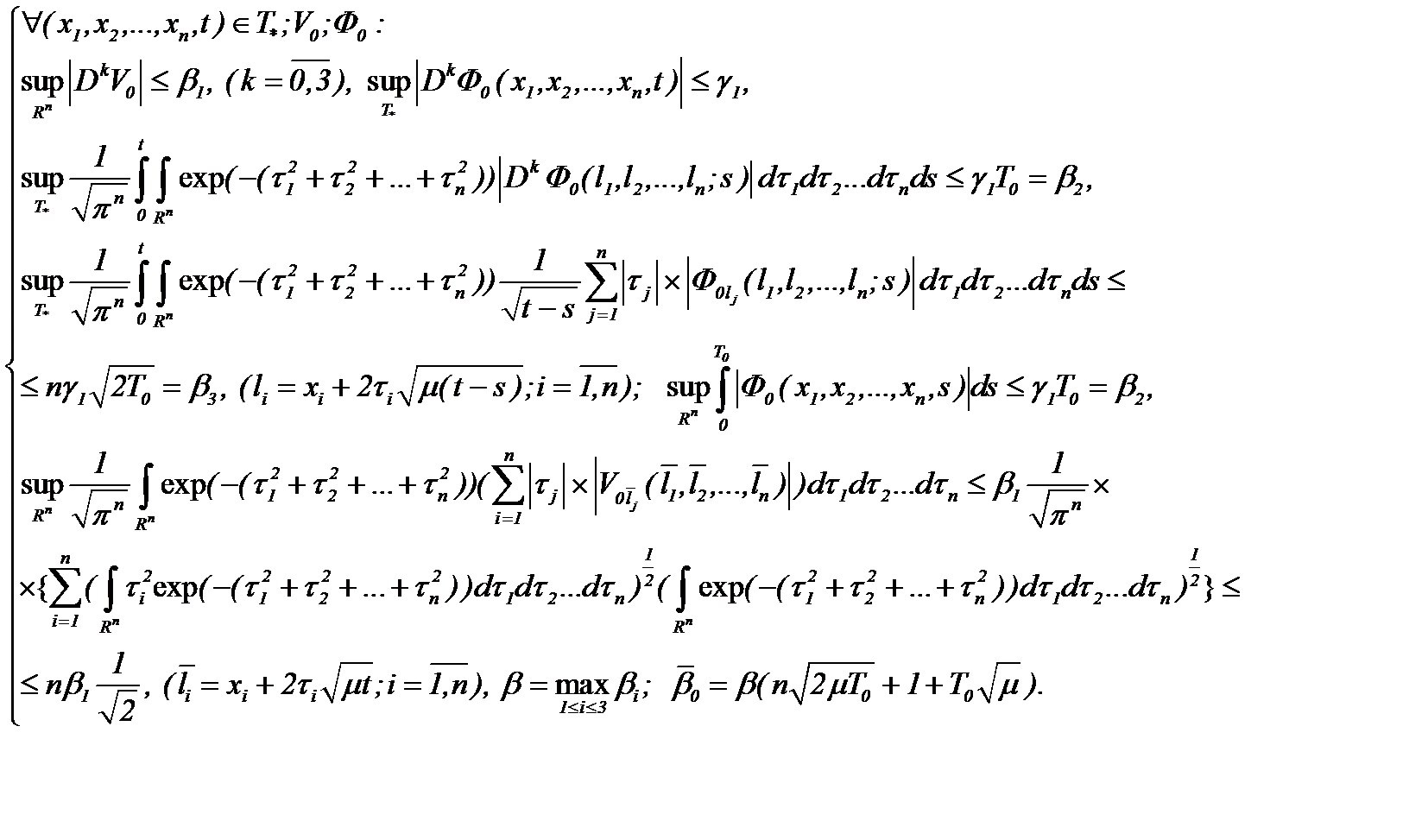 (7.7)
(7.7)
Теперь, оценивая (7.6) при соблюдении условия (7.7) в 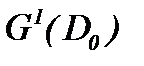 , имеем
, имеем
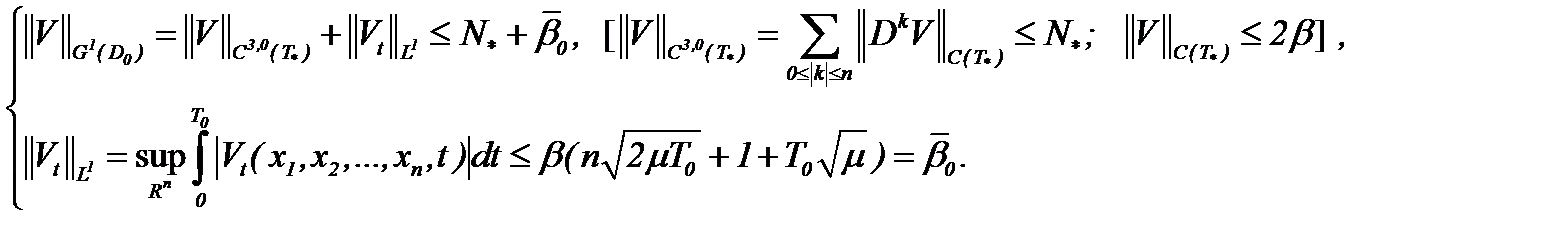 (7.8)
(7.8)
Единственность (7.6) в 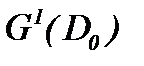 очевидна на основе метода от противного. Результаты (7.6) с
очевидна на основе метода от противного. Результаты (7.6) с
условием (7.2), (7.7) получены, когда гладкость функций требуется только по 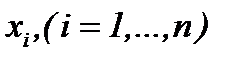 , а производная первого порядка по времени определяется для всех
, а производная первого порядка по времени определяется для всех 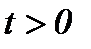 . Следовательно, на основе преобразования (7.2) получаем решения системы (1.1)n, которые удовлетворяют условию (1.2)n, т.е.
. Следовательно, на основе преобразования (7.2) получаем решения системы (1.1)n, которые удовлетворяют условию (1.2)n, т.е.
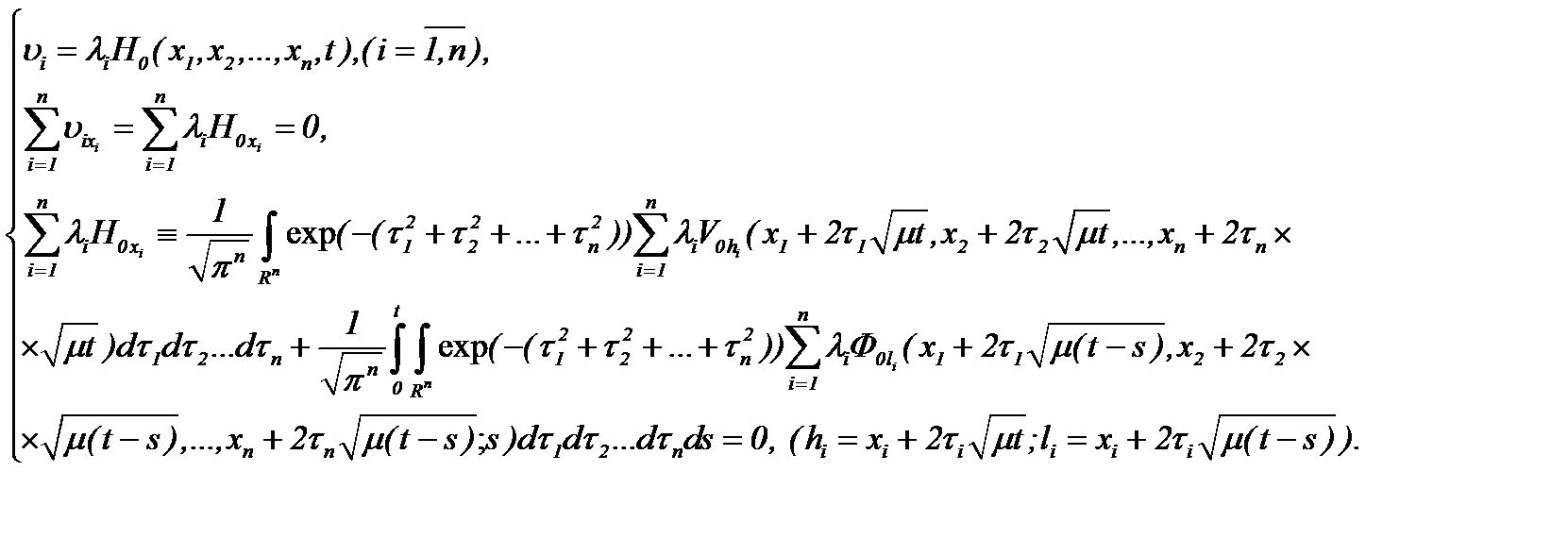 (7.9)
(7.9)
Наконец, с учетом нормы пространства 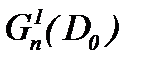 получим оценку решения (7.9):
получим оценку решения (7.9):
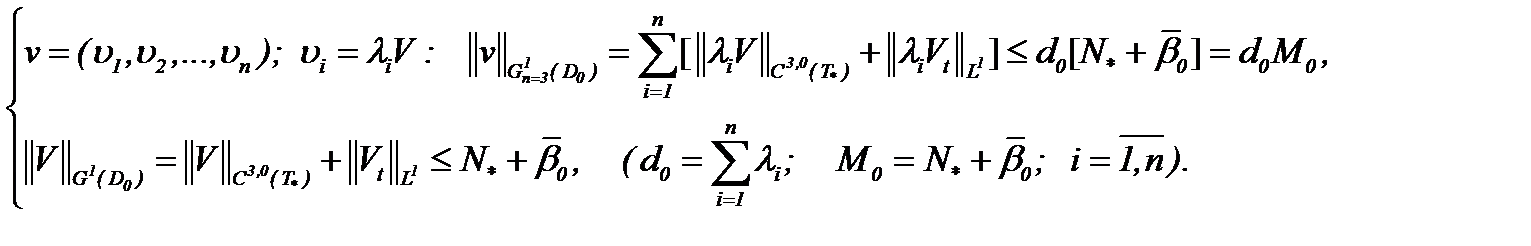 (7.10)
(7.10)
Следовательно, полученные результаты формулируются следующей теоремой.
Теорема 8. Задача (1.1)n, (1.2)n, (7.1) при условиях (1.2)n, (7.1), (7.7) и (7.10) имеет единственное решение в 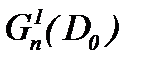 , которое определяется правилом (7.9).
, которое определяется правилом (7.9).
Замечание 7. Известно, что турбулентное решение обладает свойством условной гладкости в аналитическом смысле [4]. Поэтому, полагаем, что класс подходящих решений задачи Навье-Стокса является весовое пространство типа Соболева 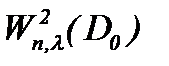 . Так как
. Так как 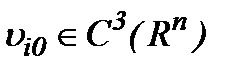 , то решение (7.6) задачи Навье-Стокса (1.1)n – (1.3)n принадлежит
, то решение (7.6) задачи Навье-Стокса (1.1)n – (1.3)n принадлежит 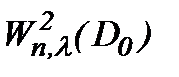 :
:
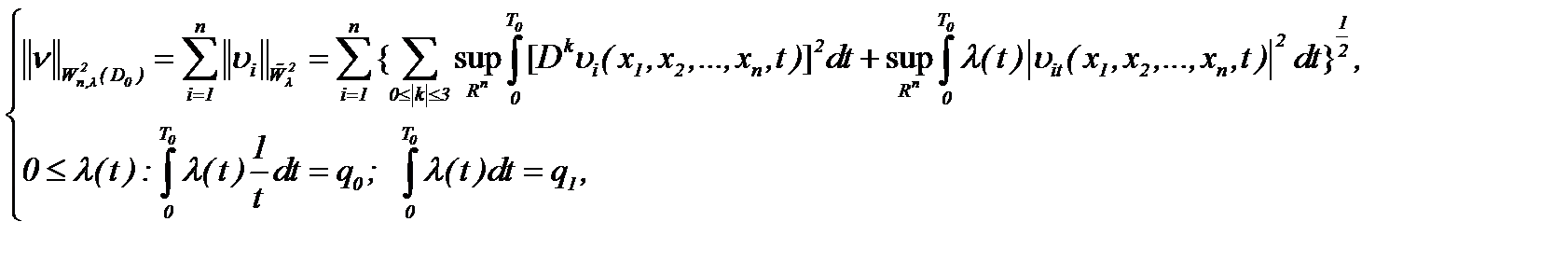
если имеет место
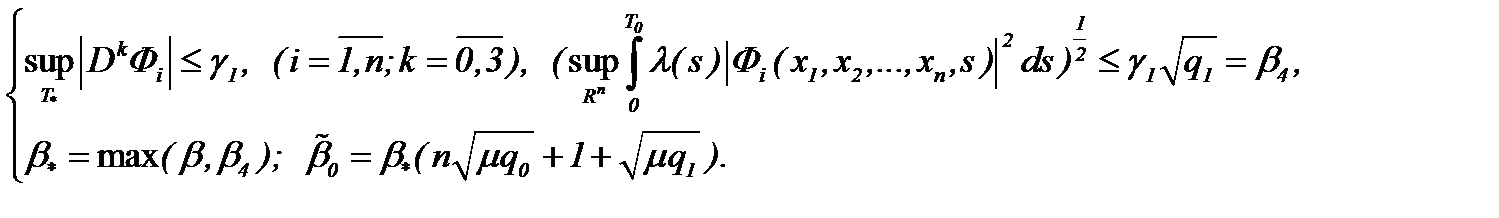 (7.11)
(7.11)
Для этого достаточно показать, что функция 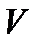 является элементом пространства
является элементом пространства 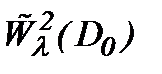 :
:
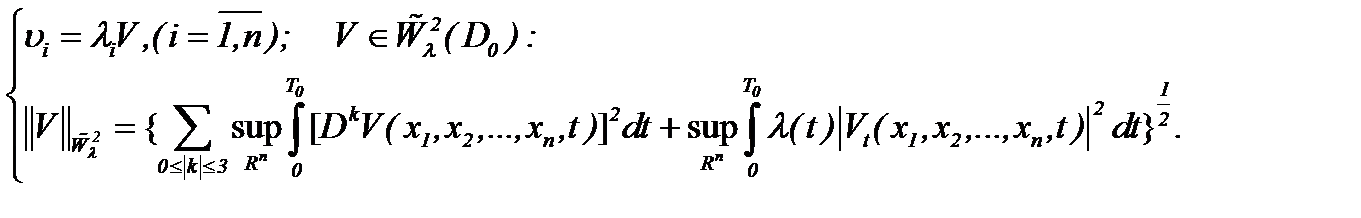
Пусть решение системы (7.5) представлено в виде (7.6) с условиями (7.7), (7.13). Тогда, проведя оценки (7.6) в 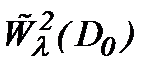 , получим
, получим
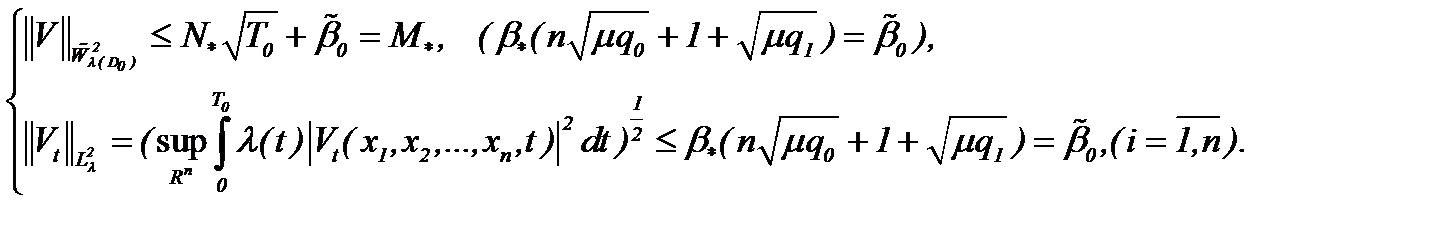 (7.12)
(7.12)
Значит, на основании (7.12), оценивая (7.2) в смысле нормы пространства 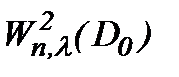 , имеем
, имеем
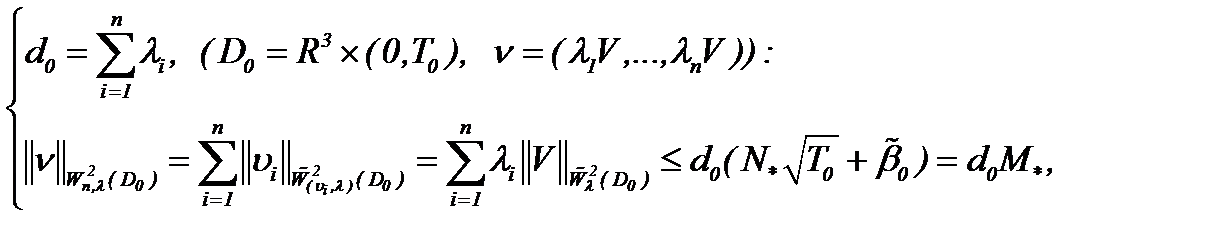
а это означает, что задача (1.1)n – (1.3)n при условиях (1.2)n, (1.3)n, (7.1), (7.7) и (7.11) имеет строгое и условно-гладкое решение в 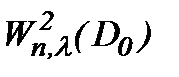 , что и требовалось доказать.
, что и требовалось доказать.
7.2. Жидкость с вязкостью 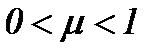 , когда
, когда 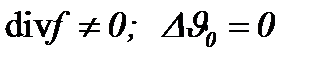
I . Целью пункта является модификация метода (7.2), необходимая, чтобы получить аналитическое решение задачи Навье-Стокса с вязкостью, принадлежащее 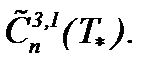
Поскольку имеем
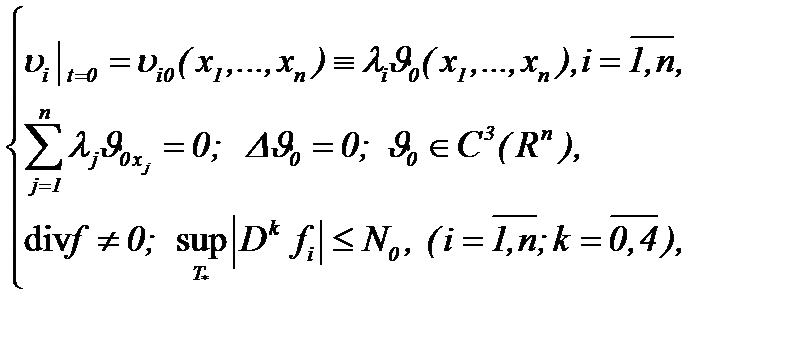 (7.13)
(7.13)
то применим преобразование
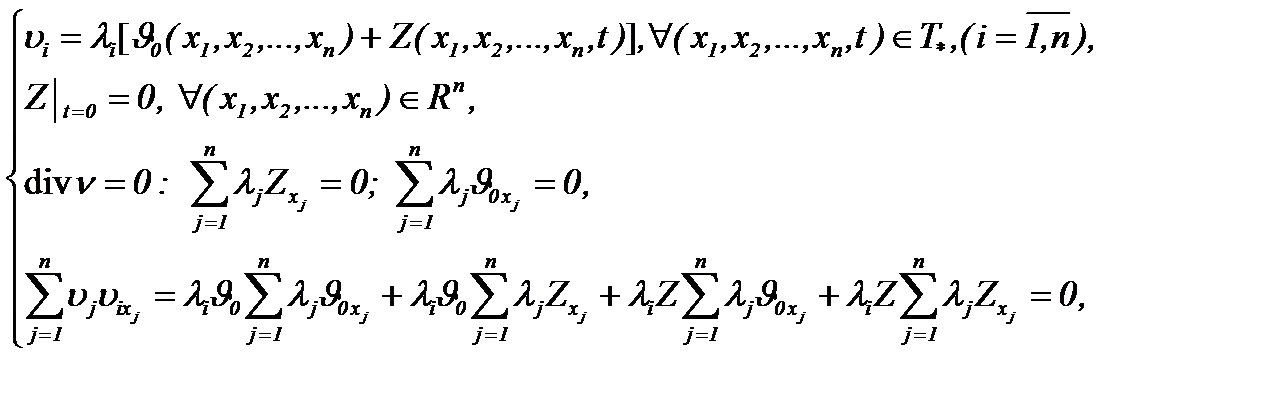 (7.14)
(7.14)
где 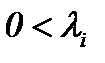 – известные константы. Тогда система (1.1)n трансформируется к виду
– известные константы. Тогда система (1.1)n трансформируется к виду
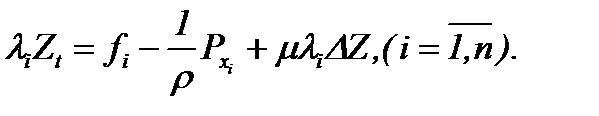 (7.15)
(7.15)
Из системы (7.15), учитывая условия (7.13), (7.14) и применяя АПС, получим уравнение (7.4).
Таким образом, на основе (7.4) вместо уравнения (7.15) имеем линейное неоднородное дифференциальное уравнение с условием Коши
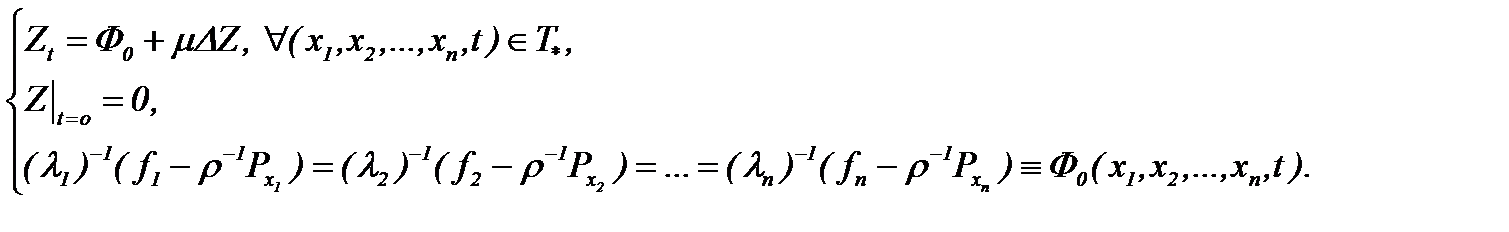 (7.16)
(7.16)
Тогда решение задачи (7.16) представимо в виде
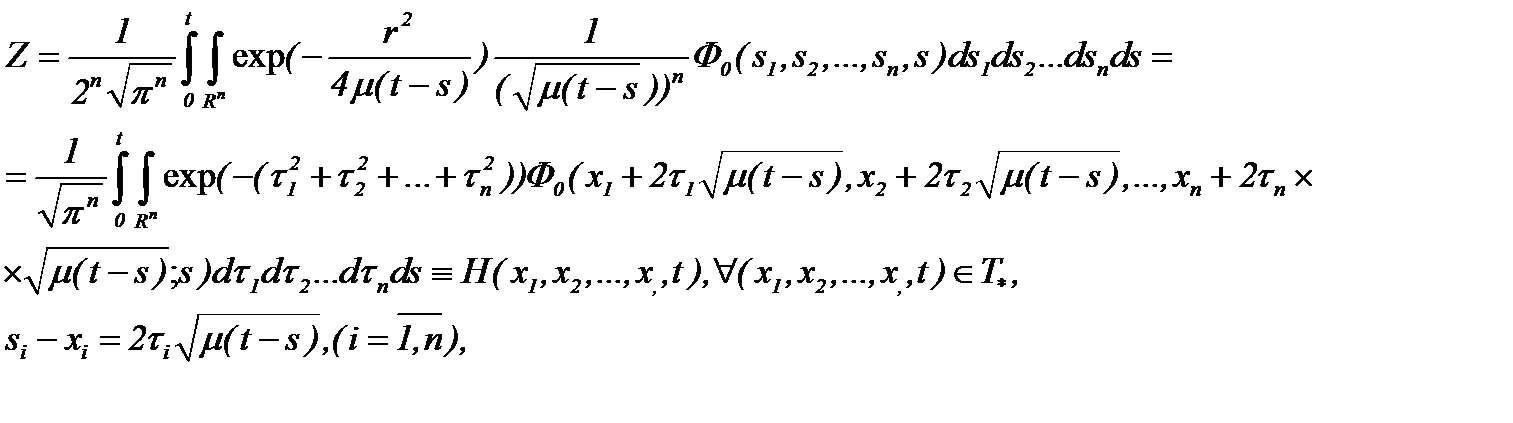 (7.17)
(7.17)
где H – известная функция. Найденное решение (7.17) удовлетворяет уравнению (7.16).
Действительно, рассчитав частные производные системы (7.17)
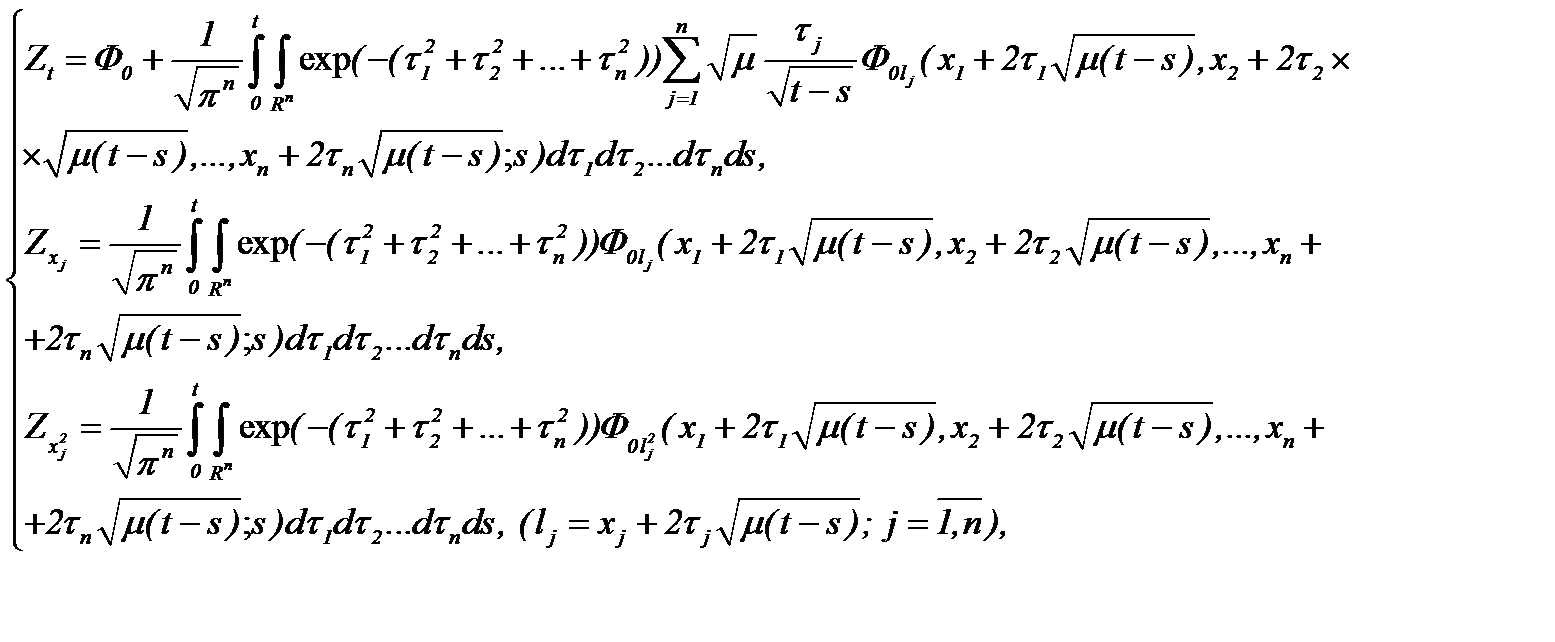 (7.18)
(7.18)
а, затем, подставляя (7.18) в (7.16), имеем
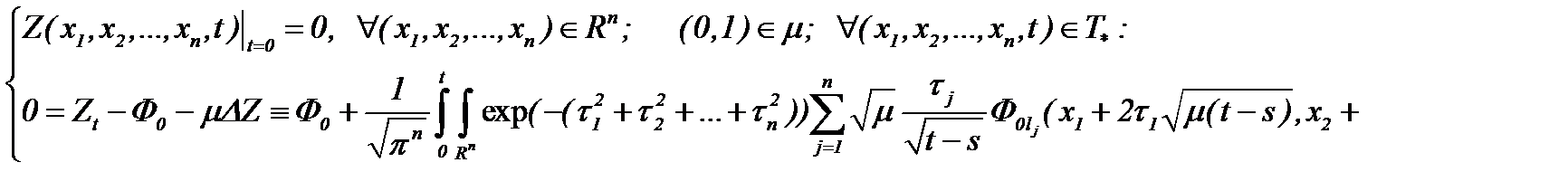
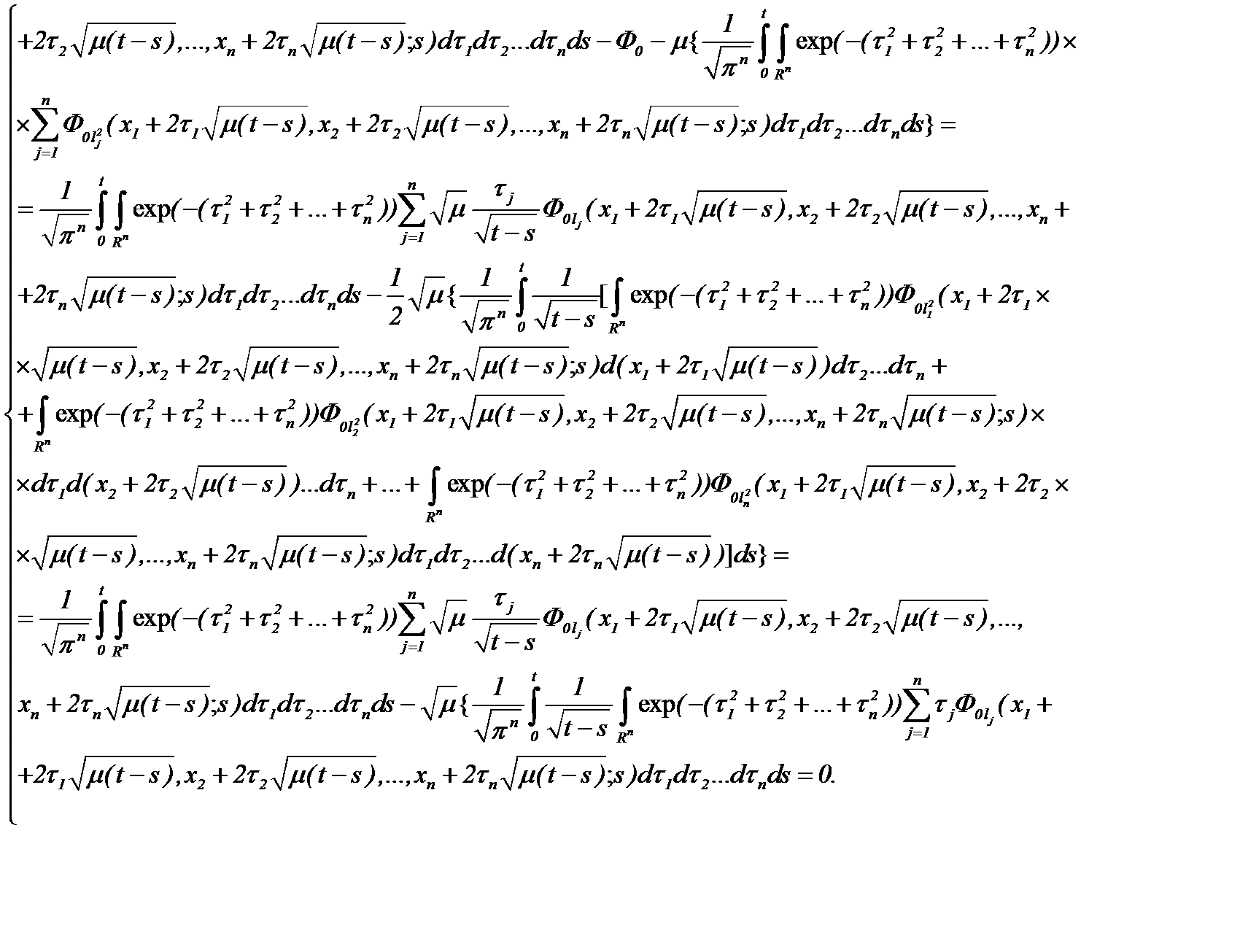
Таким образом, получено то, что и требовалось доказать.
Из полученных результатов следует, что функции 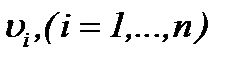 определяются на основе (7.14), а именно
определяются на основе (7.14), а именно
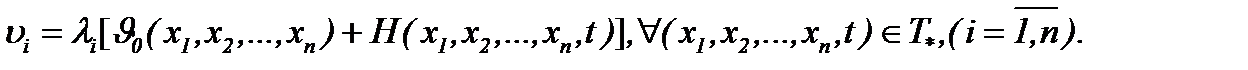 (7.19)
(7.19)
Кроме того, учитывая частные производные систем первого порядка (7.19), принимая во внимание (1.2)n и (7.14), а, затем, подводя итог, получим, что система (7.19) удовлетворяет условию (1.2)n:
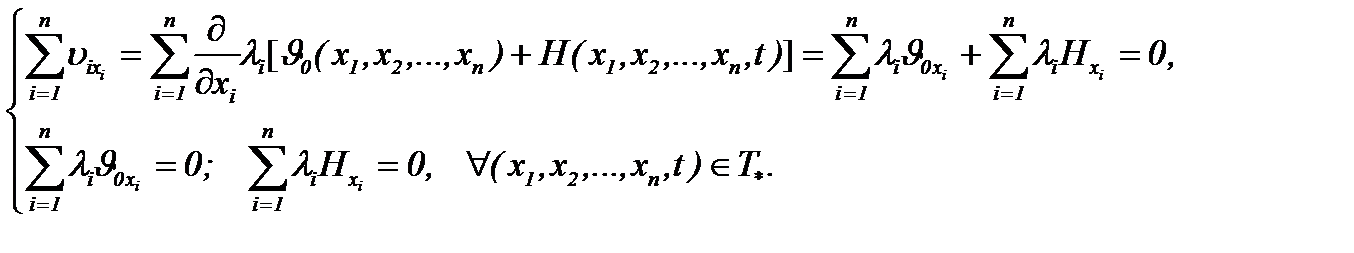
II . Так как 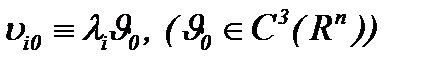 , то решение задачи (1.1)n – (1.3)n ограничено в
, то решение задачи (1.1)n – (1.3)n ограничено в 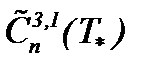 :
:
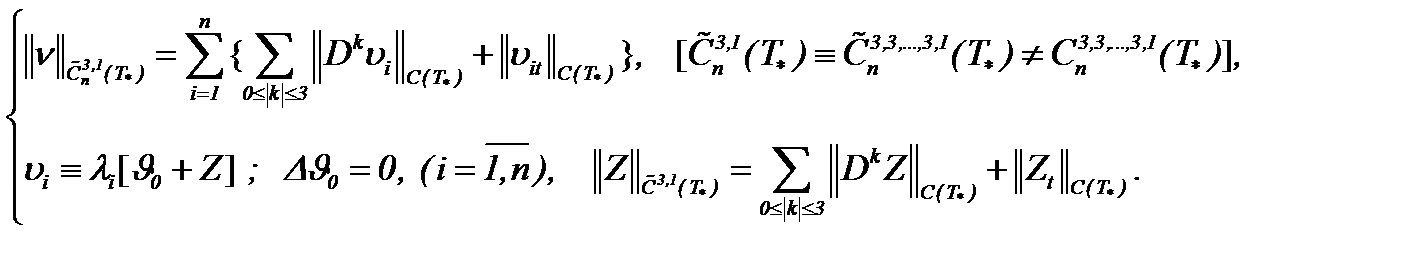
Действительно, если
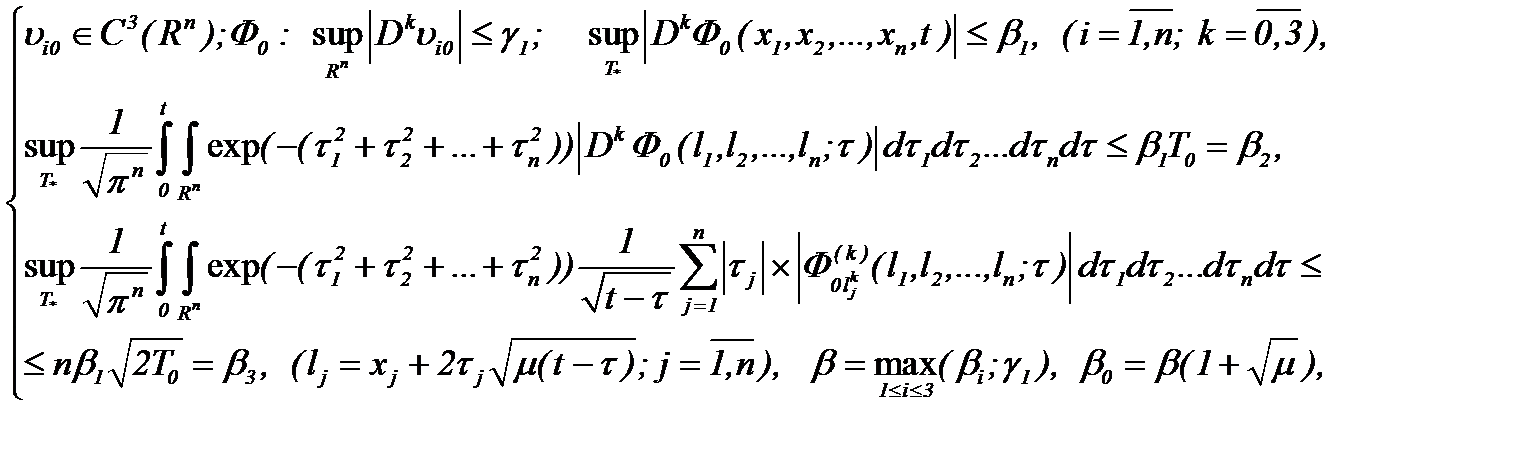 (7.20)
(7.20)
то на основе (7.17) получим
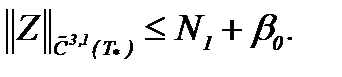
Наконец, оценивая (7.19) в смысле нормы пространства 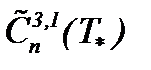 , имеем
, имеем
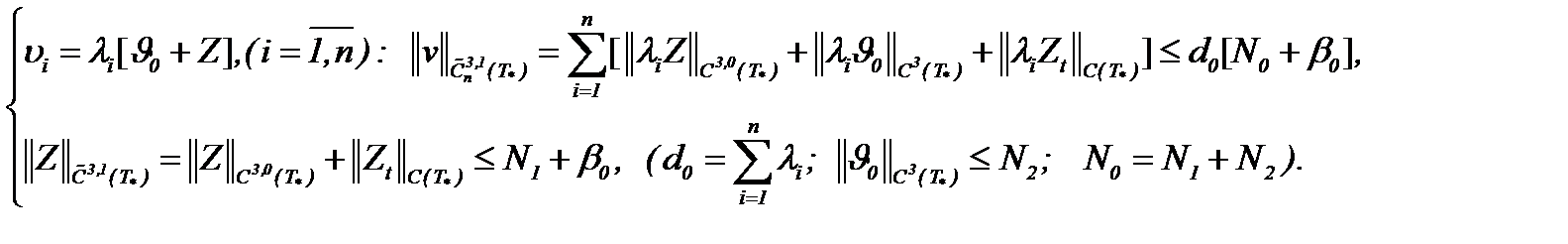
Лемма 3. При условиях (1.2)n, (7.13), (7.14) и (7.20) уравнение (7.17) имеет единственное решение в 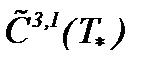 .
.
Теорема 8*. Задача (1.1)n, (1.2)n, (7.13) при выполнении условий леммы 3 разрешима в 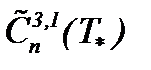 и решение определяется правилом (7.19).
и решение определяется правилом (7.19).
Итогом исследований настоящего пункта являются результаты теоремы 8*, на основании которых решение системы (1.1)n является строго аналитическим и единственным решением задачи (1.1)n – (1.3)n в 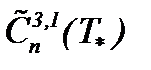 . Поэтому корректность постановки задачи (1.1)n – (1.3)n разрешается, исходя из результатов теоремы 8*.
. Поэтому корректность постановки задачи (1.1)n – (1.3)n разрешается, исходя из результатов теоремы 8*.





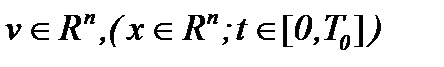
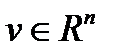 . Тем самым, удостоверившись, что решения в строго аналитической форме или решения, основанные на методе Пикара, имеют место не только для 3D уравнений Навье-Стокса с вязкостью [1], докажем, что и для nD уравнений Навье-Стокса имеют аналогичные решения в
. Тем самым, удостоверившись, что решения в строго аналитической форме или решения, основанные на методе Пикара, имеют место не только для 3D уравнений Навье-Стокса с вязкостью [1], докажем, что и для nD уравнений Навье-Стокса имеют аналогичные решения в 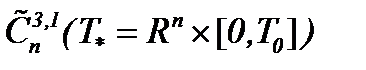 или
или 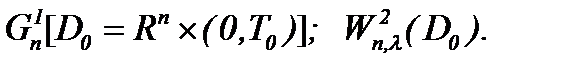
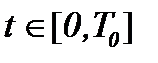 , когда
, когда 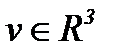 . Эти методы были введены так, чтобы превратить нелинейную задачу Навье-Стокса в линейную задачу теплопроводности с условием Коши. Наша цель заключается в развитии указанных методов для уравнений Навье-Стокса в многомерном случае, а именно
. Эти методы были введены так, чтобы превратить нелинейную задачу Навье-Стокса в линейную задачу теплопроводности с условием Коши. Наша цель заключается в развитии указанных методов для уравнений Навье-Стокса в многомерном случае, а именно 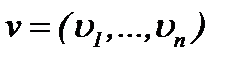 :
: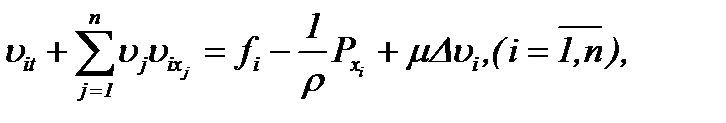 (1.1)n
(1.1)n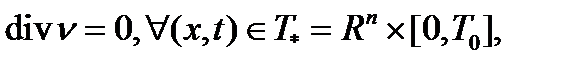 (1.2)n
(1.2)n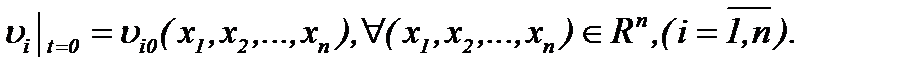 (1.3)n
(1.3)n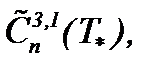 или условно-гладкое единственное решение в
или условно-гладкое единственное решение в 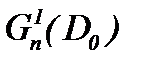 , в чем убедимся на самом деле.
, в чем убедимся на самом деле.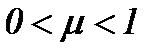 , когда
, когда 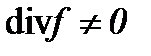
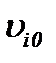 начальные компоненты вектора скорости
начальные компоненты вектора скорости 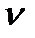 в момент времени
в момент времени 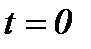 определяются, согласно (1.3)n, следующим образом
определяются, согласно (1.3)n, следующим образом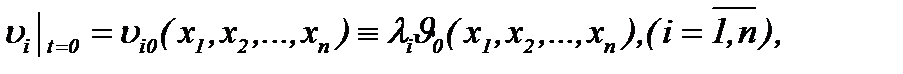 (7.1)
(7.1)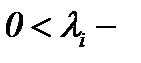 известные константы. Поэтому относительно компоненты скорости
известные константы. Поэтому относительно компоненты скорости 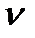 можем ввести формулу
можем ввести формулу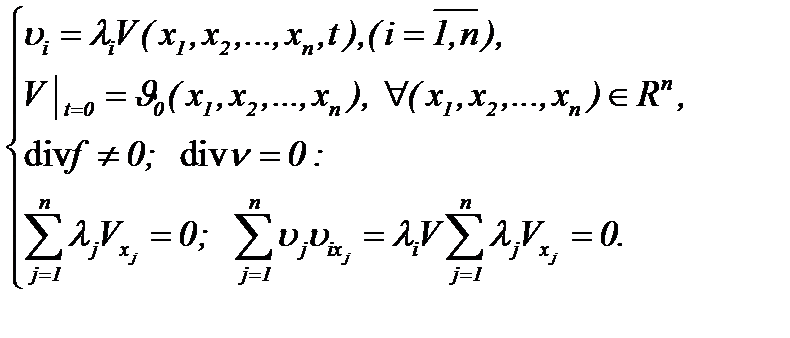 (7.2)
(7.2)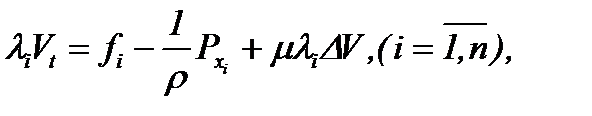 (7.3)
(7.3)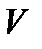 новая неизвестная функция, которая определяет решение задачи Навье-Стокса на основе формулы (7.2). Чтобы решить систему (7.3), в первую очередь, найдем давление
новая неизвестная функция, которая определяет решение задачи Навье-Стокса на основе формулы (7.2). Чтобы решить систему (7.3), в первую очередь, найдем давление 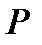 .
.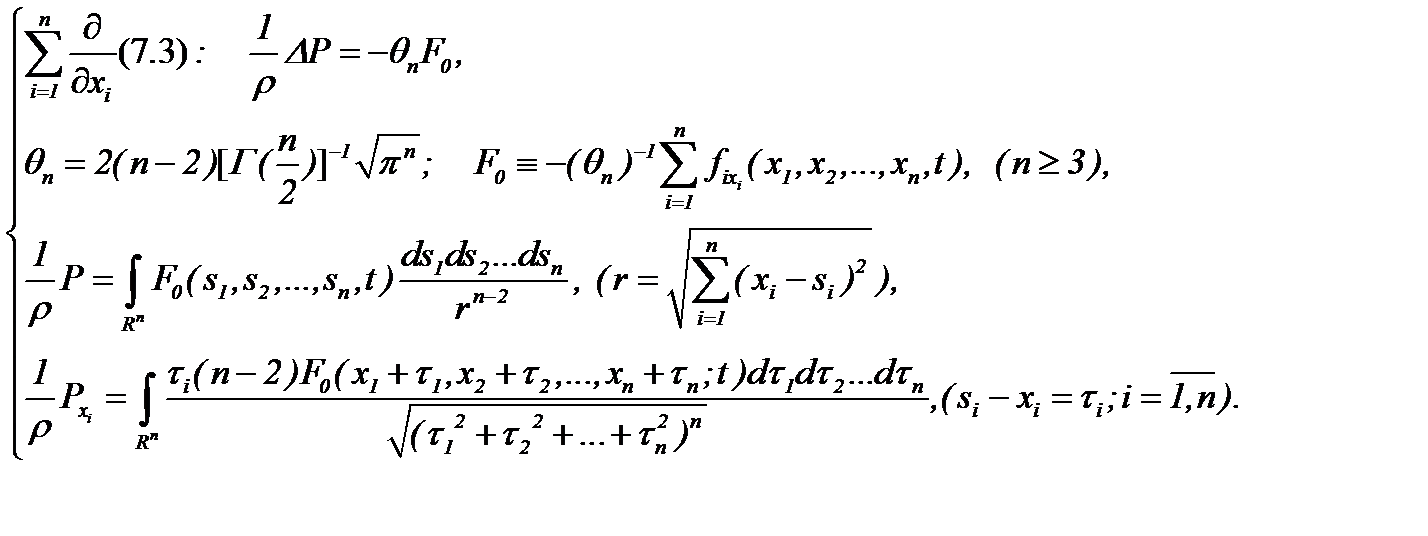 (7.4)
(7.4)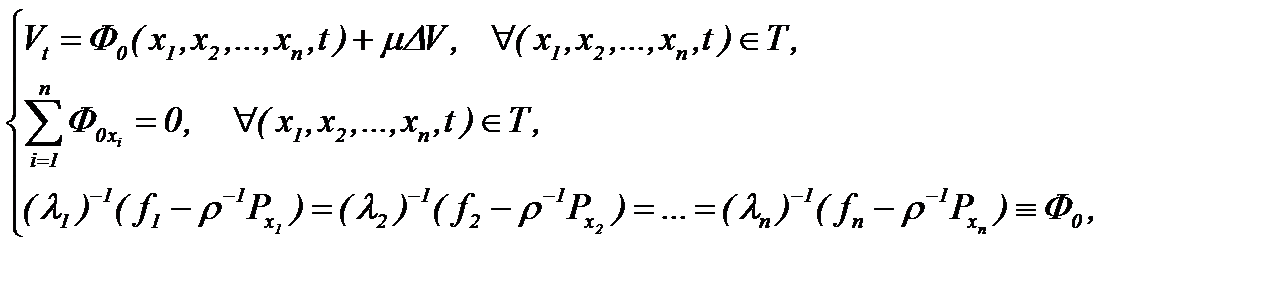 (7.5)
(7.5)
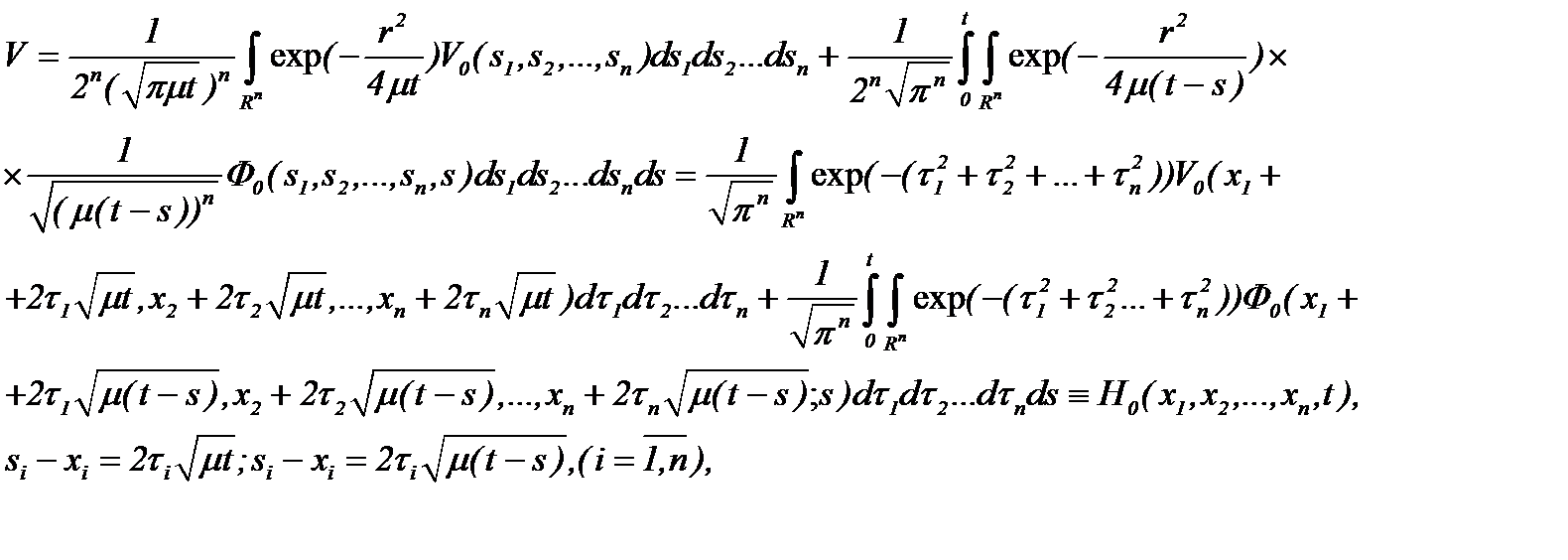 (7.6)
(7.6)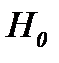 – известная функция. Для доказательства ограниченности решения (7.5) в
– известная функция. Для доказательства ограниченности решения (7.5) в 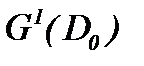 , как видно, решение (7.5) сведено к виду (7.6), когда
, как видно, решение (7.5) сведено к виду (7.6), когда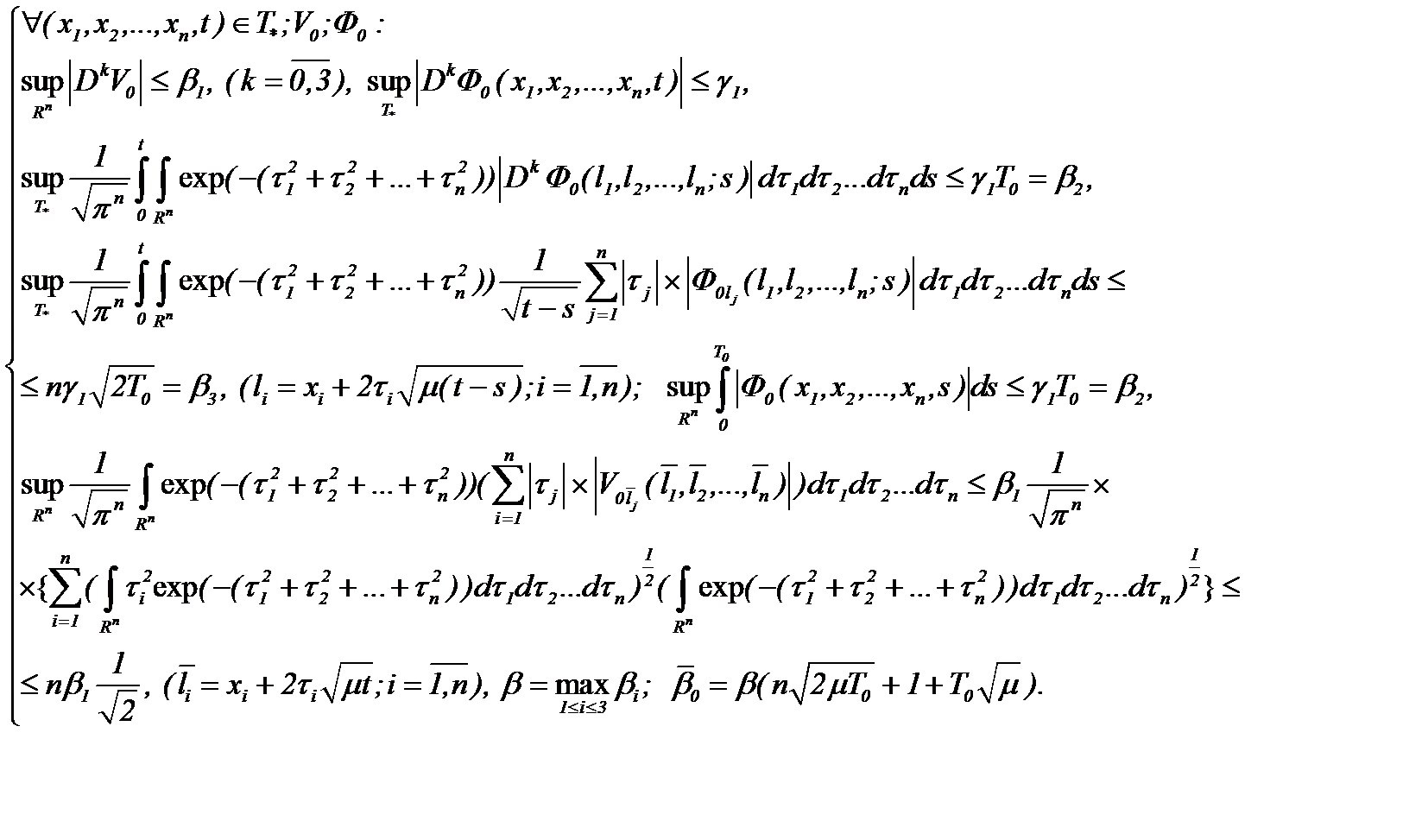 (7.7)
(7.7) 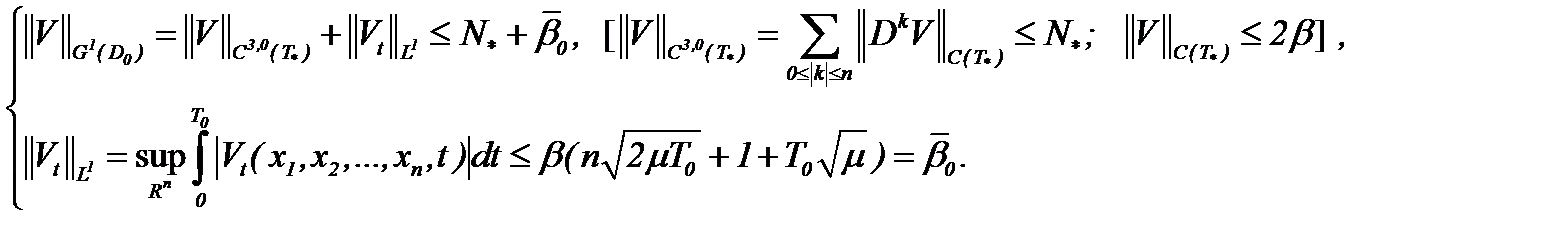 (7.8)
(7.8)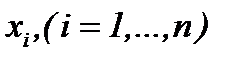 , а производная первого порядка по времени определяется для всех
, а производная первого порядка по времени определяется для всех 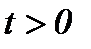 . Следовательно, на основе преобразования (7.2) получаем решения системы (1.1)n, которые удовлетворяют условию (1.2)n, т.е.
. Следовательно, на основе преобразования (7.2) получаем решения системы (1.1)n, которые удовлетворяют условию (1.2)n, т.е. 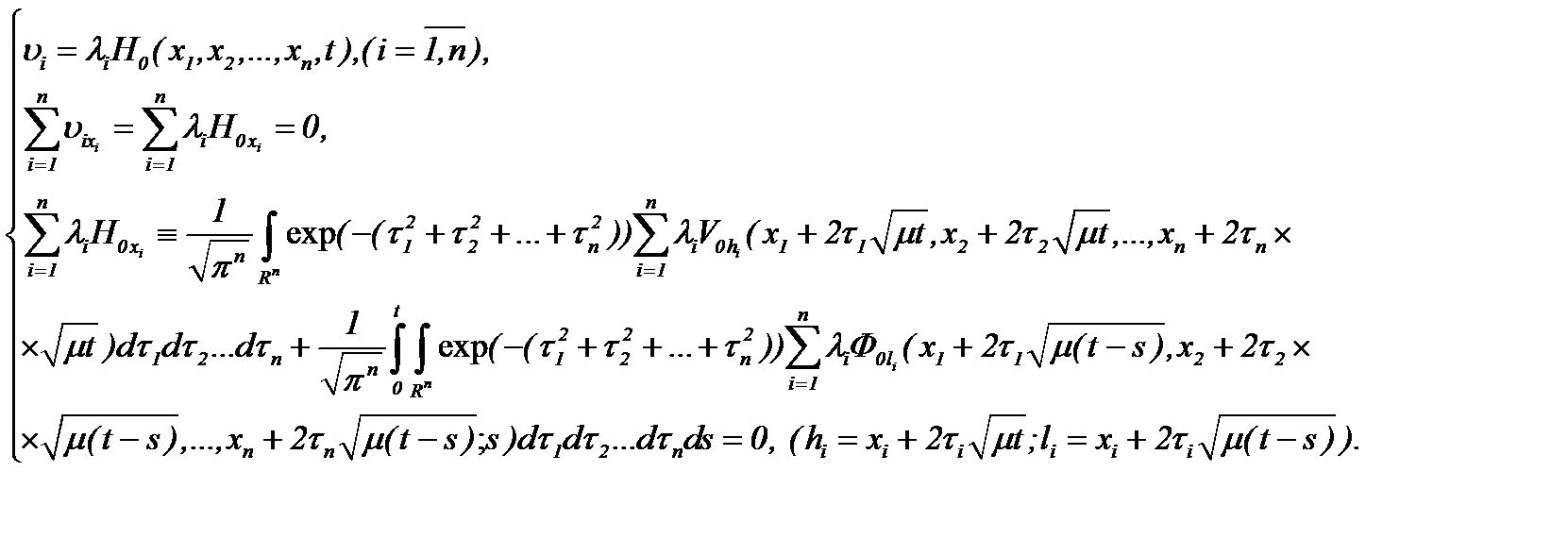 (7.9)
(7.9)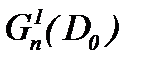 получим оценку решения (7.9):
получим оценку решения (7.9):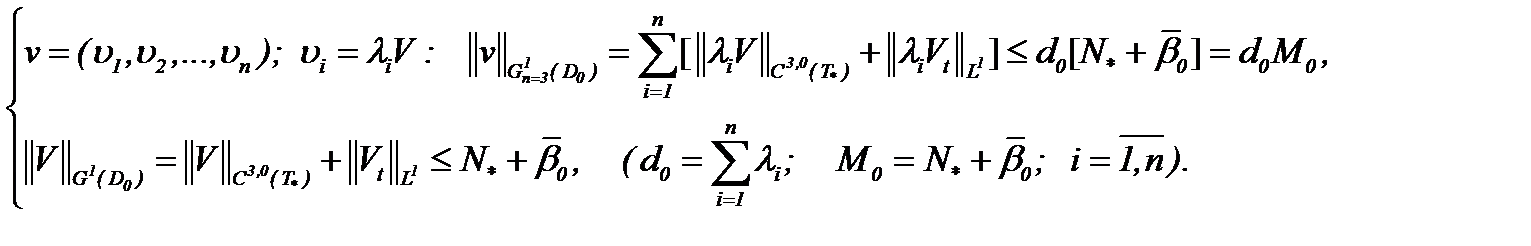 (7.10)
(7.10)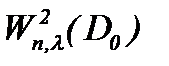 . Так как
. Так как 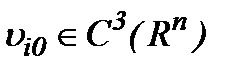 , то решение (7.6) задачи Навье-Стокса (1.1)n – (1.3)n принадлежит
, то решение (7.6) задачи Навье-Стокса (1.1)n – (1.3)n принадлежит 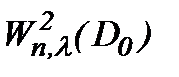 :
: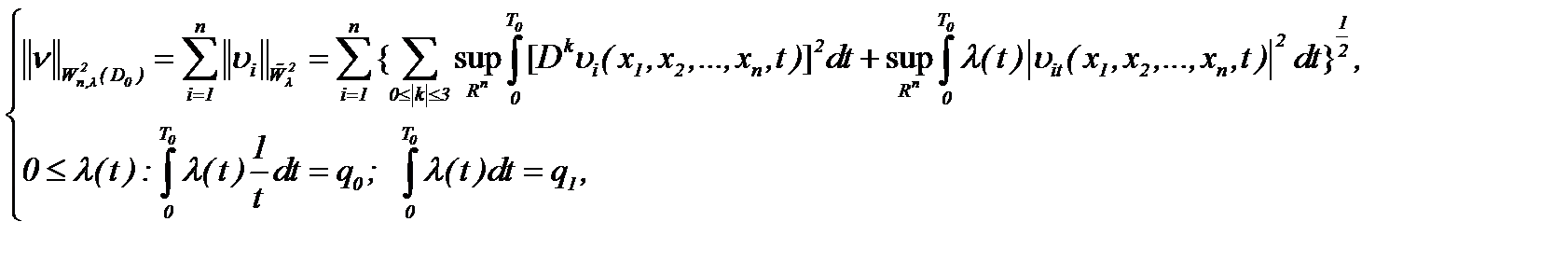
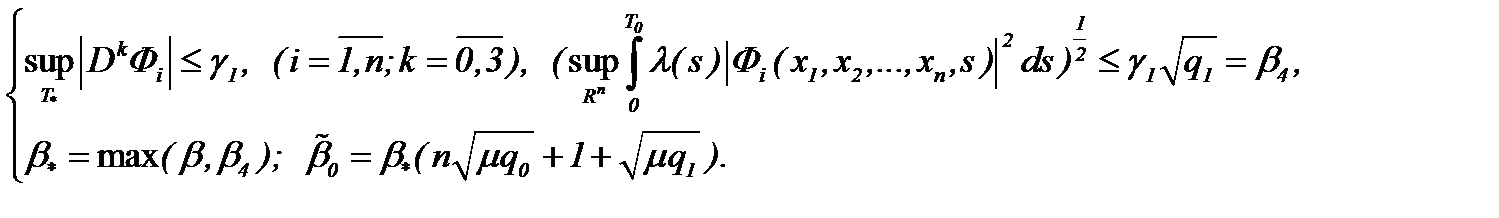 (7.11)
(7.11)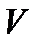 является элементом пространства
является элементом пространства 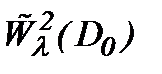 :
: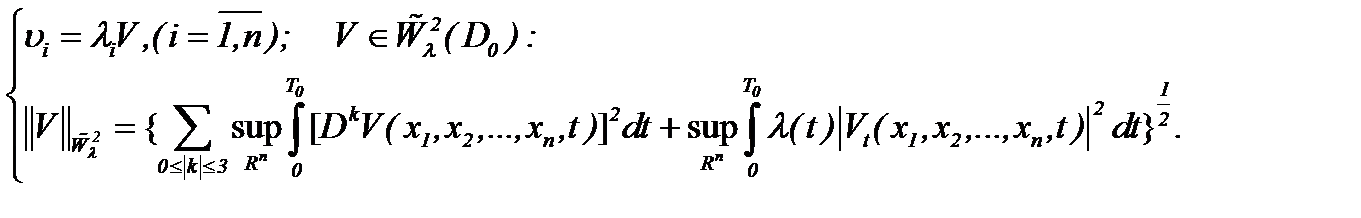
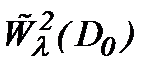 , получим
, получим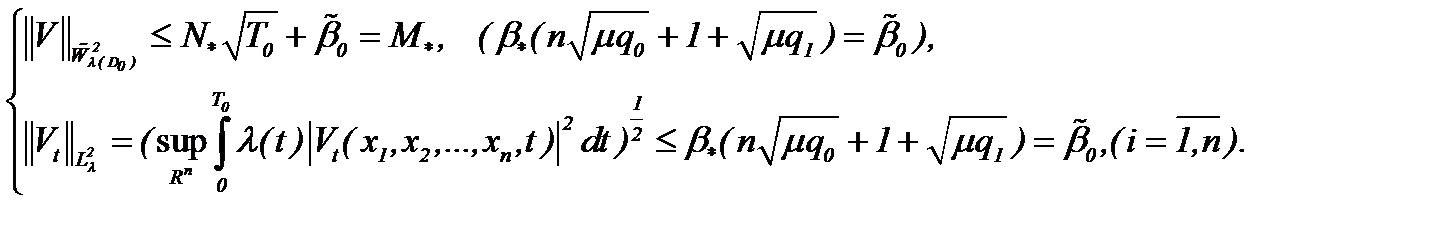 (7.12)
(7.12)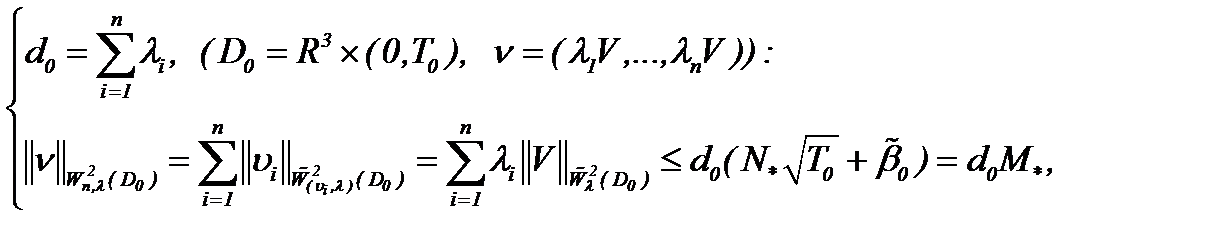
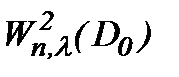 , что и требовалось доказать.
, что и требовалось доказать.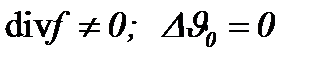
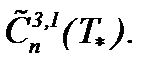
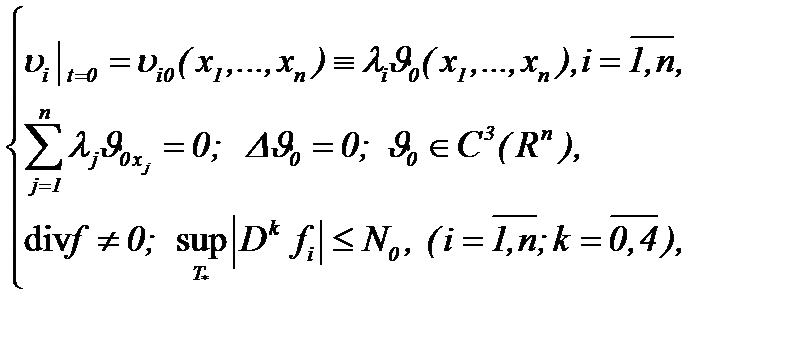 (7.13)
(7.13)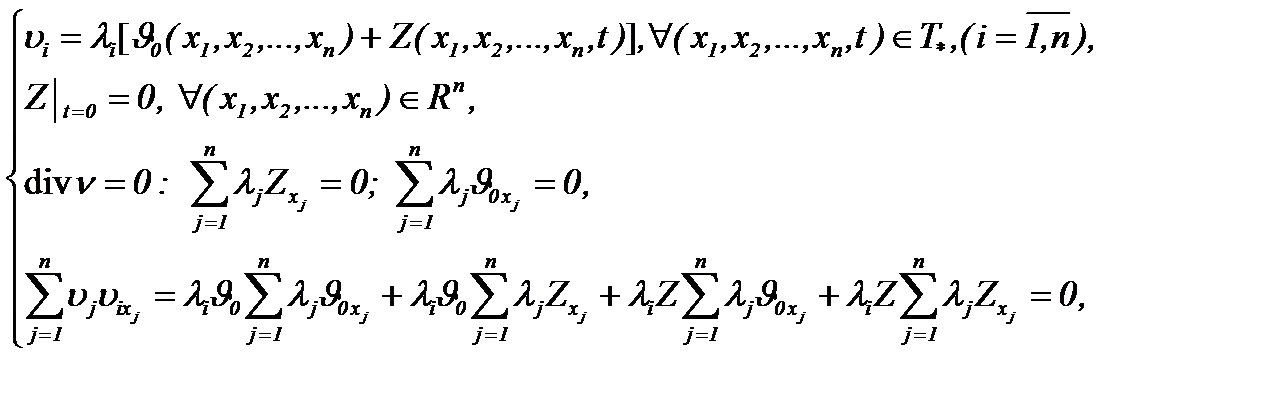 (7.14)
(7.14)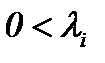 – известные константы. Тогда система (1.1)n трансформируется к виду
– известные константы. Тогда система (1.1)n трансформируется к виду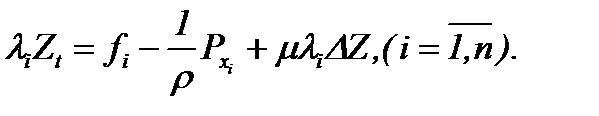 (7.15)
(7.15)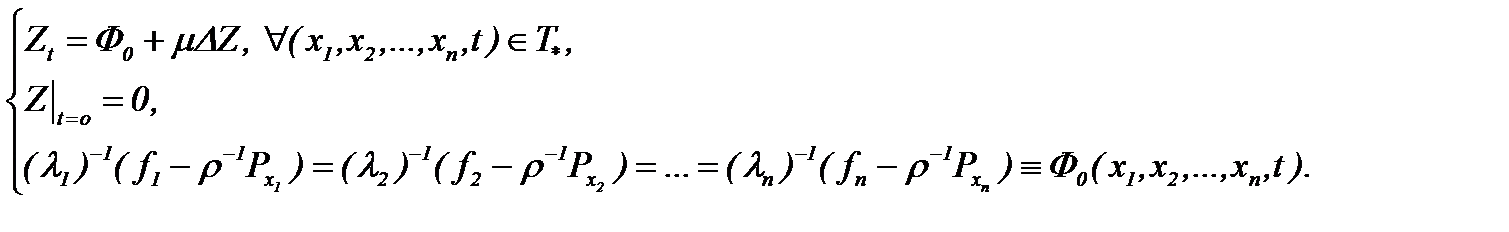 (7.16)
(7.16)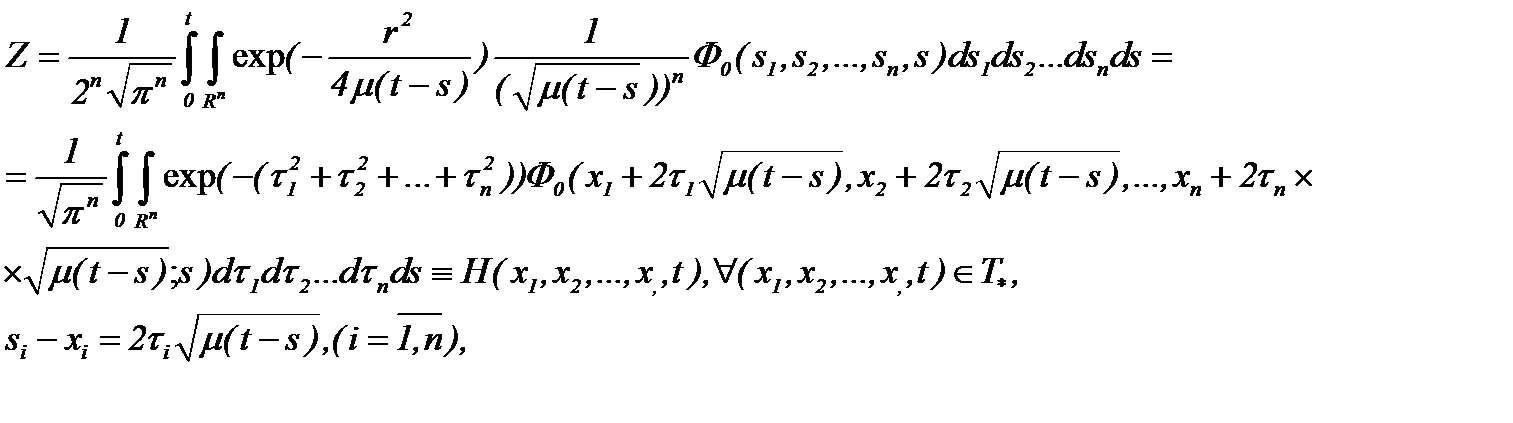 (7.17)
(7.17)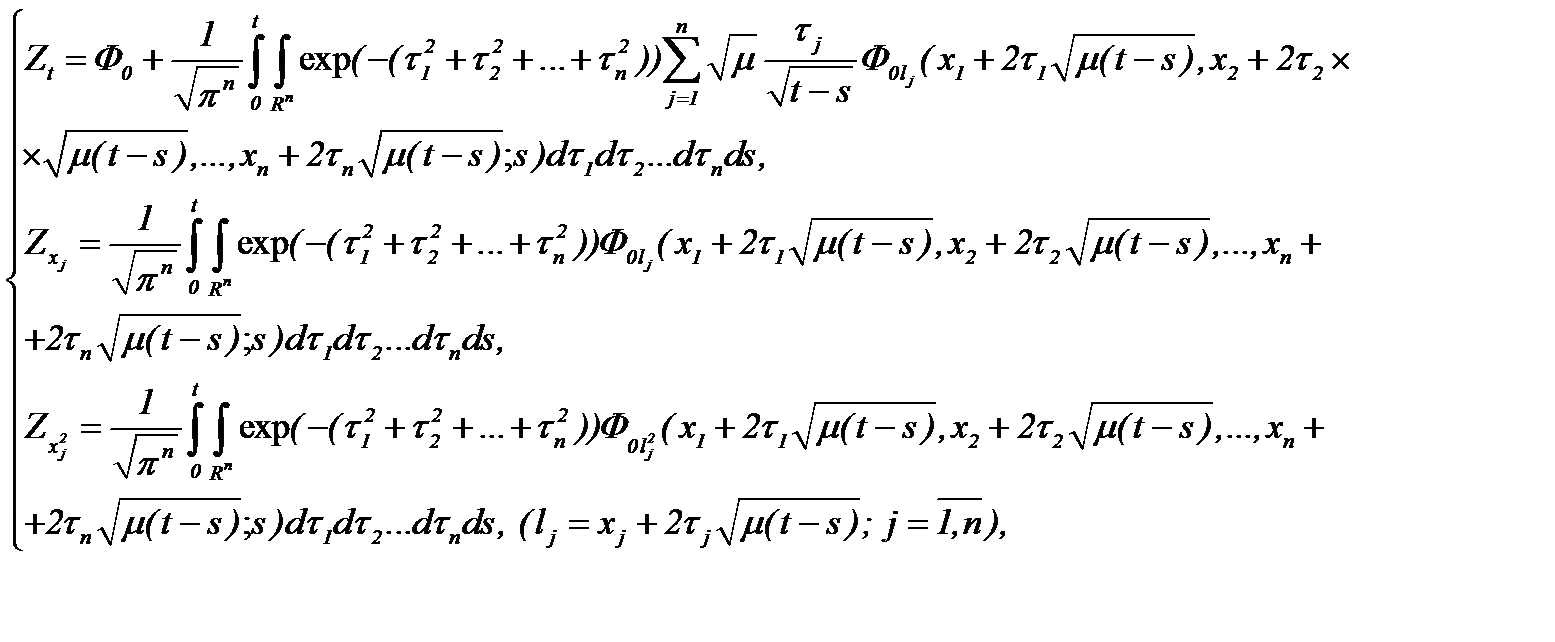 (7.18)
(7.18) 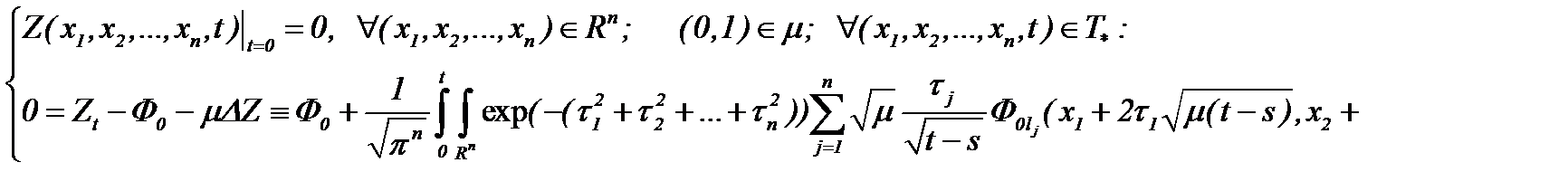
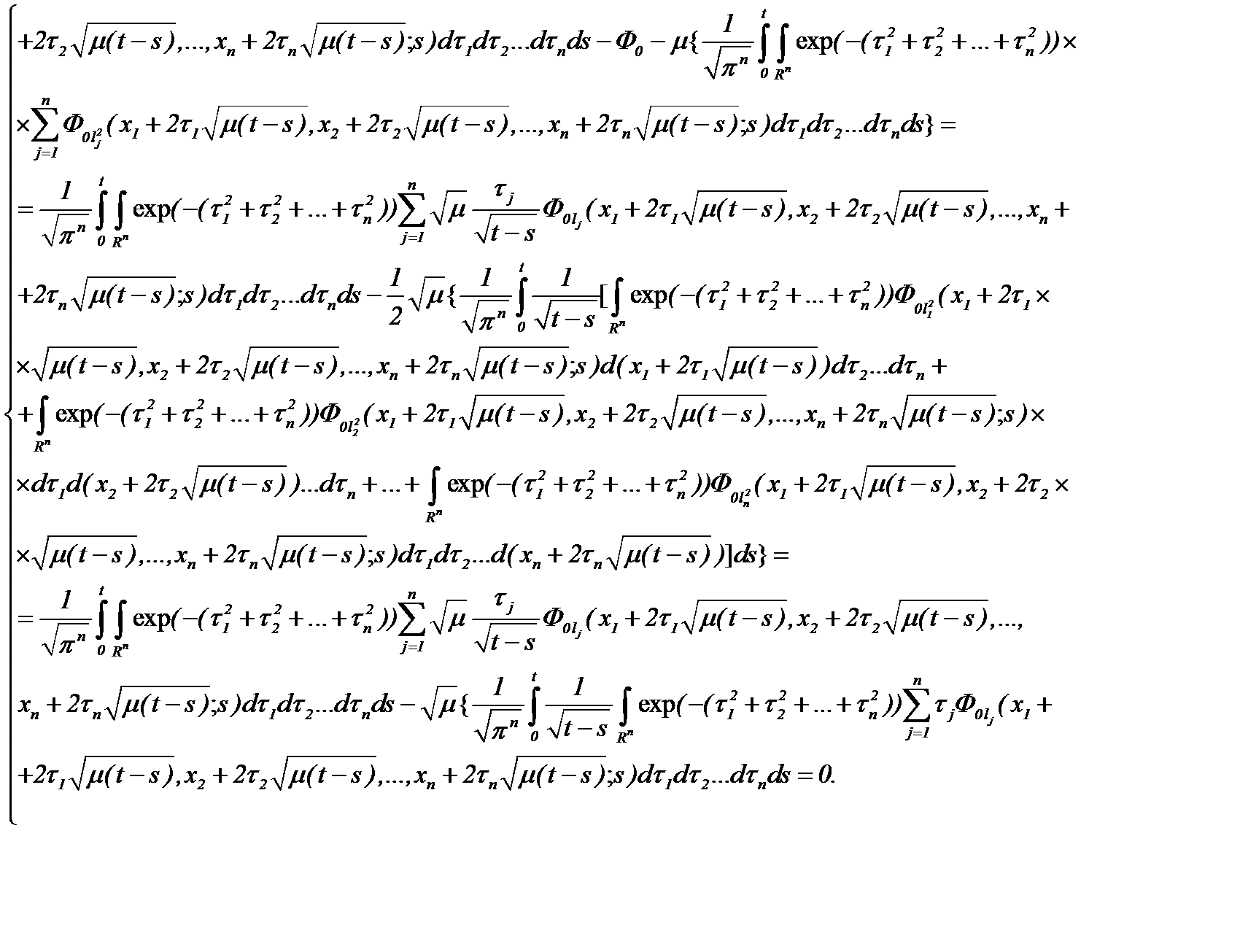
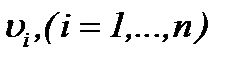 определяются на основе (7.14), а именно
определяются на основе (7.14), а именно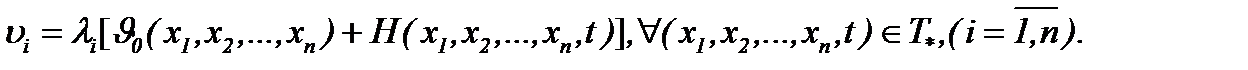 (7.19)
(7.19)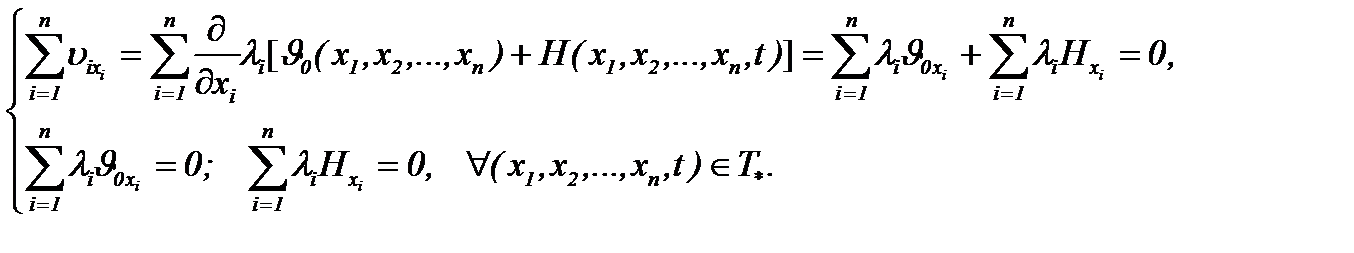
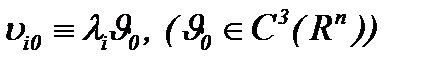 , то решение задачи (1.1)n – (1.3)n ограничено в
, то решение задачи (1.1)n – (1.3)n ограничено в 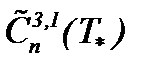 :
: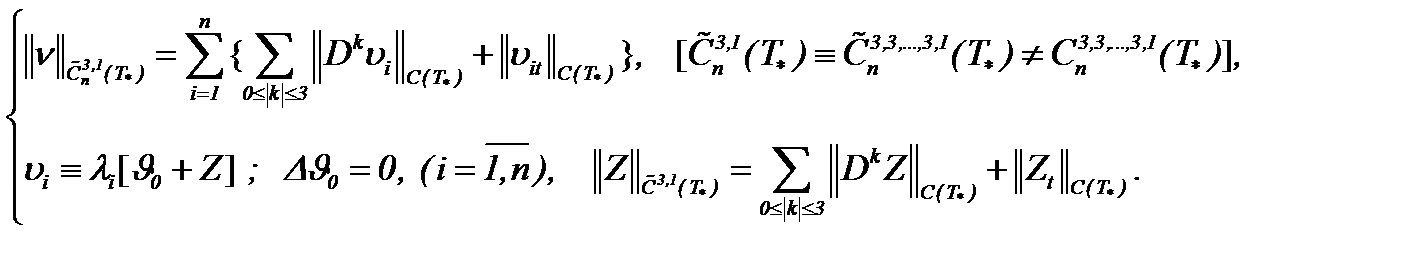
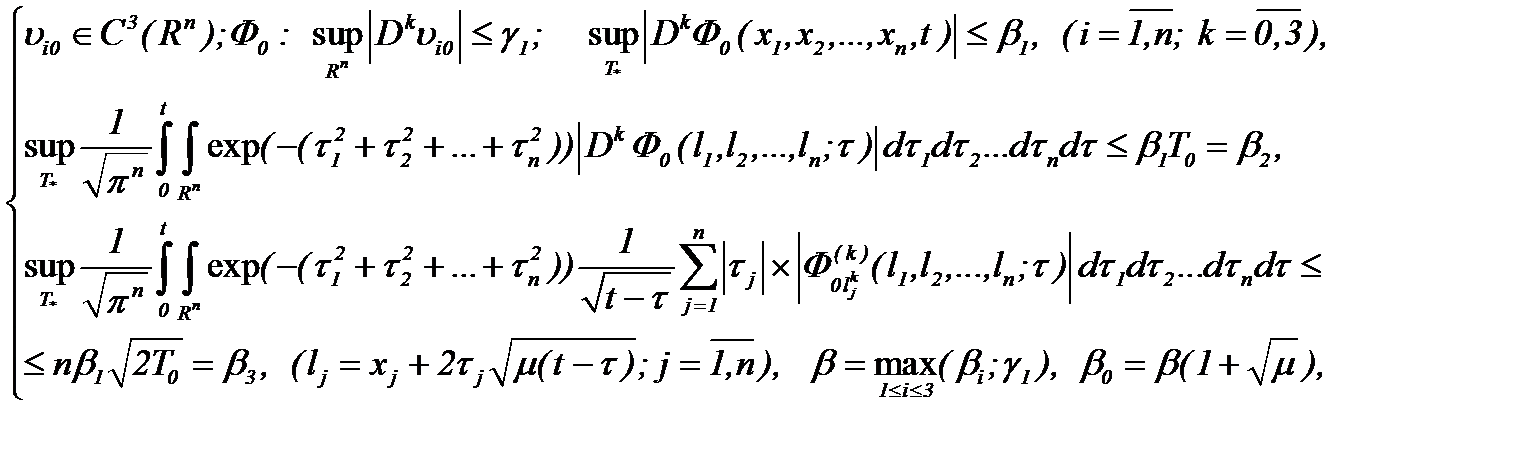 (7.20)
(7.20)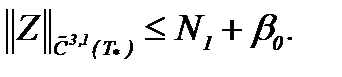
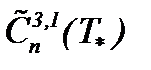 , имеем
, имеем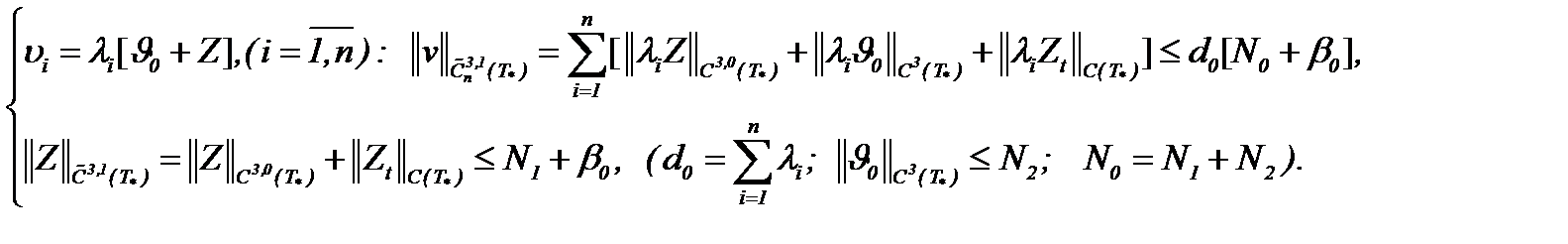
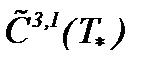 .
.


