

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Построение азимутальной проекции Ламберта подчинено условию равновеликости: по всей ее площади должно быть сохранено условие
 р = а · b = const = 1.
р = а · b = const = 1.
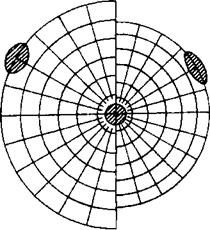
Способ достижения этого условия можно понять из сравнения нормальных картографических сеток, построенных в проекциях Постеля и Ламберта Вспомним, что благодаря равенству отрезков меридианов между параллелями в проекции Постеля и сохранению на меридианах главного масштаба показатель искажения длин по этим главным направлениям равен 1. По второму же главному направлению показатель а больше 1, что влечет увеличение показателя искажения площади к периферии карты.
Чтобы избежать этого и чтобы показатель р = а · b оставался всюду равным единице, в каждой точке карты увеличение одного сомножителя (а) компенсировалось уменьшением второго сомножителя (b). Но это возможно лишь при условии, что отрезки меридианов между параллелями у нормальной сетки не остаются равными (как в проекции Постеля), а уменьшаются кпериферии. Это и осуществлено при построении проекции Ламберта. В результате оказалось выполненным условие равновеликости.
Кроме того, проекция Ламберта имеет следующие свойства:
применительно к трем вариантам картографической сетки: нормальному, поперечному и косому
Во всех трех вариантах точка нулевых искажений находится в центре картографической сетки. Показатели искажения длин по направлениям радиусов от этой точки изменяются от 1 до 0,7 на краю карты полушария. По направлениям, перпендикулярным радиусам, показатель искажения длин а изменяется от 1 в центре до 1,4 на краю карты полушария. Углы и формы претерпевают в этой проекции значительные искажения, особенно к периферии карты. Например, показатель искажения форм на краю карты полушария равен 2,0.
|
|
Проекция Ламберта, предложенная автором в XVIII в., имеет в настоящее время широкое применение. Почти все карты восточного и западного полушарий, в том числе стенные и настольные, в школьных атласах и учебниках строят в азимутальной поперечной проекции Ламберта. В этой же проекции строят карты материков: для Африки применяют поперечную картографическую сетку в проекции Ламберта, для других материков используют косую картографическую сетку.
КОНИЧЕСКИЕ ПРОЕКЦИИ
Коническая нормальная равнопромежуточная проекция Птолемея. Строится на нормальном касательном конусе. Условием построения картографической сетки является сохранение величины главного масштаба по всем меридианам. Сетка может быть создана простым геометрическим построением (хотя она относится к неперспективным)
 Рассмотрим здесь аналитический расчет элементов сетки с помощью рисунка.
Рассмотрим здесь аналитический расчет элементов сетки с помощью рисунка.
Все параллели у этой сетки — дуги концентрических окружностей с центром в точке S (вершине конуса). Формулу радиуса параллели касания конуса (с широтой φ 0) выводят из прямоугольного треугольника АOS, в котором ρ и R — катеты, а угол ASO равен φ0, как образованный взаимно перпендикулярными сторонами
ρ = R –ctg φ0.
Величину промежутков между параллелями узнают по формуле:
2pR ·Dj 0
а = 360°
Обе вычисленные величины (ρ и а) при построении сетки уменьшают в соответствии с выбранным главным масштабом. Как у каждой нормальной конической проекции, меридианы здесь имеют форму прямых линий, сходящихся в точке S под равными углами γ. Угол γ или сближение меридианов пропорционален разности долгот соседних меридианов и широте параллели касания конуса γ = D λ-sin j 0.
Построение сетки объясняет ее свойства: главный масштаб сохраняется по всем меридианам и по параллели касания конуса; частные масштабы по другим параллелям больше главного; показатели n, р и k численно равны между собой. Проекция произвольная, равнопромежуточная.
|
|
Она была впервые применена (или изобретена?) древнегреческим ученым К. Птолемеем во II в н.э. Искажения в ней невелики в полосе карты, ограниченной параллелями, отстоящими на 15° к северу и югу от параллели касания конуса. Поэтому она пригодна для стран, вытянутых с запада на восток. Простота построения сетки позволяет рекомендовать ее для создания рукописных карт участков территории республики, областей и других. За параллель касания конуса выбирают при этом параллель, проходящую через геометрический центр изображаемой территории.
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!