Побудова обчислювальної моделі може здійснюватися різними методами, які можна поділити на точні й наближені. Точні методи - це такі, які після скінченої кількості дій (обчислень) приводять до точного результату за умови, що обчислення здійснюються без похибок. Наближеними називають такі методи, які за тих же умов дозволяють одержати результат лише з деякою похибкою.
При використанні точних методів етап досліджування математичної моделі поділяється на такі підетапи:
1) пошук точного розв'язку математичної моделі;
2) підставляння вихідних даних у знайдений точний розв'язок і реалізація передбачених ним обчислень.
Наприклад, для розв'язування задачі 1 краще використати точний метод, тобто формулу
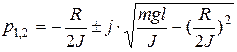 (1.8)
(1.8)
(припускається, що 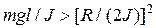 ), але можна застосовувати й наближені способи пошуку коренів квадратного рівняння.
), але можна застосовувати й наближені способи пошуку коренів квадратного рівняння.
Диференційне рівняння (5) задачі 2 краще розв'язувати, розділяючи змінні, тобто приводячи його до вигляду
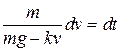 . (1.9)
. (1.9)
Однак, його можна розглядати і як лінійне диференційне рівняння зі сталими коефіцієнтами, або розв'язувати (інтегрувати) наближеними чисельними методами.
При розв'язуванні задачі 3 слід використовувати методи наближеного обчислення визначених інтегралів.
Задачу 4 також можна розв'язувати двома шляхами. Розглядаючи систему диференційних рівнянь (6) як вихідну математичну модель, можна, з одного боку, знайти точний її розв'язок (7), а потім здійснити підставляння значень вихідних даних і досягти явних залежностей 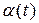 і
і 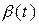 , а отже, й
, а отже, й 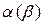 . З іншого боку, до системи (6) можна безпосередньо застосувати методи чисельного інтегрування диференційних рівнянь (наближені методи).
. З іншого боку, до системи (6) можна безпосередньо застосувати методи чисельного інтегрування диференційних рівнянь (наближені методи).
Дослідження математичної моделі наближеними методами поділяється на такі етапи:
1) обрання обчислювального методу (зазвичай наближених чисельних методів буває декілька);
2) вивчення або складання алгоритму метода;
3) реалізація алгоритму за допомогою обчислювальних засобів.
При виборі чисельного методу суттєвими є обсяг обчислень, швидкість збіжності обчислень (як швидко здобувається результат) та інші чинники. Зокрема, обрання методу залежить і від вхідних даних.
Крім того, на вибір метода впливають засоби його реалізації (ручний розрахунок, наявність обчислювальної машини, наявність готової програми тощо). Так, якщо буде використані швидкодіюча ЕОМ і готова програма, то обсяг обчислень не повинен засмучувати виконавця і бути визначальним фактором при обранні метода. При ручному ж розрахункові слід віддати перевагу методу, який, можливо, потребує деяких певних попередніх досліджень і перетворень математичної моделі, але завдяки цьому потребує й значно меншу кількість обчислень.
Алгоритм методу
Алгоритмом метода називається система правил, яка задає точно визначену послідовність операцій, яка приводить до шуканого результату (точного або наближеного).
Алгоритм - одне із ґрунтовних понять математики. Хід розв'язування обчислювальної (і взагалі будь-якої) задачі має бути поданий через алгоритм.
Алгоритм можна записати словесно-формульно або у вигляді схеми. Так, словесно-формульний опис алгоритму розв'язування задачі 1 за формулою (8) має наступний вигляд:
1. Обчислити 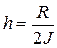 .
.
2. Обчислити 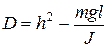 .
.
3. Якщо 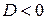 , перейти до п. 7.
, перейти до п. 7.
4. Обчислити 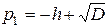 і
і 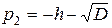 .
.
5. Подати на пристрій виведення інформацію: "Рівняння має два дійсні корені:" і роздрукувати значення шуканих коренів 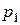 і
і 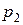 .
.
6. Перейти до п. 8.
7. Вивести на пристрій виведення інформацію:
"Коефіцієнт загасання дорівнює " і вивести значення 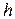
"Частота власних коливань дорівнює" і роздрукувати значення 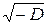 .
.
8. Кінець обчислень.
При виконанні алгоритму перехід від однієї дії до іншої здійснюється строго у порядку їхнього запису. Якщо ж потрібно перервати природний хід дій за деякої умови, слід указувати на це (див. п. 3 наведеного алгоритму).
Структурною схемою алгоритму називають графічне зображення послідовності дій обчислювального процесу.
У схемі кожна дія розміщується у певному геометричному символі (фігурі). Послідовність дій вказується на схемі напрямком стрілок на лініях, якими з'єднують ці символи. Зазвичай прийнято початок і кінець обчислень зображувати овалами, введення даних і виведення результатів - у вигляді паралелограма. Обчислювальні операції розміщуються у прямокутниках, а операція перевірки деякої умови зображується у вигляді ромбу. Усередині кожної фігури розміщується стислий формульний опис відповідної операції. Символи операцій перевірки умови мають два виходи: "так" і "ні". Стрілка на лінії, що виходить із виходу "так" вказує на операцію, до виконання якої потрібно перейти, якщо умову, яка перевіряється, виконано. Стрілка з написом "ні" вказує на операцію, до виконання якої слід перейти у випадку, коли умову не виконано. На рис. 1.2. подані зображуючи елементи блок-схеми алгоритму обчислень. Фігури з'єднуються лініями зі стрілками, які вказують на операцію, до виконання якої слід перейти. Для прикладу на рис 1.3 зображено схему алгоритму пошуку коренів квадратного рівняння.
|
| | 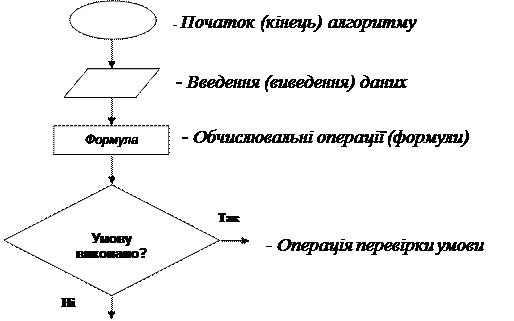 |
Рис. 1.2. Елементи блок-схеми алгоритму
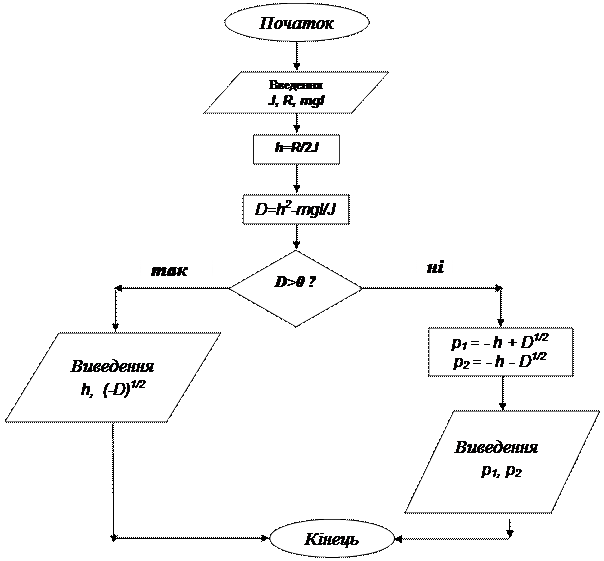
Рис. 1.3. Схема алгоритму відшукання коренів квадратного рівняння
Реалізація методу обчислень
Обчислення за алгоритмами відбувається за допомогою різних обчислювальних засобів. При ручних (безпосередніх) розрахунках зазвичай використовуються найпростіші обчислювальні засоби: логарифмічна лінійка, таблиці, механічні, електричні, електронні клавішні обчислювальні машини. Проміжні результати дій алгоритму треба записувати у спеціальний розрахунковий бланк. Наявність програмувальних мікрокалькуляторів дозволяє реалізовувати обчислення автоматично, під керуванням програми.
Суттєвим є контроль обчислень, який проводять за так званим контрольним прикладом (тестом). Результат контрольного прикладу має бути заздалегідь відомим, тобто він або є очевидним, або його відшукують яким-небудь іншим способом. При ручному розрахунку контроль рекомендується проводити поетапно. При розрахунках на ЕОМ за складеною програмою контрольний приклад заздалегідь прораховують вручну, а потім звіряють поетапно результати розрахунків із здійснюваними машиною.
Контрольні запитання
1. Що таке "модель"?, "моделювання"?
2. Які об'єктивні й суб'єктивні чинники можуть впливати на створювану модель?
3. Які види моделей трапляються в інженерній практиці?
4. Що таке "математична модель", "обчислювальна модель"?
5. Як можна охарактеризувати постановку інженерної задачі?
6. Які етапи проходить у загальному випадку розв'язування інженерної задачі?
7. Що таке "алгоритм"? На які види поділяються алгоритми?
8. Що таке "блок-схема алгоритму"? Які позначення прийняті при побудові блок-схеми алгоритму?
9. Які є загальні правила побудови блок-схеми алгоритму?
Заняття 2. Організація обчислень
Як вже зазначалось, неминучим етапом розв'язування інженерних задач є проведення розрахунків із наближеними вихідними даними. Тому до основних умінь, необхідних інженеру в його професійної діяльності, слід віднести вміння грамотно (раціонально) організувати обчислення, під чим мається на увазі:
n знати можливі джерела похибок;
n уміння правильно записувати наближені дані й результати (у тому числі проміжні);
n уміння оцінювати похибку результату за заданими похибками компонент;
n уміння обирати найбільш раціональний порядок обчислень;
n уміння обирати алгоритм обчислення, найстійкішій до похибок обчислень;
n уміння контролювати хід і результати обчислень із метою виключення грубих похибок.
Не маючи достатніх умінь і навичок практичних обчислень можна при розв'язуванні задачі одержати результат, який не матиме нічого спільного з дійсним розв'язком задачі.
Джерела й види похибок
Практично на кожному етапі розв'язування прикладної задачі виникають свої джерела похибок.
Математична модель - це вже наближене подання реального об'єкта. Вихідні дані, що використовуються у розрахунках і виходять з експерименту, можна визначити лише наближено. Навіть точні числа, такі як 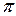 ,
, 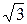 , 6/7 і т.п., при обчисленнях замінюють десятковими дробами, залишаючи лише певну кількість знаків після десяткової коми. Обчислювальні методи у більшості також є наближеними. Навіть при використанні найпростішої формули результат, як правило, одержують наближений.
, 6/7 і т.п., при обчисленнях замінюють десятковими дробами, залишаючи лише певну кількість знаків після десяткової коми. Обчислювальні методи у більшості також є наближеними. Навіть при використанні найпростішої формули результат, як правило, одержують наближений.
Основні джерела виникнення похибок наближеного розв'язування прикладних задач такі.
1. Похибки математичної моделі . Їх пов'язано з використаними припущеннями, які дозволяють спростити математичну модель задачі. Вони не контролюються у процесі чисельного розв'язування задачі і можуть бути зменшені лише за рахунок більш точного математичного опису фізичної задачі.
2. Похибки первісних даних. Значення параметрів, що входять у математичний опис задачі, вимірюються експериментально з деякою похибкою. Похибки математичної моделі і вихідних даних у цілому утворюють так звані неусувні похибки. Назву обумовлено тим, що ці види похибок не можна усунути шляхом організації обчислень. Зменшення їх лежить лише на шляху перебудови математичної моделі і точнішого виміру вихідних даних.
3. Похибки наближеного методу, або похибки усікання. При чисельному розв'язуванні задачі точний оператор, в якому кількість чисел або операцій перевищує допустимі межі, замінюється наближеним, який потребує скінченої кількості операцій. Наприклад, замінюють інтеграл сумою, функцію - поліномом (багаточленом) або будують нескінченний процес і обривають його після скінченої кількості операцій.
4. Обчислювальна похибка, що виникає в результаті вимушеного округлення чисел, наприклад, внаслідок скінченої кількості розрядів у запису числа в оперативній пам'яті ЕОМ.
Якщо розв'язок деякої задачі неперервно залежить від вхідних даних, тобто малому змінюванню вхідних даних відповідає мале змінювання розв'язку, то задача називається стійкою за вхідними даними, або грубою. У стійкому обчислювальному алгоритмі похибки округлення не накопичуються.
Точність наближеного числа характеризується поняттями абсолютної й відносної похибки.
Абсолютною похибкою наближеного числа 'a' називається абсолютне значення різниця між ним і точним його значенням:
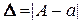 ,
,
де 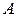 - точне значення,
- точне значення, 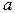 - наближене значення. Абсолютна похибка має суто теоретичний інтерес, оскільки точне значення
- наближене значення. Абсолютна похибка має суто теоретичний інтерес, оскільки точне значення 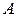 невідоме. Тому на практиці частіше використовують граничну абсолютну похибку
невідоме. Тому на практиці частіше використовують граничну абсолютну похибку 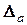 наближеного числа
наближеного числа 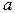 , рівну по можливості найменшому числу, що є більшим за абсолютну похибку
, рівну по можливості найменшому числу, що є більшим за абсолютну похибку
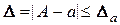 .
.
Значення 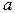 і
і 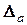 дозволяють вказати інтервал, що містить точне значення
дозволяють вказати інтервал, що містить точне значення 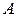 :
:
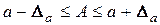 .
.
Частіше використовується компактніший запис
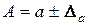 .
.
Очевидно, таке визначення абсолютної похибки не є однозначним. Так, якщо 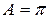 , а як наближене значення взяти
, а як наближене значення взяти 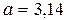 , то, враховуючи, що
, то, враховуючи, що 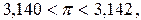 можна записати:
можна записати:
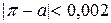 ;
; 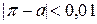 ;
; 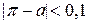 .
.
Кожне з чисел 0,002; 0,01; 0,1 буде граничною абсолютною похибкою числа 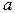 . Але чим ближче між собою числа
. Але чим ближче між собою числа 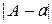 і
і 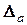 , тим точніше абсолютна похибка оцінює фактичну похибку.
, тим точніше абсолютна похибка оцінює фактичну похибку.
Основною характеристикою точності наближеного числа є його відносна похибка
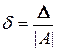 .
.
Оскільки число 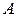 невідоме, то, як правило, вважають
невідоме, то, як правило, вважають
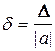 .
.
Аналогічно з нерівності 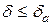 визначають граничну відносну похибку числа
визначають граничну відносну похибку числа 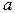 , вважаючи
, вважаючи
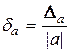 .
.
Величина 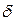 характеризує якість наближення. Це безрозмірна величина, зазвичай її виражають у процентах. Так, відносна похибка числа
характеризує якість наближення. Це безрозмірна величина, зазвичай її виражають у процентах. Так, відносна похибка числа 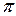 , прийнятого за наближене значення числа
, прийнятого за наближене значення числа 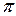 , при
, при 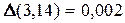 дорівнює
дорівнює
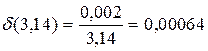 , .
, .





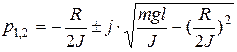 (1.8)
(1.8)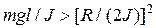 ), але можна застосовувати й наближені способи пошуку коренів квадратного рівняння.
), але можна застосовувати й наближені способи пошуку коренів квадратного рівняння.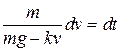 . (1.9)
. (1.9)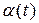 і
і 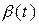 , а отже, й
, а отже, й 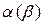 . З іншого боку, до системи (6) можна безпосередньо застосувати методи чисельного інтегрування диференційних рівнянь (наближені методи).
. З іншого боку, до системи (6) можна безпосередньо застосувати методи чисельного інтегрування диференційних рівнянь (наближені методи).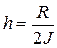 .
.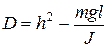 .
.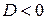 , перейти до п. 7.
, перейти до п. 7.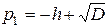 і
і 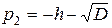 .
.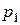 і
і 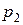 .
.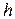
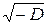 .
.

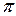 ,
, 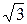 , 6/7 і т.п., при обчисленнях замінюють десятковими дробами, залишаючи лише певну кількість знаків після десяткової коми. Обчислювальні методи у більшості також є наближеними. Навіть при використанні найпростішої формули результат, як правило, одержують наближений.
, 6/7 і т.п., при обчисленнях замінюють десятковими дробами, залишаючи лише певну кількість знаків після десяткової коми. Обчислювальні методи у більшості також є наближеними. Навіть при використанні найпростішої формули результат, як правило, одержують наближений.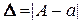 ,
,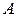 - точне значення,
- точне значення, 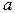 - наближене значення. Абсолютна похибка має суто теоретичний інтерес, оскільки точне значення
- наближене значення. Абсолютна похибка має суто теоретичний інтерес, оскільки точне значення 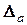 наближеного числа
наближеного числа 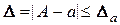 .
.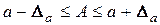 .
.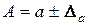 .
.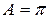 , а як наближене значення взяти
, а як наближене значення взяти 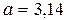 , то, враховуючи, що
, то, враховуючи, що 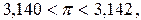 можна записати:
можна записати: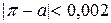 ;
; 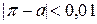 ;
; 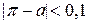 .
.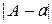 і
і 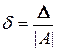 .
.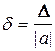 .
.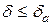 визначають граничну відносну похибку числа
визначають граничну відносну похибку числа 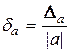 .
.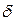 характеризує якість наближення. Це безрозмірна величина, зазвичай її виражають у процентах. Так, відносна похибка числа
характеризує якість наближення. Це безрозмірна величина, зазвичай її виражають у процентах. Так, відносна похибка числа 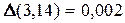 дорівнює
дорівнює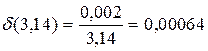 , .
, .


