Ми пам'ятаємо, що мікростан системи великої кількості частинок нестійкий навіть при малих флуктуаціях. Це означає, що передбачати стан макросистеми неможливо в принципі. Мікроподії в макросистемі є істинно випадковими. Головне завдання статистичної фізики - знаходити вірогідність станів і мікроподій.
На минулому занятті ми розглянули алгоритм, що дозволяє змоделювати випадкові блукання (одновимірний випадок) ансамблю з М частинок (незалежних один від одного), і оцінити, як виконується параболічний закон дифузії (середній квадрат зсуву частинки пропорційний часу випадкових блукань). У цьому завданні ми обчислюємо середній квадрат зсуву, усереднений по ансамблю.
Сьогодні ми розглянемо подібний алгоритм, (і подібну модель), але поставимо завдання одержати на виході програми розподіл вірогідності положення частинок при випадкових одновимірних блуканнях.
Постановка завдання: нехай частинка може рухатися вправо з вірогідністю р, а вліво з вірогідністю q=1-p з однаковим кроком h. Необхідно визначити, з якою вірогідністю PN(x) через N кроків частинка знаходитиметься на відстані N від початкової точки x0=0.
Очевидно, що тут можна було б використовувати комп'ютер як генератор всіх можливих перестановок блукань. Наприклад, якщо розглянути 3 кроки випадкових блукань, то 8 можливих траєкторій виглядають таким чином:
® ® ; ® ®; ® ®;
®; ® ; ® ;
Тобто в нас можливі два варіанти із зсувом на 3 кроки (вправо з вірогідністю р3 або вліво з вірогідністю q3) і 6 варіантів зсуву на 1 крок (3 вправо з вірогідністю p2q або три вліво з вірогідністю pq2). Тоді середній зсув:
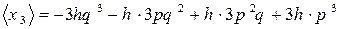
Кількість можливих траєкторій блукань в одновимірному випадку 2N (для нашого випадку - 8), тоді для d-мірного простору підрахунок кількості блукань обмежений через громіздкість операцій.
Альтернативним варіантом може бути вибірка, статистичний характер якої дасть нам інформацію про процес в цілому. Якщо розглянути ансамбль частинок, кожна з яких незалежно від інших проходить випадковий шлях довжиної N кроків з початкової точки, то більшість частинок після однакової кількості кроків матимуть однакову координату XN. Тобто, для визначення вірогідності знаходження частинки в точці X моделюється багато її запусків (М), за якими проводиться усереднювання для визначення середнього зсуву на N кроків і визначається вірогідність появи частинки в заданій точці X як:
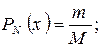 де m- число запусків із зсувом X.
де m- число запусків із зсувом X.
В результаті ми одержали (графічно) розподіл вірогідності у вигляді:
Статистичний характер завдання полягає в тому, що ми розглядаємо або велику кількість випадкових блукань, або велику кількість однакових частинок, які рухаються одночасно.
Завдання: показати, що, продовживши ці розподіли, можна одержати другий закон Фіка (1855) - рівняння дифузії 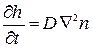 - що говорить про те, що випадкові блукання частинок приводять до перерозподілу їх концентрації згідно вказаному закону.
- що говорить про те, що випадкові блукання частинок приводять до перерозподілу їх концентрації згідно вказаному закону.
Запишемо алгоритм побудови графіка розподілу вірогідності при випадкових одновимірних блуканнях - гістограми PK(m) з шириною стовпця 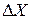 . М - число частинок, положення яких після N кроків відповідає умові:
. М - число частинок, положення яких після N кроків відповідає умові:
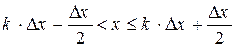

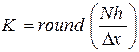 ; (Nh - максимально можливий зсув)
; (Nh - максимально можливий зсув)
Алгоритм 2
Тестовий приклад: М=1000, N=100, h=2, X=5.
Примітка 1: початок координат 320, 440, масштабний множник 2.
Координати додаткових вузлів стовпця:
(320+k2 xx 440);
(320+k2x+x 440+2pk])
Завдання: Перевірити, що одержаний розподіл - є розподілом Гауса. Використовувати метод найменших квадратів для значень ((kx)2, ln(pk])) для нульових значень масиву P, оскільки для розподілу Гауса:
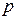 ~
~ 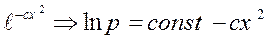 .
.
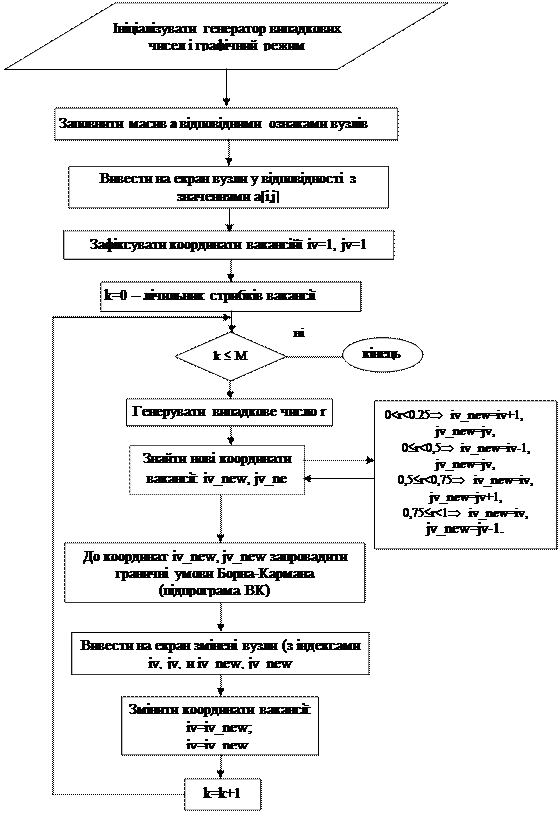
Щоб завершити нашу "екскурсію в область дифузії", розглянемо алгоритм моделі, яка реалізовує вакансійний механізм дифузії між атомами різного сорту методом МК.
Ми використовуватимемо модель плоских квадратних граток, кожному вузлу яких відповідає елемент масиву а. Осередки масиву (вузли) мають ознаки, по яким визначається сорт атома і вакансій (наприклад, цілі числа, які можна використовувати, як колір виведення осередків на екран). Спочатку приймемо, що права половина гратки зайнята атомами сорту А. (зелені, значення 2), ліва - атомами сорту В (блакитні - 3). Вакансію розмістимо в одному вузлі гратки, для визначеності виберемо верхній лівий кут (значення елементу масиву - 8). Нескінченність гратки nn забезпечимо граничними умовами Борна-Кармана, на кожному кроці методом МК випадково вибираємо напрям стрибка вакансії завдовжки h в одному з чотирьох можливих напрямів і міняємо місцями вакансію і вибраний атом. Задамося числом стрибків М.
| Поменять местами вакансию и атом с координатами iv_new, jv_new
a[iv, jv]=a[iv_new, jv_new]
a[iv_new, jv_new]=8
| |
Тестовий приклад: n=30; M=104.
Алгоритм 3






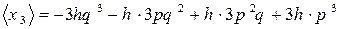
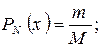 де m- число запусків із зсувом X.
де m- число запусків із зсувом X.
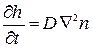 - що говорить про те, що випадкові блукання частинок приводять до перерозподілу їх концентрації згідно вказаному закону.
- що говорить про те, що випадкові блукання частинок приводять до перерозподілу їх концентрації згідно вказаному закону.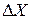 . М - число частинок, положення яких після N кроків відповідає умові:
. М - число частинок, положення яких після N кроків відповідає умові: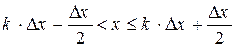

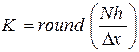 ; (Nh - максимально можливий зсув)
; (Nh - максимально можливий зсув)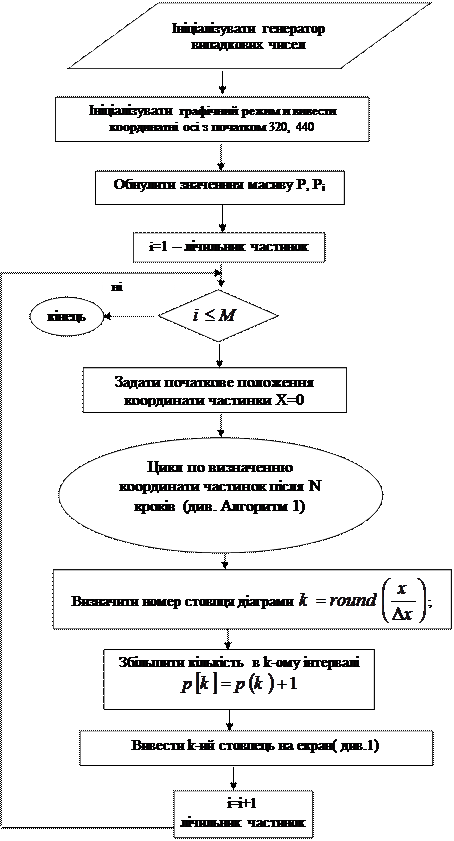
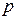 ~
~ 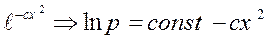 .
.