Перед цим ми розглянули приклади розрахунків похибок результатів обчислень, обумовлених впливом похибок вихідних даних. Тепер же зосередимо увагу на похибках результату обчислень за рахунок похибок округлення.
При виконанні арифметичних дій на будь-якому обчислювальному пристрої (логарифмічній лінійці, калькуляторі або ЕОМ) неминуче округлення проміжних результатів до певної кількості розрядів, а арифметичні операції з округленням мають інші властивості, аніж точні операції. Так, точні операції є комутативними, асоціативними і дистрибутивними. Ті ж операції, реалізовані на обчислювальному пристрої (ОП), вже не є такими.
Машинна арифметика має власні характерні особливості. Правильно враховуючи їх, можна досягти високої ефективності у розв'язуванні задач на ЕОМ. Неуважність до цих особливостей нерідко приводить до помилкових результатів.
Нехай обчислення відбуваються на ЕОМ, в якій кожне число подається п'ятьма значущими цифрами. Складемо два числа
9,2654+7,1625 = 16,4279.
Результат містить 6 значущих цифр і не вміщується у розрядну сітку машини. Його буде округлено до 16,428, і при цьому виникне (крім похибки внаслідок похибок вихідних даних) похибка округлення.
Оскільки ОП працює завжди з фіксованою кількістю розрядів, то округлення виникає весь час при запису проміжних результатів у пам‘ять машини. Округлення полягає у корегуванні останнього (молодшого) розряду. Але й буває, що ніякого корегування не відбувається, а відкидається частина числа, яка не вміщується. Похибка округлення при цьому більша, але значне скорочення машинного часу й довжини робочої програми у цілому є економічно вигідними.
Число у машині подається у такому нормалізованому вигляді
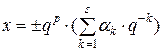 , (2.6)
, (2.6)
де  - основа системи позиційного зчислення;
- основа системи позиційного зчислення; 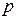 - порядок числа;
- порядок числа;  - кількість значущих розрядів (додатне ціле);
- кількість значущих розрядів (додатне ціле);  - цифри числа у заданій системі зчислення, причому вважається, що
- цифри числа у заданій системі зчислення, причому вважається, що 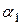 не дорівнює нулеві. Так, для десяткової системи зчислення
не дорівнює нулеві. Так, для десяткової системи зчислення  , порядок числа -
, порядок числа -  , кількість значущих десяткових розрядів -
, кількість значущих десяткових розрядів -  , цифри
, цифри 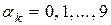 . Наприклад, для числа
. Наприклад, для числа  десятковий порядок дорівнює
десятковий порядок дорівнює  , кількість значущих розрядів
, кількість значущих розрядів  , а цифри
, а цифри

 .
.
У нормалізованій формі (6) вираз у дужках подає так звану мантису числа. Мантиса у нормалізованому десятковому поданні завжди менша за одиницю і більша або дорівнює 0,1. У цілому будь-яке число однозначно описується трьома його характеристиками:
1) знаком числа;
2) значенням мантиси (вираз у дужках у (6));
3) цілим числом  - порядком числа.
- порядком числа.
ЕОМ працюють в основному у двійковій системі зчислення, тому для них  . Обсяг оперативній пам'яті ЕОМ, який віддається на запис поодинокого окремого числа, вимірюється у байтах (8 двійкових розряди - бітів) і залежить від мови програмування, на який записано програму, і типу числа, під яким його оголошено у програмі.
. Обсяг оперативній пам'яті ЕОМ, який віддається на запис поодинокого окремого числа, вимірюється у байтах (8 двійкових розряди - бітів) і залежить від мови програмування, на який записано програму, і типу числа, під яким його оголошено у програмі.
Наприклад, у мові Fortran під запис цілого числа типу INTEGER відводять 2 байти, тобто 16 двійкових розряди. Один із цих розрядів займає запис знака числа (додатне число чи від'ємне). У решті розрядів записується абсолютне значення цього числа. Неважко зрозуміти, що у такий обсяг можна записати число, за абсолютним значенням не більше за 32512.
Довільне число типу REAL записується у Фортрані у 4 байти оперативної пам'яті. З 32 бітів цього обсягу один біт займає запис знака числа, 7 розрядів - двійковий запис десяткового порядку числа (із них 1 розряд - запис знака порядку) і 24 розряди займає запис мантиси числа. З цього випливає, що абсолютне значення порядку десяткового числа у цьому випадку не перевищує 32. Тобто тип REAL дозволяє оперувати з числами за абсолютним значенням від  до
до  . При цьому мантиса числа, маючи для запису 24 розряди, зберігає
. При цьому мантиса числа, маючи для запису 24 розряди, зберігає  десяткових розрядів числа. Тобто розглядуваний тип зберігає сім вірних десяткових цифр у кожному числі.
десяткових розрядів числа. Тобто розглядуваний тип зберігає сім вірних десяткових цифр у кожному числі.
Розглянемо типи даних, передбачені мовою Паскаль.
Тут для подання цілих чисел існують 5 типів даних:
n byte - займає 1 байт пам'яті; за його допомогою можуть зберігатися цілі додатні числа від 0 до 255;
n shortint (коротке ціле) - займає теж 1 байт пам'яті; цей тип зберігає цілі числа від -128 до 127;
n integer (ціле) - для даних цього типу відводять 2 байти пам'яті; за його допомогою записуються цілі числа від -32768 до +32767;
n word - займає теж 2 байти; ним записуються лише додатні цілі від 0 до 65535;
n longint (довге ціле) - обіймає 4 байти пам'яті; зберігає числа від - 2.147.483.648 до + 2.147.483. 647.
Дійсні дані у Паскалі подані наступними типами:
n single - на запис числа цього типу відводять 4 байти пам'яті, з них 24 біти займає запис мантиси, а 7 бітів - запис порядку числа; ним можуть бути подані дійсні числа з абсолютним значенням від  до
до  і з 7 вірними десятковими розрядами;
і з 7 вірними десятковими розрядами;
n real - займає 6 байтів (48 бітів); із них 7 бітів - запис порядку, а 40 бітів - мантиса числа; записуються числа з абсолютним значенням від  до
до  з 12 вірними десятковими розрядами;
з 12 вірними десятковими розрядами;
n double - запис має обсяг у 8 байтів (64 бітів), запис порядку займає 10 бітів, запис мантиси - 54 бітів; ним зберігаються числа з абсолютним значенням від  до
до  і з 16 вірними десятковими розрядами;
і з 16 вірними десятковими розрядами;
n extended - тип, під який відводять 10 байтів оперативної пам'яті (14 бітів - під запис порядку і 65 - під запис мантиси); при цьому забезпечується збереження чисел від 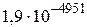 до
до  з 19 вірними десятковими розрядами.
з 19 вірними десятковими розрядами.
У середовищі комп'ютерної системи MatLAB усі числові дані мають тип double, який по всіх показниках збігається з відповідним типом мови Паскаль.
Максимальна відносна похибка округлення при записі числа у пам'ять ЕОМ залежить не від його величини, а лише від кількості 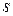 десяткових розрядів у запису мантиси у його поданні на ЕОМ:
десяткових розрядів у запису мантиси у його поданні на ЕОМ:
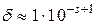 .
.
Наприклад, для типу REAL у Фортрані  , для того ж типу мови Паскаль
, для того ж типу мови Паскаль 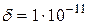 . Дані типу double у мові Паскаль і системі MatLAB мають елементарну похибку округлення
. Дані типу double у мові Паскаль і системі MatLAB мають елементарну похибку округлення
 . (2.7)
. (2.7)
Розглянемо процес поширення похибок округлення при обчисленнях і впливу їх на похибку визначення результату обчислення.
Припустимо, потрібно скласти на ЕОМ дві величини
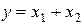 .
.
Цей процес розкладається на 4 етапи:
1) запис числа  у пам'ять ЕОМ; при цьому, навіть коли вихідне значення
у пам'ять ЕОМ; при цьому, навіть коли вихідне значення  відоме точно, при його записі може виникнути похибка округлення
відоме точно, при його записі може виникнути похибка округлення 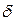 (це може бути, якщо точне значення величини містить більшу кількість десяткових розрядів, ніж
(це може бути, якщо точне значення величини містить більшу кількість десяткових розрядів, ніж  - кількість розрядів для запису числа в ЕОМ):
- кількість розрядів для запису числа в ЕОМ): 
 ;
;
2) запис числа 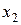 у пам'ять; це приводить до появи аналогічної похибки
у пам'ять; це приводить до появи аналогічної похибки 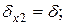
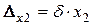 ;
;
3) підсумовування величин  і
і 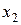 ; при цьому перші дві похибки вплинуть на результат сумування
; при цьому перші дві похибки вплинуть на результат сумування 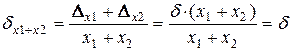 ;
;
4) запис результату у пам'ять; при цьому може виникнути похибка округлення 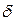 , якуо кількість розрядів в результаті перевищує кількість розрядів у запису числа у пам'ять; у цілому результуюча відносна похибка результату може сягати величини
, якуо кількість розрядів в результаті перевищує кількість розрядів у запису числа у пам'ять; у цілому результуюча відносна похибка результату може сягати величини  , а абсолютну похибку сумування можна оцінити за формулою
, а абсолютну похибку сумування можна оцінити за формулою  .
.
Якщо тепер перейти до сумування (послідовного) трьох величин
 ,
,
то, повторюючи попередній аналіз, дістанемо
n похибка результату першого підсумовування  знайдена перед цим
знайдена перед цим  ;
;
n похибка запису числа 
 ;
;
n похибка сумування (проходження похибок вихідних даних) 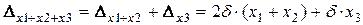 ;
;  ;
;
n похибка запису результату у пам'ять ЕОМ - 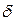 .
.
Разом, одержуємо
 ;
;
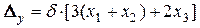 .
.
Поширення цього результату на підсумовування 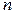 чисел
чисел
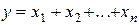
приводить до наступних висновків
 ; (2.8)
; (2.8)
 .
.
Одержаний результат є слушним у випадку, коли усі доданки додатні. Якщо вони усі від'ємні, можна користуватися одержаними результатами, розуміючи в них під 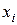 їхні абсолютні значення.
їхні абсолютні значення.
Становище різко змінюється при відніманні чисел (підсумовуванні чисел із протилежними знаками).
Отже, нехай  ;
;  . Повторюючи попередні міркування, одержимо
. Повторюючи попередні міркування, одержимо
 . (2.9)
. (2.9)
Як бачимо, похибка при відніманні чисел більше за похибку при їхньому додаванні у 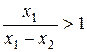 разів. Якщо віднімаються близькі величини, ця похибка може бути вельми значною.
разів. Якщо віднімаються близькі величини, ця похибка може бути вельми значною.
Приклад 1. Нехай  ,
,  . Оцінимо похибку віднімання цих чисел.
. Оцінимо похибку віднімання цих чисел.
Вважаючи, що відносна похибка округлення  , із формули (9) одержимо
, із формули (9) одержимо
 .
.
Ця похибка більша за похибку підсумовування тих самих чисел у 17 500 разів.
Приклад 2. Порівняємо похибки одержання того самого результату за двома формулами
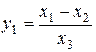 ;
;  .
.
Похибки округлення при розрахунку згідно першої формули:
1) занесення  у пам'ять:
у пам'ять:  ;
;  ;
;
2) занесення 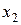 у пам'ять:
у пам'ять:  ;
;  ;
;
3) віднімання  і
і 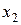 :
:
 ;
; 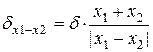 ;
;
4) занесення різниці у пам'ять  ;
;
5) занесення  у пам'ять:
у пам'ять: 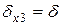 ;
;
6) ділення  ;
;
7) занесення результату у пам'ять 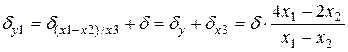 .
.
Оцінка похибок розрахунку за другою формулою:
1) занесення  у пам'ять:
у пам'ять:  ;
;  ;
;
2) занесення  у пам'ять:
у пам'ять: 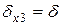 ;
;
3) ділення  на
на  :
:  ;
; 
4) занесення результату у пам'ять 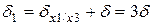 ;
;  ;
;
5) аналогічно похибка від другого ділення 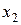 на
на  :
:  ;
;  ;
;
6) віднімання : 

7) занесення результату у пам'ять
 .
.
Тепер можна порівняти похибки розрахунків за цими двома формулами, поділивши похибку за другою формулою на похибку за першою:
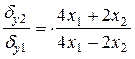 .
.
Якщо, наприклад, 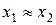 , то розрахунок за другою формулою приведе до похибки у 3 рази більшій, ніж розрахунок за першою формулою.
, то розрахунок за другою формулою приведе до похибки у 3 рази більшій, ніж розрахунок за першою формулою.
Приклад 3. Розглянемо відносну похибку результату обчислень, обумовлену округленням, для двох варіантів обчислення площі тонкого кільця
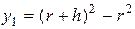 ;
; 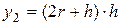 .
.
Нехай 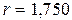 ;
;  . Відносні похибки вихідних даних покладемо рівними нулеві. Елементарну відносну похибку при округленні приймемо рівною
. Відносні похибки вихідних даних покладемо рівними нулеві. Елементарну відносну похибку при округленні приймемо рівною  .
.
РОЗВ'ЯЗУВАННЯ.
Розрахунки похибок за першою формулою:
1) при додаванні Ошибка! Закладка не определена. і запису результату у пам'ять  ;
;
2) при піднесенні у квадрат попередня відносна похибка подвоїться, а при запису результату додасться ще 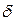 :
:  ;
;  ;
;
3) при записі результату множення 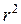 у пам'ять виникає похибка округлення
у пам'ять виникає похибка округлення 
4) при обчисленні різниці абсолютні похибки додаються 
 .
.
Розрахунки похибок за другою формулою:
1) відносна похибка після занесення результату додавання  у пам'ять
у пам'ять  ;
;
2) відносна похибка після множення результату на 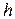 і занесення результату у пам'ять
і занесення результату у пам'ять 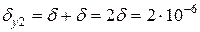 .
.
Відношення одержаних похибок дорівнює
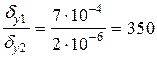 .
.
Отже, похибка результату при обчисленні різниці двох близьких величин у 350 разів більша за похибку за формулою, яка виключає таке віднімання.
Резюмуючи, слід відзначити таку важливу особливість похибок округлення, яка відрізняє її від інших видів похибок: похибки внаслідок округлення проміжних результатів можуть накопичуватися, внаслідок чого підсумкова похибка збільшується із зростанням кількості здійснених операцій. З цього випливає, що основним засобом зменшення підсумкової похибки округлення є зменшення кількості обчислювальних операцій.
ВИСНОВКИ. Задля зменшення похибок результату обчислень внаслідок округлення проміжних результатів слід уживати наступних заходів:
1) потрібно зводити до мінімуму кількість арифметичних дій;
2) додавання чисел слід здійснювати у порядку зростання їхніх абсолютних величин;
3) по можливості потрібно уникати віднімання близьких величин;
4) якщо при обчисленнях зустрічаються різниці близьких величин, слід спочатку обчислити ці різниці, а лише потім здійснити решту операцій.
Контрольні запитання
1. Що вміщує вміння раціонально організувати обчислювальний процес?
2. Які є джерела виникнення похибок при обчисленнях?
3. Що таке "неусувні" похибки? З яких саме похибок складаються вони?
4. Що таке похибки "усікання"? похибки округлення? похибки поширення?
5. Дайте визначення поняттю абсолютної похибки, граничної абсолютної похибки наближеного числа.
6. Що таке відносна похибка? Чим визначається відносна похибка при округленні числа?
7. Перелічіть основні правила, що дозволяють зменшити вплив на похибку результата обчислень похибок вихідних даних.
8. Перелічіть основні правила, що дозволяють зменшити вплив на похибку результата обчислень похибок округлення.
1. Загальне уявлення про фізичне моделювання. Поняття моделі
В науці під моделлю розуміють об'єкт (явище, система, установка, знакове утворення), що має властивість подібності до модельованого об'єкту.
Під подібністю розуміють взаємно-однозначну відповідність між двома об'єктами.
Наприклад, для механічних явищ макросвіту відомі закони механіки Ньютона є математичною моделлю.
Питання. Навіщо потрібне моделювання?
Побудова будь-яких моделей пов'язане з процесом пізнання.
Модель в загальному розумінні є створюваний з метою отримання і (або) зберігання інформації специфічний об'єкт у формі уявного образу, опис знаковими засобами (формули, графіки і ін.), матеріального предмету, що відображає властивості, характеристики і зв'язки об'єкту, істотні для вирішуваної задачі.
Питання. Скільки моделей може існувати для одного об'єкту?
Безліч різних моделей пов'язаних з різними завданнями. Модель завжди бідніша за оригінал. Важливою властивістю моделі є наявність обмежень і допущень, пов'язаних з вирішуваною задачею і властивостями об'єкту, – оригіналу, ресурсами для вирішення завдання.
Етапи побудови моделі.
Основним методом дослідження фізичних об'єктів в даному курсі буде математичне і чисельне моделювання, тобто опис досліджуваної системи або процесів у вигляді різних математичних співвідношень і підрахунок чисельних значень тих характеристик, які нас цікавлять. При побудові моделі в пункті 3 можна виділити 3 основних шляхи подолання затруднень, що виникають при ідеалізації моделі:
1. Розділення складної системи на сукупність простих підсистем.
2. Перехід до іншої ідеалізації (наближенню). Наприклад, від розподілених параметрів до зосереджених.
3. Скорочення числа змінних, використовуючи основні положення теорії подібності і створюючи безрозмірні комплекси. Додамо ще практичні прийоми: зниження розмірності завдань (3-х мірна переходить в 2- х і т. д.)
4. Розробка детермінованих моделей замість стохастичних; заміна змінних константами, ідеалізація властивостей середовища (ідеальний газ, рідина); усереднювання властивостей за об'ємом і напряму; використання лінійних залежності замість нелінійних (лінеаризація).
Класифікація математичних моделей.
Модель, яку належить створити, дуже важливо класифікувати. Це полегшує вибір істотних ознак досліджуваного об'єкту, математичного апарату для його опису, методу побудови моделі. Розглянемо один з варіантів класифікації по Нейману Я. Р. (Моделі в науці і техніці. Л. Наука, 1984), де об'єкти моделювання розглядаються відповідно до їх попарно-протилежним властивостям.
| Неперервні (континуальні) - вхідні і вихідні параметри неперервні. При математичному описі описуються диференціальними, інтегральними, інтегрально-диференціальним рівняннями.
Стаціонарні - по ступені мінливості в часі, постійність основних параметрів в часі.
| Дискретні - можуть приймати кінцеве число відомих значень. При описі використовують: математичну логіку, теорію автоматів – розділ теорії систем, що управляють, що вивчає моделі перетворювачів дискретної інформації.
Нестаціонарні- зміна параметрів в часі.
|
Поняття динаміки пов'язують з умовами протікання процесів, при яких виявляються інерційні ефекти, що визначаються швидкістю зміни запасів енергії і речовини, що акумулюються об'єктом в часі. У динамічних системах стан системи в даний момент пов'язаний з діями, що діють на неї і в даний момент, і в попередні моменти (їх наслідки).
Пов'язані з наслідком динамічні ефекти властиві і механічній формі руху, і процесам дифузії, теплопереносу.
Формально наслідок відбивається шляхом завдання краєвих умов у відповідних диференціальних рівняннях.
|
За характером просторової структури
|
| Моделі із зосередженими параметрами. Використовуються середні значення вхідних характеристик об'єкту, локалізованих в окремих вузлах підсистем.
Моделі описуються диференціальними, трансцендентними або звичайними рівняннями алгебри.
| Моделі з розподіленими параметрами.
Вхідні і вихідні характеристики залежать від координат. У математичній моделі обов'язково присутні просторові координати (диференціальні рівняння в частинних похідних).
|
|
За розмірністю
|
| Одновимірні, з одним вхідним параметром.
| Багатовимірні - мають N вхідних параметрів.
Якщо система має ще і декілька вихідних параметрів, то в загальному випадку кожен вихід залежить від декількох змінних, багатовимірна модель ще і багатозв'язкова.
|
|
За ступенем лінійності об'єкту
|
| Лінійні об'єкти
Серед коефіцієнтів, що входять в його математичний опис, відсутні величини, залежні від вхідних змінних, їх похідних і інтегралів.
| Нелінійні об'єкти - наявність залежних коефіцієнтів.
|
Можна сказати, що життя принципово нелінійне, проте при створенні математичних моделей часто вдається ввести наближення, при яких вдається з високою точністю описувати систему за допомогою лінійних рівнянь.
|
За математичними методами рішення поставленої задачі
|
| Аналітичні моделі
Об'єкт описаний на підставі відомих фізичних законів, дослідження ведеться математичними методами, що дозволяють одержати аналітичне рішення поставленої задачі.
| Чисельні математичні моделі
Для отримання рішень використовують чисельні методи, якщо завдання важко піддається або зовсім не піддається аналітичному рішенню.
|



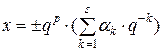 , (2.6)
, (2.6) - основа системи позиційного зчислення;
- основа системи позиційного зчислення; 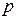 - порядок числа;
- порядок числа;  - кількість значущих розрядів (додатне ціле);
- кількість значущих розрядів (додатне ціле);  - цифри числа у заданій системі зчислення, причому вважається, що
- цифри числа у заданій системі зчислення, причому вважається, що 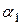 не дорівнює нулеві. Так, для десяткової системи зчислення
не дорівнює нулеві. Так, для десяткової системи зчислення  , порядок числа -
, порядок числа -  , кількість значущих десяткових розрядів -
, кількість значущих десяткових розрядів - 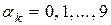 . Наприклад, для числа
. Наприклад, для числа  десятковий порядок дорівнює
десятковий порядок дорівнює  , кількість значущих розрядів
, кількість значущих розрядів  , а цифри
, а цифри
 .
. . Обсяг оперативній пам'яті ЕОМ, який віддається на запис поодинокого окремого числа, вимірюється у байтах (8 двійкових розряди - бітів) і залежить від мови програмування, на який записано програму, і типу числа, під яким його оголошено у програмі.
. Обсяг оперативній пам'яті ЕОМ, який віддається на запис поодинокого окремого числа, вимірюється у байтах (8 двійкових розряди - бітів) і залежить від мови програмування, на який записано програму, і типу числа, під яким його оголошено у програмі. до
до  . При цьому мантиса числа, маючи для запису 24 розряди, зберігає
. При цьому мантиса числа, маючи для запису 24 розряди, зберігає  десяткових розрядів числа. Тобто розглядуваний тип зберігає сім вірних десяткових цифр у кожному числі.
десяткових розрядів числа. Тобто розглядуваний тип зберігає сім вірних десяткових цифр у кожному числі. до
до  і з 7 вірними десятковими розрядами;
і з 7 вірними десятковими розрядами; до
до  з 12 вірними десятковими розрядами;
з 12 вірними десятковими розрядами; до
до  і з 16 вірними десятковими розрядами;
і з 16 вірними десятковими розрядами;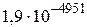 до
до  з 19 вірними десятковими розрядами.
з 19 вірними десятковими розрядами.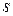 десяткових розрядів у запису мантиси у його поданні на ЕОМ:
десяткових розрядів у запису мантиси у його поданні на ЕОМ: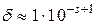 .
. , для того ж типу мови Паскаль
, для того ж типу мови Паскаль 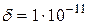 . Дані типу double у мові Паскаль і системі MatLAB мають елементарну похибку округлення
. Дані типу double у мові Паскаль і системі MatLAB мають елементарну похибку округлення . (2.7)
. (2.7)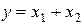 .
. у пам'ять ЕОМ; при цьому, навіть коли вихідне значення
у пам'ять ЕОМ; при цьому, навіть коли вихідне значення 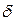 (це може бути, якщо точне значення величини містить більшу кількість десяткових розрядів, ніж
(це може бути, якщо точне значення величини містить більшу кількість десяткових розрядів, ніж 
 ;
;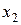 у пам'ять; це приводить до появи аналогічної похибки
у пам'ять; це приводить до появи аналогічної похибки 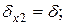
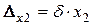 ;
;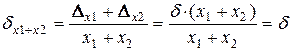 ;
; , а абсолютну похибку сумування можна оцінити за формулою
, а абсолютну похибку сумування можна оцінити за формулою  .
. ,
, знайдена перед цим
знайдена перед цим 
 ;
;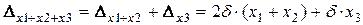 ;
;  ;
; ;
;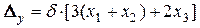 .
.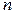 чисел
чисел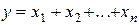
 ; (2.8)
; (2.8) .
.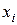 їхні абсолютні значення.
їхні абсолютні значення. ;
;  . Повторюючи попередні міркування, одержимо
. Повторюючи попередні міркування, одержимо . (2.9)
. (2.9)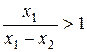 разів. Якщо віднімаються близькі величини, ця похибка може бути вельми значною.
разів. Якщо віднімаються близькі величини, ця похибка може бути вельми значною. ,
,  . Оцінимо похибку віднімання цих чисел.
. Оцінимо похибку віднімання цих чисел. , із формули (9) одержимо
, із формули (9) одержимо .
.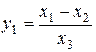 ;
;  .
. ;
;  ;
; ;
;  ;
; ;
; 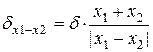 ;
; ;
;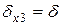 ;
; ;
;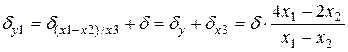 .
. ;
; 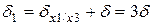 ;
;  ;
; ;
;  ;
;

 .
.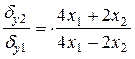 .
.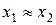 , то розрахунок за другою формулою приведе до похибки у 3 рази більшій, ніж розрахунок за першою формулою.
, то розрахунок за другою формулою приведе до похибки у 3 рази більшій, ніж розрахунок за першою формулою.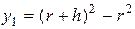 ;
; 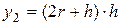 .
.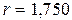 ;
;  . Відносні похибки вихідних даних покладемо рівними нулеві. Елементарну відносну похибку при округленні приймемо рівною
. Відносні похибки вихідних даних покладемо рівними нулеві. Елементарну відносну похибку при округленні приймемо рівною  .
. ;
; ;
;  ;
;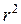 у пам'ять виникає похибка округлення
у пам'ять виникає похибка округлення 

 .
. у пам'ять
у пам'ять  ;
;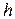 і занесення результату у пам'ять
і занесення результату у пам'ять 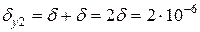 .
.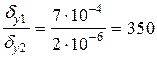 .
.




