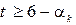Основні параметри: стан і ансамблі.
У основі моделювання лежить певна модель фізичної системи, в розрахунку характеристики якої ми зацікавлені. Ці характеристики одержують як середні по простору станів системи. Позначимо стан системи як x=(x1.xn), де n- число мір свободи. Безліч станів системи складають доступний їй фазовий простір W.
Систему можна описати, задаючи її мікроскопічний стан (мікростан). Такий опис дає нам найповнішу, відповідну законам механіки характеристику кожної частинки системи.
У більшому масштабі макроскопічний стан (макростан) системи можна описати за допомогою середніх концентрацій, температури, об'єму і т.д.
На відміну від непередбачуваного мікростану системи, макростан системи через деякий час перестає змінюватися. Такий стан називають рівноважним.
Якщо макростан ізольованої системи характеризується величинами N - число частинок, V - об'ємом і Е - енергією, то на мікроскопічному рівні в загальному випадку існує величезна кількість способів конфігурації, в яких може реалізуватися даний макростан (N, V, E).
Конкретний мікростан (конфігурація) є досяжним, якщо його характеристики відповідають даному макростану. У нас немає причин віддати пріоритет тому або іншому стану; і можна стверджувати, що у будь-який момент система рівномірно знаходитися в одному з своїх досяжних мікростанів (постулат рівної апріорної вірогідності).
Якщо ізольована система має W досяжних рівномірних станів, то вірогідність знайти її в мікростані S складає:
PS= 
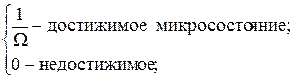
З погляду усереднювання за часом, фізичний сенс вірогідності PS - відрізок часу, протягом якого одна система знаходиться в мікростані S щодо всього часу спостереження.
Ансамбль, який характеризується величинами N, V, E і описується розподілом рівних апріорних імовірностей називають мікроканонічним.
У реальних (лабораторних) умовах система не замкнута, а знаходиться в тепловому контакті з навколишнім середовищем (формально - з тепловим резервуаром). Оскільки нас цікавлять рівноважні значення фізичних величин, то потрібно знати вірогідність Pl, з якою система знаходиться в стані S з енергією El. Ансамбль, який характеризується постійними величинами N, V, T і описується канонічним розподілом Гіббса:
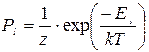
називається канонічним.
Тут z- статистична сума.
Завдання про гармонійний осцилятор .
Метод молекулярної динаміки (МД) обчислює характеристики системи, використовуючи рівняння руху. На ПК ми чисельно вирішуємо рівняння руху, і для цього апроксимуємо їх відповідною чисельною схемою, зручною для розрахунків на ПК.
Визначення:
Метод МД розраховує у фазовому просторі траєкторії сукупності молекул, кожна з яких підкоряється класичним рівнянням руху.
Елементарний приклад - завдання про коливання тіла, рухомого під дією пружної сили - одновимірний гармонійний осцилятор.
Ми задаємо гамільтоніан, який описує рух тіла під дією пружної сили:
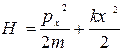 ;
;
далі, використовуючи закони класичної механіки і розкладання в ряд Тейлора:
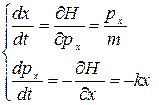
можна вивести рекурсивні формули для положення тіла і його імпульсу.
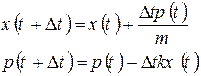
при цьому безперервна траєкторія руху замінюється ламаною лінією з кроком t.
Ми бачимо, що метод МД - детерміністичний: результат, одержаний на визначеному кроці визначається результатом, одержаним на попередньому кроці.
Чисельний алгоритм методу МД .
Нехай у нас є система з N частинок, і рух кожною описується диференціальними рівняннями:
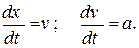
Нам потрібно згенерувати траєкторію у фазовому просторі, тобто підрахувати значення 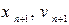 кожної частинки (їх сукупність дає нам точку у фазовому просторі) у момент часу:
кожної частинки (їх сукупність дає нам точку у фазовому просторі) у момент часу:
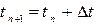 .
.
Типовим методом чисельного рішення диференціальних рівнянь є їх перетворення в кінцево-різницеві.
Замінимо похідну 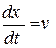 відношенням малого приросту функції до приросту аргументу (переміщення x за час t)
відношенням малого приросту функції до приросту аргументу (переміщення x за час t) 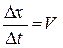 ?. Тобто для даної частинки в кожен момент часу tn+1 швидкість Vn+1:
?. Тобто для даної частинки в кожен момент часу tn+1 швидкість Vn+1:
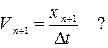 .
.
Значить, кожне наступне положення визначається через попереднє.
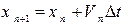
застосувавши ці міркування до диференціального рівняння, одержимо формули Ейлера для знаходження швидкості і координати, як рішення диференціальних рівнянь:
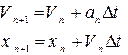
Припущенням цих формул, як ми бачимо, є те, що на відрізку (t n, tn+1) швидкість зміни функції X постійна. Метод Ейлера є асиметричним - він просуває рішення на 1 крок за часом t, використовуючи при цьому інформацію про похідні тільки в початковій точці інтервалу.
Існують точніші методи:
Метод Ейлера - Камера (метод приблизно по останній точці)
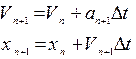
Метод середньої точки - використовує для нового значення координати середню на відрізку швидкість
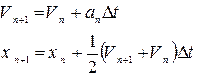
Метод напівкроку - використовує допущення, що швидкість на відрізку рівна значенню швидкості в середній точці відрізка
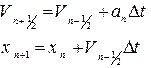
Можна порахувати:
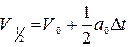
 .
.
Точнішим є метод Верне.
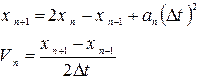
Недолік: необхідність іншого методу для отримання перших точок фазового простору і обчислення швидкості шляхом віднімання близьких за величинами значень. При цьому втрачаються значущі цифри, і росте помилка.
Ці недоліки відсутні в швидкісній формі алгоритму Верне.
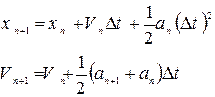
Метод Лиману і Шофілда:
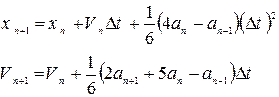
Вважається кращим за алгоритм Верне, оскільки краще зберігає енергію.
Метод предіктор - коректор - використовує "передбачення" нового значення координати.
Предіктор: 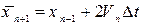 дозволяє обчислити прискорення, використовуючи яке знаходимо скоректовані значення:
дозволяє обчислити прискорення, використовуючи яке знаходимо скоректовані значення:
Коректор: 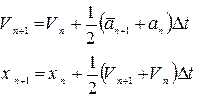
Скоректоване значення 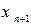 використовується для обчислення значення, що передбачаються, а значить - нових значень, що передбачаються
використовується для обчислення значення, що передбачаються, а значить - нових значень, що передбачаються 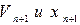 . Ця процедура повторюється до тих пір, доки значення, що передбачаються і скоректовані, не будуть близькі.
. Ця процедура повторюється до тих пір, доки значення, що передбачаються і скоректовані, не будуть близькі.
Метод Рунге- Кутта дозволяє підвищити точність методу Ейлера внаслідок екстраполяції в середній точці відрізка, а потім використовувати центральну похідну на всьому відрізку (див. курс Чисельні методи).
Для різних динамічних систем слід експериментувати з різними алгоритмами розрахунку. Однозначних переваг не має жоден метод.
5. Модель ідеального газу
На минулому занятті ми розглянули основну ідею детерміністичного методу МД, для того, щоб ми могли реалізувати на комп'ютері моделі ідеального і реального газів і досліджувати їх поведінку.
Мета дослідження моделей - перевірка основних газових законів і дослідження флуктуацій ідеального і реального газів.
Методи дослідження для моделі ідеального газу - методи МК і МД, для моделі реального газу - метод МД.
Нагадаємо, що в ідеальному газі можна нехтувати взаємодією між молекулами.
Модель ідеального газу .
У запропонованій моделі рух молекул задається у вигляді одновимірних блукань, при яких через рівні проміжки часу t (середній час між зіткненнями) швидкості змінюються випадково за допомогою генератора випадкових чисел згідно із законом:
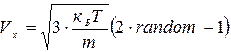 . (1)
. (1)
Тут середній квадрат випадкової функції
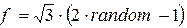
рівний одиниці, що забезпечує співвідношення:
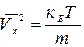 відоме з молекулярно-кінетичної теорії.
відоме з молекулярно-кінетичної теорії.
Співвідношення (1), тобто заміна максвелівського розподілу по Vx рівномірним із збереженням середнього квадрата є основним наближенням моделі.
Подальша процедура адекватна реальній ситуації. Кожне зіткнення із стінкою і переданий нею імпульс підраховується і підсумовується
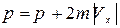
а молекули, що зіткнулися із стінкою, рухаються по законам пружного зіткнення. Наприклад, якщо координата молекули 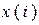 виявляється більше координати правої стінки L, то виконується привласнення
виявляється більше координати правої стінки L, то виконується привласнення
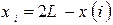
Тиск газу обчислюється за формулою 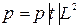 .
.
Величина P зазнає флуктуацій, але із збільшенням часу (і числа ударів) стає асимптотою. Фактично можна зупинитися після 6 кроків для всіх молекул, при 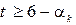
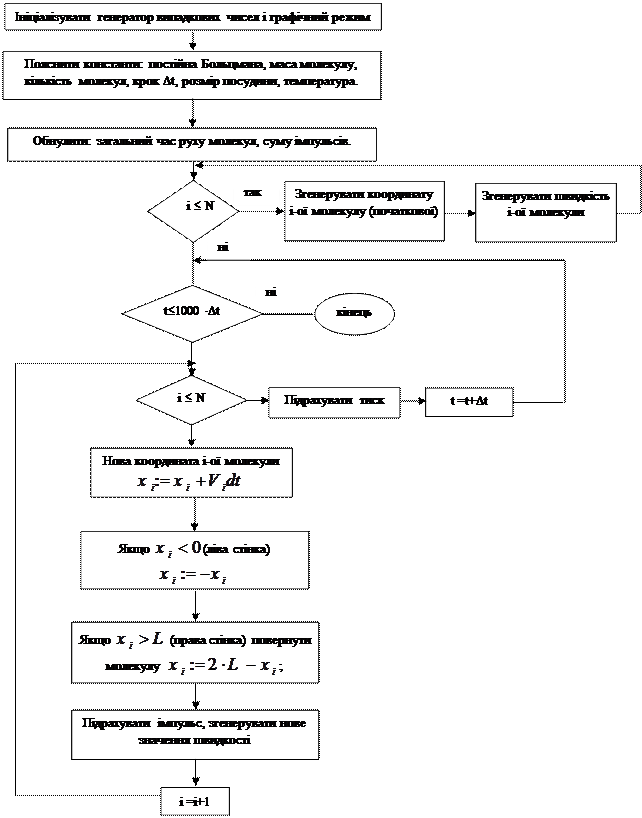
Алгоритм






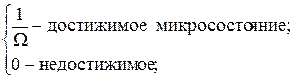
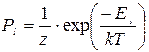
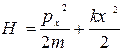 ;
;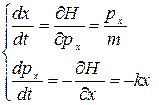
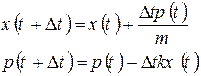
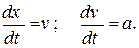
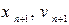 кожної частинки (їх сукупність дає нам точку у фазовому просторі) у момент часу:
кожної частинки (їх сукупність дає нам точку у фазовому просторі) у момент часу: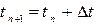 .
.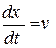 відношенням малого приросту функції до приросту аргументу (переміщення x за час t)
відношенням малого приросту функції до приросту аргументу (переміщення x за час t) 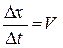 ?. Тобто для даної частинки в кожен момент часу tn+1 швидкість Vn+1:
?. Тобто для даної частинки в кожен момент часу tn+1 швидкість Vn+1: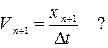 .
.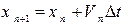
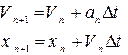
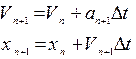
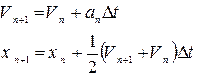
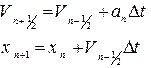
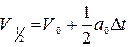
 .
.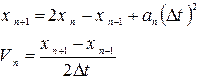
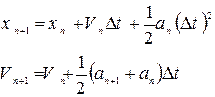
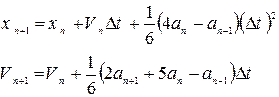
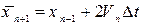 дозволяє обчислити прискорення, використовуючи яке знаходимо скоректовані значення:
дозволяє обчислити прискорення, використовуючи яке знаходимо скоректовані значення: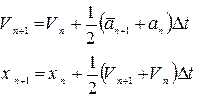
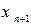 використовується для обчислення значення, що передбачаються, а значить - нових значень, що передбачаються
використовується для обчислення значення, що передбачаються, а значить - нових значень, що передбачаються 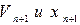 . Ця процедура повторюється до тих пір, доки значення, що передбачаються і скоректовані, не будуть близькі.
. Ця процедура повторюється до тих пір, доки значення, що передбачаються і скоректовані, не будуть близькі.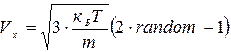 . (1)
. (1)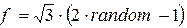
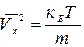 відоме з молекулярно-кінетичної теорії.
відоме з молекулярно-кінетичної теорії.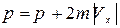
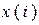 виявляється більше координати правої стінки L, то виконується привласнення
виявляється більше координати правої стінки L, то виконується привласнення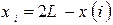
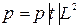 .
.