Дії над наближеними числами приводять до поширення похибок. Для оцінки похибок результатів потрібно знати похибки вихідних чисел і правила обчислення похибки результату. Розглянемо ці правила.
Похибки підсумовування
Неважко впевнитися у слушності наступних тверджень.
Абсолютна похибка суми й різниці дорівнює сумі абсолютних похибок доданків
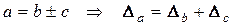 . (2.1)
. (2.1)
Відносна похибка суми двох величин однакового знаку перебуває в інтервалі між найменшою й найбільшою відносними похибками доданків
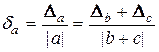 .
.
За умови 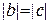 матимемо
матимемо 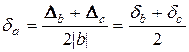 .
.
Якщо ж 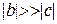 , через що останнім доданком у знаменнику можна знехтувати, то
, через що останнім доданком у знаменнику можна знехтувати, то
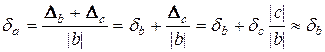 .
.
Подамо вираз для відносної похибки у такий спосіб
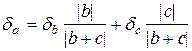 .
.
З його розгляду випливає наступне.
Додавання величин протилежного знаку (або віднімання величин однакового знаку) практично завжди приводить до збільшення відносної похибки результату у порівнянні з найбільшою з відносних похибок доданків.
Особливо небезпечним є віднімання дуже близьких величин. У цьому випадку відносна похибка результанта може сягати неприпустимих величин.
Приклад. Треба обчислити площу кругового тонкого кільця із внутрішнім радіусом 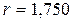 і товщиною
і товщиною 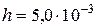 за формулою
за формулою 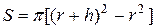 або
або 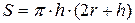 . Відшукати похибки.
. Відшукати похибки.
РОЗВ'ЯЗУВАННЯ
Перш за все потрібно зазначити, що, як випливає з угоди про форму запису наближеного числа, абсолютні похибки вихідних даних є такими:
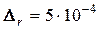 ;
; 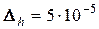 ,
,
а відносні похибки
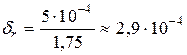 ;
; 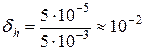 .
.
Розрахунки згідно першої формули приводять до таких похибок:
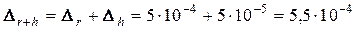 ;
;
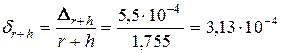 ;
;
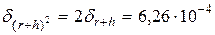 ;
;
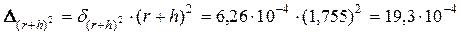 ;
;
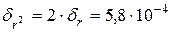 ;
;
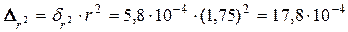 ;
;
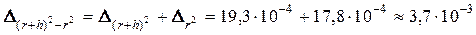 ;
;
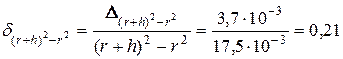 .
.
Якщо ж скористатися другою формулою, то одержимо такі похибки:
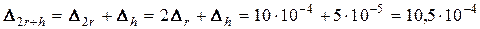 ;
;
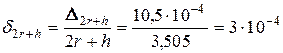 ;
;
 ;
;
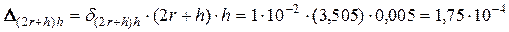 ;
;
Як бачимо
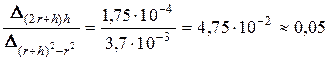 ,
,
тобто підрахунок за другою формулою дає змогу одержати результат у 21 рази точніший, ніж розрахунок за першою формулою, де відбувається віднімання близьких за значенням величин.
Наведений приклад засвідчує, що похибка результату залежить від порядку проведення обчислень і це потрібно враховувати при розрахунках. Алгебрично наведені формули тотожні, але для проведення обчислень кращою є друга. У першій формулі при відніманні близьких величин 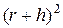 і
і 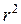 різко збільшується відносна похибка.
різко збільшується відносна похибка.





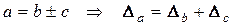 . (2.1)
. (2.1)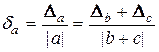 .
.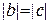 матимемо
матимемо 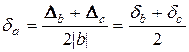 .
.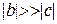 , через що останнім доданком у знаменнику можна знехтувати, то
, через що останнім доданком у знаменнику можна знехтувати, то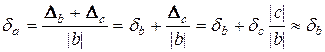 .
.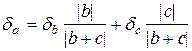 .
.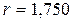 і товщиною
і товщиною 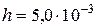 за формулою
за формулою 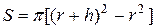 або
або 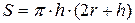 . Відшукати похибки.
. Відшукати похибки.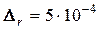 ;
; 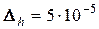 ,
,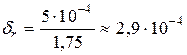 ;
; 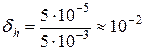 .
.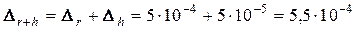 ;
;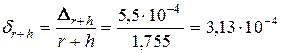 ;
;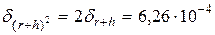 ;
;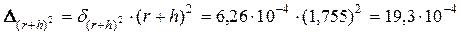 ;
;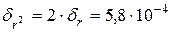 ;
;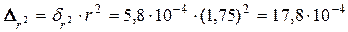 ;
;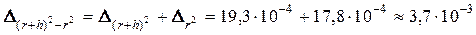 ;
;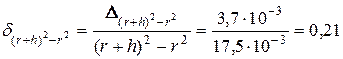 .
.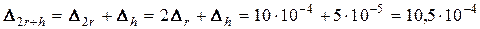 ;
;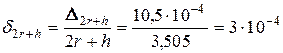 ;
; ;
;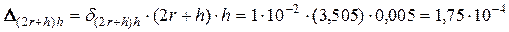 ;
;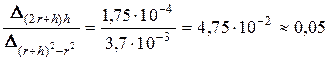 ,
,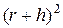 і
і 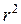 різко збільшується відносна похибка.
різко збільшується відносна похибка.


