Міністерство освіти і науки України
Національний технічний університет України
„Київський політехнічний інститут”
Методичні вказівки до практичних та лабораторних
занять “Обчислювальна фізика”
Навчально-методичний посібник для студентів
Напрямків підготовки (спеціальностей)
7.090102 “фізичне матеріалознавство”
Інженерно-фізичного факультету
Укладач: ст. викладач кафедри фізики металів Холмська Г.Д
Киів 2007
ЗМІСТ
1. Етапи розв'язування задач моделювання. Постановка задачі. Створення математичної моделі. Математичне моделювання.
2. Організація наближених обчислень. Джерела і види похибок. Запис наближених чисел. Правило округлення. Похибки результату при діях із наближеними числами. Поширення похибок округлення при обчисленнях.
3. Класифікація комп‘ютерних моделей. Детерміновані та стохастичні моделі і підходи до моделювання.
4. Модель випадкових блукань. Алгоритм. Параболічний закон дифузії. Генератори випадкових чисел, властивості ГВЧ .
5. Випадкові блукання та розподіл ймовірностей. Постановка задачі. Алгоритм випадкових блукань вакансії в металі.
6. Метод молекулярної динаміки. Стани та ансамблі. Усереднення по часу та по ансамблю частинок. Задача про гармонічний осцилятор. Числовий алгоритм метода молекулярної динаміки. Методи розв‘язання диференційних рівнянь руху.
7. Одновимірна модель ідеального газу. Числовий алгоритм.
8. Модель твердих сфер. Алгоритм. Побудова розподілу Максвела.
9. Метод Монте-Карло. Перевірка закону Ома на моделі одновимірних блукань електронів в електричному полі. Опис моделі, алгоритм. Перевірка закону Джоуля-Ленца.
10. Динаміка електронного газу. Ефект Хола. Модель та алгоритм реалізації розрахунків.
11. Елементи динаміки кристалічної гратки. Поняття про нормальні коливання. Модель одноатомного ланцюжка. Алгоритм числової реалізації на ЕОМ.
12. Магнітні властивості тіл. Парамагнетики. Двовимірна модель парамагнетика. Дослідження моделі процесу намагнічування парамагнетика. Модифікація моделі для перевірки Закону Кюрі.
13. Модель феромагнетика. Дослідження моделі процесу намагнічування феромагнетика. Алгоритм моделі для комп‘ютерного експерименту.
14. Розв‘язання рівняння дифузії методом молекулярної динаміки. Алгоритм числової реалізації.
15. Контрольні питання
16. Список використаної та рекомендованої літератури
Етапи розв'язування задач моделювання
Моделювання
Моделювання є основою пізнання людиною навколишнього світу. Проводячи експерименти, теоретичні дослідження, навіть обговорювання власних дій, намірів, висновків, ми практично займаємось моделюванням. Цілі, задачі, засоби й методи моделювання у цих випадках значно відрізняються один від одного, але загальна спрямованість залишається єдиною - одержання нового знання шляхом випробування (дослідження) деякого замінника реального об'єкта дослідження - моделі. У випадку експериментальних досліджень моделлю є реальний об'єкт, який має ту саму фізичну природу, що і досліджуваний об'єкт. При теоретичних дослідженнях модель має знакову форму - математичних формул, співвідношень, рівнянь, а задачею моделювання є встановлення нових знань про об'єкти, що описуються цими співвідношеннями. Обговорення встановлює слушність тих припущень і висновків, які були зроблені, шляхом моделювання, відношення до них досвідчених співрозмовників.
Взагалі, спрощено, моделювання можна розглядати як певний експеримент, об'єктом якого у першому випадку є матеріальний аналог досліджуваного об'єкта, у другому випадку об'єктом іспитів є знакова (математична) модель, у третьому - відношення до моделі, яка обмірковується, з боку громади.
Результатом розв'язування інженерних (прикладних) задач будь-якого рівня є, як правило, чисельні оцінки (параметрів пристроїв, процесів, технічних і економічних характеристик, тощо), які є наслідком розрахунків, що здійснюються з наближеними первісними даними. Більшість прикладних задач зводяться до математичних задач, які розв'язуються різноманітними обчислювальними методами.
Послідовність розв'язуванні таких задач можна подати у виді наступних етапів:
1) постановка задачі;
2) створення математичної моделі (формулювання задачі); перевірка моделі на адекватність;
3) побудова розрахункової (обчислювальної) моделі, яка відповідає прийнятій математичній моделі;
4) проведення розрахунків за обраною обчислювальною моделлю при заданих (відомих) значеннях первісних даних;
5) аналіз одержаних результатів.
У цілому процес розв'язування інженерної задачі може бути поданий у вигляді схеми, наведеної на рис. 1.1.
Розглянемо докладніше кожний з цих етапів.
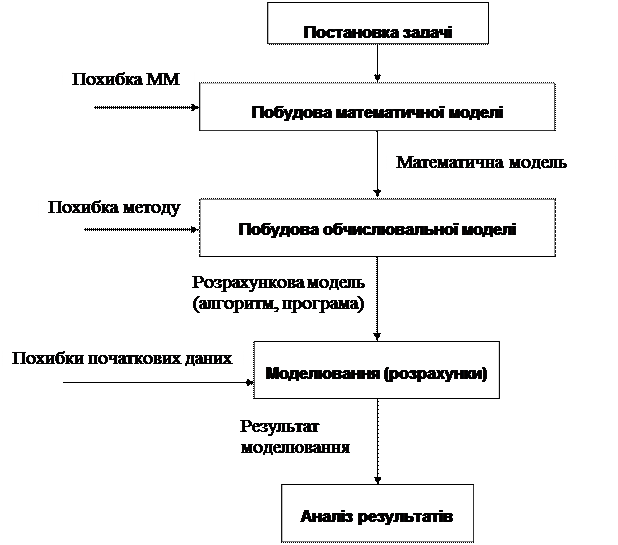
Рис. 1.1. Схема розв'язування інженерної задачі
Постановка задачі
Постановка задачі має передумовою словесне, змістовне формулювання задачі, умов, за яких вона ставиться, та вимог до її розв'язування. Слова "змістовне формулювання" слід розуміти так, що задача має бути сформульована у термінах опису реального об'єкта (технічного пристрою або процесу), поводження якого підлягає вивченню.
Як приклади розглянемо такі найпростіші інженерні задачі.
Задача 1. Визначити характеристики власного руху фізичного маятника за умови, його коливання малі.
Задача 2. Визначити змінення швидкості тіла при його падінні, враховуючи опір оточуючого середовища.
Задача 3. Знайти момент інерції ротора гіроскопа.
Задача 4. Визначити характеристики власного руху гіроскопа у кардановому підвісі, а також характеристики його вимушеного руху під дією моментів зовнішніх сил, що діють по осях карданового підвісу і змінюються з часом за гармонічним законом.
Створення математичної моделі
Математична модель - це математичний опис співвідношень постановки задачі. Такий опис можливий лише на основі попередньо одержаних знань про поводження об'єкта, що вивчається, і про способи правильного й ефективного опису цього поводження у математичних термінах. В одних випадках утворення математичної моделі не викликає труднощів (наприклад, модель є відомою за результатами раніше проведених досліджень), а в інших потрібно неодноразове уточнення постановки задачі, виділення головних визначальних чинників, відкидання чинників, які незначно впливають на результат і т.д..
Так, для задачі 1 математична модель може бути створена, якщо врахувати наступні теоретичні відомості.
1. До характеристик власного руху коливальної частинки, якою є фізичний маятник, відносять:
1) частоту власних коливань;
2) коефіцієнт загасання цих коливань.
2. При малих відхиленнях від вертикалі рух маятника з достатньою точністю описується лінійним диференційним рівнянням другого порядку зі сталими коефіцієнтами:
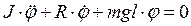 , (1.1)
, (1.1)
де 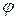 - кут відхилення маятника від вертикалі;
- кут відхилення маятника від вертикалі; 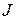 - момент інерції маятника відносно осі його обертання;
- момент інерції маятника відносно осі його обертання; 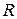 - коефіцієнт демпфірування;
- коефіцієнт демпфірування; 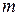 - маса маятника;
- маса маятника; 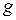 - прискорення вільного падіння;
- прискорення вільного падіння; 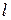 - зміщення центра мас маятника відносно осі його обертання;
- зміщення центра мас маятника відносно осі його обертання; 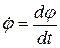 - кутова швидкість повороту маятника навколо його осі обертання;
- кутова швидкість повороту маятника навколо його осі обертання; 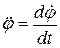 - кутове прискорення маятника.
- кутове прискорення маятника.
3. Власний рух маятника описується співвідношенням
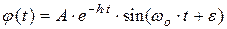 , (1.2)
, (1.2)
де 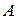 - початкове значення амплітуди власних коливань і
- початкове значення амплітуди власних коливань і 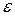 - початкова фаза власних коливань визначаються початковими умовами руху маятника, а
- початкова фаза власних коливань визначаються початковими умовами руху маятника, а 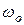 - частота власних коливань та
- частота власних коливань та 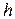 - коефіцієнт загасання власних коливань - це параметри, які визначаються лише параметрами самого маятника і не залежать від інших чинників. Фактично
- коефіцієнт загасання власних коливань - це параметри, які визначаються лише параметрами самого маятника і не залежать від інших чинників. Фактично 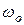 і
і 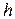 є шуканими величинами.
є шуканими величинами.
4. Величини 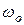 і
і 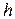 є відповідно уявною і дійсною частинами пари комплексно спряжених коренів характеристичного рівняння
є відповідно уявною і дійсною частинами пари комплексно спряжених коренів характеристичного рівняння
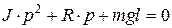 , (1.3)
, (1.3)
яке випливає з диференційного рівняння (1), тобто корінь рівняння (3) має вигляд:
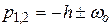 . (1.4)
. (1.4)
У підсумку математично розв'язування задачі 1 зводиться до пошуку комплексних коренів квадратного рівняння (3) і виділенню їхніх дійсної та уявної частин за заданими початковими даними - значеннями параметрів 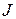 ,
, 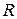 та
та 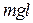 .
.
У задачі 2 треба припустити, що тіло є матеріальною точкою маси 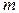 , з'ясувати під дією яких сил відбувається падіння тіла, визначити чинники, що впливають на силу опору, встановити залежність сили опору від цих факторів. Якщо вважати, що на тіло діють сила тяжіння
, з'ясувати під дією яких сил відбувається падіння тіла, визначити чинники, що впливають на силу опору, встановити залежність сили опору від цих факторів. Якщо вважати, що на тіло діють сила тяжіння 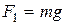 та сила опору, що є пропорційною до швидкості
та сила опору, що є пропорційною до швидкості 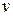 падіння, тобто
падіння, тобто 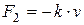 , то, на основі законів механіки одержимо рівняння
, то, на основі законів механіки одержимо рівняння 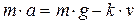 , або
, або
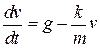 . (1.5)
. (1.5)
Це диференційне рівняння із врахуванням початкової умови 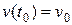 і є математичною моделлю задачі.
і є математичною моделлю задачі.
У задачі 3 насамперед слід з'ясувати форму ротора, його розміри, розподіл мас, потім виділити у тілі ротора ряд частин, знаходження моментів інерції яких робиться досить просто (циліндри, кільця, конуси тощо). Тоді задача зводиться до обчислень моментів інерції окремих елементарних тіл і їхньому сумуванню. Формули обчислення моментів інерції окремих частин ротора і їх додавання і складуть математичну модель цієї задачі.
Постановка задачі 4 має містити опис власних параметрів системи "гіроскоп у кардановому підвісі", опис параметрів зовнішніх моментів сил, опис рівнянь руху. Наприклад, рівняння руху гіроскопа для цієї задачі можуть бути взяті у наступному вигляді:
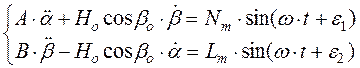 . (1.6)
. (1.6)
де 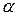 і
і 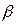 - кути повороту гіроскопа навколо осей підвісу;
- кути повороту гіроскопа навколо осей підвісу; 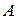 та
та 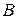 - його моменти інерції,
- його моменти інерції, 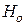 - власний кінетичний момент гіроскопа,
- власний кінетичний момент гіроскопа, 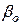 - початкове значення кута
- початкове значення кута 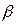 ;
; 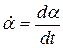 ;
; 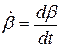 ;
; 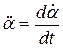 ;
; 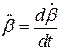 ;
; 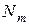 ,
, 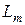 - амплітуди змінювання моментів зовнішніх сил;
- амплітуди змінювання моментів зовнішніх сил; 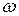 - частота цього змінювання;
- частота цього змінювання; 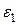 ,
, 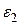 - початкові фази коливань цих моментів.
- початкові фази коливань цих моментів.
За математичну модель у цьому випадку можна брати сукупність розв'язків рівнянь (6), наведена нижче:
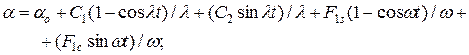
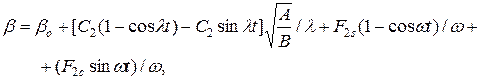 (1.7)
(1.7)
де 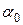 і
і 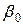 - початкові значення кутів визначаються
- початкові значення кутів визначаються 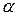 і
і 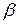 ;
; 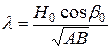 - частота власних (нутаційних) коливань гіроскопа;
- частота власних (нутаційних) коливань гіроскопа; 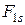 ,
, 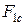 ,
, 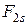 ,
, 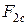 ,
, 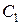 ,
, 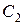 визначаються сукупністю співвідношень:
визначаються сукупністю співвідношень:
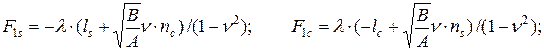
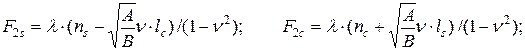
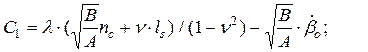
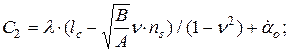
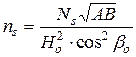 ;
; 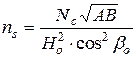 ;
; 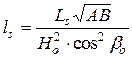 ;
; 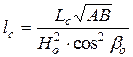 ;
;
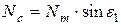 ;
; 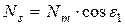 ;
; 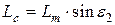 ;
; 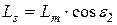 ;
;
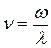 - відносна частота коливань моментів сил;
- відносна частота коливань моментів сил; 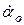 і
і 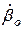 - початкові значення кутових швидкостей
- початкові значення кутових швидкостей 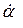 і
і 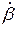 .
.
Рух гіроскопа за цими співвідношеннями може бути визначений у довільний момент часу. Але як математичну модель можна також розглядати і первісну систему диференційних рівнянь (6) за вказаних початкових умов.
Складання математичної моделі у прикладній задачі є найбільш складним і відповідальним етапом розв'язування і потребує, окрім істотних знань у спеціальній області, також і математичних і теоретичних знань.
Вже на цьому етапі розв'язування прикладної задачі доводиться нехтувати багатьма реальними процесами, як такими, що незначно впливають на процеси, які вивчаються, абстрагуватися від впливу багатьох чинників. Інакше кажучи, навіть коректно утворена математична модель завжди неповно, лише наближено, відображає реальні процеси. Але при цьому вона набуває риси більшої ясності, прозорості, більш доступна вичерпному дослідженню (з того боку, що підлягає вивченню).
Математичне моделювання
Модель створюється для подальшого її дослідження з метою одержання нових знань про відповідний реальний об'єкт. Таке дослідження вже готової моделі називають моделюванням. Дослідження математичної моделі називатимемо математичним моделюванням.
Математична задача є абстрагованою від конкретної сутності задачі. Для її розв'язування створюються спеціальні обчислювальні методи, причому до тої самої математичної моделі можуть зводитися зовсім різні прикладні задачі.
Так, задача 1 звелася до розв'язування квадратного рівняння, яке може відображати характеристичне рівняння не тільки фізичного, але й математичного маятника, маси, яка з'єднана пружиною з корпусом (лінійного акселерометра), гіроскопічного тахометру і т. і.
Диференційне рівняння (5) у задачі 2 може бути моделлю і для багатьох інших задач (вивчення змінювання швидкості тіла у в'язкому середовищі, змінювання електричного струму у найпростішому електричному ланцюзі, змінювання швидкості репродукції бактерій тощо).
Для розв'язування задачі 3 потрібно обчислити низку визначених інтегралів. До обчислення визначених інтегралів приходять і при пошуку площ складних фігур, об'єму тіла або дуги плоскої кривої, розрахунках роботи змінної сили і у багатьох інших фізичних задачах.
Математична модель (7) задачі 4 може описувати не тільки поводження гіроскопу, але й будь-якої іншої системи, якщо диференційні рівняння руху останньої збігаються з рівняннями (6).






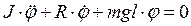 , (1.1)
, (1.1)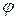 - кут відхилення маятника від вертикалі;
- кут відхилення маятника від вертикалі; 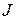 - момент інерції маятника відносно осі його обертання;
- момент інерції маятника відносно осі його обертання; 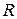 - коефіцієнт демпфірування;
- коефіцієнт демпфірування; 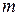 - маса маятника;
- маса маятника; 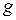 - прискорення вільного падіння;
- прискорення вільного падіння; 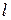 - зміщення центра мас маятника відносно осі його обертання;
- зміщення центра мас маятника відносно осі його обертання; 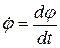 - кутова швидкість повороту маятника навколо його осі обертання;
- кутова швидкість повороту маятника навколо його осі обертання; 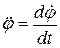 - кутове прискорення маятника.
- кутове прискорення маятника.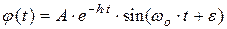 , (1.2)
, (1.2)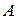 - початкове значення амплітуди власних коливань і
- початкове значення амплітуди власних коливань і 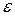 - початкова фаза власних коливань визначаються початковими умовами руху маятника, а
- початкова фаза власних коливань визначаються початковими умовами руху маятника, а 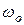 - частота власних коливань та
- частота власних коливань та 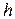 - коефіцієнт загасання власних коливань - це параметри, які визначаються лише параметрами самого маятника і не залежать від інших чинників. Фактично
- коефіцієнт загасання власних коливань - це параметри, які визначаються лише параметрами самого маятника і не залежать від інших чинників. Фактично 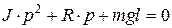 , (1.3)
, (1.3)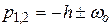 . (1.4)
. (1.4)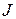 ,
, 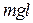 .
.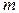 , з'ясувати під дією яких сил відбувається падіння тіла, визначити чинники, що впливають на силу опору, встановити залежність сили опору від цих факторів. Якщо вважати, що на тіло діють сила тяжіння
, з'ясувати під дією яких сил відбувається падіння тіла, визначити чинники, що впливають на силу опору, встановити залежність сили опору від цих факторів. Якщо вважати, що на тіло діють сила тяжіння 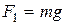 та сила опору, що є пропорційною до швидкості
та сила опору, що є пропорційною до швидкості 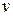 падіння, тобто
падіння, тобто 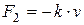 , то, на основі законів механіки одержимо рівняння
, то, на основі законів механіки одержимо рівняння 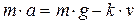 , або
, або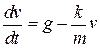 . (1.5)
. (1.5)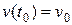 і є математичною моделлю задачі.
і є математичною моделлю задачі.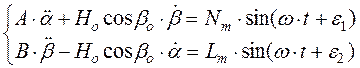 . (1.6)
. (1.6)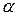 і
і 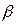 - кути повороту гіроскопа навколо осей підвісу;
- кути повороту гіроскопа навколо осей підвісу; 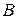 - його моменти інерції,
- його моменти інерції, 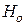 - власний кінетичний момент гіроскопа,
- власний кінетичний момент гіроскопа, 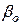 - початкове значення кута
- початкове значення кута 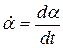 ;
; 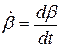 ;
; 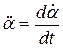 ;
; 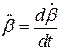 ;
; 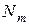 ,
, 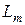 - амплітуди змінювання моментів зовнішніх сил;
- амплітуди змінювання моментів зовнішніх сил; 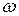 - частота цього змінювання;
- частота цього змінювання; 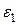 ,
, 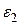 - початкові фази коливань цих моментів.
- початкові фази коливань цих моментів.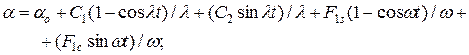
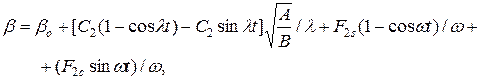 (1.7)
(1.7)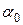 і
і 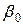 - початкові значення кутів визначаються
- початкові значення кутів визначаються 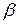 ;
; 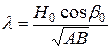 - частота власних (нутаційних) коливань гіроскопа;
- частота власних (нутаційних) коливань гіроскопа; 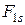 ,
, 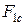 ,
, 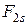 ,
, 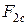 ,
, 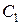 ,
, 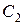 визначаються сукупністю співвідношень:
визначаються сукупністю співвідношень: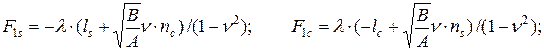
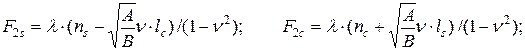
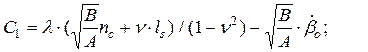
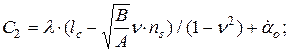
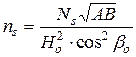 ;
; 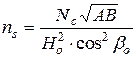 ;
; 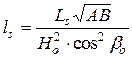 ;
; 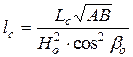 ;
; 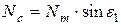 ;
; 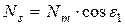 ;
; 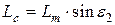 ;
; 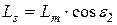 ;
;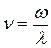 - відносна частота коливань моментів сил;
- відносна частота коливань моментів сил; 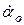 і
і 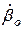 - початкові значення кутових швидкостей
- початкові значення кутових швидкостей 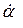 і
і 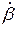 .
.


