Основним параметром є радіус молекул, які ми вважаємо твердими двомірними кулями (модель твердих сфер).
Метод розрахунку: МД тобто моменти результати зіткнень визначаються самою системою. Для цього підраховується час зіткнення всіх молекул між собою і стінками і вибирається найменше. Стінки можуть рухатися.
Алгоритм
Тестовий приклад :
T=10 K, число молекул N=20, R=1e-10м (радіус молекули), розміри посудини 1е-8м; маса - молекули кисню.
***до пункту 4.
а) DC:=Ci-j; DU:=Ui-j; DVx=Vxi-Vxj; DVy=Vyi-Vyj;
а: =DVx2+Vy2
b: =2×(DC×DVx+DU×DVy);
з: =DC2+DU2-4×R2;
d: =b2-4ac
б) якщо а=0 і b=0 або (а і d те t k:=-1;
в) якщо а=0 і b, то t k:=-cb;
г) якщо а то:
1) якщо d=0, то tk: =-b/(2×a)
2) якщо d>0, то t1: =(-b+ 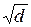 )/(2×/(2×а
)/(2×/(2×а
t2: =(-b- 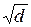 )/(2a),
)/(2a),
2.1) якщо t1t2, то tk: =t1=t2
д) знайти min час серед tk: tmol: =min(tk).
***до пункту 3
а) якщо Vxi>0, то t1: =(Lx-R-Xi)/Vxi
б) якщо Vxi<0, то t1: =(x0+R-xi)/(Vxi-Vst)
(x0 і Vst- координата і швидкість лівої стінки)
в) якщо Vyi>0, то t2: =(Ly-R-yi)/Vyi
г) якщо Vyi<0, то t2: =(R-yi)/Vyi
д) якщо t1<t2 те ti: =t1, інакше ti: =t2
е) знайти min серед ti: tst: =min(ti)
**** до пункту 6.
а) якщо dt=tst, то:
1) якщо CrVxrdt-R, то Vnx: =-Vxr+2×Vst інакше Vnx: =Vxr;
2) якщо Cr+Vxrdt+RLx, то Vnx: =-Vxr інакше Vnx: =Vxr
3) якщо Cr+Vxrdt+RLx, то Vnx: =-Vxr інакше Vnx: =Vxr
4) якщо Ur+Vyrdt-R£0; або Ur+Vyrdt+RLy, то Vny: =-Vyr, інакше Vny: =Vyr.
б) якщо dt=tmol, то
Cnk: =Ck+Vxkdt; Unk: =Uk+Vykdt
Cnl: =Cl+Vxldt; Unl: =Ul+Vyldt;
Sx=nl-nk; Sy: =Unl-Unk;
S= 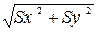 ;
;
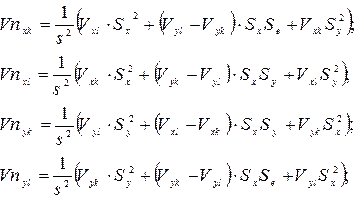
Завдання:
1. Досліджувати дію міжмолекулярних зіткнень на безповоротність.
Всі реальні процеси необоротні, що пов'язано з нестійкістю фазових траєкторій макросистем щодо малих збуджень. Якщо в якийсь момент змінити швидкості всіх молекул на протилежні, навіть мінімальне збудження не дасть їм рухатися "слід в слід" і опинитися в початковому мікростані. Якщо виконати це для попереднього алгоритму - моделі ідеального газу, то ми побачимо, що зіткнення з гладкими стінками матеріальних точок - молекул ідеального газу не вносить внесок до безповоротності процесу. Ця проблема вирішується в даному алгоритмі - моделі твердих сфер. Перевірити це практично.
2. Перевірити рівняння адіабати для двомірної моделі реального газу.
При включенні в модель повільного руху стінки можна досліджувати рівняння адіабати (Т(V)).
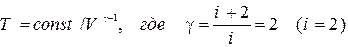
Температура розраховується через середній квадрат швидкості молекул.
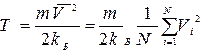
3. Побудувати розподіл Максвела:
а) знайти середньоквадратичну швидкість
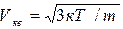
б) ввести умовну верхню межу швидкості
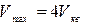
в) 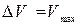 /20;
/20;
г) визначити, в який інтервал потрапляє швидкість кожної молекули і побудувати гістограму.
Це дає можливість простежити за кінетикою встановлення статистичної рівноваги. Якщо задати початкові швидкості однаковими за величиною і напрямом, у міру зіткнень гістограма з прямокутника перетвориться на розподіл Максвела.
Примітка: нагадаємо, що розподіл Максвела є окремий випадок розподілу Максвелла- Больцмана, коли нас, цікавить вірогідність швидкості або імпульсу молекул ідеального газу.
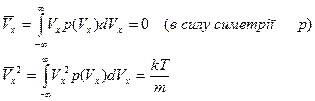
Перевірка закону Ома на моделі одновимірних блукань електронів в електричному полі з випадковими зіткненнями (МК - метод).
Фізична постановка завдання
Поведінка металу в електричному, тепловому або магнітному полях достатньо точно описується класичною електронною теорією Друзе-Лоренца (початок 20 століття).
Основні положення електронної теорії:
1. Метал складається з іонного каркаса і електронного газу: вільні електрони не пов'язані з конкретними іонами. Останні забезпечують нейтральність системи і не дають електронам розлітатися.
2. Рух електронів - поступальна хода вільних частинок між зіткненнями. При зіткненні електрон "забуває" передісторію.
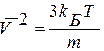 ; де T- температура в місці зіткнення.
; де T- температура в місці зіткнення.
3. Вірогідність зіткнення електрона впродовж малого часу dt пропорційна цьому часу і рівна
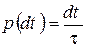 де
де
ђ- середній час вільного пробігу (час релаксації системи), а формула (2) справедлива при dt<<ђ (для більшості металів ђ =10-14с).
Знайдемо вірогідність того, що електрон не зазнає зіткнень впродовж часу t. Розіб'ємо весь часовий інтервал на відрізки 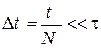 . Шукана вірогідність рівна добутку вірогідності на кожному відрізку:
. Шукана вірогідність рівна добутку вірогідності на кожному відрізку:
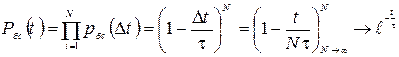
(згідно математичній формулі 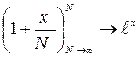 ).
).
Середній час до зіткнення:
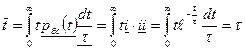 ; де
; де
i- вірогідність уникнути зіткнення впродовж t
ii- вірогідність зіткнення на наступному інтервалі dt.
Аналогічно: 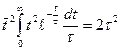 (звернемо увагу на множник 2)
(звернемо увагу на множник 2)
4. Згідно закону Ома, дія постійного електричного поля 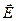 на метал діє постійний електричний струм, пропорційний середній швидкості зарядів. Тобто швидкість, а не прискорення пропорційно силі. Цей "парадокс" пояснюється зіткненнями електронів з тепловими і структурними дефектами, що необхідно враховувати в моделі через коефіцієнт електропровідності.
на метал діє постійний електричний струм, пропорційний середній швидкості зарядів. Тобто швидкість, а не прискорення пропорційно силі. Цей "парадокс" пояснюється зіткненнями електронів з тепловими і структурними дефектами, що необхідно враховувати в моделі через коефіцієнт електропровідності.
Зауваження*. Закон Ома в диференціальній формі:
Нехай на електрони газу в металі діє поле напруженості Е, тоді на кожен електрон діє зовнішня сила, тобто кожен електрон між зіткненнями повинен рухатися рівноприскорено.
Нехай t - час після останнього зіткнення;
V0- швидкість після останнього зіткнення.
Тоді: 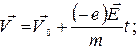 (3)
(3)
Середня швидкість: 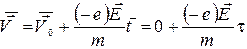 (4) тому:
(4) тому:
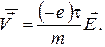 (5)
(5)
Щільність струму:
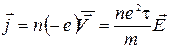 (6)
(6)
В результаті:
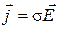 де
де 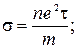 (7)
(7)
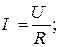 враховуючи, що
враховуючи, що 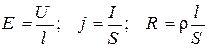
l - довжина провідника;
S - площа перетину.
Алгоритм
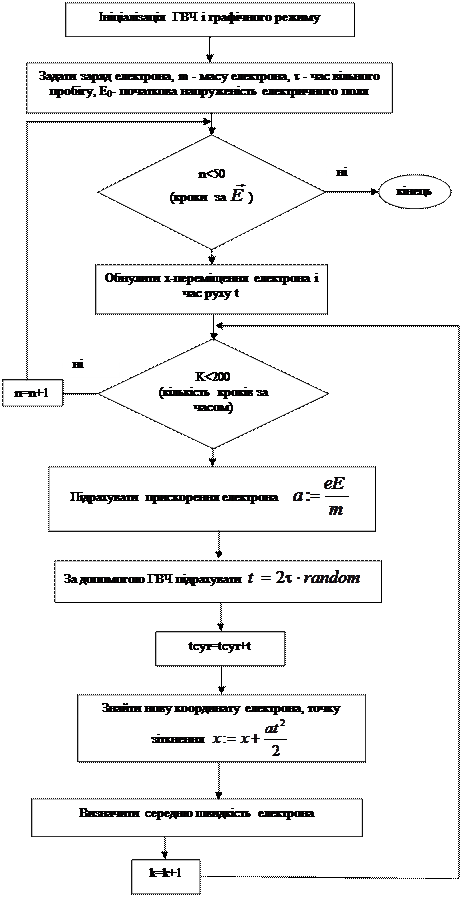
Тестовий приклад:
Е=0; DЕ=100 В/м; t=10-14 с.
Заняття 8.
Перевірка закону Джоуля - Ленца (метод МК)
Фізична модель:
Під час зіткнення електрони передають гратці свою енергію, одержану за рахунок їх прискорення зовнішнім полем. Знайдемо енергію, яка виділяється за одиницю часу в одиничному об'ємі. Даний об'єм знаходиться в електричному полі з напруженістю 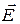 . Для цього знайдемо середню зміну енергії електрона під час зіткнення:
. Для цього знайдемо середню зміну енергії електрона під час зіткнення:
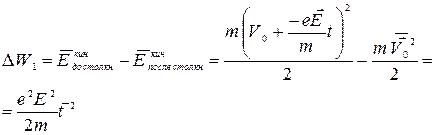
де 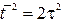 (дивись попереднє заняття).
(дивись попереднє заняття).
Отже:
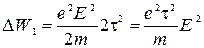 ;
;
звідси:
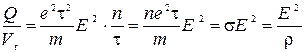 .
.
Чисельна модель.
У основу моделі покладено використання ГВЧ для часу між зіткненнями електронів з граткою.
Вважаємо, що у момент зіткнення електрон втрачає всю енергію, одержану від електричного поля.
Після усереднювання за великою кількістю зіткнень знаходимо середню енергію, яку електрон віддає кристалічній решітці за одиницю часу. Помноживши її на концентрацію електронів одержимо потужність теплових втрат за одиницю часу.






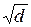 )/(2×/(2×а
)/(2×/(2×а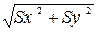 ;
;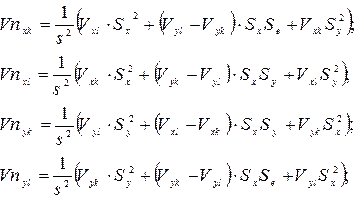
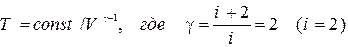
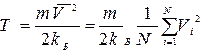
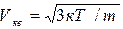
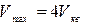
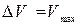 /20;
/20;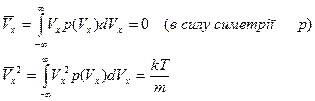
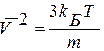 ; де T- температура в місці зіткнення.
; де T- температура в місці зіткнення.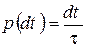 де
де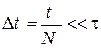 . Шукана вірогідність рівна добутку вірогідності на кожному відрізку:
. Шукана вірогідність рівна добутку вірогідності на кожному відрізку: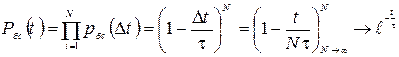
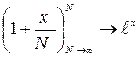 ).
).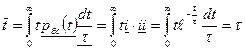 ; де
; де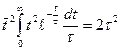 (звернемо увагу на множник 2)
(звернемо увагу на множник 2)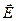 на метал діє постійний електричний струм, пропорційний середній швидкості зарядів. Тобто швидкість, а не прискорення пропорційно силі. Цей "парадокс" пояснюється зіткненнями електронів з тепловими і структурними дефектами, що необхідно враховувати в моделі через коефіцієнт електропровідності.
на метал діє постійний електричний струм, пропорційний середній швидкості зарядів. Тобто швидкість, а не прискорення пропорційно силі. Цей "парадокс" пояснюється зіткненнями електронів з тепловими і структурними дефектами, що необхідно враховувати в моделі через коефіцієнт електропровідності.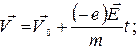 (3)
(3)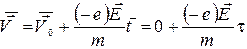 (4) тому:
(4) тому: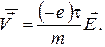 (5)
(5)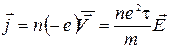 (6)
(6)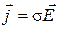 де
де 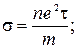 (7)
(7)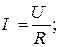 враховуючи, що
враховуючи, що 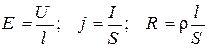

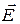 . Для цього знайдемо середню зміну енергії електрона під час зіткнення:
. Для цього знайдемо середню зміну енергії електрона під час зіткнення: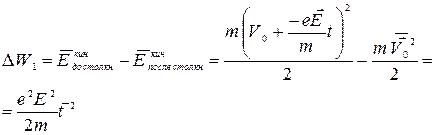
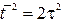 (дивись попереднє заняття).
(дивись попереднє заняття).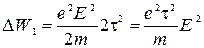 ;
;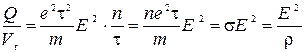 .
.


