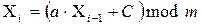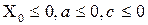Будь-якому реальному процесу властиві випадкові коливання, що викликаються фізичною мінливістю якихось чинників 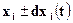 в часі. Крім того, можуть існувати випадкові зовнішні дії на систему. Тому при рівному середньому значенні вхідних параметрів
в часі. Крім того, можуть існувати випадкові зовнішні дії на систему. Тому при рівному середньому значенні вхідних параметрів 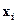 в різні моменти часу вихідні параметри будуть неоднакові. Отже, якщо випадкові дії на досліджувану систему істотні, необхідно розробляти імовірнісну (стохастичну) модель об'єкту, враховуючи статистичні закони розподілу параметрів системи і вибираючи відповідний математичний апарат.
в різні моменти часу вихідні параметри будуть неоднакові. Отже, якщо випадкові дії на досліджувану систему істотні, необхідно розробляти імовірнісну (стохастичну) модель об'єкту, враховуючи статистичні закони розподілу параметрів системи і вибираючи відповідний математичний апарат.
При побудові детермінованих моделей випадковими чинниками нехтують, враховуючи лише конкретні умови вирішуваної задачі, властивості і внутрішні зв'язки об'єкту (за цим принципом побудовані практично всі розділи класичної фізики)
Ідея детерміністичних методів - у використанні власної динаміки моделі при еволюції системи.
У нашому курсі ці методи представляють: метод молекулярної динаміки, перевагами якого є: точність і визначеність чисельного алгоритму; недоліком - трудомісткість через підрахунок сил взаємодії між частинками (для системи N частинок на кожному кроці потрібно виконати 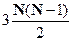 операцій підрахунку цих сил).
операцій підрахунку цих сил).
При детерміністичному підході задаються і інтегруються за часом рівняння руху. Ми розглядатимемо системи з багатьох частинок. Положення частинок дають внесок потенційної енергії в повну енергію системи, а їх швидкості визначають внесок кінетичної енергії. Система рухається уздовж траєкторії з постійною енергією у фазовому просторі (далі будуть пояснення). Для детермінованих методів природним є мікроканонічний ансамбль, енергія якого - це інтеграл руху. Крім того, можна досліджувати і системи, для яких інтегралом руху є температура і (або) тиск. В цьому випадку система незамкнута, і її можна представити у контакті з тепловим резервуаром (канонічний ансамбль). Для її моделювання можна використовувати підхід, при якому ми обмежуємо ряд мір свободи системи (наприклад, задаємо умову 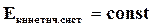 ).
).
Як ми вже відзначали, у разі, коли процеси в системі відбуваються непередбачувано, такі події і пов'язані з ними величини називають випадковими, а алгоритми моделювання процесів в системі - імовірнісними (стохастичними). Грецьке stoohastikos означає буквально “той, хто може вгадати”.
Стохастичні методи використовують декілька інший підхід, ніж детерміністичні: потрібно розрахувати лише конфігураційну частину завдання. Рівняння для імпульсу системи завжди можна проінтегрувати. Проблема, яка потім встає, - яким чином вести переходи від однієї конфігурації до іншої, які в детерміністичному підході визначаються імпульсом. Такі переходи в стохастичних методах здійснюються при імовірнісній еволюції в марківському процесі. Марківський процес є імовірнісним аналогом власної динаміки моделі.
Цей підхід має перевагу в тому, що дозволяє моделювати системи, що не мають власної динаміки.
На відміну від детерміністичних, стохастичні методи на ПК реалізуються простіше, швидше, проте для отримання близьких до істинних величин необхідна хороша статистика, що вимагає моделювання великого ансамблю частинок.
Прикладом повністю стохастичного методу є метод Монте-Карло.
Стохастичні методи використовують важливу концепцію марківського процесу (марківській ланцюг). Марківський процес є імовірнісним аналогом процесу в класичній механіці. Марківський ланцюг характеризується відсутністю пам'яті, тобто статистичні характеристики найближчого майбутнього визначаються тільки сьогоденням, без урахування минулого.
Модель випадкового блукання
Приклад (формальний)
Припустимо, що у вузлах двовимірних граток в довільних позиціях розміщені частинки. На кожному часовому кроці частинка “стрибає” в одну з найближчих позицій. Тобто частинка має можливість вибору напряму стрибка в будь-яке з чотирьох найближчих місць. Після стрибка частинка "не пам'ятає", звідки вона стрибнула. Цей випадок відповідає випадковому блуканню і є марківським ланцюгом. Результатом на кожному кроці є новий стан системи частинок. Перехід з одного стану в інший залежить тільки від попереднього стану, тобто вірогідність знаходження системи в стані i залежить тільки від стану i-1.
Які ж фізичні процеси в твердому тілі нагадують подібні до описаної моделі випадкового блукання?
Звичайно ж, дифузійні, тобто процеси, механізми яких ми розглядали у курсі тепло-масопереносу (3 курс). Як приклад пригадаємо звичайну класичну самодифузію в кристалі, коли, не міняючи своїх видимих властивостей атоми періодично міняють місця часової осідлості і блукають по гратці за допомогою “вакансійного” механізму. Він же - один з найважливіших механізмів дифузії в сплавах. Явище міграції атомів в твердих тілах грають вирішальну роль в багатьох традиційних і нетрадиційних технологіях - металургії, металообробці, створенні напівпровідників і надпровідників, захисних покриттів і тонких плівок.
Його відкрив Роберт Аустен в 1896 році, спостерігаючи дифузію золота і свинцю. Дифузія - процес перерозподілу концентрацій атомів в просторі шляхом хаотичної (теплової) міграції. Причини, з погляду термодинаміки, можуть бути дві: ентропійна (завжди) і енергетична (іноді). Ентропійна причина - це збільшення хаосу при перемішуванні атомів різного сорту. Енергетична - сприяє утворенню сплаву, коли вигідніше бути поряд атомам різного сорту, і сприяє дифузійному розпаду, коли енергетичний виграш, забезпечується розміщенням разом атомів одного сорту.
Найбільш поширеними механізмами дифузії є:
· вакансійний
· міжвузловий
· механізм витіснення
Сформуємо тепер модель випадкового блукання для явища дифузії в кристалі. Процес блукання атома - хаотичний і непередбачуваний. Проте для ансамблю блукаючих атомів повинні виявлятися статистичні закономірності. Ми розглянемо некорельовані стрибки.
Це означає, що якщо і - переміщення атомів при i і j-м стрибках, то після усереднювання по ансамблю блукаючих атомів.
Нехай кожна частинка ансамблю здійснює N елементарних стрибків. Тоді її повне переміщення рівне:
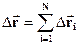 ;
;
а середній квадрат переміщення
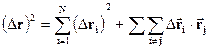
Оскільки кореляції немає, то другий доданок =0.
Хай кожен стрибок має однакову довжину h і випадковий напрям, а середнє число стрибків в одиницю часу - v. Тоді
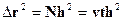
Очевидно, що 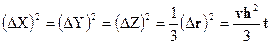

Назвемо величину - коефіцієнтом дифузії блукаючих атомів.
Тоді 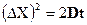 ;
;
Для тривимірного випадку - 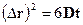 .
.
Ми одержали параболічний закон дифузії - середній квадрат зсуву пропорційний часу блукань.
Саме це завдання нам належить вирішити на наступній лабораторній роботі - моделювання випадкових одновимірних блукань.
Чисельна модель.
Ми задаємо ансамбль з М частинок, кожна з яких здійснює N кроків, незалежно один від одного, вправо або вліво з однаковою вірогідністю. Довжина кроку = h.
Для кожної частинки обчислюємо квадрат зсуву 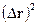 за N кроків. Потім проводимо усереднювання по ансамблю -
за N кроків. Потім проводимо усереднювання по ансамблю - 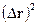 .
.
Алгоритм 1
Тестовий приклад:
M=1000; N=100; h=2.
Завдання:
1. Виконати алгоритм з урахуванням "вітру" (різна вірогідність кроків вправо, вліво і перевірити параболічний закон.
2. Модифікувати алгоритм для двомірного випадку (кроки вправо, вліво, вверх, вниз) і підрахувати середній квадрат зсуву, як x2+y2. Вивести на екран частинку.
Генератори випадкових чисел.
Звернемо увагу на 1 пункт алгоритму.
Для його реалізації необхідні випадкові числа.
Методи рішення задач, які використовують випадкові числа, називають стохастичними методами, або методами Монте-Карло. Простим генератором випадкових чисел є рулетка.
Проте через трудомісткість моделювання випадкових чисел, тільки з появою ЕОМ метод придбав широкого розповсюдження. Вважають, що він з'явився в 1949 році, а його автори - американці Дж. Нейман і С. Улам.
Наскільки хороші методи МК через їх стохастичну природу залежить від якості генератора випадкових чисел. Генератор повинен мати такі властивості:
1. Хороші стохастичні властивості
2. Ефективність
3. Великий період
4. Відтворюваність
Перший пункт - найбільш важливий. Насправді генерують не випадкові числа, а послідовність псевдовипадкових чисел. Всі генератори створюють такі послідовності за допомогою рекурентних співвідношень, використовуючи функцію залишку. Така послідовність через період повторює себе. Ефективність генератора важлива, оскільки потрібна велика кількість випадкових чисел (1010) + економія пам'яті.
Відтворюваність потрібна для того, щоб перевірити вплив змін в алгоритмі на результати моделювання випадкових чисел. Прикладом алгоритму отримання псевдовипадкових чисел може служити запропонований Дж. Нейманом метод середини квадратів. Чотиризначне число зводиться в квадрат, чотири внутрішні цифри знову в квадрат, і т.д. Випадковими приймаються чотирьохзначні числа 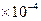 . Цей метод дає непропорційно багато малих значень.
. Цей метод дає непропорційно багато малих значень.
Найбільш популярні зараз лінійні конгруентні генератори.
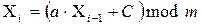

де 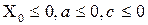





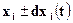 в часі. Крім того, можуть існувати випадкові зовнішні дії на систему. Тому при рівному середньому значенні вхідних параметрів
в часі. Крім того, можуть існувати випадкові зовнішні дії на систему. Тому при рівному середньому значенні вхідних параметрів 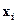 в різні моменти часу вихідні параметри будуть неоднакові. Отже, якщо випадкові дії на досліджувану систему істотні, необхідно розробляти імовірнісну (стохастичну) модель об'єкту, враховуючи статистичні закони розподілу параметрів системи і вибираючи відповідний математичний апарат.
в різні моменти часу вихідні параметри будуть неоднакові. Отже, якщо випадкові дії на досліджувану систему істотні, необхідно розробляти імовірнісну (стохастичну) модель об'єкту, враховуючи статистичні закони розподілу параметрів системи і вибираючи відповідний математичний апарат.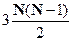 операцій підрахунку цих сил).
операцій підрахунку цих сил).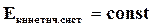 ).
).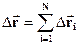 ;
;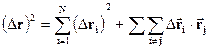
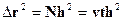
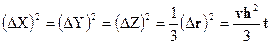

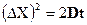 ;
;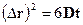 .
.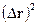 за N кроків. Потім проводимо усереднювання по ансамблю -
за N кроків. Потім проводимо усереднювання по ансамблю - 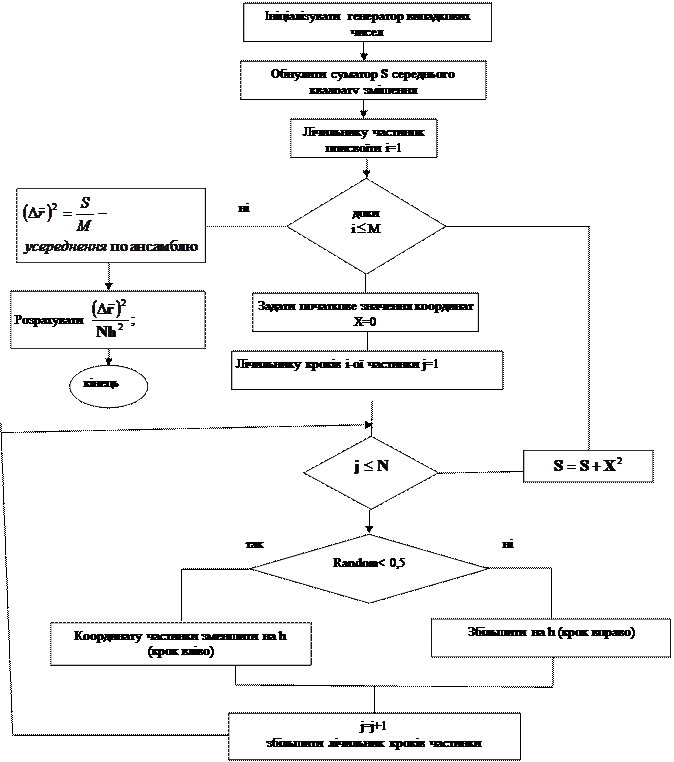
 . Цей метод дає непропорційно багато малих значень.
. Цей метод дає непропорційно багато малих значень.