5.1. Дві невеликі однакові заряджені кульки, кожна маси 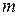 , підвішені в одній точці на умовно нерозтяжних нитках довжиною
, підвішені в одній точці на умовно нерозтяжних нитках довжиною 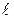 . Відстань між кульками
. Відстань між кульками 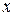 <<
<< 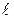 . Знайти швидкість стікання зарядів
. Знайти швидкість стікання зарядів  з кожної кульки, якщо швидкість їх зближення змінюється за законом
з кожної кульки, якщо швидкість їх зближення змінюється за законом 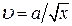 , де
, де 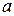 -стала.
-стала.
Розв’язування.

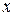 <<
<< 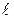 Умовно зафіксуємо миттєвий стан системи як рівноважний.
Умовно зафіксуємо миттєвий стан системи як рівноважний.

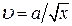 Оскільки система симетрична відносно вертикалі, що проходить
Оскільки система симетрична відносно вертикалі, що проходить
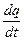 -? через точку підвісу, то доцільно розглянути сили, які діють на одну
-? через точку підвісу, то доцільно розглянути сили, які діють на одну
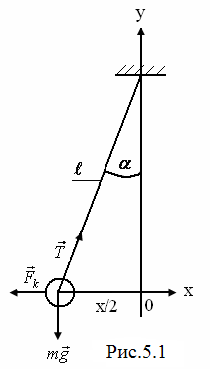
кульку (рис.5.1). У стані рівноваги векторна сума всіх цих сил дорівнює нулеві:
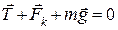 . (а)
. (а)
Тут 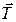 - реакція нитки,
- реакція нитки, 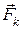 - кулонівська сила взаємодії між кульками,
- кулонівська сила взаємодії між кульками, 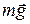 - сила тяжіння. Запишемо рівняння (а) у проекціях на координатні осі x та y:
- сила тяжіння. Запишемо рівняння (а) у проекціях на координатні осі x та y:
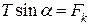 ;
; 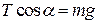 . (б)
. (б)
Сумісне рішення системи рівнянь (б) дає рівняння
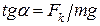 . (в)
. (в)
Оскільки 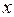 <<
<< 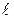 , то можна прийняти, що
, то можна прийняти, що 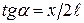 . Враховуючи закон Кулона, на підставі
. Враховуючи закон Кулона, на підставі 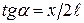 (в) отримуємо:
(в) отримуємо:
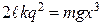 . (г)
. (г)
Продиференціювавши ліву та праву частини рівняння (г), маємо:
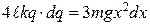 .
.
Прийнявши, що за малий проміжок часу 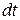 зближення кульок
зближення кульок 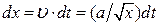 і враховуючи, що згідно з рівнянням (г)
і враховуючи, що згідно з рівнянням (г)
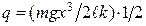 і що
і що 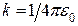 , знаходимо кінцеве рівняння у загальному вигляді:
, знаходимо кінцеве рівняння у загальному вигляді:
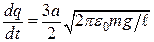 .
.
5.2. Три точкові однакові позитивні заряди 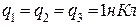 розміщені у вершинах рівностороннього трикутника (рис.5.2). Який негативний точковий заряд
розміщені у вершинах рівностороннього трикутника (рис.5.2). Який негативний точковий заряд 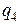 потрібно помістити в центр трикутника, щоб сила притягання з його боку зрівноважила сили взаємного відштовхування зарядів, які знаходяться у вершинах?
потрібно помістити в центр трикутника, щоб сила притягання з його боку зрівноважила сили взаємного відштовхування зарядів, які знаходяться у вершинах?


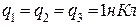 Розв’язування.
Розв’язування.
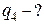 Заряд
Заряд 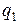 перебуватиме в рівновазі, якщо векторна сума діючих на нього сил дорівнюватиме нулеві:
перебуватиме в рівновазі, якщо векторна сума діючих на нього сил дорівнюватиме нулеві:
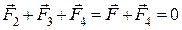 ,
,
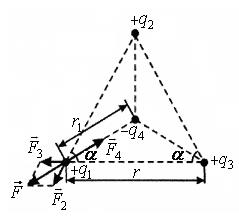
де 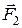 ,
, 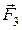 і
і 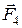 - сили, з якими діють на заряд
- сили, з якими діють на заряд 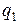 відповідно заряди
відповідно заряди 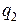 ,
, 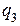 і
і 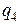 ;
; 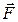 - рівнодійна сил
- рівнодійна сил 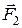 і
і 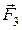 .
.
Оскільки сили 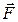 і
і 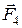 напрямлені по одній прямій, то з (а) випливає, що
напрямлені по одній прямій, то з (а) випливає, що 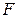 -
- 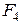 =0, або
=0, або 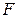 =
= 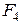 . Виразивши в останньому рівнянні
. Виразивши в останньому рівнянні
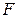 через
через 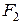 і
і 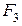 і врахувавши, що
і врахувавши, що 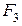 =
= 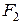 ,
,
Рис.5.2 дістанемо:
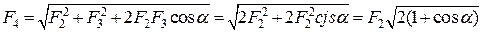 .
.
Згідно із законом Кулона і з урахуванням, що 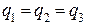 , знайдемо
, знайдемо
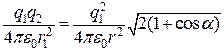 ,
,
звідки
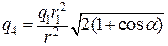 . (б)
. (б)
З геометричних побудов у рівносторонньому трикутнику
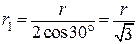 .
.
Підставивши значення 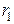 і
і 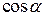 з останніх співвідношень у формулу (б), дістанемо
з останніх співвідношень у формулу (б), дістанемо 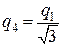 . (в)
. (в)
Підставимо числове значення 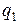 у (в) і знайдемо
у (в) і знайдемо
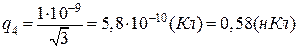 .
.
Відповідь: 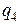 =0,58 нКл.
=0,58 нКл.
5.3. Точковий заряд 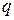 =25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом
=25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом 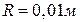 , який рівномірно
, який рівномірно
заряджений і має поверхневу густину заряду 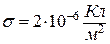 . Визначити силу
. Визначити силу
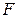 , що діє на заряд, якщо його відстань від осі циліндра
, що діє на заряд, якщо його відстань від осі циліндра 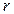 = 0,1м.
= 0,1м.

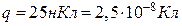 Розв’язування.
Розв’язування.
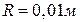 Абсолютне значення сили, що діє на точковий
Абсолютне значення сили, що діє на точковий 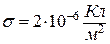 заряд
заряд 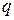 , який знаходиться в електростатичному
, який знаходиться в електростатичному
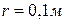 полі, визначають за формулою
полі, визначають за формулою

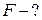
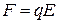 , (а)
, (а)
де 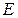 - абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра
- абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра
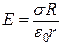 . (б)
. (б)
Підставивши значення Е з (б) у (а), знайдемо робочу формулу
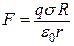 . (в)
. (в)
Підставимо у (в) числові значення фізичних величин і знайдемо значення
сили, що діє на заряд:
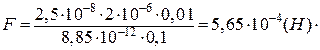
Відповідь: F =5,65 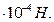
5.4 . Плоский диск радіусом R=0.1м заряджений позитивно. Заряд розподілений по його поверхні зі сталою густиною 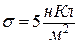 . Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.
. Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.

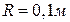 Розв’язування.
Розв’язування.
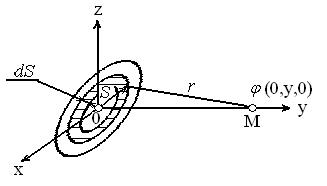
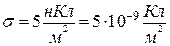 Розмістимо диск так, щоб вісь симетрії збігалася з
Розмістимо диск так, щоб вісь симетрії збігалася з 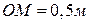 віссю Y прямокутної системи координат (рис.5.3).
віссю Y прямокутної системи координат (рис.5.3).

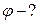 Виділимо на диску вузьке кільце. Якщо через S позначи-
Виділимо на диску вузьке кільце. Якщо через S позначи-
ти радіус цього кільця, а через 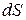 - його ширину, то площа кільця дорівнює
- його ширину, то площа кільця дорівнює 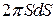 . Кількість електрики, що міститься на ньому, становитиме
. Кількість електрики, що міститься на ньому, становитиме 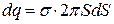 . Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме:
. Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме:
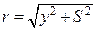 .
.

 Внесок кільцевої поверхн і в потенціал у точці М дорівнює
Внесок кільцевої поверхн і в потенціал у точці М дорівнює
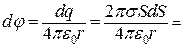
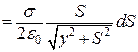 . (а)
. (а)
Рис.5.3 Щоб визначити потенціал,
зумовлений зарядженим диском, слід взяти інтеграл по всіх таких кільцях:
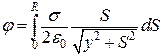 . (б)
. (б)
Зробимо таку підстановку змінних у виразі (б):
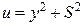 ;
; 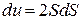 , звідки
, звідки 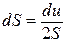 . (в)
. (в)
Замінимо у формулі (б) 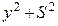 і
і 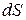 на їхні значения з виразу (в) і дістанемо:
на їхні значения з виразу (в) і дістанемо: 
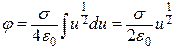
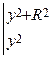
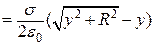 . (г)
. (г)
Підставимо числові значення в формулу (г):
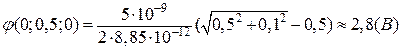 .
.
Відповідь: 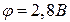 .
.
5.5. У вершинах правильного шестикутника із стороною а поміщають точкові заряди однакової величини 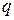 . Знайти потенціал
. Знайти потенціал 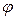 і напруженість Е поля в центрі шестикутника при умові, що:
і напруженість Е поля в центрі шестикутника при умові, що:
1 ) знак усіх зарядів однаковий,
2) знаки сусідніх зарядів протилежні.

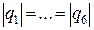 Розв’язування.
Розв’язування.
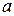 Згідно з принципом суперпозиції полів потенціал поля,
Згідно з принципом суперпозиції полів потенціал поля,

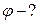 створеного системою зарядів, дорівнює алгебраїчній сумі
створеного системою зарядів, дорівнює алгебраїчній сумі
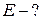 потенціалів, які утворені кожним із зарядів окремо. Врахувавши,
потенціалів, які утворені кожним із зарядів окремо. Врахувавши,
що 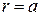 отримаємо:
отримаємо:
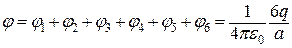 . (а)
. (а)
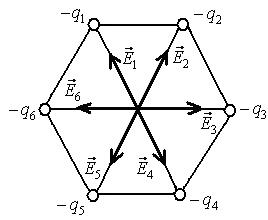
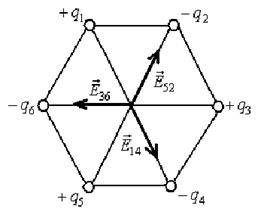
Рис.5.4 Рис.5.5
Напруженість поля системи зарядів дорівнює векторній сумі напруженостей полів, які створював би кожен із зарядів системи самостійно.
Напруженість поля кожного заряду 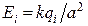 , тобто за величиною всі значення
, тобто за величиною всі значення 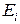 однакові. Внаслідок симетрії системи (рис.5.4):
однакові. Внаслідок симетрії системи (рис.5.4):
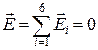 . (б)
. (б)
Міркуючи аналогічним чином, обчислимо потенціал поля у другому випадку:

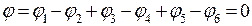 . (в)
. (в)
Напруженість поля 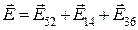 .Із рис.5.5 видно, що
.Із рис.5.5 видно, що 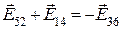 . Отже
. Отже
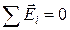 . (г)
. (г)
Відповідь: 1) 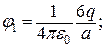
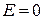
2) 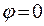 ,
, 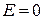 .
.
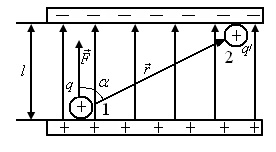
5.6. Знайти роботу 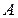 сил електростатичного поля по переміщенню заряду
сил електростатичного поля по переміщенню заряду 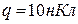 із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань
із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань 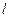 між якими дорівнює
між якими дорівнює 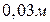 . Поверхнева густина заряду
. Поверхнева густина заряду 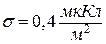 .
.

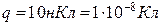 Розв’язування.
Розв’язування.
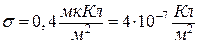 Можливі два способи розв’язування цієї задачі.
Можливі два способи розв’язування цієї задачі.

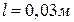 1-й спосіб. Роботу сил поля по переміщенню заряду
1-й спосіб. Роботу сил поля по переміщенню заряду
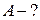 з точки поля з потенціалом
з точки поля з потенціалом 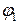 у точку з потенціалом
у точку з потенціалом
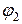 знайдемо за формулою:
знайдемо за формулою:
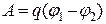 . (а)
. (а)
 Оскільки напруженість поля
Оскільки напруженість поля 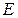 дорівнює градієнту потенціалу з протилежним знаком, то можна записати
дорівнює градієнту потенціалу з протилежним знаком, то можна записати
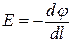 , (б)
, (б)
звідки
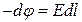 . (в)
. (в)
Проінтегруємо вираз (в), взявши до уваги, Рис.5.6 що поле між нескінченними паралельними
рівномірно різнойменно зарядженими площинами однорідне, його напруженість 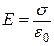 :
:
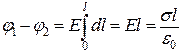 . (г)
. (г)
Підставивши у вираз (а) значення різниці потенціалів із залежності (г), знайдемо
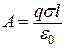 . (д)
. (д)
2-й спосіб. Оскільки поле між площинами однорідне, то сила, що діє на заряд 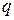 при його переміщенні, стала. Тому роботу сил поля по переміщенню заряду
при його переміщенні, стала. Тому роботу сил поля по переміщенню заряду 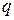 з точки 1 у точку 2 можна знайти за формулою
з точки 1 у точку 2 можна знайти за формулою
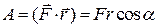 . (е)
. (е)
Врахувавши, що 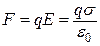 і
і 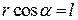 , знайдемо вираз для обчислення роботи:
, знайдемо вираз для обчислення роботи:
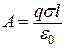 . (є)
. (є)
Отже, обидва способи розв’язування задачі дають один і той самий результат.
Знайдемо числове значення роботи:
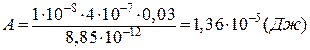 .
.
Відповідь: 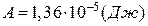 .
.
5.7. Знайти силу 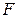 взаємодії двох молекул води, які знаходяться на відстані
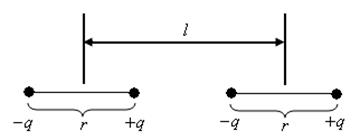
взаємодії двох молекул води, які знаходяться на відстані 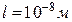 одна від одної (рис.5.7). Електричний дипольний момент молекули води
одна від одної (рис.5.7). Електричний дипольний момент молекули води 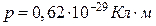 . Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули.
. Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули.
 Розв’язування.
Розв’язування.

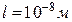
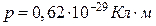
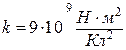

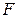 -?
-?
Рис.5.7
Розглянемо випадок, коли диполі лежать на одній прямій і орієнтовані один відносно одного протилежними зарядами, тобто дипольні моменти паралельні. Тоді, згідно з формулою (1.32) та законом Кулона, поле першого диполя діятиме на заряди 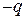 і
і 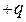 другого диполя відповідно з силами
другого диполя відповідно з силами
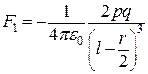 ,
, 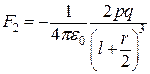 . (а)
. (а)
Оскільки сили 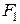 і
і 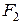 є антипаралельними, то їхня рівнодійна
є антипаралельними, то їхня рівнодійна
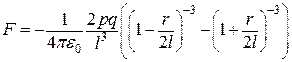 . (б)
. (б)
Враховуючи, що 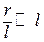 , і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так:
, і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так:
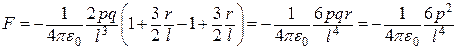 . (в)
. (в)
Виконавши обчислення, отримаємо:
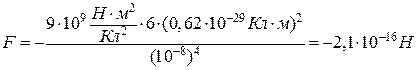 .
.
Знак мінус вказує на те, що диполі притягуються. При антипаралельному розміщенні дипольних моментів значення сили буде таке саме, але додатне, тобто диполі будуть відштовхуватись.
Відповідь: 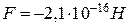 .
.
5.8. Диполь з електричним моментом 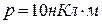 вільно встановився в однорідному електричному полі з напруженістю
вільно встановився в однорідному електричному полі з напруженістю 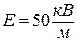 . Визначити зміну потенціальної енергії диполя у разі повороту його на
. Визначити зміну потенціальної енергії диполя у разі повороту його на 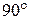 .
.

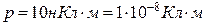 Розв’язування.
Розв’язування.
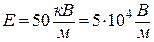 Вивести диполь зі стану стійкої рівноваги
Вивести диполь зі стану стійкої рівноваги
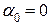 можна лише під дією зовнішніх сил. Тому, по-
можна лише під дією зовнішніх сил. Тому, по-
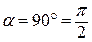 вертаючи диполь на певний кут
вертаючи диполь на певний кут 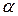 , зовнішні сили
, зовнішні сили
 виконуватимуть додатну роботу, яка витрачати-
виконуватимуть додатну роботу, яка витрачати-
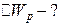 меться на зміну потенціальної енергії диполя:
меться на зміну потенціальної енергії диполя:
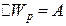 . (а)
. (а)
Елементарна робота 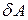 в разі повороту диполя на кут
в разі повороту диполя на кут 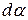 буде
буде
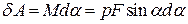 , (б)
, (б)
де 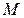 - момент пари сил
- момент пари сил 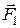 і
і 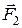 , що діють на заряди диполя з боку електричного поля.
, що діють на заряди диполя з боку електричного поля.
У разі повороту диполя від кута 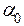 до кута
до кута 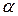 повна робота
повна робота
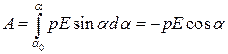
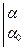 =
= 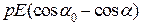 . (в)
. (в)
Величина роботи, виконаної зовнішніми силами, становитиме
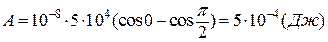 .
.
Згідно з виразом (а) зміна потенціальної енергії диполя
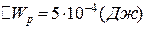 .
.
Відповідь: 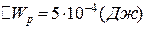 .
.
5.9. Відстані між центрами металевих кульок 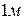 . Радіус кожної з них
. Радіус кожної з них 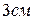 . Кульки відштовхуються з силою
. Кульки відштовхуються з силою 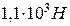 . Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з
. Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з 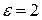 ?
?

 Розв’язування.
Розв’язування.
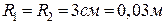 Оскільки кульки мають однакові радіуси і вони
Оскільки кульки мають однакові радіуси і вони 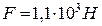 відштовхуються, то очевидно, що заряди кульок
відштовхуються, то очевидно, що заряди кульок

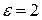 однакові за величиною й однойменні, тобто
однакові за величиною й однойменні, тобто 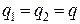 .
.
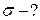 На поверхні кульок заряд розподілений рівномірно з
На поверхні кульок заряд розподілений рівномірно з
поверхневою густиною 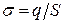 , звідки
, звідки
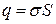 , (а)
, (а)
де 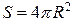 - площа поверхні кульки.
- площа поверхні кульки.
За законом Кулона сила взаємодії зарядів у діелектрику дорівнює
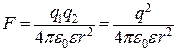 . (б)
. (б)
На підставі формул (а) і (б) отримуємо:
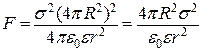 . (в)
. (в)
З рівняння (в) виведемо формулу для визначення 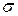 :
:
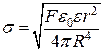 . (г)
. (г)
Знайдемо числове значення поверхневої густини електричних зарядів кульок
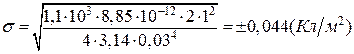 .
.
Відповідь: 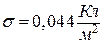 , якщо заряди кульок позитивні;
, якщо заряди кульок позитивні; 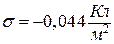 , якщо заряди кульок негативні.
, якщо заряди кульок негативні.
5.10. Конденсатори 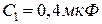 ,
, 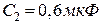 ,
, 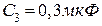 ,
, 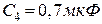 з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками
з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками 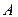 і
і 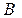 дорівнює
дорівнює 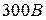 . Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.
. Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.
Розв’язування.

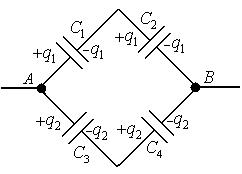
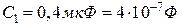 Як видно з рисунка,
Як видно з рисунка,
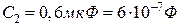 конденсатори
конденсатори 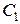 і
і 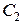
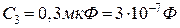 та
та 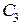 і
і 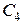 відповідно
відповідно
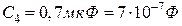 з’єднані послідовно в
з’єднані послідовно в
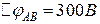 дві ланки, а ці ланки
дві ланки, а ці ланки
 з’єднані паралельно
з’єднані паралельно
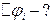 в точках
в точках 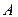 і
і 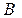 .
.
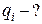 У разі послідовного
У разі послідовного
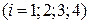 Рис.5.8 з’єднання конденса-
Рис.5.8 з’єднання конденса-
торів заряд на всіх обкладках за абсолютною величиною буде однаковим.
Позначимо ці заряди на обкладках конденсаторів першої ланки 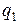 , а другої -
, а другої - 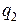 . Різниця потенціалів на першому конденсаторі
. Різниця потенціалів на першому конденсаторі 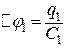 , на дру-
, на дру-
гому - 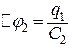 , на третьому -
, на третьому - 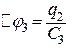 , на четвертому -
, на четвертому - 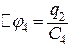 . Причому
. Причому
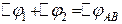 і
і 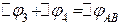 . Визначимо заряд
. Визначимо заряд 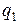 :
:
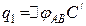 , (а)
, (а)
де 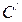 - електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її:
- електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її:
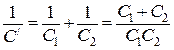 ,
,
звідки
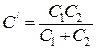 . (б)
. (б)
Підставимо 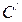 із (б) у вираз (а) й отримаємо:
із (б) у вираз (а) й отримаємо:
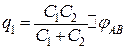 . (в)
. (в)
Аналогічно знайдемо, що
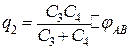 . (г)
. (г)
Тоді
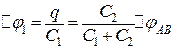 ;
; 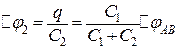 ;
;
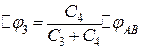 ;
; 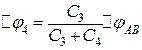 .
.
Обчислимо їх значення:
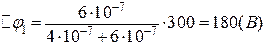 ;
; 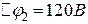 ;
; 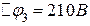 ;
; 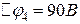 .
.
Заряди на пластинках конденсатора можна знаходити або за формулами (в) і (г), або за формулами різниці потенціалів між обкладками на одному з конденсаторів, взятому з першої та другої ланок. Так,
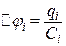 ,
,
звідки
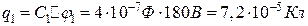 ;
;
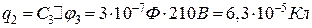 .
.
Відповідь: 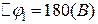 ;
; 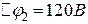 ;
; 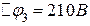 ;
; 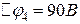 ;
; 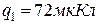 ;
; 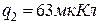 .
.
5.11. Відстань між обкладками плоского конденсатора 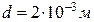 , різниця потенціалів
, різниця потенціалів 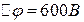 . Заряд кожної обкладки
. Заряд кожної обкладки 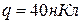 . Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.
. Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.

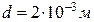 Розв’язування.
Розв’язування.
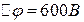 Енергія електричного поля плоского конденсатора:
Енергія електричного поля плоского конденсатора:
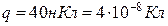
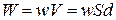 , (а)
, (а)

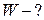 де
де 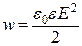 -об’ємна густина енергії електричного
-об’ємна густина енергії електричного
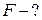 поля,
поля, 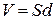 - об’єм конденсатора. Підставимо у
- об’єм конденсатора. Підставимо у
формулу (а) вираз для визначення 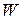 :
:
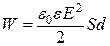 . (б)
. (б)
Електричне поле плоского конденсатора однорідне, тому його напруженість 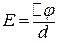 . Підставимо цей вираз у (б) і зробимо перетворення:
. Підставимо цей вираз у (б) і зробимо перетворення:
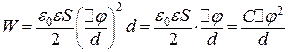 . (в)
. (в)
Оскільки відомий заряд на обкладках, то електроємність знайдемо через заряд і різницю потенціалів 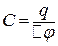 . Підставимо цей вираз С у формулу (в):
. Підставимо цей вираз С у формулу (в):
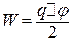 . (г)
. (г)
Обчислимо
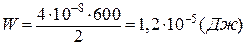 .
.
Для того, щоб розвести обкладки конденсатора на відстань 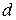 , необхідно виконати роботу проти сил протягування
, необхідно виконати роботу проти сил протягування 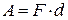 . Ця робота витрачається на зміни енергії конденсатора:
. Ця робота витрачається на зміни енергії конденсатора: 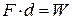 . Отже
. Отже
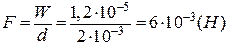 .
.
Відповідь: 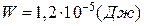 ;
; 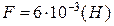 .
.
5.12. Електричне поле створено провідною зарядженою ( 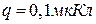 ) кулею радіусом
) кулею радіусом 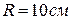 . Яка енергія
. Яка енергія 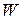 поля зосереджена в об’ємі, обмеженому кулею і концентричною з нею сферичною поверхнею, радіус якої вдвічі більший радіуса кулі?
поля зосереджена в об’ємі, обмеженому кулею і концентричною з нею сферичною поверхнею, радіус якої вдвічі більший радіуса кулі?

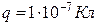 Розв’язування.
Розв’язування.
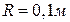 Оскільки куля провідна, то заряд
Оскільки куля провідна, то заряд 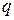 розподілиться по її
розподілиться по її
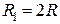 поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її
поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її

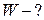 межами заряд кулі можна вважати точковим. Напруженість
межами заряд кулі можна вважати точковим. Напруженість
поля, створеного зарядом 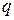 в точці на відстані
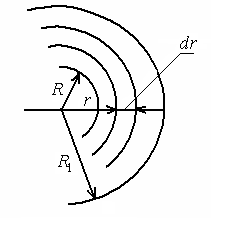
в точці на відстані 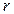 від центра кулі (рис.5.9)
від центра кулі (рис.5.9)
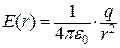 .
.
Енергія електричного поля у заданому об’ємі дорівнює:
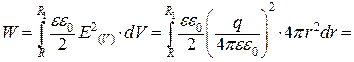
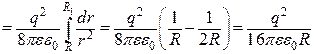 (а)
(а)
Враховуючи задані величини, на підставі формули (а) отримуємо:
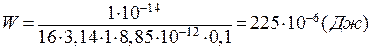 .
.
Відповідь: 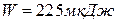 .
.
Рис.5.9





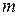 , підвішені в одній точці на умовно нерозтяжних нитках довжиною
, підвішені в одній точці на умовно нерозтяжних нитках довжиною 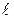 . Відстань між кульками
. Відстань між кульками 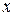 <<
<<  з кожної кульки, якщо швидкість їх зближення змінюється за законом
з кожної кульки, якщо швидкість їх зближення змінюється за законом 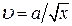 , де
, де 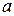 -стала.
-стала.

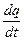 -? через точку підвісу, то доцільно розглянути сили, які діють на одну
-? через точку підвісу, то доцільно розглянути сили, які діють на одну
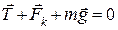 . (а)
. (а)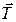 - реакція нитки,
- реакція нитки, 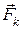 - кулонівська сила взаємодії між кульками,
- кулонівська сила взаємодії між кульками, 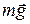 - сила тяжіння. Запишемо рівняння (а) у проекціях на координатні осі x та y:
- сила тяжіння. Запишемо рівняння (а) у проекціях на координатні осі x та y: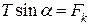 ;
; 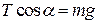 . (б)
. (б)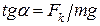 . (в)
. (в)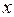 <<
<< 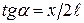 . Враховуючи закон Кулона, на підставі
. Враховуючи закон Кулона, на підставі 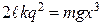 . (г)
. (г)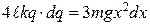 .
.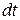 зближення кульок
зближення кульок 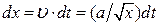 і враховуючи, що згідно з рівнянням (г)
і враховуючи, що згідно з рівнянням (г)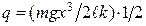 і що
і що 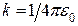 , знаходимо кінцеве рівняння у загальному вигляді:
, знаходимо кінцеве рівняння у загальному вигляді: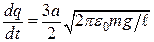 .
.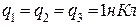 розміщені у вершинах рівностороннього трикутника (рис.5.2). Який негативний точковий заряд
розміщені у вершинах рівностороннього трикутника (рис.5.2). Який негативний точковий заряд 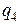 потрібно помістити в центр трикутника, щоб сила притягання з його боку зрівноважила сили взаємного відштовхування зарядів, які знаходяться у вершинах?
потрібно помістити в центр трикутника, щоб сила притягання з його боку зрівноважила сили взаємного відштовхування зарядів, які знаходяться у вершинах?

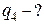 Заряд
Заряд 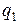 перебуватиме в рівновазі, якщо векторна сума діючих на нього сил дорівнюватиме нулеві:
перебуватиме в рівновазі, якщо векторна сума діючих на нього сил дорівнюватиме нулеві: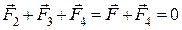 ,
, 
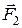 ,
, 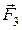 і
і 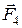 - сили, з якими діють на заряд
- сили, з якими діють на заряд 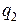 ,
, 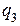 і
і 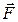 - рівнодійна сил
- рівнодійна сил 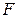 -
- 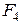 =0, або
=0, або 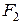 і
і 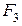 і врахувавши, що
і врахувавши, що 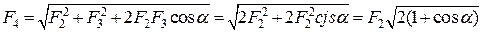 .
.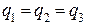 , знайдемо
, знайдемо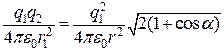 ,
,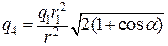 . (б)
. (б)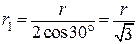 .
.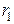 і
і 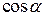 з останніх співвідношень у формулу (б), дістанемо
з останніх співвідношень у формулу (б), дістанемо 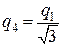 . (в)
. (в)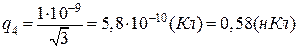 .
.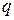 =25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом
=25нКл знаходиться в електростатичному полі нескінченно довгого циліндра радіусом 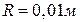 , який рівномірно
, який рівномірно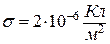 . Визначити силу
. Визначити силу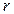 = 0,1м.
= 0,1м.
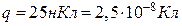 Розв’язування.
Розв’язування.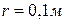 полі, визначають за формулою
полі, визначають за формулою
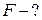
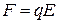 , (а)
, (а) 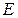 - абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра
- абсолютне значення напруженості електростатичного поля. Напруженість поля нескінченно довгого рівномірно зарядженого циліндра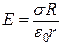 . (б)
. (б)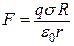 . (в)
. (в)
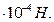
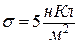 . Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.
. Визначити потенціал електростатичного поля в точці М на осі симетрії, віддаленій від центра диска на 0,5м.
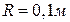 Розв’язування.
Розв’язування.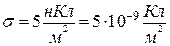 Розмістимо диск так, щоб вісь симетрії збігалася з
Розмістимо диск так, щоб вісь симетрії збігалася з 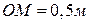 віссю Y прямокутної системи координат (рис.5.3).
віссю Y прямокутної системи координат (рис.5.3).
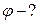 Виділимо на диску вузьке кільце. Якщо через S позначи-
Виділимо на диску вузьке кільце. Якщо через S позначи-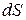 - його ширину, то площа кільця дорівнює
- його ширину, то площа кільця дорівнює 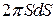 . Кількість електрики, що міститься на ньому, становитиме
. Кількість електрики, що міститься на ньому, становитиме 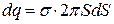 . Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме:
. Усі елементи заряду на вузькому кільці диска розміщені на однаковій відстані від точки М, а саме: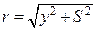 .
.
 Внесок кільцевої поверхн і в потенціал у точці М дорівнює
Внесок кільцевої поверхн і в потенціал у точці М дорівнює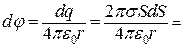
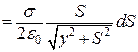 . (а)
. (а) 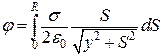 . (б)
. (б)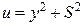 ;
; 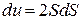 , звідки
, звідки 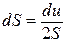 . (в)
. (в)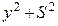 і
і 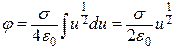
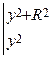
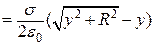 . (г)
. (г)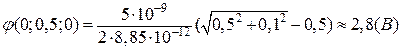 .
.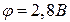 .
.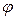 і напруженість Е поля в центрі шестикутника при умові, що:
і напруженість Е поля в центрі шестикутника при умові, що:
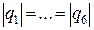 Розв’язування.
Розв’язування.
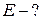 потенціалів, які утворені кожним із зарядів окремо. Врахувавши,
потенціалів, які утворені кожним із зарядів окремо. Врахувавши,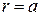 отримаємо:
отримаємо: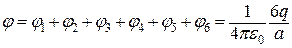 . (а)
. (а) 

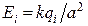 , тобто за величиною всі значення
, тобто за величиною всі значення 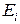 однакові. Внаслідок симетрії системи (рис.5.4):
однакові. Внаслідок симетрії системи (рис.5.4):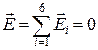 . (б)
. (б)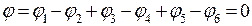 . (в)
. (в)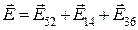 .Із рис.5.5 видно, що
.Із рис.5.5 видно, що 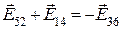 . Отже
. Отже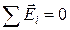 . (г)
. (г)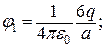
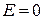
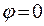 ,
, 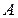 сил електростатичного поля по переміщенню заряду
сил електростатичного поля по переміщенню заряду 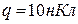 із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань
із точки 1 в точку 2 (рис.5.6), що знаходяться між двома різноймен- но зарядженими площинами, відстань 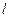 між якими дорівнює
між якими дорівнює 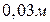 . Поверхнева густина заряду
. Поверхнева густина заряду 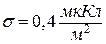 .
.
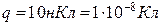 Розв’язування.
Розв’язування.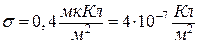 Можливі два способи розв’язування цієї задачі.
Можливі два способи розв’язування цієї задачі.
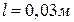 1-й спосіб. Роботу сил поля по переміщенню заряду
1-й спосіб. Роботу сил поля по переміщенню заряду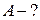 з точки поля з потенціалом
з точки поля з потенціалом 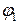 у точку з потенціалом
у точку з потенціалом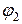 знайдемо за формулою:
знайдемо за формулою: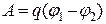 . (а)
. (а) Оскільки напруженість поля
Оскільки напруженість поля 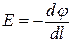 , (б)
, (б) 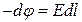 . (в)
. (в) 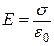 :
: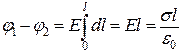 . (г)
. (г)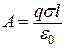 . (д)
. (д)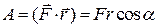 . (е)
. (е)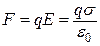 і
і 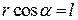 , знайдемо вираз для обчислення роботи:
, знайдемо вираз для обчислення роботи: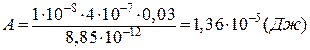 .
.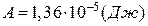 .
.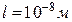 одна від одної (рис.5.7). Електричний дипольний момент молекули води
одна від одної (рис.5.7). Електричний дипольний момент молекули води 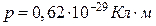 . Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули.
. Дипольні моменти молекул вважати розміщеними вздовж прямої, що з’єднує молекули. Розв’язування.
Розв’язування.
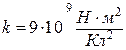

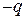 і
і 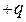 другого диполя відповідно з силами
другого диполя відповідно з силами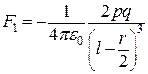 ,
, 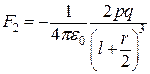 . (а)
. (а)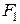 і
і 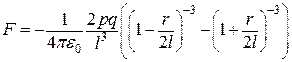 . (б)
. (б)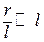 , і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так:
, і нехтуючи величинами вищих порядків малості, вираз (б) можна записати так: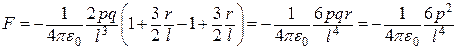 . (в)
. (в)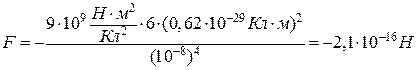 .
.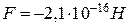 .
.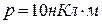 вільно встановився в однорідному електричному полі з напруженістю
вільно встановився в однорідному електричному полі з напруженістю 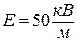 . Визначити зміну потенціальної енергії диполя у разі повороту його на
. Визначити зміну потенціальної енергії диполя у разі повороту його на 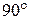 .
.
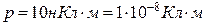 Розв’язування.
Розв’язування.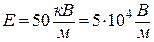 Вивести диполь зі стану стійкої рівноваги
Вивести диполь зі стану стійкої рівноваги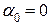 можна лише під дією зовнішніх сил. Тому, по-
можна лише під дією зовнішніх сил. Тому, по-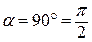 вертаючи диполь на певний кут
вертаючи диполь на певний кут 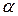 , зовнішні сили
, зовнішні сили виконуватимуть додатну роботу, яка витрачати-
виконуватимуть додатну роботу, яка витрачати-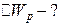 меться на зміну потенціальної енергії диполя:
меться на зміну потенціальної енергії диполя: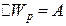 . (а)
. (а)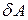 в разі повороту диполя на кут
в разі повороту диполя на кут 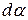 буде
буде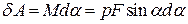 , (б)
, (б) 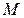 - момент пари сил
- момент пари сил 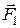 і
і 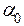 до кута
до кута 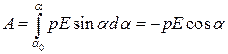
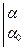 =
= 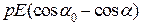 . (в)
. (в) 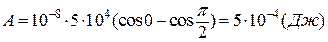 .
.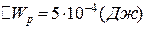 .
.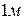 . Радіус кожної з них
. Радіус кожної з них 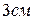 . Кульки відштовхуються з силою
. Кульки відштовхуються з силою 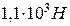 . Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з
. Чому дорівнює поверхнева густина електричних зарядів кульок, якщо вони знаходяться в діелектрику з 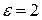 ?
?
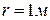 Розв’язування.
Розв’язування.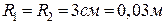 Оскільки кульки мають однакові радіуси і вони
Оскільки кульки мають однакові радіуси і вони 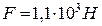 відштовхуються, то очевидно, що заряди кульок
відштовхуються, то очевидно, що заряди кульок
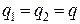 .
.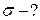 На поверхні кульок заряд розподілений рівномірно з
На поверхні кульок заряд розподілений рівномірно з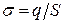 , звідки
, звідки 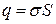 , (а)
, (а)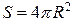 - площа поверхні кульки.
- площа поверхні кульки.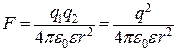 . (б)
. (б)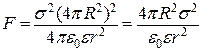 . (в)
. (в)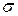 :
: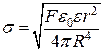 . (г)
. (г)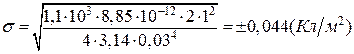 .
.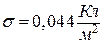 , якщо заряди кульок позитивні;
, якщо заряди кульок позитивні; 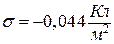 , якщо заряди кульок негативні.
, якщо заряди кульок негативні.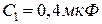 ,
, 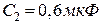 ,
, 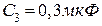 ,
, 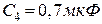 з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками
з’єднані так, як показано на рис.5.8. Різниця потенціалів між точками 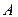 і
і 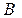 дорівнює
дорівнює 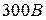 . Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.
. Обчислити різницю потенціалів на кожному з конденсаторів і заряд на його обкладках.

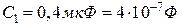 Як видно з рисунка,
Як видно з рисунка, 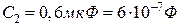 конденсатори
конденсатори 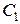 і
і 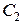
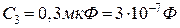 та
та 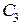 і
і 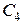 відповідно
відповідно 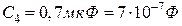 з’єднані послідовно в
з’єднані послідовно в 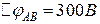 дві ланки, а ці ланки
дві ланки, а ці ланки з’єднані паралельно
з’єднані паралельно 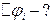 в точках
в точках 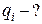 У разі послідовного
У разі послідовного 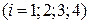 Рис.5.8 з’єднання конденса-
Рис.5.8 з’єднання конденса- 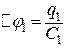 , на дру-
, на дру-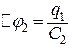 , на третьому -
, на третьому - 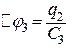 , на четвертому -
, на четвертому - 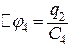 . Причому
. Причому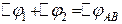 і
і 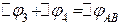 . Визначимо заряд
. Визначимо заряд 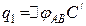 , (а)
, (а)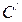 - електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її:
- електроємність першої ланки конденсаторів, сполучених послідовно. Знайдемо її: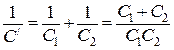 ,
,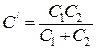 . (б)
. (б)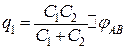 . (в)
. (в)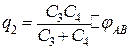 . (г)
. (г)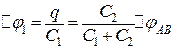 ;
; 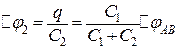 ;
;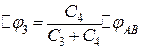 ;
; 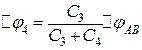 .
.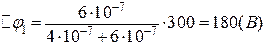 ;
; 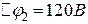 ;
; 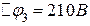 ;
; 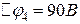 .
.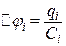 ,
,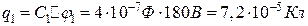 ;
;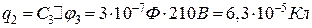 .
.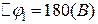 ;
; 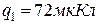 ;
; 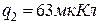 .
.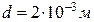 , різниця потенціалів
, різниця потенціалів 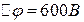 . Заряд кожної обкладки
. Заряд кожної обкладки 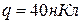 . Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.
. Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.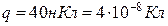
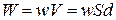 , (а)
, (а)
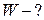 де
де 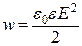 -об’ємна густина енергії електричного
-об’ємна густина енергії електричного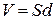 - об’єм конденсатора. Підставимо у
- об’єм конденсатора. Підставимо у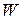 :
: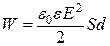 . (б)
. (б)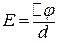 . Підставимо цей вираз у (б) і зробимо перетворення:
. Підставимо цей вираз у (б) і зробимо перетворення: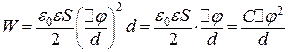 . (в)
. (в)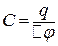 . Підставимо цей вираз С у формулу (в):
. Підставимо цей вираз С у формулу (в):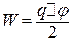 . (г)
. (г)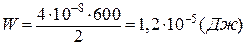 .
.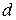 , необхідно виконати роботу проти сил протягування
, необхідно виконати роботу проти сил протягування 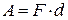 . Ця робота витрачається на зміни енергії конденсатора:
. Ця робота витрачається на зміни енергії конденсатора: 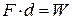 . Отже
. Отже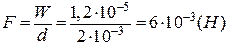 .
.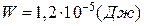 ;
; 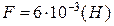 .
.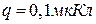 ) кулею радіусом
) кулею радіусом 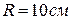 . Яка енергія
. Яка енергія 
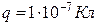 Розв’язування.
Розв’язування.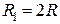 поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її
поверхні і в об’ємі кулі поле відсутнє. На поверхні кулі і за її 
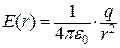 .
.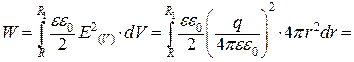
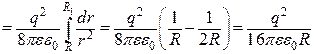 (а)
(а)
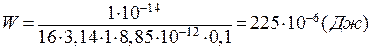 .
.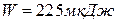 .
.


