Теорема Гаусcа дає можливість досить часто розрахувати напруженість більш простим засобом, аніж на підставі формули (1.11). Розглянемо кілька прикладів.
Електричне поле рівномірно зарядженої нескінченної площини
Площину можна вважати нескінченною, якщо відстань від точки, в якій визначається напруженість поля до площини, дуже мала порівняно з геометричними розмірами площини. Обчислимо напруженість електростатичного поля, створюваного такою площиною з поверхневою густиною заряду 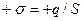 , де + q – заряд, наданий площині загальною площею S.
, де + q – заряд, наданий площині загальною площею S.
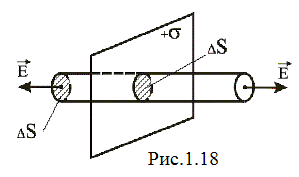 Внаслідок симетрії поля лінії напруженості напрямлені перпендикулярно до площини. В якості замкненої поверхні зручно (і найпростіше) обрати поверхню циліндра, твірні якого перпендикулярні до площини (рис. 1.18).
Внаслідок симетрії поля лінії напруженості напрямлені перпендикулярно до площини. В якості замкненої поверхні зручно (і найпростіше) обрати поверхню циліндра, твірні якого перпендикулярні до площини (рис. 1.18).
Згідно з теоремою Гаусcа (1.44) знаходимо: 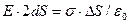 , звідки
, звідки 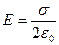 . Отже, отриманий результат не залежить від довжини циліндра, тобто
. Отже, отриманий результат не залежить від довжини циліндра, тобто  не залежить від відстані до нескінченної рівномірно зарядженої площини. На далекій відстані від площини її заряд розглядається як точковий.
не залежить від відстані до нескінченної рівномірно зарядженої площини. На далекій відстані від площини її заряд розглядається як точковий.
Електричне поле двох паралельних різнойменно заряджених площин
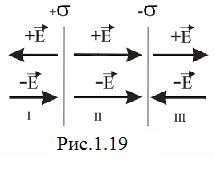 Нехай дві паралельні, рівномірно заряджені площини мають поверхневі густини зарядів +s та - s (рис. 1.19). Тоді очевидно, що в кожній області простору (I , II та III) напруженість поля
Нехай дві паралельні, рівномірно заряджені площини мають поверхневі густини зарядів +s та - s (рис. 1.19). Тоді очевидно, що в кожній області простору (I , II та III) напруженість поля 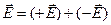 . В областях I та III за величиною
. В областях I та III за величиною 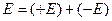 , а в області II
, а в області II 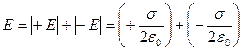 , якщо
, якщо 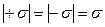 , то в областях I та III
, то в областях I та III 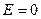 , а в області II
, а в області II 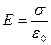 . У всіх областях поле однорідне, за винятком країв площин.
. У всіх областях поле однорідне, за винятком країв площин.
Поле нескінченної рівномірно зарядженої циліндричної поверхні
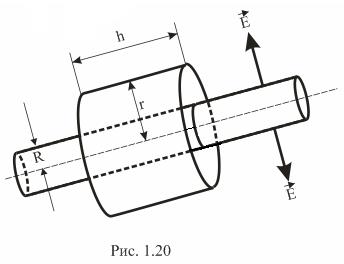 Нехай нескінченно довга циліндрична поверхня радіуса R має незмінну поверхневу густину заряду + s. Внаслідок симетрії електростатичного поля лінії вектора
Нехай нескінченно довга циліндрична поверхня радіуса R має незмінну поверхневу густину заряду + s. Внаслідок симетрії електростатичного поля лінії вектора 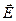 в якій завгодно точці циліндра, за винятком його основ, спрямовані уздовж радіальної прямої, перпендикулярної до осі циліндра (рис. 1.20). У такому випадку
в якій завгодно точці циліндра, за винятком його основ, спрямовані уздовж радіальної прямої, перпендикулярної до осі циліндра (рис. 1.20). У такому випадку 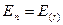 . Для обчислення напруженості поля в довільно обраній точці на відстані r в якості замкненої поверхні оберемо поверхню циліндра радіуса r і висотою h, коаксіального зарядженому циліндру. Потік вектора
. Для обчислення напруженості поля в довільно обраній точці на відстані r в якості замкненої поверхні оберемо поверхню циліндра радіуса r і висотою h, коаксіального зарядженому циліндру. Потік вектора 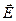 через площі основ цього циліндра дорівнює нулеві. Якщо r < R, то всередині такого циліндра заряду немає і поле відсутнє. Отже, згідно з теоремою Гауса отримаємо:
через площі основ цього циліндра дорівнює нулеві. Якщо r < R, то всередині такого циліндра заряду немає і поле відсутнє. Отже, згідно з теоремою Гауса отримаємо:
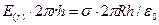 , звідки
, звідки 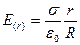 .
.
Величина  являє собою лінійну густину заряду (заряд, що приходиться на одиницю довжини зарядженого циліндра). Тоді напруженість поля на відстані r від циліндра
являє собою лінійну густину заряду (заряд, що приходиться на одиницю довжини зарядженого циліндра). Тоді напруженість поля на відстані r від циліндра 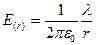 . Отриманий результат виконується для точок на відстанях r, набагато менших від довжини циліндра і не виконуються на його кінцях.
. Отриманий результат виконується для точок на відстанях r, набагато менших від довжини циліндра і не виконуються на його кінцях.





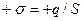 , де + q – заряд, наданий площині загальною площею S.
, де + q – заряд, наданий площині загальною площею S. Внаслідок симетрії поля лінії напруженості напрямлені перпендикулярно до площини. В якості замкненої поверхні зручно (і найпростіше) обрати поверхню циліндра, твірні якого перпендикулярні до площини (рис. 1.18).
Внаслідок симетрії поля лінії напруженості напрямлені перпендикулярно до площини. В якості замкненої поверхні зручно (і найпростіше) обрати поверхню циліндра, твірні якого перпендикулярні до площини (рис. 1.18).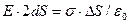 , звідки
, звідки 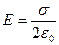 . Отже, отриманий результат не залежить від довжини циліндра, тобто
. Отже, отриманий результат не залежить від довжини циліндра, тобто 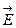 не залежить від відстані до нескінченної рівномірно зарядженої площини. На далекій відстані від площини її заряд розглядається як точковий.
не залежить від відстані до нескінченної рівномірно зарядженої площини. На далекій відстані від площини її заряд розглядається як точковий. Нехай дві паралельні, рівномірно заряджені площини мають поверхневі густини зарядів +s та - s (рис. 1.19). Тоді очевидно, що в кожній області простору (I , II та III) напруженість поля
Нехай дві паралельні, рівномірно заряджені площини мають поверхневі густини зарядів +s та - s (рис. 1.19). Тоді очевидно, що в кожній області простору (I , II та III) напруженість поля 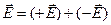 . В областях I та III за величиною
. В областях I та III за величиною 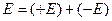 , а в області II
, а в області II 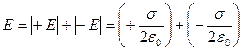 , якщо
, якщо 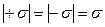 , то в областях I та III
, то в областях I та III 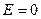 , а в області II
, а в області II 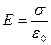 . У всіх областях поле однорідне, за винятком країв площин.
. У всіх областях поле однорідне, за винятком країв площин. Нехай нескінченно довга циліндрична поверхня радіуса R має незмінну поверхневу густину заряду + s. Внаслідок симетрії електростатичного поля лінії вектора
Нехай нескінченно довга циліндрична поверхня радіуса R має незмінну поверхневу густину заряду + s. Внаслідок симетрії електростатичного поля лінії вектора 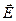 в якій завгодно точці циліндра, за винятком його основ, спрямовані уздовж радіальної прямої, перпендикулярної до осі циліндра (рис. 1.20). У такому випадку
в якій завгодно точці циліндра, за винятком його основ, спрямовані уздовж радіальної прямої, перпендикулярної до осі циліндра (рис. 1.20). У такому випадку 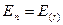 . Для обчислення напруженості поля в довільно обраній точці на відстані r в якості замкненої поверхні оберемо поверхню циліндра радіуса r і висотою h, коаксіального зарядженому циліндру. Потік вектора
. Для обчислення напруженості поля в довільно обраній точці на відстані r в якості замкненої поверхні оберемо поверхню циліндра радіуса r і висотою h, коаксіального зарядженому циліндру. Потік вектора 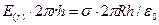 , звідки
, звідки 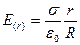 .
. являє собою лінійну густину заряду (заряд, що приходиться на одиницю довжини зарядженого циліндра). Тоді напруженість поля на відстані r від циліндра
являє собою лінійну густину заряду (заряд, що приходиться на одиницю довжини зарядженого циліндра). Тоді напруженість поля на відстані r від циліндра 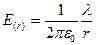 . Отриманий результат виконується для точок на відстанях r, набагато менших від довжини циліндра і не виконуються на його кінцях.
. Отриманий результат виконується для точок на відстанях r, набагато менших від довжини циліндра і не виконуються на його кінцях.


