Знаючи дивергенцію будь-якого вектора в кожній точці простору, можна обчислити потік цього вектора через яку завгодно замкнену поверхню обмежених розмірів. Знайдемо його на прикладі рідини з заданим полем швидкості 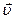 . Добуток
. Добуток 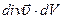 дає потужність в об’ємі
дає потужність в об’ємі 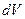 . Сума таких добутків, тобто
. Сума таких добутків, тобто 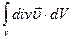 дає потужність джерел в об’ємі
дає потужність джерел в об’ємі 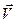 . Таким чином отримуємо співвідношення:
. Таким чином отримуємо співвідношення:
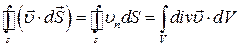 .
.
Для будь-якого вектора 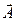 маємо:
маємо:
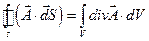 . (1.49)
. (1.49)
Співвідношення (1.49) називають теоремою Остроградського–Гаусса.
Для електростатичного поля вона набирає вигляду:
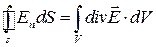 . (1.50)
. (1.50)
На підставі формул (1.42), (1.48) та (1.50) отримуємо:
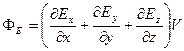 .
.
1.9.5. Циркуляція вектора 
Повернемося знову до течії ідеальної рідини, що не стискається. Уявімо собі замкнену лінію – контур  . Припустимо, що якимось чином ми миттєво ззаморозимо рідину у всьому об’ємі, за винятком дуже тонкого замкненого каналу постійного перетину
. Припустимо, що якимось чином ми миттєво ззаморозимо рідину у всьому об’ємі, за винятком дуже тонкого замкненого каналу постійного перетину 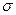 , який вміщує в себе контур
, який вміщує в себе контур 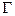 (рис. 1.16). В залежності від характеру поля вектора швидкості
(рис. 1.16). В залежності від характеру поля вектора швидкості 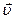 рідина в каналі може бу-
рідина в каналі може бу-
ти або нерухомою, або буде 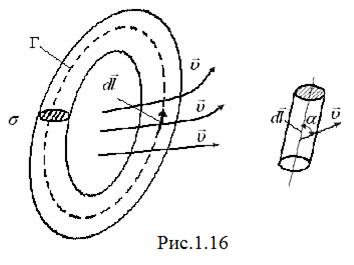 ру-
ру-
хатися уздовж контуру (циркулювати) в одному із двох можливих напрямів.
Оскільки рідина ідеальна, то дія стінок каналу може змінити лише напрям імпульсу молекули, а взаємодія між молекулами призведе до вирівнювання швидкості між ними. Імпульс частинок рідини в об’ємі каналу, що відповідає його ділянці 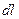 , за величиною буде дорівнювати
, за величиною буде дорівнювати 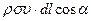 , де
, де 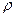 – густина рідини,
– густина рідини, 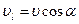 – проекція швидкості
– проекція швидкості 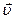 на напрям
на напрям 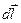 . Імпульс рідини у всьому каналі буде дорівнювати
. Імпульс рідини у всьому каналі буде дорівнювати
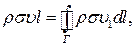 ,
,
де 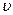 – швидкість циркуляції. Скоротивши попередній вираз на
– швидкість циркуляції. Скоротивши попередній вираз на 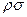 , отримаємо, що циркуляція
, отримаємо, що циркуляція 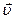 по
по 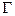 дорівнює
дорівнює 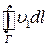 .
.
Для будь-якого вектора 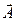 циркуляція по довільному контуру
циркуляція по довільному контуру 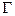 :
: 

циркуляція 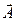 по
по 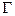 дорівнює
дорівнює 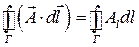 (1.51)
(1.51)
Аналогічно визначається циркуляція вектора напруженості 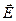 електричного поля по довільному контуру
електричного поля по довільному контуру 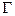 :
:
циркуляція 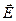 по
по 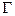 дорівнює
дорівнює 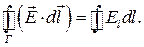 (1.52)
(1.52)
У §1.4 було доведено, що для електростатичного поля 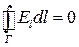 . Отже, векторне поле напруженістю
. Отже, векторне поле напруженістю 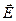 є потенціальним, якщо циркуляція вектора
є потенціальним, якщо циркуляція вектора 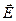 по довільному замкненому контуру дорівнює нулеві.
по довільному замкненому контуру дорівнює нулеві.
1 .9.6. Ротор вектора 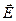
Циркуляція вектора 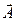 характеризує властивості векторного поля, усереднені по поверхні, що охоплюється контуром
характеризує властивості векторного поля, усереднені по поверхні, що охоплюється контуром 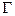 . Щоб отримати характеристику поля в точці
. Щоб отримати характеристику поля в точці 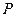 цієї поверхні, необхідно зменшувати розміри контуру, стягуючи його в точку
цієї поверхні, необхідно зменшувати розміри контуру, стягуючи його в точку 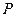 . При цьому необмежено зменшується як циркуляція, так і площа
. При цьому необмежено зменшується як циркуляція, так і площа 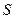 , що охоплюється контуром. Відношення циркуляції до площі
, що охоплюється контуром. Відношення циркуляції до площі 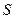 прагне до деякої границі, яку і використовують в якості характеристики поля в точці
прагне до деякої границі, яку і використовують в якості характеристики поля в точці 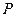 .
.
Візьмемо контур 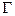 , що лежить в площині, в якій знаходиться точка
, що лежить в площині, в якій знаходиться точка 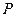 , і розглянемо вираз:
, і розглянемо вираз:
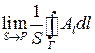 , (1.53)
, (1.53)
де 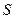 - площа, що охоплюється контуром. Обчислена для довільно взятої площини границя (1.53) не може бути характеристикою поля в точці
- площа, що охоплюється контуром. Обчислена для довільно взятої площини границя (1.53) не може бути характеристикою поля в точці  , оскільки величина цієї границі залежить не лише від властивостей поля в точці
, оскільки величина цієї границі залежить не лише від властивостей поля в точці  , але і від орієнтації контуру в просторі. Ця орієнтація може бути задана напрямом позитивної нормалі
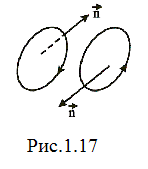
, але і від орієнтації контуру в просторі. Ця орієнтація може бути задана напрямом позитивної нормалі 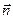 до площини контуру (позитивною вважається нормаль, зв’язана з напрямом обходу по контуру при інтегруванні правилом правого гвинта (рис.1.17). Границя (1.53) в одній і тій самій точці
до площини контуру (позитивною вважається нормаль, зв’язана з напрямом обходу по контуру при інтегруванні правилом правого гвинта (рис.1.17). Границя (1.53) в одній і тій самій точці 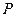 для різних напрямів матиме різні значення, які для протилежних напрямів відрізняються лише знаком. Для якогось певного напряму нормалі
для різних напрямів матиме різні значення, які для протилежних напрямів відрізняються лише знаком. Для якогось певного напряму нормалі 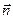 величина (1.53) в вибраній точці буде максимальною.
величина (1.53) в вибраній точці буде максимальною.
Оскільки циркуляція – це величина скалярна, а характеристика поля в точці 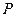 залежить від напряму обходу по контуру, то очевидно, що величина (1.53) поводить себе як проекція деякого вектора на напрям нормалі до площини контуру, по якому береться циркуляція. Максимальне значення величини (1.53) визначає модуль цього вектора, а напрям позитивної нормалі
залежить від напряму обходу по контуру, то очевидно, що величина (1.53) поводить себе як проекція деякого вектора на напрям нормалі до площини контуру, по якому береться циркуляція. Максимальне значення величини (1.53) визначає модуль цього вектора, а напрям позитивної нормалі 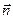 , при якому досягається максимум, вказує напрям вектора. Цей вектор називають ротором (або вихорем) вектора
, при якому досягається максимум, вказує напрям вектора. Цей вектор називають ротором (або вихорем) вектора 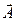 . Позначають його символом
. Позначають його символом 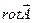 . Скориставшись цим символом, вираз (1.53) можна записати у вигляді
. Скориставшись цим символом, вираз (1.53) можна записати у вигляді
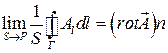 , (1.54)
, (1.54)
де 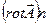 – проекція вектора
– проекція вектора 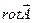 на позитивну нормаль до площини
на позитивну нормаль до площини 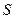 , що обмежується контуром
, що обмежується контуром 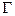 .
.
Вираз (1.54) визначає вектор 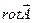 . Це визначення є самим загальним і не залежить від вигляду координатної системи.
. Це визначення є самим загальним і не залежить від вигляду координатної системи.
По аналогії з (1.54) для вектора напруженості електричного поля отримаємо:
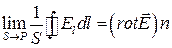 , (1.55)
, (1.55)
де 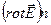 – має такий самий зміст, як і
– має такий самий зміст, як і 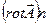 .
.
Проекції вектора 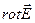 на координатні осі декартової системи мають вигляд:
на координатні осі декартової системи мають вигляд:
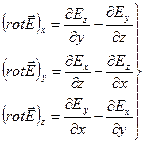 . (1.56)
. (1.56)
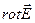 у цій системі координат описується співвідношенням:
у цій системі координат описується співвідношенням:
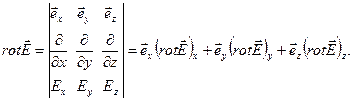 (1.56')
(1.56')
Співвідношення (1.56') враховує (1.56).
1.9.7. Теорема Стокса
Знаючи ротор вектора 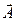 в кожній точці деякої (не обов’язково плоскої) поверхні S, можна обчислити циркуляцією цього вектора по деякому контуру Г, що охоплює поверхню S. Для цього розіб’ємо поверхню S на дуже маленькі елементи
в кожній точці деякої (не обов’язково плоскої) поверхні S, можна обчислити циркуляцією цього вектора по деякому контуру Г, що охоплює поверхню S. Для цього розіб’ємо поверхню S на дуже маленькі елементи 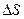 , які можна вважати плоскими. Тому, згідно з (1.54) циркуляція вектора
, які можна вважати плоскими. Тому, згідно з (1.54) циркуляція вектора 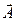 по контуру, що обмежує площу
по контуру, що обмежує площу 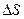 , може бути представлена у вигляді:
, може бути представлена у вигляді:
циркуляція А 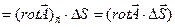 ,
,
де 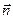 - позитивна нормаль до елементу поверхні
- позитивна нормаль до елементу поверхні 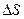 . Склавши ці вирази по всій поверхні S, і виконавши граничний перехід, за якого всі D S прагнуть до нуля, отримаємо:
. Склавши ці вирази по всій поверхні S, і виконавши граничний перехід, за якого всі D S прагнуть до нуля, отримаємо:
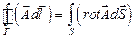 або
або 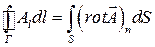 . (1.57)
. (1.57)
Співвідношення (1.57) називають теоремою Стокса.
По аналогії з (1.57) для вектора напруженості 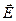 електричного поля отримаємо:
електричного поля отримаємо:
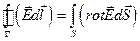 або
або 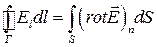 . (1.58)
. (1.58)





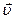 . Добуток
. Добуток 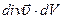 дає потужність в об’ємі
дає потужність в об’ємі 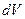 . Сума таких добутків, тобто
. Сума таких добутків, тобто 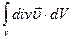 дає потужність джерел в об’ємі
дає потужність джерел в об’ємі 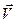 . Таким чином отримуємо співвідношення:
. Таким чином отримуємо співвідношення: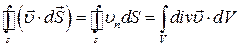 .
.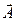 маємо:
маємо: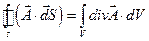 . (1.49)
. (1.49)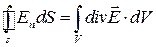 . (1.50)
. (1.50)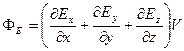 .
.
 . Припустимо, що якимось чином ми миттєво ззаморозимо рідину у всьому об’ємі, за винятком дуже тонкого замкненого каналу постійного перетину
. Припустимо, що якимось чином ми миттєво ззаморозимо рідину у всьому об’ємі, за винятком дуже тонкого замкненого каналу постійного перетину 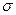 , який вміщує в себе контур
, який вміщує в себе контур  ру-
ру-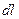 , за величиною буде дорівнювати
, за величиною буде дорівнювати 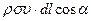 , де
, де 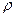 – густина рідини,
– густина рідини, 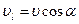 – проекція швидкості
– проекція швидкості 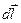 . Імпульс рідини у всьому каналі буде дорівнювати
. Імпульс рідини у всьому каналі буде дорівнювати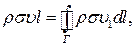 ,
,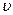 – швидкість циркуляції. Скоротивши попередній вираз на
– швидкість циркуляції. Скоротивши попередній вираз на 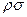 , отримаємо, що циркуляція
, отримаємо, що циркуляція 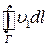 .
.
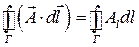 (1.51)
(1.51)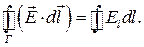 (1.52)
(1.52)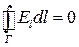 . Отже, векторне поле напруженістю
. Отже, векторне поле напруженістю 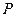 цієї поверхні, необхідно зменшувати розміри контуру, стягуючи його в точку
цієї поверхні, необхідно зменшувати розміри контуру, стягуючи його в точку 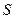 , що охоплюється контуром. Відношення циркуляції до площі
, що охоплюється контуром. Відношення циркуляції до площі 
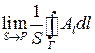 , (1.53)
, (1.53)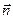 до площини контуру (позитивною вважається нормаль, зв’язана з напрямом обходу по контуру при інтегруванні правилом правого гвинта (рис.1.17). Границя (1.53) в одній і тій самій точці
до площини контуру (позитивною вважається нормаль, зв’язана з напрямом обходу по контуру при інтегруванні правилом правого гвинта (рис.1.17). Границя (1.53) в одній і тій самій точці 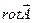 . Скориставшись цим символом, вираз (1.53) можна записати у вигляді
. Скориставшись цим символом, вираз (1.53) можна записати у вигляді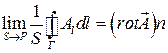 , (1.54)
, (1.54)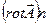 – проекція вектора
– проекція вектора 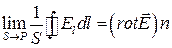 , (1.55)
, (1.55)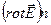 – має такий самий зміст, як і
– має такий самий зміст, як і 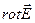 на координатні осі декартової системи мають вигляд:
на координатні осі декартової системи мають вигляд: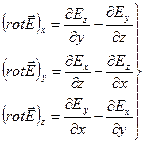 . (1.56)
. (1.56)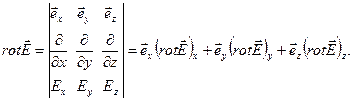 (1.56')
(1.56')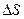 , які можна вважати плоскими. Тому, згідно з (1.54) циркуляція вектора
, які можна вважати плоскими. Тому, згідно з (1.54) циркуляція вектора 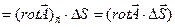 ,
,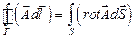 або
або 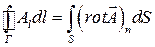 . (1.57)
. (1.57)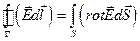 або
або 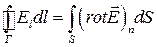 . (1.58)
. (1.58)


