Для опису властивостей векторних полів, в тім числі і електричного, зручно використати математичний апарат – так званий векторний аналіз. Одним із елементів цього аналізу є градієнт, який використовують для скалярних полів. Якщо кожній точці з координатами 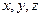 співставляється значення скалярної величини
співставляється значення скалярної величини 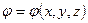 , то кажуть, що задано скалярне поле
, то кажуть, що задано скалярне поле 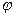 . Градієнтом величини
. Градієнтом величини 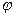 називають вектор
називають вектор
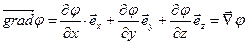 .
.
Для електростатичного поля 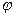 - потенціал поля (див.(1.23)-(1.25)).
- потенціал поля (див.(1.23)-(1.25)).
При зміщенні на відрізок 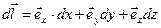 зміна функції
зміна функції 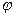 дорівнює
дорівнює
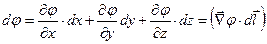 .
.
Розглянемо деякі інші елементи.
1.9.1. Потік вектора напруженості електричного поля 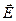
Скористаємося моделлю текучої рідини. Нехай течія рідини характе- ризується полем вектора швидкості 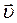 . Об’єм
. Об’єм 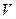 рідини, що протікає в оди- ницю часу через деяку уявну поверхню
рідини, що протікає в оди- ницю часу через деяку уявну поверхню 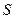 , називають потоком рідини через цю поверхню. Очевидно, що за проміжок часу
, називають потоком рідини через цю поверхню. Очевидно, що за проміжок часу 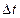 через плоску поверхню
через плоску поверхню 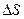 протікає об’єм рідини
протікає об’єм рідини 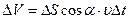 (рис.1.12).
(рис.1.12).
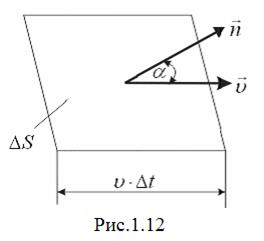
Розділивши цей об’єм на проміжок часу 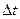 , знайдемо потік рідини через поверхню
, знайдемо потік рідини через поверхню 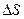 :
:
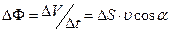 .
.
Через елементарну поверхню 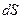 довільної форми потік рідини
довільної форми потік рідини
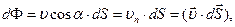 (1.38)
(1.38)
де 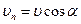 - проекція вектора
- проекція вектора 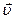 на нормаль
на нормаль 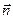 ,
, 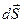 - не істинний, а псевдовектор.
- не істинний, а псевдовектор.
Склавши потоки через всі елементарні поверхні, на які була поділена поверхня 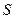 , знайдемо потік рідини через всю поверхню
, знайдемо потік рідини через всю поверхню 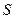 :
:
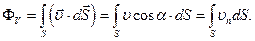 (1.39)
(1.39)
Для будь-якого вектора 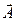 величину
величину
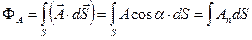 (1.40)
(1.40)
називають потоком вектора 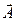 через поверхню
через поверхню 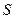 . Отже, формула (1.39) описує потік вектора
. Отже, формула (1.39) описує потік вектора 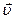 через поверхню
через поверхню 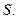
По аналогії з (1.38) – (1.40) для вектора напруженості 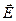 електричного поля отримаємо:
електричного поля отримаємо:
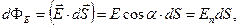 (1.41)
(1.41)
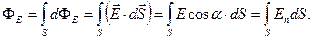 (1.42)
(1.42)
Теорема Гаус c а
 Німецький вчений Гаусс на початку 19ст. довів, що потік вектора напружено- сті електричного поля через замкнену поверхню пропорційний сумарному заряду під цією поверхнею:
Німецький вчений Гаусс на початку 19ст. довів, що потік вектора напружено- сті електричного поля через замкнену поверхню пропорційний сумарному заряду під цією поверхнею: 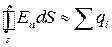 (1.43)
(1.43)
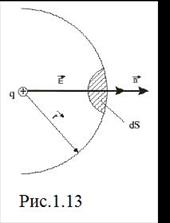
Це твердження називають теоремою Гаусса. Розглянемо цю теорему на прикладі поля точкового заряду, охопленого концентричною сферичною поверхнею радіуса 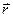 (рис.1.13).
(рис.1.13).
Нормаль 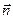 до такої поверхні співпадає з радіусом
до такої поверхні співпадає з радіусом 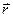 . Оскільки поле точкового заряду центральносиметричне , то
. Оскільки поле точкового заряду центральносиметричне , то
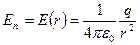 .
.
Тоді
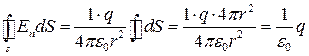 ,
,
що узгоджується з (1.43). Отриманий результат залишається справедливим і для поверхні довільної форми. Насправді, потік вектора 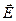 через поверхню
через поверхню 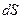 (рис.1.14) дорівнює:
(рис.1.14) дорівнює:
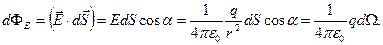
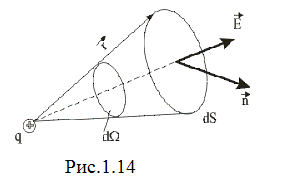 Тут
Тут 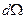 - елементарний тілесний кут. Потік через замкнену поверхню
- елементарний тілесний кут. Потік через замкнену поверхню
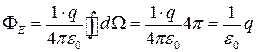 ,
,
що теж узгоджується з теоремою Гаусса.
Якщо під замкненою поверхнею знаходяться 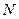 точкових зарядів, то згідно з принципом суперпозиції, напруженість поля
точкових зарядів, то згідно з принципом суперпозиції, напруженість поля 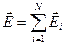 .Тому
.Тому
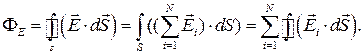 .
.
Кожен із інтегралів під знаком суми дорівнює 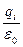 . Отже,
. Отже,
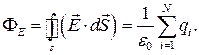 (1.44)
(1.44)
У випадку об’ємних 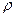 і поверхневих
і поверхневих 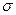 безперервно розподілених зарядів формула (1.44) узагальнюється так:
безперервно розподілених зарядів формула (1.44) узагальнюється так:
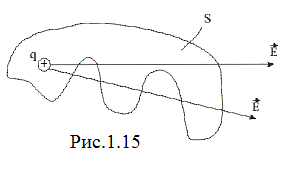
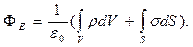 (1.45)
(1.45)
В СІ коефіцієнт пропорційності в теоремі Гаусcа дорівнює 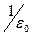 .
.
Якщо замкнена поверхня будь-якої форми не охоплює заряди, то 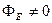 , оскільки кожна лінія
, оскільки кожна лінія 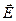 перетинає поверхню непарне число разів (рис.1.15).
перетинає поверхню непарне число разів (рис.1.15).
1.9.3. Дивергенція (розходження) вектора 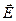
Потік вектора 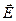 через замкнену поверхню, що відображає принцип суперпозиції, є інтегральною властивістю поля у всьому об’ємі, обмеженому цією поверхнею. Для характеристики поля у будь-якій точці використовують поняття дивергенції вектора
через замкнену поверхню, що відображає принцип суперпозиції, є інтегральною властивістю поля у всьому об’ємі, обмеженому цією поверхнею. Для характеристики поля у будь-якій точці використовують поняття дивергенції вектора 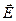 .
.
Якщо потік будь-якого вектора (наприклад вектора швидкості рідини) через замкнену поверхню не дорівнює нулеві, то в об’ємі під поверхнею є джерела або стоки рідини, тобто точки, в яких рідина поступає в об’єм (джерела), або витікає із об’єму (стоки). Величина потоку визначає сумарну потужність джерел і стоків (з загальною назвою джерел).
Відношення потоку до величини об’єму, із якого він витікає, тобто 
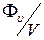 дає середню питому потужність джерел, що знаходяться в цьому об’ємі. У векторному аналізі доведено, що границя відношення потоку будь-якого вектора
дає середню питому потужність джерел, що знаходяться в цьому об’ємі. У векторному аналізі доведено, що границя відношення потоку будь-якого вектора 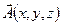 , визначеного у всіх точках векторного поля, крізь замкнену поверхню
, визначеного у всіх точках векторного поля, крізь замкнену поверхню 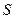 до об’єму
до об’єму 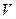 , обмеженого цією поверхнею, при
, обмеженого цією поверхнею, при 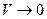 (при стягуванні об’єму в точку
(при стягуванні об’єму в точку 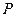 ) не залежить від форми
) не залежить від форми 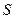 . Границя цього відношення визначає дійсну питому потужність джерел в цій точці
. Границя цього відношення визначає дійсну питому потужність джерел в цій точці 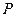 . Ця потужність і є характеристикою векторного поля в точці
. Ця потужність і є характеристикою векторного поля в точці 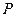 . Її називають дивергенцією або розходженням вектора
. Її називають дивергенцією або розходженням вектора 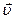 і позначають
і позначають 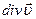 .
.
Таким чином, за визначенням
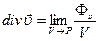 .
.
Для будь-якого вектора 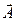
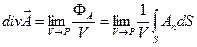 . (1.46)
. (1.46)
Аналогічно формулі (1.46) дивергенція вектора 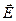 дорівнює:
дорівнює:
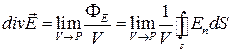 . (1.47)
. (1.47)
Якщо сумарний заряд під замкнутою поверхнею розподілений з об’ємною густиною 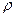 , то, згідно з теоремою Гаусса (1.44)
, то, згідно з теоремою Гаусса (1.44)
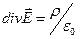 .
.
Із вище сказаного (див.(1.42), (1.47)) випливає, що і потік і дивергенція є величинами скалярними.
У декартовій системі координат
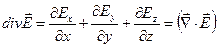 (1.48)
(1.48)





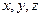 співставляється значення скалярної величини
співставляється значення скалярної величини 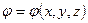 , то кажуть, що задано скалярне поле
, то кажуть, що задано скалярне поле 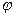 . Градієнтом величини
. Градієнтом величини 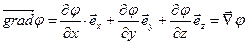 .
.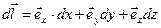 зміна функції
зміна функції 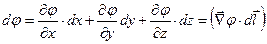 .
.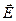
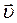 . Об’єм
. Об’єм 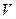 рідини, що протікає в оди- ницю часу через деяку уявну поверхню
рідини, що протікає в оди- ницю часу через деяку уявну поверхню 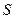 , називають потоком рідини через цю поверхню. Очевидно, що за проміжок часу
, називають потоком рідини через цю поверхню. Очевидно, що за проміжок часу 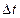 через плоску поверхню
через плоску поверхню 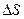 протікає об’єм рідини
протікає об’єм рідини 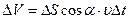 (рис.1.12).
(рис.1.12). 
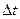 , знайдемо потік рідини через поверхню
, знайдемо потік рідини через поверхню 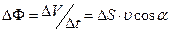 .
.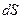 довільної форми потік рідини
довільної форми потік рідини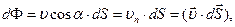 (1.38)
(1.38) 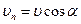 - проекція вектора
- проекція вектора 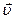 на нормаль
на нормаль 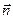 ,
, 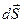 - не істинний, а псевдовектор.
- не істинний, а псевдовектор.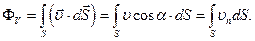 (1.39)
(1.39)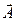 величину
величину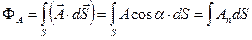 (1.40)
(1.40)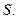
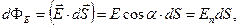 (1.41)
(1.41)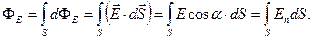 (1.42)
(1.42) Німецький вчений Гаусс на початку 19ст. довів, що потік вектора напружено- сті електричного поля через замкнену поверхню пропорційний сумарному заряду під цією поверхнею:
Німецький вчений Гаусс на початку 19ст. довів, що потік вектора напружено- сті електричного поля через замкнену поверхню пропорційний сумарному заряду під цією поверхнею: 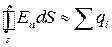 (1.43)
(1.43) 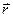 (рис.1.13).
(рис.1.13).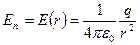 .
.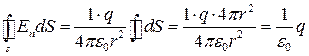 ,
,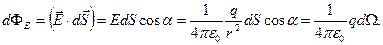
 Тут
Тут 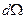 - елементарний тілесний кут. Потік через замкнену поверхню
- елементарний тілесний кут. Потік через замкнену поверхню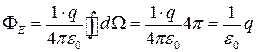 ,
,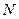 точкових зарядів, то згідно з принципом суперпозиції, напруженість поля
точкових зарядів, то згідно з принципом суперпозиції, напруженість поля 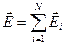 .Тому
.Тому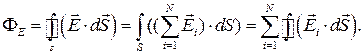 .
.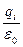 . Отже,
. Отже,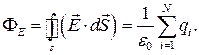 (1.44)
(1.44)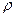 і поверхневих
і поверхневих 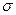 безперервно розподілених зарядів формула (1.44) узагальнюється так:
безперервно розподілених зарядів формула (1.44) узагальнюється так:
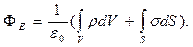 (1.45)
(1.45)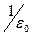 .
.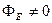 , оскільки кожна лінія
, оскільки кожна лінія 
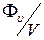 дає середню питому потужність джерел, що знаходяться в цьому об’ємі. У векторному аналізі доведено, що границя відношення потоку будь-якого вектора
дає середню питому потужність джерел, що знаходяться в цьому об’ємі. У векторному аналізі доведено, що границя відношення потоку будь-якого вектора 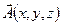 , визначеного у всіх точках векторного поля, крізь замкнену поверхню
, визначеного у всіх точках векторного поля, крізь замкнену поверхню 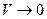 (при стягуванні об’єму в точку
(при стягуванні об’єму в точку 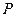 ) не залежить від форми
) не залежить від форми 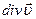 .
.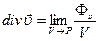 .
.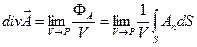 . (1.46)
. (1.46)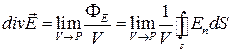 . (1.47)
. (1.47)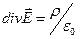 .
.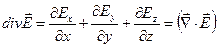 (1.48)
(1.48)


