технических средств
Расчет параметров вращательного движения
Задача № 1
Частота вращения колеса лопаточного типа вентилятора в салоне транспортного средства равна 300 об/мин. В момент времени t 0 = 0 оно начинает двигаться равнозамедленно, с угловым ускорением – 0,2 рад/с2. С какой частотой будет вращаться колесо через 1 мин?
Представим условие задачи в формализованном виде: n 0 = 300 об/мин; 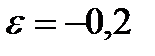 рад/с2; t = 1 мин = 60 с; определить n.
рад/с2; t = 1 мин = 60 с; определить n.
Решение.
Для определения n воспользуемся формулами: 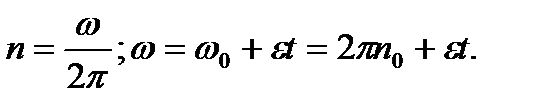 Тогда
Тогда 
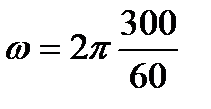 [об/с] –
[об/с] – 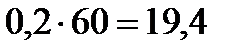 [рад/с];
[рад/с];
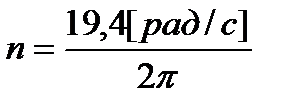 [об/с] =
[об/с] = 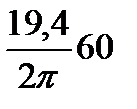 [об/мин] =
[об/мин] = 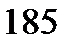 об/мин.
об/мин.
Задача № 2
К ободу однородного сплошного диска, являющегося деталью одного из агрегатов станции технического обслуживания, приложена касательная сила 100 Н. Радиус диска – 0,5 м. При вращении диска на него действует момент сил трения 2 Н.м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 12 рад/с2.
Решение.
Условие задачи в формализованном виде: r = 0,5 м, Pu = 100 Н, M тр = 2 Н.м, 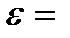 12 рад/с2; определить m. Для решения задачи воспользуемся формулой
12 рад/с2; определить m. Для решения задачи воспользуемся формулой 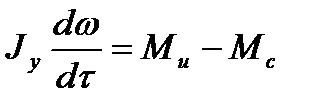 или
или 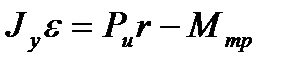 . Известно, что для диска
. Известно, что для диска 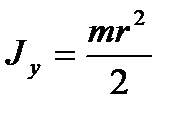 ; тогда получим
; тогда получим 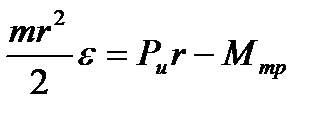 ; отсюда
; отсюда 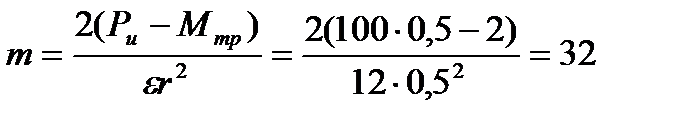 кг.
кг.
Задача № 3
Скорость вращения колеса в редукторе погрузочного конвейера в течение 1 минуты уменьшилась с 300 об/мин до 180 об/мин. Вращение колеса при торможении равнозамедленное. Момент инерции колеса 2 кгм2. Определить:
1) угловое ускорение колеса; 2) момент силы торможения; 3) работу силы торможения.
Решение.
Условие задачи в формализованном виде: 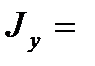 2 кгм2;
2 кгм2;
t = 1 мин; n 1= 300 об/мин; n 2 =180 об/мин; определить 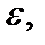 М торм., L торм..
М торм., L торм..
1. Определение углового ускорения колеса: 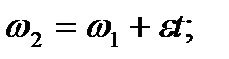
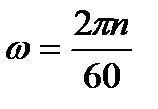 рад/с;
рад/с;
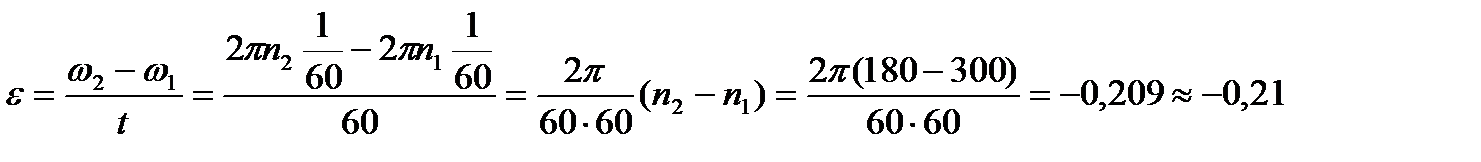 рад/с2.
рад/с2.
2. Определение момента силы торможения: 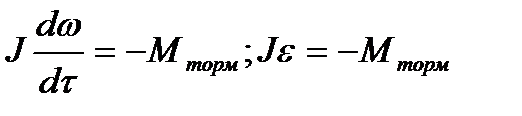 ;
;
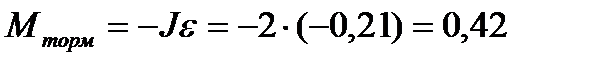 Нм.
Нм.
3. Определение работы силы торможения. Работа силы торможения равна изменению кинетической энергии колеса при уменьшении его угловой скорости с 300 об/мин до 180 об/мин за время t = 1 мин. Кинетическая энергия вращающегося тела равна сумме кинетических энергий всех точек тела
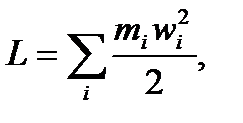
где 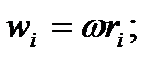 mi – масса i -й точки тела; ri – расстояние (радиус) от i -й точки тела до оси (колеса); wi – линейная скорость i -й точки.
mi – масса i -й точки тела; ri – расстояние (радиус) от i -й точки тела до оси (колеса); wi – линейная скорость i -й точки.
Тогда
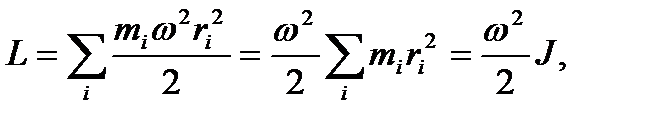
где 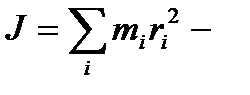 момент инерции тела относительно оси.
момент инерции тела относительно оси.
Поэтому
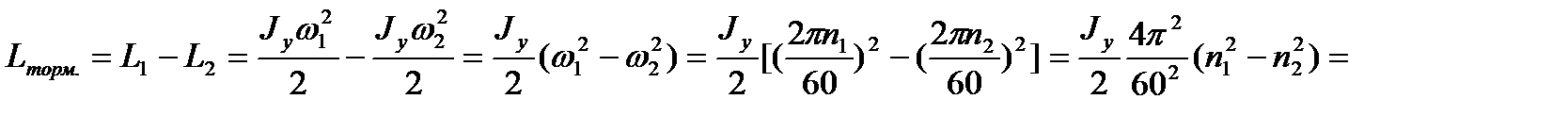
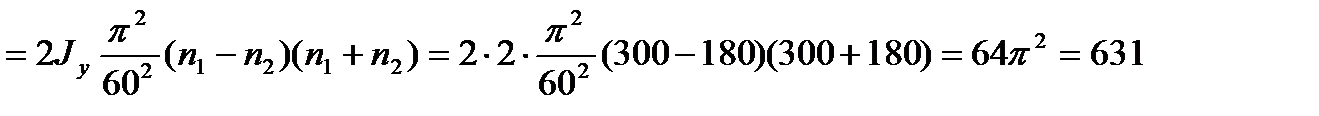 Дж.
Дж.
Расчет сил трения при поступательном движении
транспортных средств
Задача № 1
Железнодорожный двухосный вагон массой 10 тонн скатывается с сортировочной горки и, двигаясь равноускоренно с ускорением 0,5 м/с2, достигает горизонтального участка пути через 12 секунд. Другой такой же вагон, но прошедший техническое обслуживание с заменой смазки в подшипниках скольжения, скатывается с этой же горки за 10 секунд.
Определить, как изменилась сила трения в подшипниках скольжения в результате технического обслуживания.
Решение.
Представим условие задачи в формализованном виде: m = 10 т = 10.103 = 104 кг; a 1 = 0,5 м/с2; t 1 = 12 с; t 2 = 10 с. Требуется определить 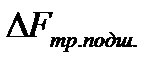 .
.
1. В соответствии со вторым законом механики
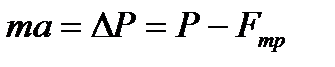 и
и 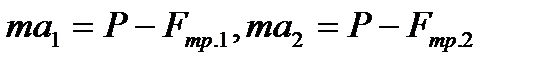 для первого и второго вагонов соответственно. Отсюда
для первого и второго вагонов соответственно. Отсюда 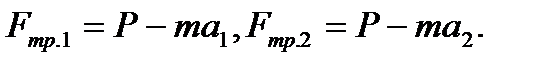 Уменьшение суммарной силы трения всех подшипников скольжения вагона составит
Уменьшение суммарной силы трения всех подшипников скольжения вагона составит
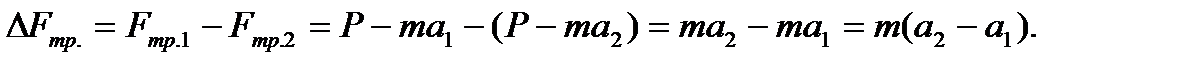 Уменьшение силы трения в одном подшипнике составит
Уменьшение силы трения в одном подшипнике составит
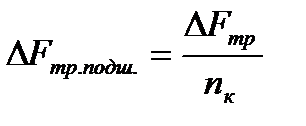 ,
,
где n к – число колес в вагоне (для двухосного вагона n к = 4).
С учетом выражения для 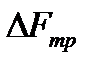 имеем
имеем
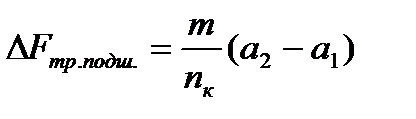 .
.
2. Определим теперь величину a 2. Для этого воспользуемся общим выражением для линейной скорости равноускоренного движения
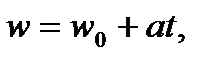
где w 0 – начальная скорость; в нашей задаче w 0 = 0, и w = at.
Определим длину сортировочной горки l, используя соотношение
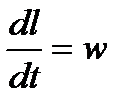 или
или 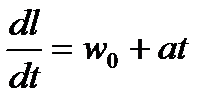 и dl = w 0 dt + at dt. Интегрируя последнее выражение, получим
и dl = w 0 dt + at dt. Интегрируя последнее выражение, получим
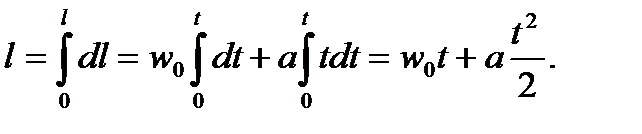
Выражая l через a 1, t 1 и a 2, t 2, имеем:
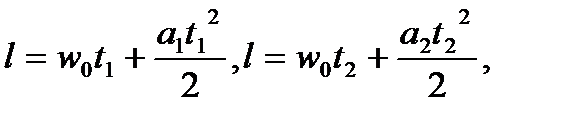 а для случая w 0 = 0 получим
а для случая w 0 = 0 получим
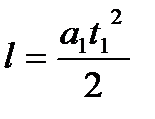 и
и 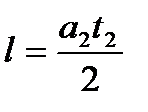 . Отсюда a1 t12 = a2 t22 и
. Отсюда a1 t12 = a2 t22 и 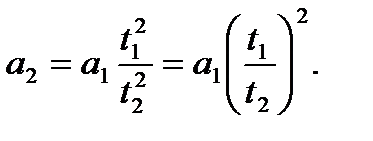
3. Подставляя это выражение в последнюю формулу для 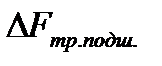 , имеем:
, имеем: 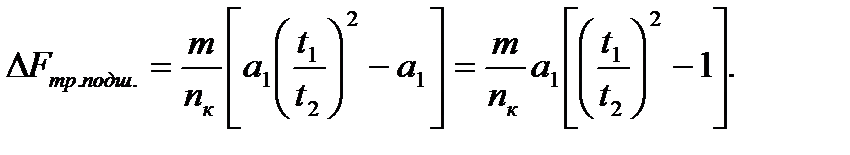
4. Вычислим 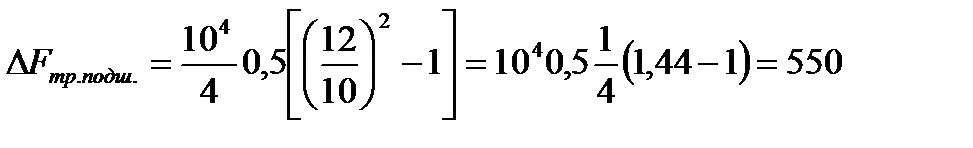 Н.
Н.
Задача № 2
Какова сила трения при движении колеса четырехосной платформы массой 16 тонн, если смещение k = 0,01 м, а радиус колеса – 0,5 м?
Решение.
Представим условие задачи в формализованном виде: m = 16 т = 16. 103 кг; k = 0,01 м; rk = 0,5; nk = 8. Требуется определить F тр.
Воспользуемся формулой для определения силы трения качения
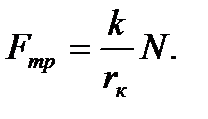
В соответствии с условием задачи здесь N – нормальная сила, определяемая силой тяжести платформы, приходящаяся на одно колесо. Поэтому
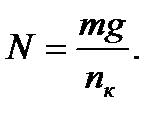
Отметим, что у четырехосной платформы количество колес n к = 8.
Окончательно получим
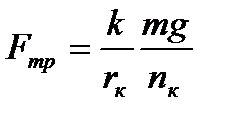
и 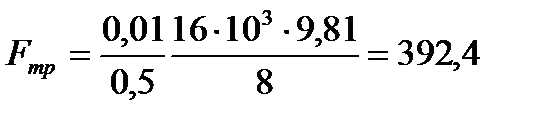 Н.
Н.
Задача № 3
Как надо изменить радиус колеса, чтобы трение качения при его движении уменьшилось на 20%? (Масса колеса неизменна).
Решение.
Представим условие задачи в формализованном виде: радиус колеса r к1;
относительное уменьшение силы трения 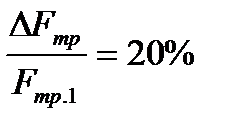 ;
; 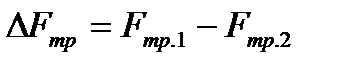 ; здесь F тр.1 соответствует колесу с радиусом r к1, а F тр.2 – колесу с измененным радиусом, т.е. с r к2; определить r к2.
; здесь F тр.1 соответствует колесу с радиусом r к1, а F тр.2 – колесу с измененным радиусом, т.е. с r к2; определить r к2.
Согласно формуле для силы трения качения можем записать: 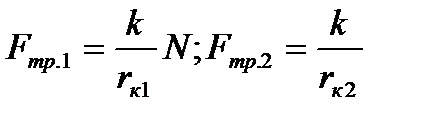 N. Тогда
N. Тогда 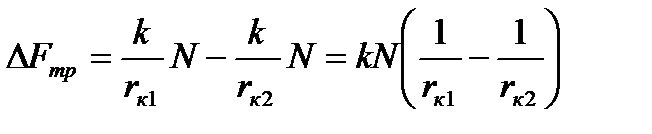 . Теперь можем получить выражение для
. Теперь можем получить выражение для 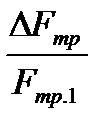 :
:
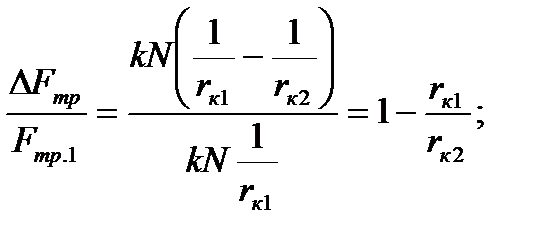 отсюда
отсюда 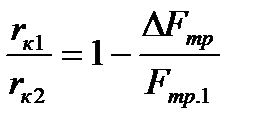 и
и 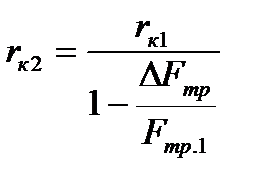 .
.
Так как 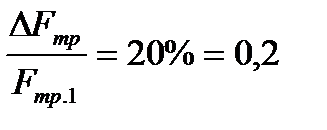 , то
, то 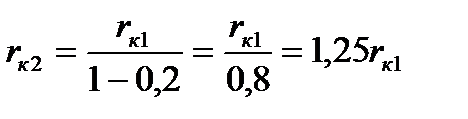 , т.е. необходимо радиус колеса увеличить в 1,25 раза.
, т.е. необходимо радиус колеса увеличить в 1,25 раза.
Рассмотрим примеры расчета сил сопротивления среды.
Задача № 1
Модернизированный вариант танкера характеризуется повышением максимальной массы перевозимого груза на 20%. Площадь смачиваемой поверхности танкера увеличилась на 15%, а скорость уменьшилась на 10%. Как изменилась сила гидродинамического сопротивления? (Коэффициент Cw практически не изменился, его можно принять постоянным для данного класса судов.)
Решение.
Введем обозначения: m 1 – масса танкера с грузом до его модернизации; m 2 – масса танкера с грузом после модернизации; S 1, S 2 – площадь смачиваемой поверхности танкера до и после модернизации соответственно; w 1, w 2 – скорость танкера до и после модернизации соответственно; Fc 1, Fc 2 – сила гидродинамического сопротивления танкера до и после модернизации соответственно. Требуется определить Fc 2 / Fc 1 или 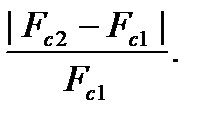
В соответствии с условием задачи можем записать: m 2 = m 1 + 0,2 m 1 = 1,2 m 1; S 2 = S 1 + 0,15 S 1 = 1,15 S 1; w 2 = w 1 – 0,1 w 1 = 0,9 w 1. На основании формулы 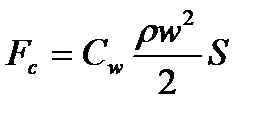 получим
получим 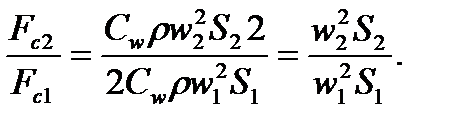 После подстановки в эту формулу значений w 2 и S 2, выраженных через w 1 и S 1, получим
После подстановки в эту формулу значений w 2 и S 2, выраженных через w 1 и S 1, получим
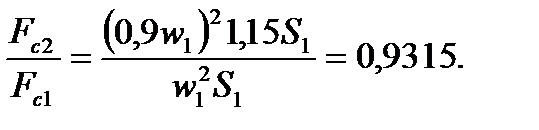 Отсюда Fc 2 = 0,9315 Fc 1; Fc 2 < Fc 1. Следовательно, сила гидродинамического сопротивления уменьшилась на
Отсюда Fc 2 = 0,9315 Fc 1; Fc 2 < Fc 1. Следовательно, сила гидродинамического сопротивления уменьшилась на
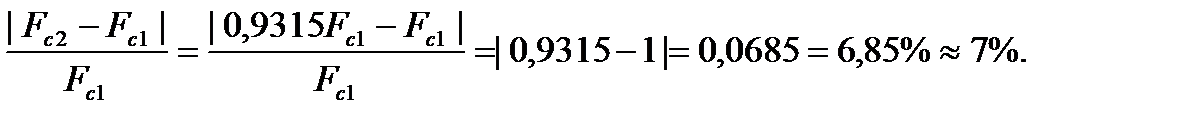
Задача № 2
Скорость полета самолета на высоте 500 м составляет 720 км/ч. Определить силу сопротивления крылу самолета, если площадь миделевого сечения крыла 1,7 м2, коэффициент лобового сопротивления 0,04, плотность воздуха на высоте 500 м составляет 1,167 кг/м3.
Решение.
Представим условие задачи в формализованном виде:
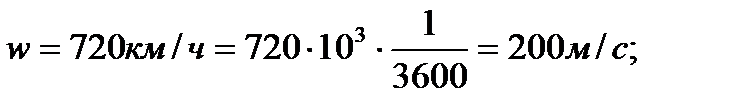
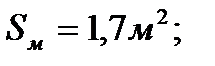
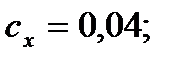
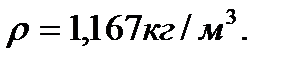
Определить F аэр.
В формулу 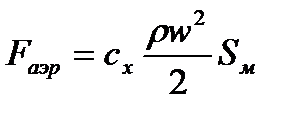 подставим соответствующие численные значения:
подставим соответствующие численные значения: 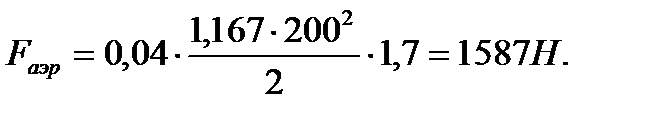
Задача № 3
Как следует изменить площадь миделевого сечения крыла (в условиях задачи №2), чтобы, не увеличивая тягу двигателя, увеличить скорость до 750 км/ч?
Решение.
Представим условие задачи в формализованном виде:
cx = 0,04; S м1 = 1,7 м2; 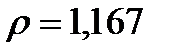 кг/м2; w = 750 км/ч; F аэр = 1587 Н. Определить S м и
кг/м2; w = 750 км/ч; F аэр = 1587 Н. Определить S м и 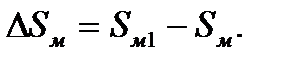
Из формулы для F аэр находим 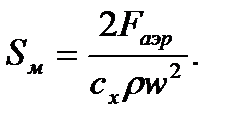 Подставим в эту формулу численные значения:
Подставим в эту формулу численные значения: 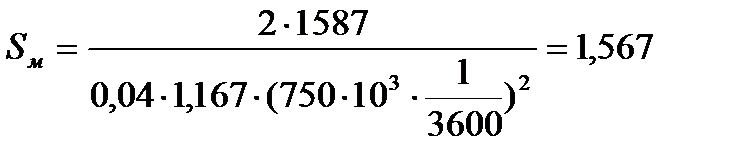 м2. Тогда
м2. Тогда
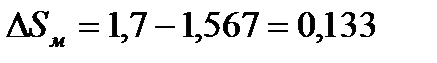 м2.
м2.
Задачи термодинамики
Задача № 1
В нормальных условиях эксплуатации транспортного средства давление сжатого газа в баллоне равно 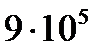 Па при температуре 295 К. Определить давление газа в баллоне при аварийном повышении температуры окружающей среды до 317 оС.
Па при температуре 295 К. Определить давление газа в баллоне при аварийном повышении температуры окружающей среды до 317 оС.
Представим условие задачи в формализованном виде:
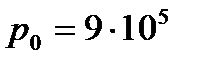 Па; Т0 =295 К; t 1 = 317 оС.Определить р1.
Па; Т0 =295 К; t 1 = 317 оС.Определить р1.
В соответствии с уравнением состояния газов можем записать:
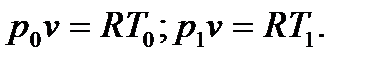 Разделим первое уравнение на второе и получим:
Разделим первое уравнение на второе и получим:
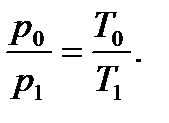
Отсюда 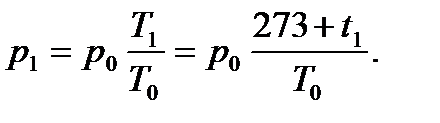 Подставляя численные значения, получаем:
Подставляя численные значения, получаем: 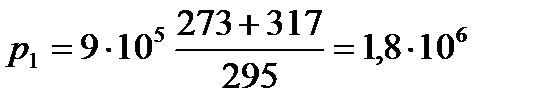 Па.
Па.
Задача № 2
Масса сжатого газа (аммиака) в баллоне емкостью 100 л равна 0,25 кг. Каково давление газа в баллоне при температуре 295 К? Не разрушится ли баллон при температуре 590 К, если предельно допустимое давление составляет 106 Па?
Представим условие задачи в формализованном виде: m = 0,25; NH3 – аммиак; V = 100 л; p * = 106 Па; Т = 295 К; Т1 = 590 К. Определить p, p 1.
На основании уравнения состояния газов получим 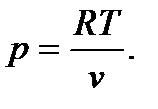 Входящие в формулу неизвестные параметры найдем с помощью соответствующих соотношений:
Входящие в формулу неизвестные параметры найдем с помощью соответствующих соотношений:
для газовой постоянной – 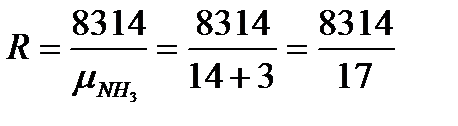 (Дж/кгК);
(Дж/кгК);
для удельного объема – 
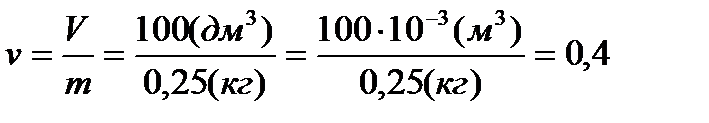 м3/кг.
м3/кг.
Теперь определим p: 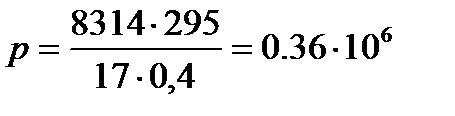 Па. Для определения p 1 используем уравнение состояния газов: pv = RT; p 1 v = RT 1.
Па. Для определения p 1 используем уравнение состояния газов: pv = RT; p 1 v = RT 1.
После деления второго уравнения на первое получим
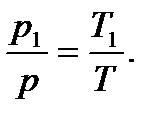 Отсюда
Отсюда 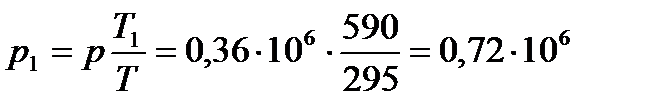 Па < p * = 106. Следовательно, баллон не разрушится.
Па < p * = 106. Следовательно, баллон не разрушится.





 рад/с2; t = 1 мин = 60 с; определить n.
рад/с2; t = 1 мин = 60 с; определить n.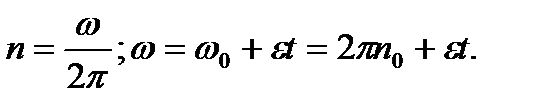 Тогда
Тогда 
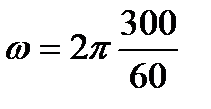 [об/с] –
[об/с] – 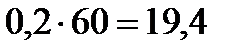 [рад/с];
[рад/с];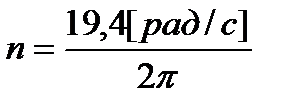 [об/с] =
[об/с] = 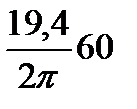 [об/мин] =
[об/мин] = 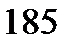 об/мин.
об/мин. 12 рад/с2; определить m. Для решения задачи воспользуемся формулой
12 рад/с2; определить m. Для решения задачи воспользуемся формулой 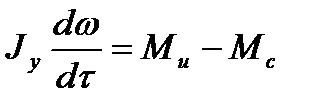 или
или 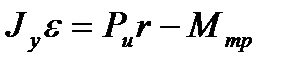 . Известно, что для диска
. Известно, что для диска 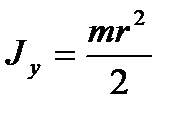 ; тогда получим
; тогда получим 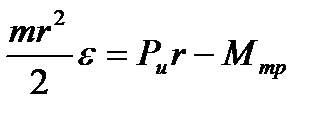 ; отсюда
; отсюда 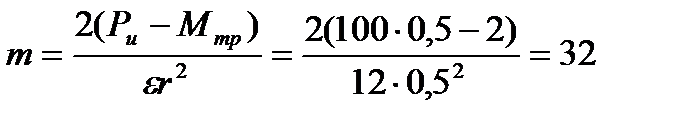 кг.
кг.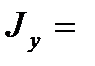 2 кгм2;
2 кгм2;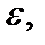 М торм., L торм..
М торм., L торм..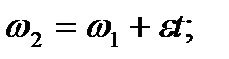
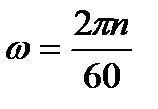 рад/с;
рад/с;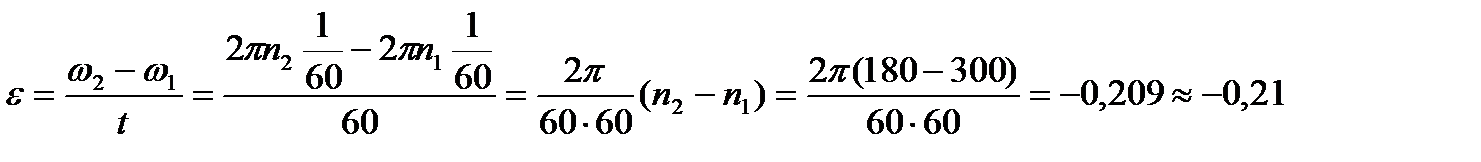 рад/с2.
рад/с2.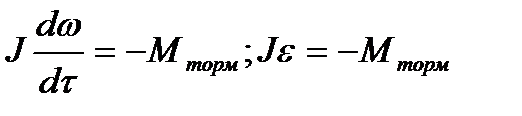 ;
;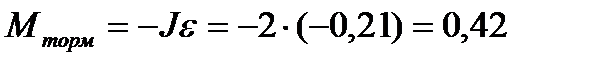 Нм.
Нм.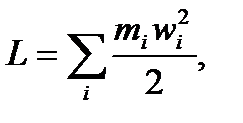
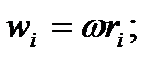 mi – масса i -й точки тела; ri – расстояние (радиус) от i -й точки тела до оси (колеса); wi – линейная скорость i -й точки.
mi – масса i -й точки тела; ri – расстояние (радиус) от i -й точки тела до оси (колеса); wi – линейная скорость i -й точки.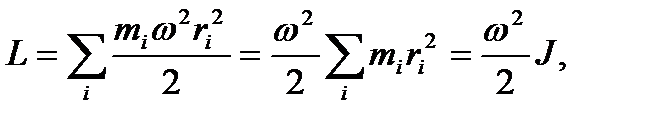
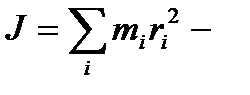 момент инерции тела относительно оси.
момент инерции тела относительно оси.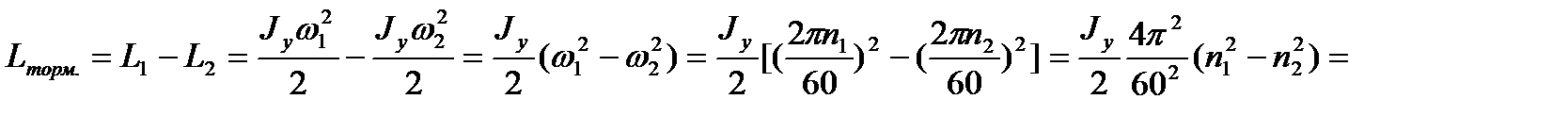
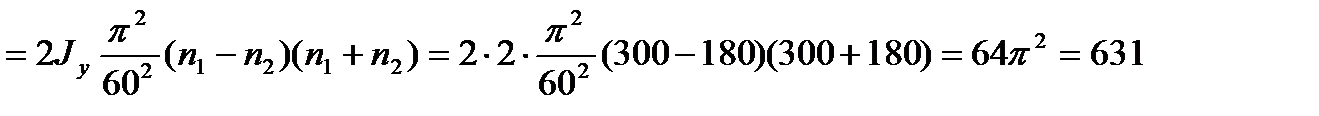 Дж.
Дж. .
.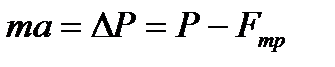 и
и 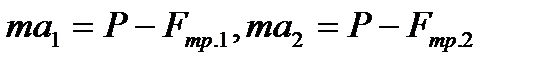 для первого и второго вагонов соответственно. Отсюда
для первого и второго вагонов соответственно. Отсюда 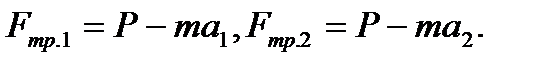 Уменьшение суммарной силы трения всех подшипников скольжения вагона составит
Уменьшение суммарной силы трения всех подшипников скольжения вагона составит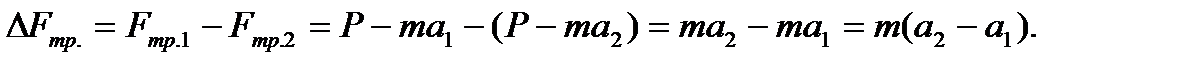 Уменьшение силы трения в одном подшипнике составит
Уменьшение силы трения в одном подшипнике составит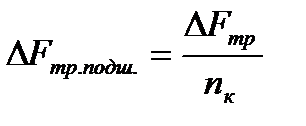 ,
,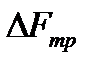 имеем
имеем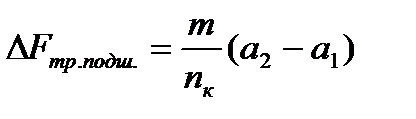 .
.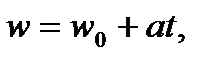
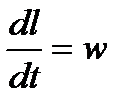 или
или 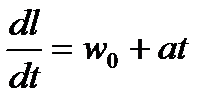 и dl = w 0 dt + at dt. Интегрируя последнее выражение, получим
и dl = w 0 dt + at dt. Интегрируя последнее выражение, получим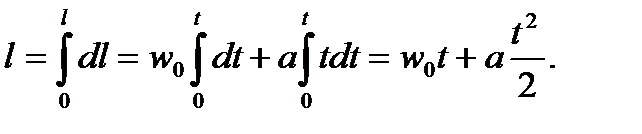
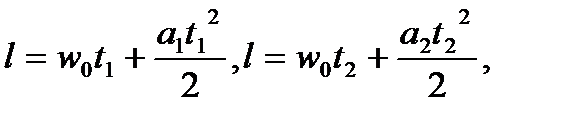 а для случая w 0 = 0 получим
а для случая w 0 = 0 получим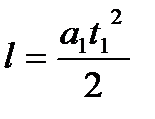 и
и 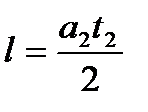 . Отсюда a1 t12 = a2 t22 и
. Отсюда a1 t12 = a2 t22 и 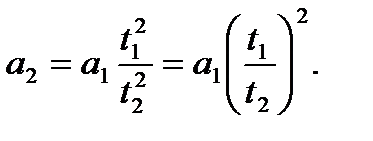
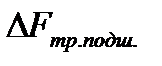 , имеем:
, имеем: 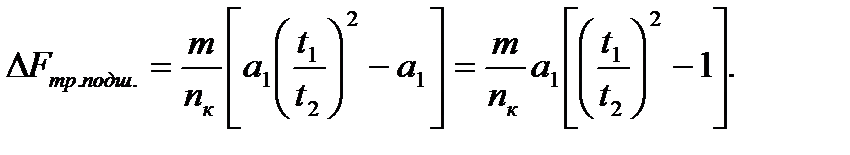
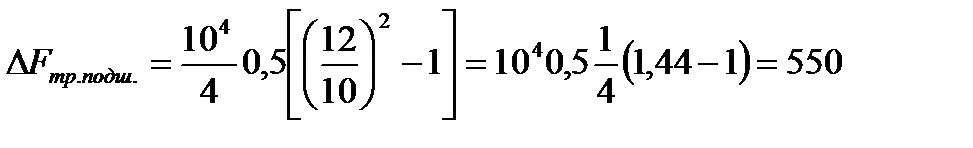 Н.
Н.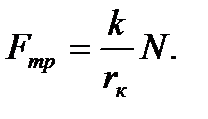
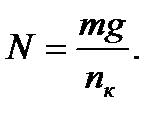
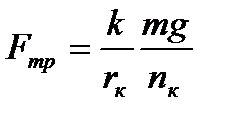
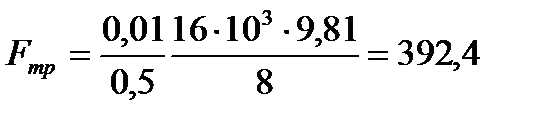 Н.
Н.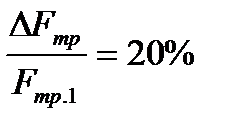 ;
; 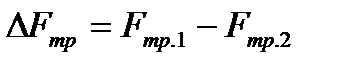 ; здесь F тр.1 соответствует колесу с радиусом r к1, а F тр.2 – колесу с измененным радиусом, т.е. с r к2; определить r к2.
; здесь F тр.1 соответствует колесу с радиусом r к1, а F тр.2 – колесу с измененным радиусом, т.е. с r к2; определить r к2.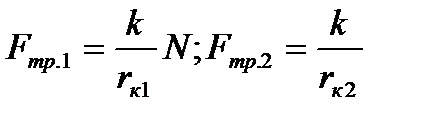 N. Тогда
N. Тогда 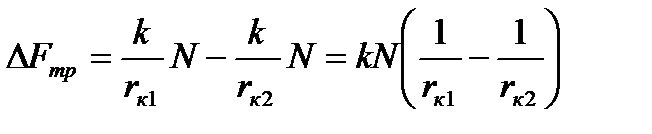 . Теперь можем получить выражение для
. Теперь можем получить выражение для 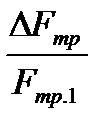 :
: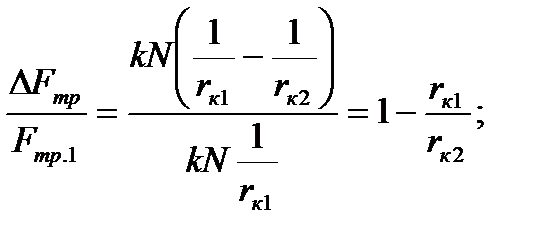 отсюда
отсюда 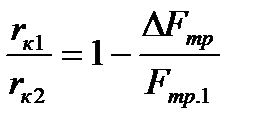 и
и 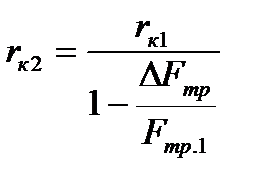 .
.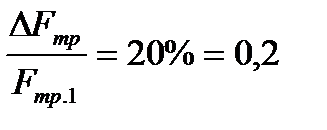 , то
, то 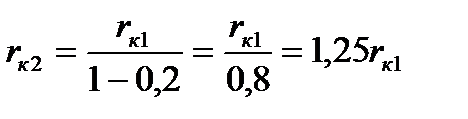 , т.е. необходимо радиус колеса увеличить в 1,25 раза.
, т.е. необходимо радиус колеса увеличить в 1,25 раза.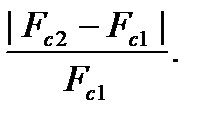
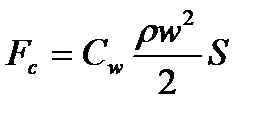 получим
получим 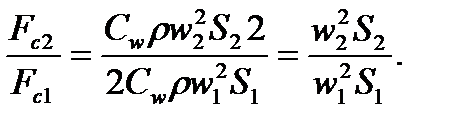 После подстановки в эту формулу значений w 2 и S 2, выраженных через w 1 и S 1, получим
После подстановки в эту формулу значений w 2 и S 2, выраженных через w 1 и S 1, получим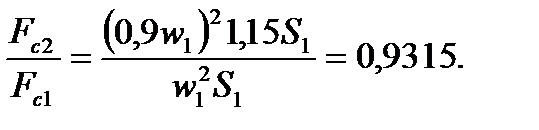 Отсюда Fc 2 = 0,9315 Fc 1; Fc 2 < Fc 1. Следовательно, сила гидродинамического сопротивления уменьшилась на
Отсюда Fc 2 = 0,9315 Fc 1; Fc 2 < Fc 1. Следовательно, сила гидродинамического сопротивления уменьшилась на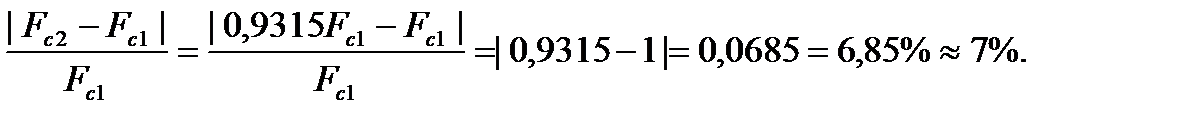
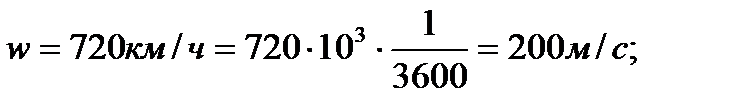
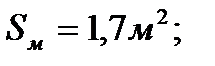
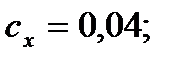
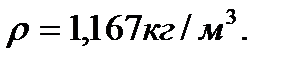
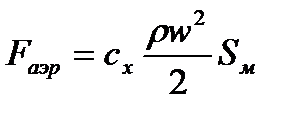 подставим соответствующие численные значения:
подставим соответствующие численные значения: 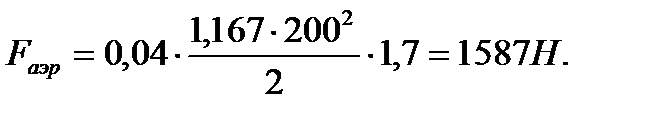
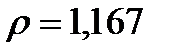 кг/м2; w = 750 км/ч; F аэр = 1587 Н. Определить S м и
кг/м2; w = 750 км/ч; F аэр = 1587 Н. Определить S м и 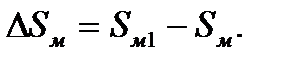
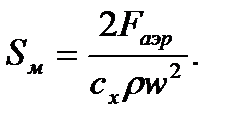 Подставим в эту формулу численные значения:
Подставим в эту формулу численные значения: 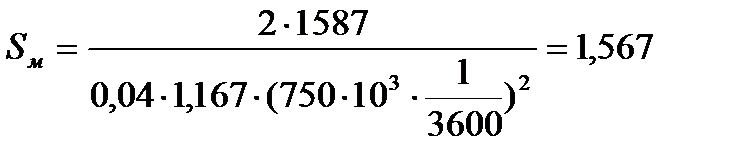 м2. Тогда
м2. Тогда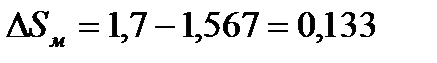 м2.
м2.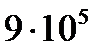 Па при температуре 295 К. Определить давление газа в баллоне при аварийном повышении температуры окружающей среды до 317 оС.
Па при температуре 295 К. Определить давление газа в баллоне при аварийном повышении температуры окружающей среды до 317 оС.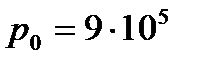 Па; Т0 =295 К; t 1 = 317 оС.Определить р1.
Па; Т0 =295 К; t 1 = 317 оС.Определить р1.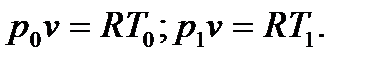 Разделим первое уравнение на второе и получим:
Разделим первое уравнение на второе и получим: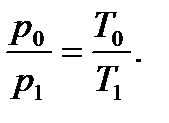
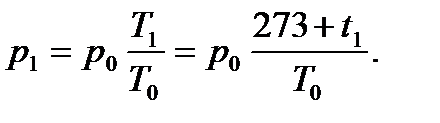 Подставляя численные значения, получаем:
Подставляя численные значения, получаем: 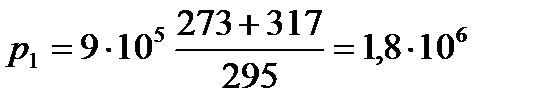 Па.
Па.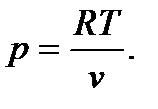 Входящие в формулу неизвестные параметры найдем с помощью соответствующих соотношений:
Входящие в формулу неизвестные параметры найдем с помощью соответствующих соотношений: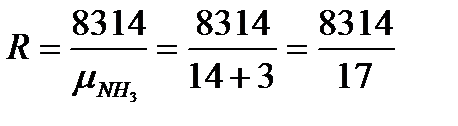 (Дж/кгК);
(Дж/кгК);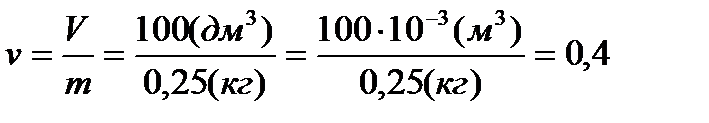 м3/кг.
м3/кг.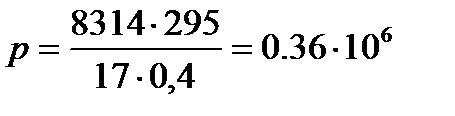 Па. Для определения p 1 используем уравнение состояния газов: pv = RT; p 1 v = RT 1.
Па. Для определения p 1 используем уравнение состояния газов: pv = RT; p 1 v = RT 1.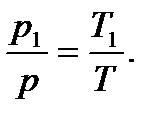 Отсюда
Отсюда 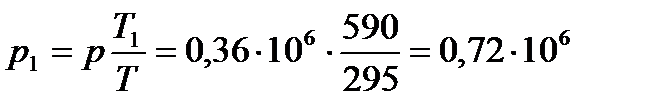 Па < p * = 106. Следовательно, баллон не разрушится.
Па < p * = 106. Следовательно, баллон не разрушится.


