П 1. Система состоит из n блоков. Вероятность безотказной работы блоков в течение времени t: p1(t), p2(t),... pn(t). Блоки отказывают независимо друг от друга. При отказе любого блока система становится неработоспособной. Определить вероятность безотказной работы системы в течение времени t.
Р 1. Отказы любого из n блоков системы являются событиями независимыми, поэтому на основании теории умножения вероятностей независимых событий вероятность безотказной работы системы в течение времени t равна:
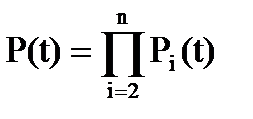 .
.
П 2. Система состоит из основного Б1 и резервного блока Б2 блоков с переключающим устройством П.
Вероятность безотказной работы каждого из блоков в течение времени t равна p(t). При выходе из строя основного блока Б1 происходит мгновенное переключение на резервный Б2. Вероятность безотказной работы переключающего устройства в течение времени t равна 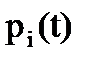 .Определить вероятность безотказной работы системы в течение времени t.
.Определить вероятность безотказной работы системы в течение времени t.
Р 2. Рассмотрим независимые события:
А -отказ блока Б1 в течение времени t, вероятность этого события –1-p(t);
В -отказ резервного блока Б2 вместе в переключателем П.
вероятность события В: (1-p(t)×p1(t)), где p(t)×p1(t) – вероятность безотказной работы резервного блока вместе с переключателем;
С - отказ как основного, так и резервного блока вместе с переключателем. Вероятность этого события: (1-p(t))(1-p1(t)×p(t)).
Событие С- это отказ системы, т.е. Q(t) = (1-p(t))(1-p1(t) × p(t)), поэтому вероятность безотказной работы системы в течение времени t:
P(t) = 1 – Q(t).
ЗАМЕЧАНИЕ: В дальнейшем в постановках задач и пояснениях к решению вместо p(t) –вероятности безотказной работы в течение времени t будем использовать сокращенную запись Р; величину Р будем называть просто надежностью, понимая под этой величиной вероятность безотказной работы в течение определенного времени t.
П 3. Система состоит из основного блока и (n-1) резервных блоков. Каждый резервный блок имеет переключающее устройство подключения очередного резервного блока при отказе работающего блока. Вероятность безотказной работы блока равна Р, вероятность безотказной работы переключающегося устройства p1. Определить вероятность безотказной работы системы.
Р 3. По аналогии с задачей П 2, применяя формулу умножения вероятностей независимых событий, имеем:
s вероятность отказа основного блока – (1-p);
s вероятность отказа одной резервной цепи - (1-pp1);
s вероятность отказа (n-1) резервных цепей - (1-pp1) n-1;
s вероятность отказа основного блока и всех резервных цепей –Q=(1-p)(1-pp1)n-1.
Вероятность безотказной работы системы:
P = 1-Q = 1-(1-p)(1-pp1)n-1 .
П 4. Система состоит из пяти последовательно включенных блоков. К первому, второму и пятому основным блокам постоянно подключены резервные блоки, как показано на рис. Надежности блоков указаны на рис.
Определить надежность Р системы.
Р 4.Отказ любого резервированного блока может произойти только в том случае, если откажет основной блок и все резервные. Поэтому вероятности отказов первого, второго и пятого блоков равны соответственно: (1-p1)2, (1-p2)3, (1-p5)2.
Вероятность безотказной работы всей системы равна произведению вероятностей безотказной работы всех пяти блоков, т.е.:
Р = (1-(1-p1)2)·(1-(1-p2)3)· p3·p4·(1-(1-p5)2).
П 5.Техническое устройство состоит из трех блоков. В первом блоке n1 элементов, во втором n2, в третьем n3.Устройство нормально работает, если исправен Ι блок и хотя бы один из блоков ΙΙ или ΙΙΙ(рис.3). Вероятность безотказной работы элементов одна и та же и равна Р. Отказ элемента в любом из блоков приводит к отказу всего блока. Элементы выходят из строя независимо друг от друга. Определить надежность устройства Р.
Р 3. Надежность блока I: Р1= Рn1;
Надежность блока II: Р2 = Рn2;
Надежность блока III:Р3 = Рn3.
Надежность резервированных блоков II и III:1-(1 - pn2) (1 - pn3 )
Надежность устройства:
Р = pn1 [ 1 – (1 – pn2)(1 – pn3) ].
П 6. На железнодорожную станцию прибыл поезд из К вагонов. Вероятности того, что при движении поезда по перегону в вагонах появится неисправности q1, q2,..., qk. На станции вагоны осматриваются, при наличии неисправности она выявляется, оперативно устраняется с вероятностью p и с вероятностью q = 1- p вагон объявляется исправным. Определить вероятность того, что после осмотра вагонов хотя бы один вагон будет неисправным.
Р 6. Вероятность неисправного состояния i - го вагона после осмотра равна вероятности того, что этот вагон стал неисправным при движении по перегону qi, умноженной на вероятность того, что при осмотре эта неисправность не будет обнаружена q (т.е. неисправность есть, но при осмотре она не выявлена и вагон объявляется исправным). Поэтому (1-qi q) – это вероятность того, что неисправность i- го вагона будет обнаружена и устранена.
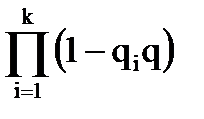
- вероятность того, что во всех К вагонах при наличии в них
неисправностей эти неисправности будут обнаружены и устранены, поэтому вероятность противоположного события, когда хотя бы один вагон после осмотра окажется неисправным, равна:
P = 1 - 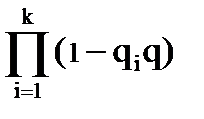 .
.
П 7. Для условий задачи П 6 введено дополнительное условие: после прибытия поезда на станцию с вероятностью Q вагоны поезда не осматриваются и поезд отправляется без осмотра по новому перегону. Определить вероятность того, что при движении поезда по новому перегону хотя бы один вагон окажется неисправным.
Р 7. Неисправность хотя бы одного вагона на новом перегоне возможна при появлении одного из альтернативных событий:
А- вагоны на станции осматривались (вероятность этого события (1- Q)) и хотя бы один вагон после осмотра оказался неисправным (вероятность этого события (1- 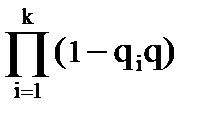 );
);
В- вагоны не осматривались (вероятность этого события Q) и хотя бы один вагон будет неисправен во время движения поезда на перегоне (вероятность этого события (1 - 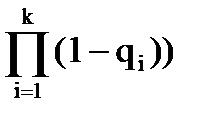 )
)
Искомая вероятность - это вероятность суммы несовместных событий А и В, т.е.:
P = (1-Q) 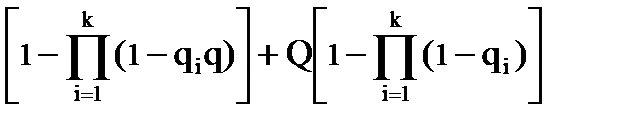 .
.
Расчет надежности устройств по формуле полной вероятности
П 8. Тяговая подстанция работает в двух режимах:
· нормальном;
· в режиме повышенной нагрузки.
В нормальном режиме подстанция работает 80% времени t и 20% времени t в режиме повышенной нагрузки. Вероятность выхода из строя подстанции за время t при работе в нормальном режиме равна 0,1, при работе в режиме перегрузки – 0,7. Определить полную вероятность выхода из строя подстанции за время t.
Р 8. Событие А– выход из строя подстанции за время t может произойти при появлении одного из двух альтернативных событий (гипотез).
Н1 – подстанция работает в нормальном режиме, вероятность такого события Р(Н1) = 0,8;
Н2 – подстанция работает в режиме перегрузки, вероятность этого события Р(Н2) = 0,2.
Вероятность события А по формуле полной вероятности:
Р(А) = Р(Н1) · Р(А/Н1) + Р(Н2) · Р(А/Н2).
Подставляя в эту формулу значения соответствующих вероятностей имеем:
Р(А)= 0,8 ·0,1 + 0,2 · 0,7 = 0,22.
П 9. В автопарке внедряется новая система контроля качества технического обслуживания и ремонта. Система включает в себя два поста предварительного контроля и выходной пост контроля. Автомобиль после ремонта может иметь дефект с вероятностью Р.
После ремонта автомобиль с равной вероятностью проверяется одним из постов предварительного контроля, при этом первый пост предварительного контроля обнаруживает дефект с вероятностью Р1, а второй пост с вероятностью Р2. Если на постах предварительного контроля дефект не обнаруживается, то автомобиль поступает на выходной пост контроля, где дефект, если он имеется, обнаруживается с вероятностью Р0.
В процессе испытаний новой системы контроля в отремонтированном автомобиле был обнаружен дефект.
Определить вероятности того, что дефект был обнаружен:
· первым постом контроля;
· вторым постом контроля;
· выходным постом контроля.
Р 9. До начала контроля автомобиля возможны четыре варианта развития событий:
· Но - дефект в локомотиве не будет обнаружен;
· Н1 - дефект обнаружен первым постом предварительного контроля;
· Н2 - дефект обнаружен вторым постом предварительного контроля;
· Н3 - дефект обнаружен выходным постом контроля.
Рассмотрим событие А- в автомобиле системой контроля обнаружен дефект.
По условию задачи необходимо определить вероятности Р(Нi/A), т.е.вероятности события А при реализации одной из гипотез Но, Н1, Н2, Н3. Очевидно, вероятность события А при реализации гипотезы Но равна нулю, т.е. Р (Н0(A) = 0, поэтому гипотезу Но не рассматриваем.
В соответствии с теоремой умножения вероятностей можно записать:
P(A)× P(Hi /A) = P (Hi) × P(A/ Hi ),
т.е. произведение вероятности события А на условную вероятность гипотезы Hi, при которой появится событие А, равно произведению вероятности гипотезы Hi на условную вероятность события А, которое появится при реализации гипотезы Hi . Из этого выражения имеем:
Р (Hi /A) = 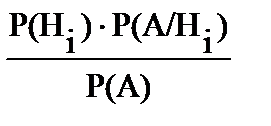 .
.
Вероятность Р(А) можно выразить в виде формулы полной вероятности:
P(A) = 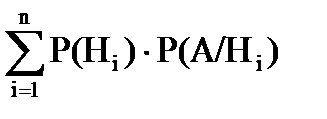 .
.
В результате для определения искомых вероятностей Р(Н1/А), Р(Н2/A), Р(Н3/A) имеем формулу, которая известна как формула Байеса:
Р (Hi /A) = 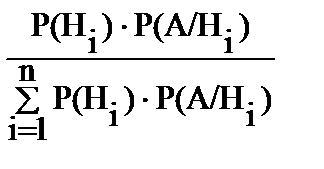 .
.
При реализации одной из гипотез Н1, Н2, Н3 событие А непременно происходит, поэтому условные вероятности Р(А/ H1) = 1, Р(А/ H2) = 1, Р(А/ H3) = 1 и, следовательно, из формулы Байеса имеем:
Р (H1 /A) = 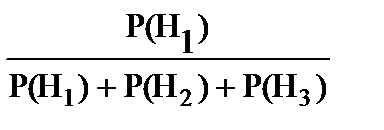 ;
;
Р (H2 /A) = 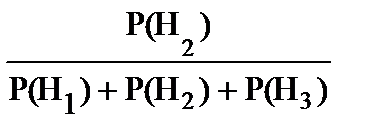 ;
;
Р (H3 /A) = 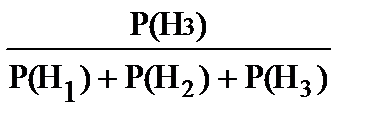 .
.
Определим значения Р (H1), Р (H2), Р (H3).
Для реализации гипотезы Н1 необходимо чтобы:
· автомобиль имел дефект, вероятность этого события равна р;
· автомобиль поступил для контроля на первый пост предварительного контроля, вероятность этого события равна 0,5;
· на первом посту контроля дефект обнаружен, вероятность этого события равна Р1.
В результате по теореме умножения вероятностей:
Р (H1) = 0,5·p·p1.
Аналогично вероятность реализации гипотезы Н2:
Р (H2) = 0,5·p·p2.
Для реализации гипотезы Н3 необходимо совпадение трех событий:
· на пункты контроля поступил автомобиль с дефектом, вероятность этого события равна р;
· дефект автомобиля не обнаружен на первых двух пунктах предварительного контроля, вероятность такого события равна: 1-(0,5Р1+ 0,5 Р2);
· дефект обнаружен выходным постом контроля, вероятность такого события равна Р0.
В результате вероятность реализации гипотезы Н3 будет равна:
P(Н3) = р (1- (0,5 р1+0,5 р2))· ро.
Подставляя полученные выражения в систему уравнений, получим формулы для вычисления искомых вероятностей Р(Н1/A), Р(Н2/A), Р(Н3/A).
Задачи для самостоятельного решения
Задание 1. При испытаниях на надежность группы невосстанавливаемых изделий время испытаний разбито на четыре периода. Установлено, что вероятность отказа в период Т1 составила 0,15, в период Т2- 0,45, в период Т3 - 0,30, в период Т4 =0,1. Найдите вероятность того, что наугад взятое изделие из группы отказало:
либо в первый, либо в третий периоды времени;
либо во второй или третий периоды испытаний.
Задание 2. По статистике, из всех работ по ТО двигателей легковых автомобилей, поступающих на СТОА, 75 % приходится на систему зажигания, 25 % - на систему питания. Какова вероятность того, что очередной автомобиль, поступивший на СТОА для ТО двигателя, будет требовать проведения работ по ТО обеих систем, либо только в системе зажигания или питания?
Задание 3. Система состоит из трех последовательно соединенных изделий, имеющих параметр потока отказов:
α1= 7∙10-3, α 2 = 2∙10-3, α 3 = 1∙10-3.
Определить показатели безотказности системы: среднюю наработку до отказа и вероятность безотказной работы для наработки 50 часов, а также установить, во сколько раз изменится надежность системы при повышении надежности каждого элемента вдвое.
Задание 4. В стенде для диагностики и контроля систем автомобиля для регистрации параметров используются параллельно соединенные аналоговый и цифровой измерительные приборы. Вероятность безотказной работы аналогового прибора при эксплуатации в течение наработки t составляет 0,98, цифрового - 0,99. Определите надежность регистрации параметров на стенде.
Задание 5. Определите показатели безотказности невосстанавливаемого изделия при наработке 1000 часов, если известно, что наработка изделия подчиняется нормальному закону со средней наработкой до отказа 2000 часов и средним квадратическим отклонением наработок s = 500 часов.





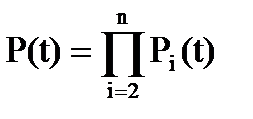 .
.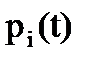 .Определить вероятность безотказной работы системы в течение времени t.
.Определить вероятность безотказной работы системы в течение времени t.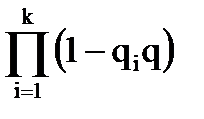
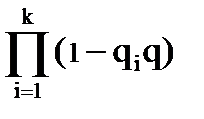 .
.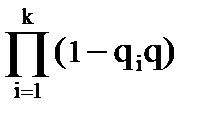 );
); 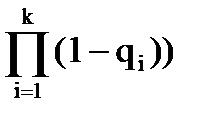 )
)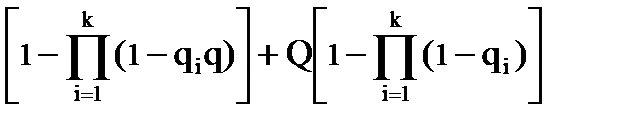 .
.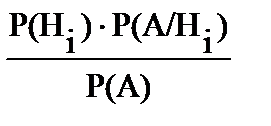 .
.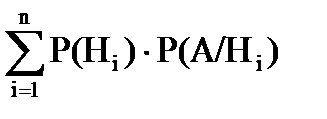 .
.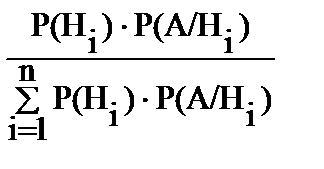 .
.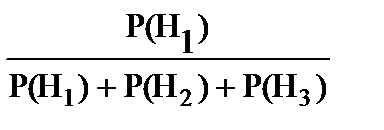 ;
;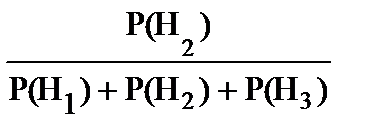 ;
;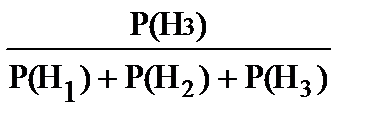 .
.


