Ускорение любой точки плоской фигуры в данный момент времени можно найти, если известны: 1) векторы скорости 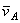 и ускорения
и ускорения 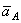 какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фигуры. В ряде случаев вместо траектории второй точки фигуры достаточно знать положение мгновенного центра скоростей.
какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фигуры. В ряде случаев вместо траектории второй точки фигуры достаточно знать положение мгновенного центра скоростей.
Тело (или механизм) при решении задач надо изображать в том положении, для которого требуется определить ускорение соответствующей точки. Расчет начинается с определения по данным задачи скорости и ускорения точки, принимаемой за полюс.
План решения (если заданы скорость и ускорение одной точки плоской фигуры и направления скорости и ускорения другой точки фигуры):
1) Находим мгновенный центр скоростей, восставляя перпендикуляры к скоростям двух точек плоской фигуры.
2) Определяем мгновенную угловую скорость фигуры.
3) Определяем центростремительное ускорение точки вокруг полюса, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.
4) Находим модуль вращательного ускорения, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.
5) Определяем мгновенное угловое ускорение плоской фигуры по найденному вращательному ускорению.
6) Находим ускорение точки плоской фигуры при помощи формулы распределения ускорений.
При решении задач можно применять «теорему о проекциях векторов ускорений двух точек абсолютно твердого тела»:
«Проекции векторов ускорений двух точек абсолютно твердого тела, которое совершает плоскопараллельное движение, на прямую, повернутую относительно прямой, проходящей через эти две точки, в плоскости движения этого тела на угол 
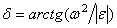 в сторону углового ускорения, равны».
в сторону углового ускорения, равны».
Эту теорему удобно применять, если известны ускорения только двух точек абсолютно твердого тела как по модулю, так и по направлению, известны только направления векторов ускорений других точек этого тела (геометрические размеры тела не известны), не известны  и
и  – соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела.
– соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела.
Известны еще 3 способа определения ускорений точек плоской фигуры:
1) Способ основан на дифференцировании дважды по времени законов плоскопараллельного движения абсолютно твердого тела.
2) Способ основан на использовании мгновенного центра ускорений абсолютно твердого тела (о мгновенном центре ускорений абсолютно твердого тела будет рассказано ниже).
3) Способ основан на использовании плана ускорений абсолютно твердого тела.
Пример. Диск катится без скольжения по прямой. Центр его С имеет скорость 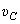 и ускорение
и ускорение  (рис. 43). Найдем ускорение точки А.
(рис. 43). Найдем ускорение точки А.
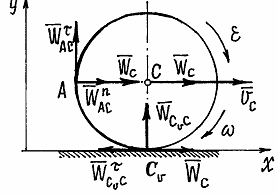
Рис.43
Угловую скорость находим с помощью мгновенного центра скоростей:
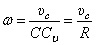 .
.
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что 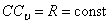 , а точка С движется по прямой, получим
, а точка С движется по прямой, получим
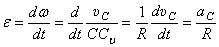 .
.
Если С – полюс, то 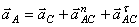 , где
, где
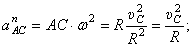
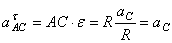 .
.
Величину ускорения найдём с помощью проекций на оси х и у:

Тогда 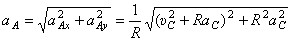 .
.
Ускорение мгновенного центра скоростей  :
:  ,
,
где  .
.
И, так как  , ускорение
, ускорение  и
и  .
.
Таким образом, ускорение мгновенного центра скоростей не равно нулю.
Пример. (рис. 44).
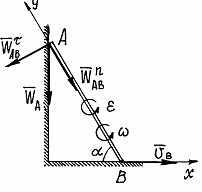
Рис.44
Найдём ускорение точки А, полагая  т.е.
т.е. 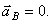
Имеем:
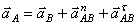 , (1)
, (1)
где  , но направление вектора
, но направление вектора 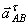 неизвестно, неизвестно и угловое ускорение
неизвестно, неизвестно и угловое ускорение  .
.
Предположим, что вектор 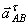 направлен перпендикулярно АВ, влево.
направлен перпендикулярно АВ, влево.
Ускорение 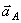 , конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
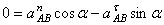 и
и  .
.
Из второго уравнения сразу находим ускорение точки А
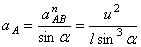 .
.
Положительное значение  указывает на то, что направление вектора
указывает на то, что направление вектора 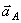 выбрано правильно.
выбрано правильно.
Из первого уравнения можно найти ускорение 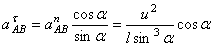 и угловое ускорение
и угловое ускорение 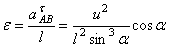 (направления
(направления 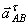 и
и  также угаданы верно).
также угаданы верно).
Мгновенный центр ускорений
При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение 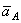 какой-нибудь точки А фигуры и величины
какой-нибудь точки А фигуры и величины  и
и 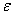 , следующим путем:
, следующим путем:
1) находим значение угла 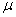 , из формулы
, из формулы 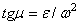 ;
;
2) от точки А под углом 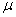 , к вектору
, к вектору 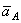 проводим прямую АЕ (рис.45);
проводим прямую АЕ (рис.45);
при этом прямая АЕ должна быть отклонена от 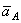 в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения
в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения 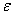 ;
;
3) откладываем вдоль линии АЕ отрезок AQ, равный
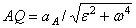 .
.
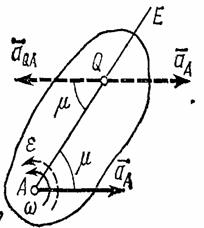
Рис.45
Построенная таким путем точка Q и будет мгновенным центром ускорений. В самом деле, известно что
 ,
,
где численно 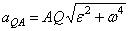 . Подставляя сюда значение AQ находим, что
. Подставляя сюда значение AQ находим, что 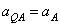 . Кроме того, вектор
. Кроме того, вектор 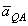 должен образовывать с линией AQ угол
должен образовывать с линией AQ угол 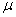 , следовательно, вектор
, следовательно, вектор 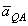 параллелен
параллелен 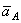 , но направлен в противоположную сторону. Поэтому
, но направлен в противоположную сторону. Поэтому 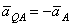 и
и 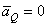 .
.
Если точку Q выбрать за полюс, то так как  , ускорение любой точки М тела, будет
, ускорение любой точки М тела, будет
 .
.
При этом численно
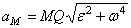 .
.
Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом
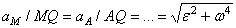 ,
,
т.е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгновенного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.46.
Следует иметь в виду, что положения мгновенного центра скоростей Р и мгновенного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.47), причем скорость его центра С постоянна ( ), то мгновенный центр скоростей находится в точке Р (
), то мгновенный центр скоростей находится в точке Р (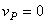 ), но при этом, как было показано
), но при этом, как было показано 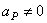 ; следовательно, точка Р не является одновременно мгновенным центром ускорений.
; следовательно, точка Р не является одновременно мгновенным центром ускорений.
Рис.46 Рис.47
Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она движется равномерно и прямолинейно и 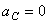 . Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.
. Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.
Понятием о мгновенном центре ускорений удобно пользоваться при решении некоторых задач.
Пример. Плоский механизм, положение которого определяется углами α, β, γ, φ, θ, состоит из стержней, длины которых равны соответственно l1=0.4м, l2=1.2м, l3=1.6м, l4=0.6м. Для заданных значений ω1 и  ε1 найти линейные скорости узловых точек механизма, положения мгновенных центров скоростей звеньев, угловые скорости звеньев, ускорения точек А и В, а также угловое ускорение звена АВ. Схемы механизмов приведены на рис. 6.11. Примечания. Дуговые стрелки на рисунках показывают как при построении чертежа механизма должны откладываться соответствующие углы. Заданные угловые скорости и угловые ускорения считать направленными против хода часовой стрелки. Исходные данные приведены в таблице 6.1.
ε1 найти линейные скорости узловых точек механизма, положения мгновенных центров скоростей звеньев, угловые скорости звеньев, ускорения точек А и В, а также угловое ускорение звена АВ. Схемы механизмов приведены на рис. 6.11. Примечания. Дуговые стрелки на рисунках показывают как при построении чертежа механизма должны откладываться соответствующие углы. Заданные угловые скорости и угловые ускорения считать направленными против хода часовой стрелки. Исходные данные приведены в таблице 6.1.
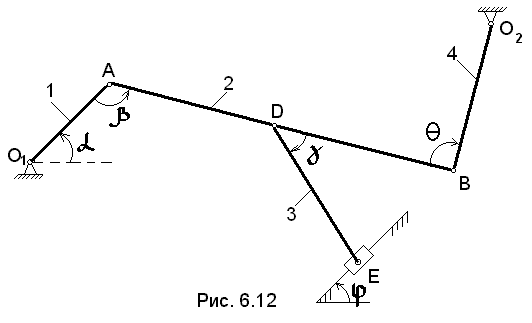
Механизм, см. рис. 6.12, состоит из стержней 1, 2, 3, 4 и ползуна Е, соединенных между собой и с неподвижными опорами О1 и О2 шарнирами. Определить 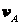 ,
, 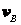 ,
, 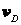 ,
, 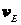 ,
, 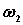 ,
, 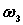 ,
,  ,
, 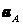 ,
, 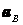 ,
, 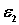 и положение мгновенных центров скоростей звеньев, если дано:
и положение мгновенных центров скоростей звеньев, если дано:
α=0, β=600, γ=300, φ=0, θ=1200, ω1=6с-1, ε1=10с-2, l1=0.4м, l2=1.2м, l3=1.6м, l4=0.6м.
Решение
Согласно условию задачи вычерчиваем механизм в заданном положении (рис. 6.12). Исходя из направления ω1, находим направления скоростей точек А, В, Е (показано на чертеже). Восстанавливаем перпендикуляры к скоростям 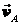 и
и 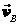 в точках А и В находим положение мгновенного центра скоростей звена АВ – точка Р2. Соединив точку D с Р2 и восстановив перпендикуляр к Р2D в точке D, находим направление скорости
в точках А и В находим положение мгновенного центра скоростей звена АВ – точка Р2. Соединив точку D с Р2 и восстановив перпендикуляр к Р2D в точке D, находим направление скорости 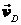 . В точке пересечения перпендикуляров к
. В точке пересечения перпендикуляров к
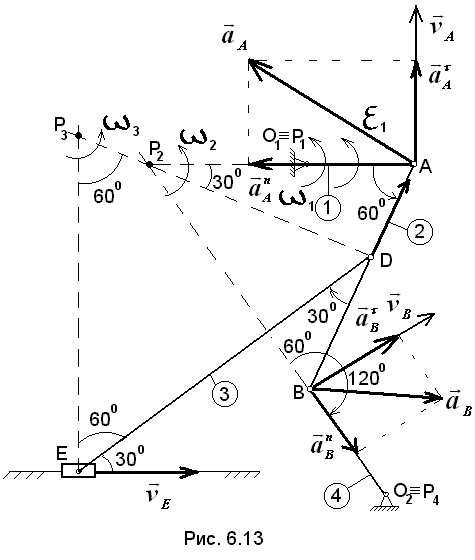
скоростям 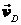 и
и  находится мгновенный центр скоростей звена DE – точка Р3. Находим теперь линейные скорости точек А, В, D, Е и угловые скорости звеньев ω2, ω3, ω4. Имеем
находится мгновенный центр скоростей звена DE – точка Р3. Находим теперь линейные скорости точек А, В, D, Е и угловые скорости звеньев ω2, ω3, ω4. Имеем
 м/с.
м/с.
Так как точка А принадлежит и звену 2, то
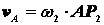
Из равностороннего треугольника АР2В следует, что АР2=ВР2=АВ, следовательно АР2=ВР2=l2=1.2 м. Тогда
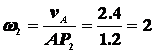 с-1.
с-1.
Значит 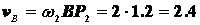 м/с,
м/с,
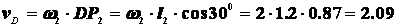 м/с.
м/с.
Однако точка В принадлежит и звену ВО2, поэтому
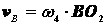 ,
,
откуда 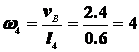 с-1.
с-1.
Точка D принадлежит также звену DE, поэтому
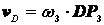
Из равностороннего треугольника DP3E следует, что
DP3=EP3=DE=l3=1.6 м.
Следовательно 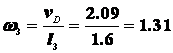 с-1, поэтому линейная скорость точки Е будет
с-1, поэтому линейная скорость точки Е будет 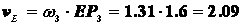 м/с.
м/с.
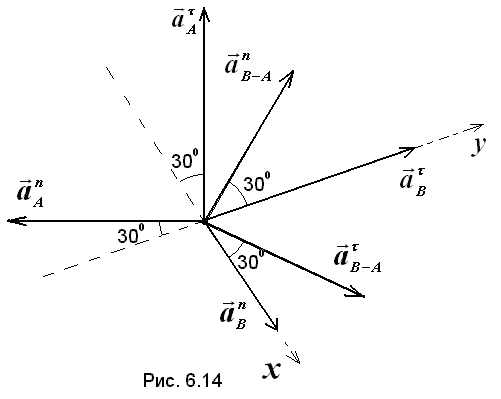
Найдем ускорения точек А и В и угловое ускорение звена АВ. Учитывая, что ускорение точки А равно 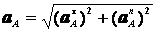
Где 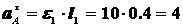 м/с2,
м/с2,
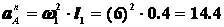 м/с2,
м/с2,
значит 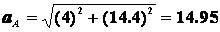 м/с2. Для определения ускорения точки В используем закон распределения ускорений.
м/с2. Для определения ускорения точки В используем закон распределения ускорений.
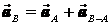 ,
,
или 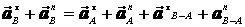 ,
,
где
 , направлено перпендикулярно к О2В,
, направлено перпендикулярно к О2В,
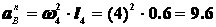 м/с2, направлено от В к О2,
м/с2, направлено от В к О2,
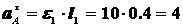 м/с2, направлено перпендикулярно к О1А,
м/с2, направлено перпендикулярно к О1А,
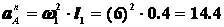 м/с2, направлено от А к О1,
м/с2, направлено от А к О1,  , направлено перпендикулярно к АВ,
, направлено перпендикулярно к АВ,
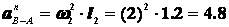 м/с2, направлено от В к А.
м/с2, направлено от В к А.
Направление векторов показано на рис. 6.14. Используя метод проекций находим 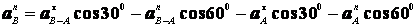 ,
,
откуда
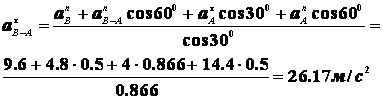
Значит 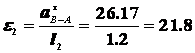 с-2.
с-2.
Проецируя на ось «У» определяем

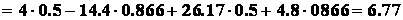 м/с2
м/с2
Тогда полное ускорение точки В определяется
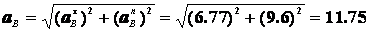 м/с2
м/с2
Ответ: 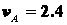 м/с;
м/с; 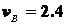 м/с;
м/с; 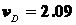 м/с;
м/с; 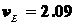 м/с;
м/с;  с-1;
с-1; 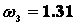 с-1;
с-1; 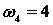 с-1;
с-1; 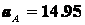 м/с2;
м/с2; 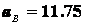 м/с2;
м/с2; 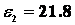 с-2.
с-2.

Таблица 6.1
| № вар
| № схемы
| Углы, град
| ω1
1/c
| ε1
1/c2
|
| α
| β
| γ
| φ
| θ
|
| 1
| 1
| 120
| 30
| 30
| 90
| 150
| 6
| 10
|
| 2
| 2
| 0
| 60
| 90
| 0
| 120
| 4
| 8
|
| 3
| 3
| 60
| 150
| 30
| 90
| 30
| 5
| 6
|
| 4
| 4
| 0
| 150
| 30
| 0
| 60
| 3
| 5
|
| 5
| 5
| 30
| 120
| 120
| 0
| 60
| 2
| 6
|
| 6
| 6
| 90
| 120
| 90
| 90
| 60
| 4
| 8
|
| 7
| 1
| 0
| 150
| 90
| 0
| 120
| 6
| 10
|
| 8
| 2
| 30
| 120
| 30
| 0
| 60
| 7
| 9
|
| 9
| 3
| 90
| 120
| 120
| 90
| 150
| 5
| 8
|
| 10
| 4
| 60
| 60
| 60
| 90
| 30
| 3
| 7
|
| 11
| 5
| 120
| 30
| 30
| 90
| 150
| 2
| 6
|
| 12
| 6
| 0
| 60
| 90
| 0
| 120
| 4
| 5
|
| 13
| 1
| 60
| 150
| 30
| 90
| 30
| 6
| 4
|
| 14
| 2
| 0
| 120
| 30
| 30
| 60
| 3
| 5
|
| 15
| 3
| 30
| 120
| 150
| 30
| 60
| 5
| 6
|
| 16
| 4
| 90
| 150
| 120
| 60
| 150
| 2
| 7
|
| 17
| 5
| 0
| 150
| 90
| 0
| 120
| 3
| 8
|
| 18
| 6
| 30
| 120
| 30
| 0
| 60
| 4
| 9
|
| 19
| 1
| 90
| 120
| 120
| 90
| 150
| 5
| 10
|
| 20
| 2
| 60
| 60
| 60
| 90
| 30
| 6
| 9
|
| 21
| 3
| 120
| 30
| 30
| 90
| 150
| 7
| 8
|
| 22
| 4
| 30
| 60
| 90
| 0
| 120
| 6
| 7
|
| 23
| 5
| 60
| 120
| 30
| 90
| 30
| 5
| 6
|
| 24
| 6
| 30
| 120
| 30
| 30
| 60
| 4
| 5
|
| 25
| 1
| 30
| 120
| 150
| 30
| 60
| 3
| 4
|
| 26
| 2
| 90
| 150
| 120
| 60
| 150
| 2
| 5
|
| 27
| 3
| 0
| 120
| 90
| 30
| 120
| 3
| 6
|
| 28
| 4
| 30
| 120
| 30
| 30
| 60
| 4
| 7
|
| 29
| 5
| 90
| 120
| 120
| 90
| 150
| 5
| 8
|
| 30
| 6
| 60
| 60
| 60
| 90
| 30
| 6
| 9
|





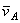 и ускорения
и ускорения 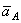 какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фигуры. В ряде случаев вместо траектории второй точки фигуры достаточно знать положение мгновенного центра скоростей.
какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фигуры. В ряде случаев вместо траектории второй точки фигуры достаточно знать положение мгновенного центра скоростей.
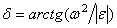 в сторону углового ускорения, равны».
в сторону углового ускорения, равны». и
и  – соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела.
– соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела. 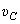 и ускорение
и ускорение  (рис. 43). Найдем ускорение точки А.
(рис. 43). Найдем ускорение точки А.
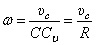 .
.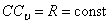 , а точка С движется по прямой, получим
, а точка С движется по прямой, получим 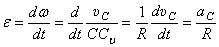 .
.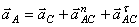 , где
, где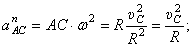
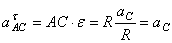 .
.
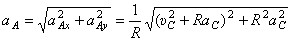 .
. :
:  ,
, .
.  , ускорение
, ускорение  и
и  .
.
 т.е.
т.е. 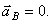
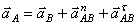 , (1)
, (1) , но направление вектора
, но направление вектора 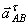 неизвестно, неизвестно и угловое ускорение
неизвестно, неизвестно и угловое ускорение 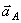 , конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим: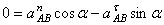 и
и  .
.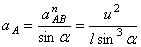 .
. указывает на то, что направление вектора
указывает на то, что направление вектора 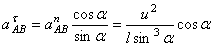 и угловое ускорение
и угловое ускорение 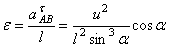 (направления
(направления 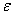 , следующим путем:
, следующим путем: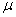 , из формулы
, из формулы 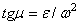 ;
; 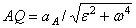 .
.
 ,
,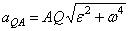 . Подставляя сюда значение AQ находим, что
. Подставляя сюда значение AQ находим, что 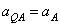 . Кроме того, вектор
. Кроме того, вектор 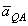 должен образовывать с линией AQ угол
должен образовывать с линией AQ угол 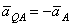 и
и 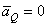 .
.  , ускорение любой точки М тела, будет
, ускорение любой точки М тела, будет .
.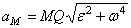 .
.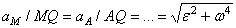 ,
, ), то мгновенный центр скоростей находится в точке Р (
), то мгновенный центр скоростей находится в точке Р (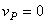 ), но при этом, как было показано
), но при этом, как было показано 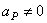 ; следовательно, точка Р не является одновременно мгновенным центром ускорений.
; следовательно, точка Р не является одновременно мгновенным центром ускорений.

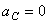 . Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.
. Центры скоростей и ускорений совпадают тогда, когда фигура (тело) вращается вокруг неподвижной оси.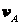 ,
, 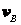 ,
, 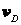 ,
, 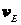 ,
, 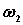 ,
, 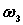 ,
,  ,
, 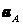 ,
, 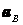 ,
, 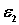 и положение мгновенных центров скоростей звеньев, если дано:
и положение мгновенных центров скоростей звеньев, если дано:
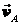 и
и 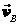 в точках А и В находим положение мгновенного центра скоростей звена АВ – точка Р2. Соединив точку D с Р2 и восстановив перпендикуляр к Р2D в точке D, находим направление скорости
в точках А и В находим положение мгновенного центра скоростей звена АВ – точка Р2. Соединив точку D с Р2 и восстановив перпендикуляр к Р2D в точке D, находим направление скорости 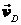 . В точке пересечения перпендикуляров к
. В точке пересечения перпендикуляров к
 находится мгновенный центр скоростей звена DE – точка Р3. Находим теперь линейные скорости точек А, В, D, Е и угловые скорости звеньев ω2, ω3, ω4. Имеем
находится мгновенный центр скоростей звена DE – точка Р3. Находим теперь линейные скорости точек А, В, D, Е и угловые скорости звеньев ω2, ω3, ω4. Имеем м/с.
м/с.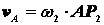
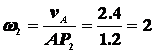 с-1.
с-1.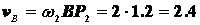 м/с,
м/с,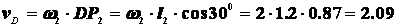 м/с.
м/с.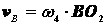 ,
,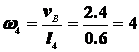 с-1.
с-1.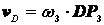
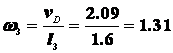 с-1, поэтому линейная скорость точки Е будет
с-1, поэтому линейная скорость точки Е будет 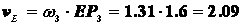 м/с.
м/с.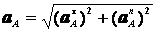
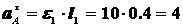 м/с2,
м/с2,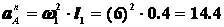 м/с2,
м/с2,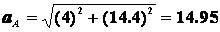 м/с2. Для определения ускорения точки В используем закон распределения ускорений.
м/с2. Для определения ускорения точки В используем закон распределения ускорений.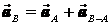 ,
,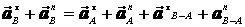 ,
, , направлено перпендикулярно к О2В,
, направлено перпендикулярно к О2В,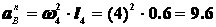 м/с2, направлено от В к О2,
м/с2, направлено от В к О2, , направлено перпендикулярно к АВ,
, направлено перпендикулярно к АВ,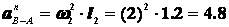 м/с2, направлено от В к А.
м/с2, направлено от В к А.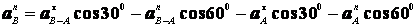 ,
,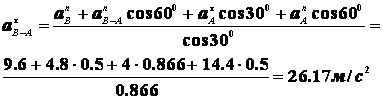
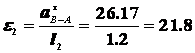 с-2.
с-2.

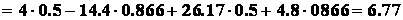 м/с2
м/с2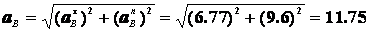 м/с2
м/с2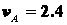 м/с;
м/с; 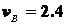 м/с;
м/с; 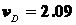 м/с;
м/с; 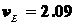 м/с;
м/с;  с-1;
с-1; 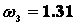 с-1;
с-1; 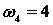 с-1;
с-1; 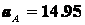 м/с2;
м/с2; 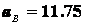 м/с2;
м/с2; 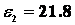 с-2.
с-2.



