ЛОГИКА ПРЕДИКАТОВ. КВАНТОРЫ
Цель работы: научиться читать и строить логические схемы, познакомиться с основами логики предикатов и кванторов.
Логические основы построения ЭВМ
Теоретические сведения
Для описания того, как функционируют аппаратные средства компьютера удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры «1» и «0». Следовательно, одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды в памяти компьютера и в регистрах процессора представляются в виде двоичных последовательностей различной структуры и длины. В логической схеме компьютера выделяют логические элементы.
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарнуюлогическую формулу. Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую формулу, описывающую работу устройств компьютера. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую формулу, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.1.
 Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x. y (читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком " & " (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
 Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис.2. Знак " 1 " на схеме – от устаревшего обозначения дизъюнкции как ">=1" (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис.2. Знак " 1 " на схеме – от устаревшего обозначения дизъюнкции как ">=1" (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
С х е м а НЕ
 Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =  , где читается как "не x" или "инверсия х".
, где читается как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора на рис.3.
С х е м а И–НЕ
 Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:
Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где 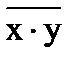 читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И–НЕ с двумя входами представлено на рис.4.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И–НЕ с двумя входами представлено на рис.4.
С х е м а ИЛИ–НЕ
 Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где  читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ–НЕ с двумя входами представлено на рис.5.
читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ–НЕ с двумя входами представлено на рис.5.
Если нужно составить схему по известному логическому выражению, ее начинают строить с конца. Находят операцию, которая будет выполняться последней, и ставят на выходе соответствующий логический элемент. Затем повторяют то же самое для сигналов, поступающих на вход этого элемента. В конце концов должны остаться только исходные сигналы – переменные в логическом выражении.
Примеры решения задач
Пример 1
Составить логическую схему для логического выражения:
F = A Ú B & A.
Две переменные – А и В.
Две логические операции: 1 - &, 2 - Ú.
Строим схему.
Последняя операция – это логическое сложение, поэтому на выходе схемы будет стоять элемент “ИЛИ”.
Добавляем элемент «И» получаем

Пример 2
Дана логическая функция:
F(X,Y) = (X Ú Y) Ú 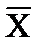 Ù Y
Ù Y
Составить логическую схему для неё.
Решение.
Расставим порядок выполнения логических операций, руководствуясь правилами:
1. Отрицание
2. Умножение
3. Сложение
Не забываем про приоритет скобок. Получаем:
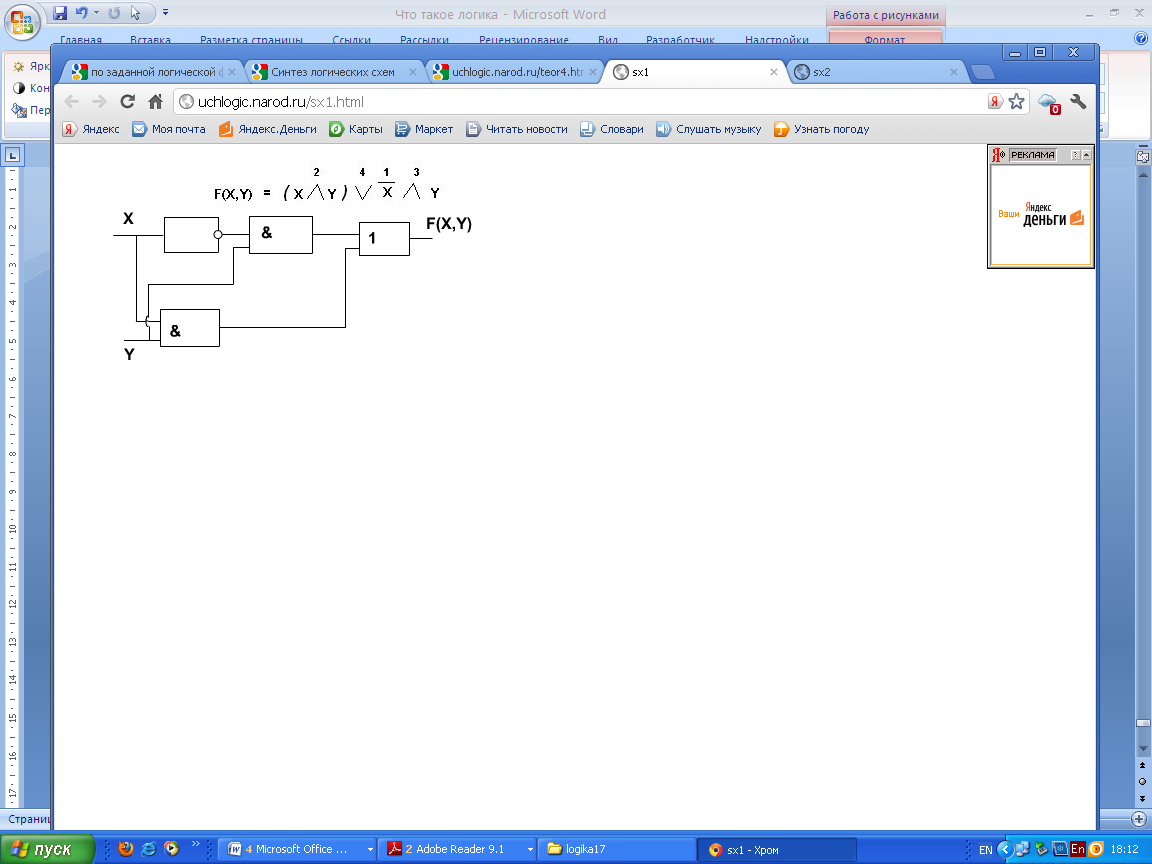
Пример 3
Составить схему, соответствующую выражению

Последняя операция – это логическое сложение, поэтому на выходе схемы будет стоять элемент “ИЛИ”:

Для того чтобы получить на первом входе  ×B, нужно умножить
×B, нужно умножить  на В, поэтому добавляем элемент “И”:
на В, поэтому добавляем элемент “И”:

Чтобы получить  ставим элемент “НЕ”:
ставим элемент “НЕ”:

Аналогично разбираем вторую ветку, которая поступает на второй вход элемента “ИЛИ”:

Пример 4
Построить логическую схему по заданным булевым выражениям.
F =`B A + B`A + C`B.
Построение и расчет схемы осуществляется начиная с ее выхода.
Первый этап: выполняется логическое сложение, логическую операция ИЛИ, считая входными переменными функции `B A, B`A и C`B:

Второй этап: к входам элемента ИЛИ подключаются логические элементы И, входными переменными которых являются уже A, B, C и их инверсии:

Третий этап: для получения инверсий `A и`B на соответствующих входах ставят инверторы:

Данное построение основано на следующей особенности, – поскольку значениями логических функций могут быть только нули и единицы, то любые логические функции могут быть представлены как аргументы других более сложных функций.
Таким образом, построение комбинационной логической схемы осуществляется с выхода ко входу.
Пример 5
Постройте логическую схему, соответствующую логическому выражению F = А & В Ú (В Ú А). Вычислить значения выражения для А = 1, В = 0.
Переменных две: А и В.
Логических операций три: & и две Ú; А & В Ú (В Ú А).
Схему строим слева направо в соответствии с порядком логических операций:

Вычислим значение выражения: F = 1 & 0 Ú (0 Ú 1) = 0
Пример 6
Выписать формулу по заданной функциональной схеме.

Элемент «НЕ» осуществляет логическое отрицание, следовательно на выходе этого элемента  . Элемент “И” осуществляет логическое умножение значений
. Элемент “И” осуществляет логическое умножение значений  и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т. е. вычисляется значение выражения:
и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т. е. вычисляется значение выражения:  .
.
Формула  и есть структурная формула логического устройства.
и есть структурная формула логического устройства.
Выпишем формулу для схемы, изображенной на рис. 1.
 .
.
Пример 7
Выписать формулу по заданной функциональной схеме.

Решение.
Рассматриваем схему с конца и записываем соответствующие логические операции, учитывая, что в записываемой функции три операнда А, В, С

Пример 8
Дана логическая схема:

Построить для неё таблицу истинности.
Решение.
Проверяем количество входов на схеме. Количество комбинаций сигналов на 2 входах равно 4, для 3 входов равно 8, для 4 входов равно 16 и т. д. Составляем таблицу истинности, в которой первые столбцы – это входы схемы, обозначенные буквами, следующие столбцы – функции, полученные на выходах каждого элемента схемы, а строки – отражают разные комбинации сигналов на входах. Количество строк совпадает с количеством комбинаций сигналов. Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах каждого логического элемента, т. е. по каждому столбцу пока не доберёмся до конца схемы. Получаем:

Пример 9
По заданной таблице истинности построить СДНФ, упростить ее и построить функциональную схему.
| X1
| X2
| X3
| F
|
| 0
| 0
| 0
| 1
|
| 0
| 0
| 1
| 1
|
| 0
| 1
| 0
| 0
|
| 0
| 1
| 1
| 0
|
| 1
| 0
| 0
| 0
|
| 1
| 0
| 1
| 0
|
| 1
| 1
| 0
| 0
|
| 1
| 1
| 1
| 1
|
Решение.
1. Выбираем строки, в которых F = 1.
2. Строим для них конъюнкции:
1 строка 
2 строка 
3 строка 
3.Объединяем конъюнкции дизъюнкцией.
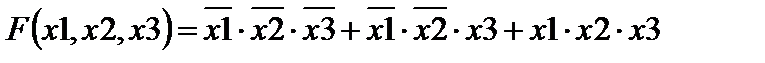
4. Упрощаем логическое выражение.
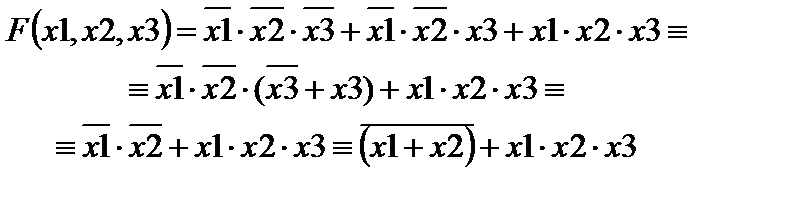
Построим для логического выражения функциональную схему:

Пример 10
Построить СДНФ, упростить формулу и построить схему.
| X1
| X2
| X3
| F
|
| 0
| 0
| 0
| 0
|
| 0
| 0
| 1
| 0
|
| 0
| 1
| 0
| 0
|
| 0
| 1
| 1
| 1
|
| 1
| 0
| 0
| 1
|
| 1
| 0
| 1
| 1
|
| 1
| 1
| 0
| 1
|
| 1
| 1
| 1
| 0
|
Решение
1. Выбираем строки, в которых F = 1, и строим для них минтермы.
4 строка  5 строка
5 строка  6 строка
6 строка 
7 строка 
3. Объединяем минтермы.

3. Упрощаем логическое выражение.

Построим для логического выражения примера функциональную схему:





 Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль. Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис.2. Знак " 1 " на схеме – от устаревшего обозначения дизъюнкции как ">=1" (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис.2. Знак " 1 " на схеме – от устаревшего обозначения дизъюнкции как ">=1" (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y"). Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z =  , где читается как "не x" или "инверсия х".
, где читается как "не x" или "инверсия х". Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:
Схема И–НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где 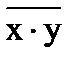 читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И–НЕ с двумя входами представлено на рис.4.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И–НЕ с двумя входами представлено на рис.4. Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом:  , где
, где  читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ–НЕ с двумя входами представлено на рис.5.
читается как "инверсия x или y". Условное обозначение на структурных схемах схемы ИЛИ–НЕ с двумя входами представлено на рис.5.
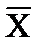 Ù Y
Ù Y


 ×B, нужно умножить
×B, нужно умножить  на В, поэтому добавляем элемент “И”:
на В, поэтому добавляем элемент “И”:




 .
. и есть структурная формула логического устройства.
и есть структурная формула логического устройства. .
.





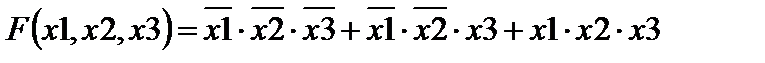
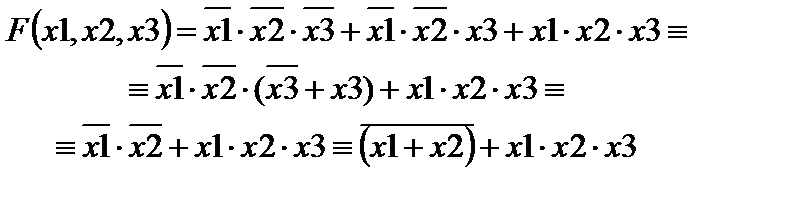

 5 строка
5 строка  6 строка
6 строка 






