1. Отметить те строки таблицы истинности, в последнем столбце которых стоят 1:
| X
| Y
| F(X,Y)
|
| 0
| 0
| 0
|
| 0
| 1
| 1*
|
| 1
| 0
| 1*
|
| 1
| 1
| 0
|
2. Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, то ее отрицание:
 – для 2-й строки;
– для 2-й строки;  – для 3-й строки.
– для 3-й строки.
3. Все полученные конъюнкции связать в дизъюнкцию:
 (1*)
(1*)
Алгоритм получения СКНФ по таблице истинности
1. Отметить те строки таблицы истинности, в последнем столбце которых стоит 0:
| X
| Y
| F(X,Y)
|
| 0
| 0
| 0*
|
| 0
| 1
| 1
|
| 1
| 0
| 1
|
| 1
| 1
| 0*
|
2. Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если равно 1, то ее отрицание:
 — для 1-й строки;
— для 1-й строки;  – для 4-й строки.
– для 4-й строки.
3. Все полученные дизъюнкции связать в конъюнкцию:
 (2*)
(2*)
Если необходимо построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.
Примеры решения задач
Пример 1
По таблице истинности составить логическое уравнение на основе СДНФ (совершенной дизъюнктивной нормальной формы).
Решение:
 Логическая функция СДНФ получается путем составления логической суммы логических произведений, обеспечивающих истинность каждой строки таблицы, где функция истинна (=1).
Логическая функция СДНФ получается путем составления логической суммы логических произведений, обеспечивающих истинность каждой строки таблицы, где функция истинна (=1).
1) Отметить те строки таблицы истинности, в последнем столбце которых стоят 1: это строки 4,6,8
2) Выписать для каждой строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, то ее отрицание:
Для строки 4 это 
Для строки 6 это 
Для строки 8 это 
3) Все полученные конъюнкции связать в дизъюнкцию:

Пример 2
Является ли высказывание (X ® Y) «(Y ® X) тавтологией. Выписать СКНФ и СДНФ.
| X
| Y
| X®Y
| Y®X
| (X®Y)«(Y®X)
|
| 0
| 0
| 1
| 1
| 1
|
| 0
| 1
| 1
| 0
| 0
|
| 1
| 0
| 0
| 1
| 0
|
| 1
| 1
| 1
| 1
| 1
|
Вывод. Высказывание (X®Y)«(Y®X) тавтологией не является, т.к. принимает разные значения.
СДНФ – 
СКНФ — 
Законы логики
Равносильности формул логики высказываний часто называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям.
Перечислим наиболее важные из них:
1. XºX – закон тождества.
2.  – закон противоречия
– закон противоречия
3.  – закон исключенного третьего
– закон исключенного третьего
4.  – закон двойного отрицания
– закон двойного отрицания
5. XÙXºX
– законы идемпотентности
XÚXºC
6. CÙUºUÙC законы коммутативности
CÚUºUÚC (переместительности)
7. (CÙU)ÙZºCÙ(UÙZ) законы ассоциативности
(CÚU)ÚZºCÚ(UÚZ) (сочетательности)
8. CÙ(UÚZ)º(CÙU)Ú(CÙZ) законы дистрибутивности
CÚ(UÙZ)º(CÚU)Ù(CÚZ) (распределительности)
9.  законы де Моргана
законы де Моргана

10. XÙ1ºC CÚ0ºC
11. CÙ0º0; CÚ1º1
12. CÙ(CÚU)ºC
законы поглощения
CÚ(CÙU)ºC
13. (CÚU)Ù( ÚU)ºU
ÚU)ºU
законы склеивания
(CÙU)Ú( ÚU)ºU
ÚU)ºU
14. 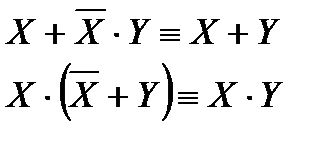

1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. “Это яблоко спелое” и “Это яблоко не спелое”.
Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание.
Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания – то же, что утверждать это высказывание.
“ Неверно, что 2 × 2 ¹ 4”
Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них.
Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел.
В отличие от сложения и умножения чисел логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции.
Доказать законы логики можно:
1) с помощью таблиц истинности;
2) с помощью равносильностей;
3) диаграмм Эйлера-Венна;
4) с помощью логических рассуждений.
Докажем законы склеивания и поглощения с помощью равносильностей:
1) (CÚU)Ù( ÚU)º(C+U)×(
ÚU)º(C+U)×( +U)º
+U)º
ºC×  +U×
+U×  +U×U+C×UºU×
+U×U+C×UºU×  +U+C×UºU×
+U+C×UºU×  +U(1+C)º
+U(1+C)º
ºU×  +UºU(
+UºU( +1)ºU склеивания
+1)ºU склеивания
2) CÙ(CÚU)ºC×CÚC×UºCÚC×UºC(1+U)ºC поглощения
Запишем законы в виде таблицы

Всякую формулу  можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
Любую формулу можно тождественно преобразовать так, что в ней не будут использованы:
· знаки логического сложения;
· знаки логического умножения,
а будут использованы:
· знаки отрицания и логического умножения
· знаки отрицания и логического сложения.
В алгебре логики всякую логическую функцию можно выразить через другие логические функции, но их должно быть по меньшей мере 2 операции, при этом одной из них обязательно должно быть отрицание.
Все операции можно выразить через конъюнкцию и отрицание, дизъюнкцию и отрицание, импликацию и отрицание. Через эквиваленцию и отрицание остальные операции выразить нельзя.
Примеры решения задач
Пример 1
Упростить формулу (А+В)·(А+С)
Решение
а) Раскроем скобки (A+B)·(A+C) º A × A + A × C + B · A + B · C
б) По закону идемпотентности A·AºA, следовательно,
A × A + A × C + B·A + B·C º A + A × C + B·A + B·C
в) В высказываниях А и А·C вынесем за скобки А и используя свойство А + 1 º 1, получим
А + А × С + B × A + B × C º A × (1 + С) + B × A + B × С º A + B × A + B × С
г) Аналогично пункту в) вынесем за скобки высказывание А.
A + B × A + B × С º A (1 + B) + B С º A + B × С
Таким образом, мы доказали закон дистрибутивности.
Пример 2
Упростить выражение А + A × B
Решение. A + A × B º A (1 + B) º A – поглощение
Пример 3
Упростить выражение A×B + A× 
Решение. A × B + A ×  º A (B +
º A (B +  ) º A – склеивание
) º A – склеивание
Пример 4
Преобразовать формулу  так, чтобы не было отрицаний сложных высказываний.
так, чтобы не было отрицаний сложных высказываний.
Решение
1. Воспользуемся формулой де Моргана, получим:


2. Для выражения  применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим:

Пример 5
Преобразовать формулу  так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.
Решение
Воспользуемся законом двойного отрицания, а затем формулой де Моргана.

Пример 6
Преобразовать формулу  так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.
Решение
Используя формулы де Моргана и закон двойного отрицания, получим:

Пример 7
Для какого имени истинно высказывание:
(Первая буква имени гласная -> Четвертая буква имени согласная)?
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Решение. Сложное высказывание состоит из двух простых высказываний:
А – первая буква имени гласная,
В – четвертая буква имени согласная.
(А-> В) = (A V В) = ((А) /\ B) = A /\ B
Применяемые формулы:
1. Импликация через дизъюнкцию А -> В = A V В
2. Закон де Моргана (A V B) = A /\ B
3. Закон двойного отрицания.
(Первая буква имени гласная /\ Четвертая буква имени гласная)
Пример 8
Для какого из указанных значений числа X истинно высказывание
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1))
1) 1 2) 2 3) 3 4) 4
Решение
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1)) – истина, если (X < 5) –> (X < 3) – истина и (X < 2) –> (X < 1) – истина.
Подставляем значения Х:
1) Х = 1
(1 < 5) –> (1 < 3) – истина;
(1 < 2) –> (1 < 1) – ложь, отсюда следует,
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1)) – ложь.
2) Х = 2
(2 < 5) –> (2 < 3) – истина;
(2 < 2) –> (2 < 1) – истина, отсюда следует,
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1)) – истина.
3) Х = 3
(3 < 5) –> (3 < 3) – ложь;
(3 < 2) –> (3 < 1) – истина, отсюда следует,
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1)) – ложь.
4) Х = 4
(4 < 5) –> (4 < 3) – ложь;
(4 < 2) –> (4 < 1) – истина, отсюда следует,
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1)) – ложь.
Ответ: 2
Пример 9
Упростить логическое выражение.
_______________
_____
F = (A v B) → (B v C)
Решение (используются законы де Моргана, закон двойного отрицания, распределительный закон):
_______________ _____
_____ _____
F = (A v B) → (B v C) = A v B & (B v C) = (A v B) & (B v C) = B v (A & C)
Пример 10
Упростите:

Решение

Пример 11
Требуется найти все решения уравнения

Импликация равна нулю только тогда, когда первое выражение равно 1, а второе – 0. Поэтому исходное уравнение сразу разбивается на два

Первое уравнение с помощью закона де Моргана можно преобразовать к виду  откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что A = 1, B = 0 и C = 0 Кроме того, из второго уравнения следует, что D = 0. Решение найдено, причем оно единственное.
откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что A = 1, B = 0 и C = 0 Кроме того, из второго уравнения следует, что D = 0. Решение найдено, причем оно единственное.
Возможен другой вариант – упростить выражение. Заменяя импликацию по формуле  , получаем
, получаем

Используя закон де Моргана

И закон поглощения

Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому A = 1, B = С = D = 0.
Есть и третий вариант – построить таблицу истинности выражения в левой части и найти все варианты, при которых оно равно 0. Однако таблица истинности выражения с четырьмя переменными содержит 24 = 16 строк, поэтому такой подход достаточно трудоемок.
Пример 12
Требуется найти все решения уравнения

Преобразуем выражение, раскрыв импликацию через “НЕ” и “ИЛИ” и применив закон де Моргана:

Если логическая сумма равна 1, то хотя бы одно слагаемое равно 1 (или оба одновременно).
Равенство  верно при A= 0, B= 1 и любых C и D. Поскольку есть всего 4 комбинации значений C и D, уравнение
верно при A= 0, B= 1 и любых C и D. Поскольку есть всего 4 комбинации значений C и D, уравнение  имеет 4 решения:
имеет 4 решения:

Второе уравнение B ⋅ C ⋅ D = 1 дает B = C = D = 1 при любом A, то есть оно имеет два решения:

Видим, что первое из этих решений уже было получено раньше, поэтому уравнение имеет всего пять разных решений. Заметим, что определить все повторяющиеся решения можно из уравнения  , которое
, которое
имеет единственное решение A = 0, B = C = D = 1
Пример 13
Сколько различных решений имеет уравнение
((K Ú L) → (L Ù M Ù N)) = 0
где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение
1) Перепишем уравнение, используя более простые обозначения операций:
((K + L) → (L · M · N)) = 0
2) Из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно
K + L = 1 и L · M · N = 0
3) Из первого уравнения следует, что хотя бы одна из переменных, K или L равна 1 (или обе вместе); поэтому рассмотрим три случая
4) Если K = 1 и L = 0, то второе равенство выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11 ), имеем 4разных решения
5) Если K = 1 и L = 1, то второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3решения
6) Если K = 0, то обязательно L = 1 (из первого уравнения); при этом второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3решения
7) Таким образом, всего получаем 4 + 3 + 3 = 10решений.
Пример 14
Укажите значения переменных К, L, M, N, при которых логическое выражение
((М Ú L) Ù К) → (К Ù М) Ú N)
ложно. Ответ запишите в виде строки из 4 символов: значений переменных К, L, М и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что К = 1, L = 1, M = 0, N = 1.
Решение
1) Запишем уравнение, используя более простые обозначения операций (условие «выражение ложно» означает, что оно равно логическому нулю):

2) Из формулировки условия следует, что выражение должно быть ложно только для одного набора переменных
3) Из таблицы истинности операции «импликация» следует, что это выражение ложно тогда и только тогда, когда одновременно
 и
и 
4) Первое равенство (логическое произведение равно 1) выполняется тогда и только тогда, когда  и
и  ; отсюда следует
; отсюда следует  (логическая сумма равна нулю), что может быть только при
(логическая сумма равна нулю), что может быть только при  ; таким образом, три переменных мы уже определили
; таким образом, три переменных мы уже определили
5) Из второго условия,  , при
, при  и
и  получаем
получаем 
6) Таким образом, правильный ответ – 1000.
Пример 15
По заданной таблице истинности построить СКНФ и упростить ее.
| X1
| X2
| X3
| F
|
| 0
| 0
| 0
| 1
|
| 0
| 0
| 1
| 1
|
| 0
| 1
| 0
| 0
|
| 0
| 1
| 1
| 0
|
| 1
| 0
| 0
| 0
|
| 1
| 0
| 1
| 0
|
| 1
| 1
| 0
| 0
|
| 1
| 1
| 1
| 1
|
Решение
1. Выбираем строки, в которых F=0
2. Выписать для каждой отмеченной строки дизъюнкции:
Если значение некоторой переменной в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если равно 1, то ее отрицание.
3 строка 
4 строка 
5 строка 
6 строка 
7 строка 
3. Объединяем полученные дизъюнкции конъюнкцией.

4. Упрощаем логическое выражение.

Варианты заданий
Вариант 1
1. Составить таблицу истинности для данных операций:

2. Установить, является ли высказывание (X ® Y) « тавтологией.
тавтологией.
3.  Упростить:
Упростить:  ;
;
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
Вариант 2
1. Составить таблицу истинности для данных операций 
2. Установить, является ли высказывание  «
« ) тавтологией.
) тавтологией.
3. Упростить:  ;
;
| X
| Y
| Z
| F
|
| 1
| 0
| 0
| 1
|
| 0
| 0
| 0
| 1
|
| 1
| 1
| 1
| 0
|
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z.
Вариант 3
1. Составить таблицу истинности для данных операций
 (x ~ yz)
(x ~ yz)
2.  Установить, эквивалентны ли высказывания
Установить, эквивалентны ли высказывания



3. Упростить: 
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
Вариант 4
1. Составить таблицу истинности для данных операций  .
.
2. Установить, эквивалентны ли высказывания




3. Данное высказывание преобразовать в эквивалентное, но уже не содержащее отрицаний сложных высказываний: 
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:Какое выражение соответствует F?
1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z.
Вариант 5
1. Составить таблицу истинности для данных операций  ((x ~ z)+ y)
((x ~ z)+ y)
2. Доказать: 
3. Данное высказывание преобразовать в эквивалентное, но уже не содержащее отрицаний сложных высказываний: 
4.  Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z
3) X Ù Y Ù Z 4) X Ù Y Ù Z
Вариант 6
1. Составить таблицу истинности для данных операций  .
.
2. Доказать: 
3.  Упростить:
Упростить: 
4 Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
Вариант 7
1. Составить таблицу истинности для данных операций
((x ~ z)+ y) 
2.  Доказать, является ли данное высказывание тавтологией:
Доказать, является ли данное высказывание тавтологией: 
3. Данное высказывание преобразовать в эквивалентное, но уже не содержащее отрицаний сложных высказываний:

4. Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F?
1) A → (A Ú B) 2) A Ù B 3) A → B 4) A Ù B.
Вариант 8
1. Составить таблицу истинности для данных операций
 .
.
2. Установить, эквивалентны ли высказывания.



3.  Упростить:
Упростить: 
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ù (Y Ú Z) 4) (X Ú Y) Ù Z
Вариант 9
1. Составить таблицу истинности для данных операций  .
.
2. Доказать, является ли данное высказывание тавтологией:

3.  Упростить
Упростить  .
.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ú Y Ù Z 2) X Ú Y Ú Z 3) X Ù Y Ú Z 4) X Ú Y Ù Z.
Вариант 10
1. Составить таблицу истинности для данных операций 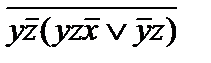 .
.
2. 
Доказать эквивалентность:
3.  Упростить
Упростить  .
.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) (X Ù Y) Ù Z 2) (X Ú Y) Ú Z 3) (X Ù Y) Ú Z 4) (X Ú Y) Ù Z.
Вариант 11
1. Составить таблицу истинности для данных операций
 (z ~ (y + x
(z ~ (y + x  )).
)).
2. Доказать, является ли данное высказывание тавтологией:
 .
.
| X
| Y
| Z
| F
|
| 0
| 0
| 0
| 0
|
| 1
| 0
| 1
| 1
|
| 0
| 1
| 0
| 1
|
3. Упростить  .
.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ù Y Ú Z 4) X Ú Y Ù Z.
 Вариант 12
Вариант 12
1. Составить таблицу истинности для данных операций  .
.
2. Доказать эквивалентность: 
3. Упростить  .
.
4. Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F?
1) A → ((A Ù B)) 2) A Ù B 3) A → B 4) A Ù B.
Вариант 13
1. Составить таблицу истинности для данных операций
 ~ (y + xz))
~ (y + xz))
2. Докажите эквивалентность:

3. Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний: 
4.  Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ú Y Ú Z 3) X Ú Y Ú Z 4) X Ù Y Ù Z.
Вариант 14
1. Составить таблицу истинности для данных операций
 .
.
2. 
Докажите эквивалентность:
3.  Упростить:
Упростить: 
4Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ú Y Ú Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z.
Вариант 15
1. Составить таблицу истинности для данных операций 
2. Докажите, является ли данное высказывание тавтологией:

3.  Упростить
Упростить 
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
1) X Ú Y Ú Z 2) X Ù Y Ù Z
3) X Ù Y Ù Z 4) X Ú Y Ú Z
Контрольные вопросы
1. Что такое логика, формальная логика, математическая логика, алгебра высказываний?
2. Что такое высказывание, виды высказываний. Умозаключение, дедукция?
3. Логические операции. Логические выражения
4. Эквивалентность высказываний.Тавтология.
5. СДНФ и СКНФ.
6. Законы логики.
ЛАБОРАТОРНАЯ РАБОТА №2
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
Цель работы: научиться решать логические задачи различными методами.
Методы решений





 – для 2-й строки;
– для 2-й строки;  – для 3-й строки.
– для 3-й строки. (1*)
(1*) — для 1-й строки;
— для 1-й строки;  – для 4-й строки.
– для 4-й строки. (2*)
(2*) Логическая функция СДНФ получается путем составления логической суммы логических произведений, обеспечивающих истинность каждой строки таблицы, где функция истинна (=1).
Логическая функция СДНФ получается путем составления логической суммы логических произведений, обеспечивающих истинность каждой строки таблицы, где функция истинна (=1).


 – закон противоречия
– закон противоречия – закон исключенного третьего
– закон исключенного третьего – закон двойного отрицания
– закон двойного отрицания законы де Моргана
законы де Моргана
 ÚU)ºU
ÚU)ºU  ÚU)ºU
ÚU)ºU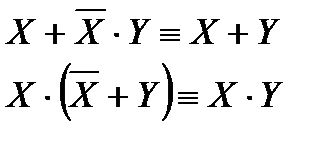


 можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
можно преобразовать так, что в ней не будет отрицаний сложных высказываний – все отрицания будут применяться только к простым высказываниям.
 º A (B +
º A (B +  так, чтобы не было отрицаний сложных высказываний.
так, чтобы не было отрицаний сложных высказываний.

 применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим:
 так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.
 так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.




 откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что A = 1, B = 0 и C = 0 Кроме того, из второго уравнения следует, что D = 0. Решение найдено, причем оно единственное.
откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что A = 1, B = 0 и C = 0 Кроме того, из второго уравнения следует, что D = 0. Решение найдено, причем оно единственное. , получаем
, получаем

 верно при A= 0, B= 1 и любых C и D. Поскольку есть всего 4 комбинации значений C и D, уравнение
верно при A= 0, B= 1 и любых C и D. Поскольку есть всего 4 комбинации значений C и D, уравнение 

 , которое
, которое
 и
и 
 и
и  ; отсюда следует
; отсюда следует  (логическая сумма равна нулю), что может быть только при
(логическая сумма равна нулю), что может быть только при  ; таким образом, три переменных мы уже определили
; таким образом, три переменных мы уже определили получаем
получаем 








 тавтологией.
тавтологией. Упростить:
Упростить:  ;
;
 «
« ) тавтологией.
) тавтологией. ;
; (x ~ yz)
(x ~ yz) Установить, эквивалентны ли высказывания
Установить, эквивалентны ли высказывания



 .
.



 ((x ~ z)+ y)
((x ~ z)+ y)

 Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F? .
.
 Упростить:
Упростить: 

 Доказать, является ли данное высказывание тавтологией:
Доказать, является ли данное высказывание тавтологией: 

 .
.


 Упростить:
Упростить: 
 .
.
 Упростить
Упростить  .
.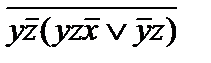 .
.
 Упростить
Упростить  .
. (z ~ (y + x
(z ~ (y + x  )).
)). .
. .
. Вариант 12
Вариант 12 .
.
 .
. ~ (y + xz))
~ (y + xz))

 Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F? .
.
 Упростить:
Упростить: 


 Упростить
Упростить 



