

Инверсия (логическое отрицание) – присоединение частицы «НЕ» к сказуемому данного простого высказывания или присоединение слов «неверно что...» ко всему высказыванию.
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
 Пример. Высказывание А = <Киев – столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т. е. не верно, что <Киев – столица Франции>.
Пример. Высказывание А = <Киев – столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т. е. не верно, что <Киев – столица Франции>.
 Конъюнкция (логическое умножение) – соединение двух высказываний А и В в одно с помощью союза «И».
Конъюнкция (логическое умножение) – соединение двух высказываний А и В в одно с помощью союза «И».
Конъюнкция двух логических высказываний истинна тогда и только тогда, когда оба высказывания истинны.
Пример. Высказывания А = «Москва – столица России» и В = = «Рим – столица Италии». Сложное высказывание А ∧ В (А & В) истинно, так как истинны оба высказывания.
Дизъюнкция (логическое сложение) – соединение двух высказываний А и В в одно с помощью союза «ИЛИ», употребляемого в неисключающем виде.
 Дизъюнкция двух логических высказываний ложна тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция двух логических высказываний ложна тогда и только тогда, когда оба высказывания ложны.
Пример 13. Высказывания А = «2 + + 3 = 5» и В = «3 + 3 = 5». Сложное высказывание: А ∨ В (А + В) истинно, так как истинно высказывание А.
Строгая дизъюнкция ” или «исключающая ИЛИ»
 Этой логической операции соответствует логическая связка “либо... либо”.
Этой логической операции соответствует логическая связка “либо... либо”.
Операция “строгая дизъюнкция” выражается через логические функции “ И ”, “ ИЛИ ”, “ НЕ ” любой из двух логических формул:

и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
 Импликация – логическая операция, соответствующая союзу «если..., то...» Импликация высказываний ложна лишь в случае, когда а истинно, а в ложно.
Импликация – логическая операция, соответствующая союзу «если..., то...» Импликация высказываний ложна лишь в случае, когда а истинно, а в ложно.
Пример. Высказывания А = «2 + 2 = 4» и В = «1 – 8 = 5». Сложное высказывание А → В (А ⇒ В) ложно, так как высказывание А истинно, а В – ложно.
Импликацию можно заменить на выражение, использующее только базовые операции (здесь – только “НЕ” и «ИЛИ»):

Эквиваленция – логическая операция, соответствующая союзу «тогда и только тогда, когда …».
 Эквиваленция двух высказываний истинна в том и только том случае, когда оба эти высказывания истинны или ложны.
Эквиваленция двух высказываний истинна в том и только том случае, когда оба эти высказывания истинны или ложны.
Пример. Высказывания А = «2 + 2 = 7» и В = «1 – 8 = 5». Сложное высказывание А ≡ В (А ~ В) истинно, так как оба высказывания ложны.
Эквивалентность – это обратная операция для “исключающего ИЛИ”, то есть

Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы

 Штрих Шеффера (“И–НЕ”, англ. nand = “not and”)
Штрих Шеффера (“И–НЕ”, англ. nand = “not and”)
Результатом операции антиконъюнкции для высказывания А | В будет ложь только тогда,когда оба высказывания истинны.
Пример. Высказывания А = «Москва – столица России» и В = «Рим – столица Италии». Сложное высказывание А | В ложно, так как истинны оба высказывания.

 C трелка Пирса (“ИЛИ–НЕ”, англ. nor = = “not or”).
C трелка Пирса (“ИЛИ–НЕ”, англ. nor = = “not or”).
Результатом операции антидизъюнкции для высказывания А ↓ В будет истинна только тогда, когда оба высказывания ложны.
Пример. Высказывания А = «Рим – столица России» и В = «Москва – столица Италии».
Сложное высказывание А ↓ В истинно, так как ложны оба высказывания.

Особенность этих операций состоит в том, что с помощью любой одной из них можно записать произвольную логическую операцию. Например, операции “НЕ”, “И” и “ИЛИ” (базовый набор) выражаются через штрих Шеффера так:
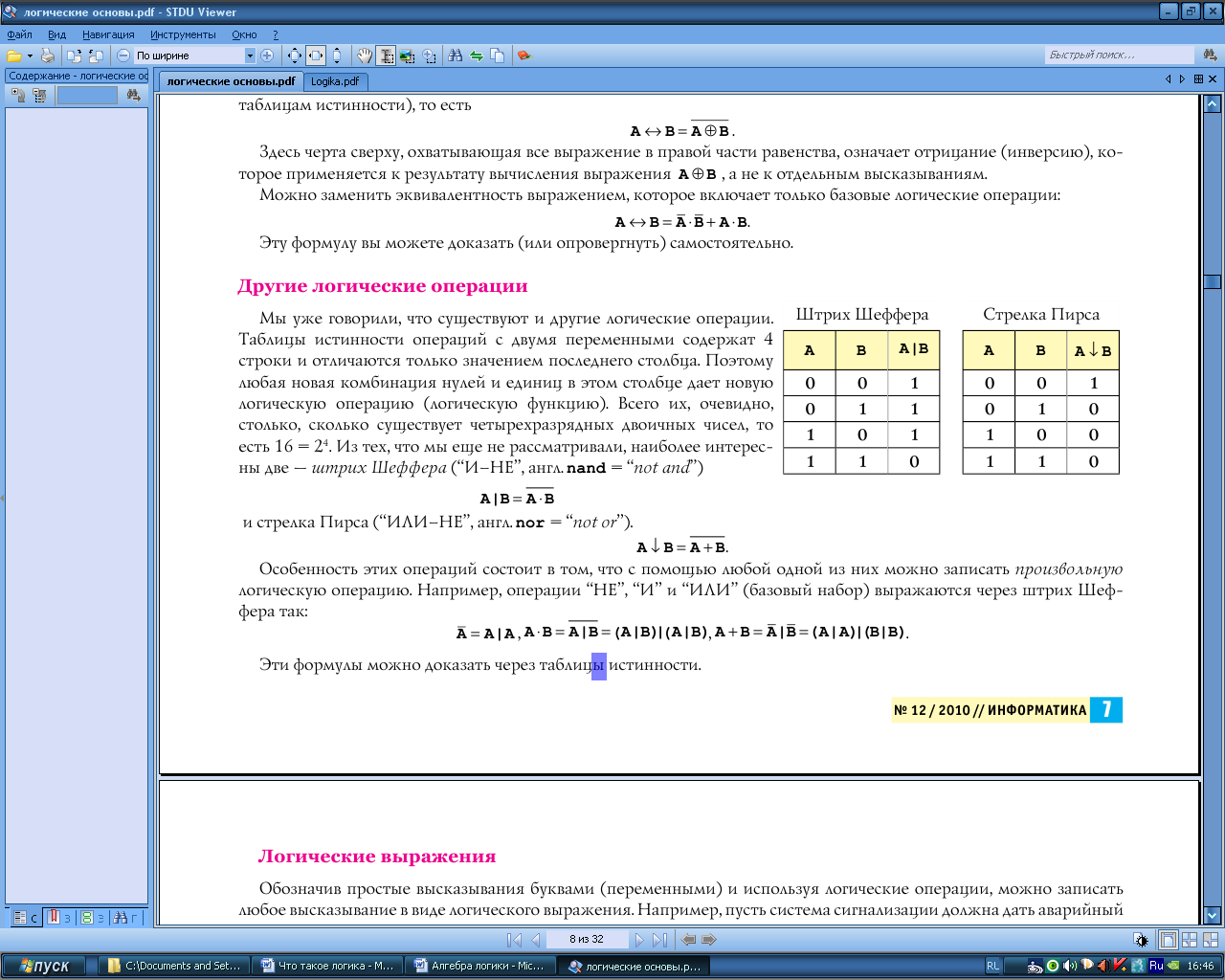
Таблица истинности для основных бинарных логических
Операций

Логические выражения
Обозначив простые высказывания буквами (переменными) и используя логические операции, можно записать любое высказывание в виде логического выражения. Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трех двигателей самолета. Обозначим высказывания:
А – “Первый двигатель вышел из строя”.
B – “Второй двигатель вышел из строя”.
C – “Третий двигатель вышел из строя”.
X – “Аварийная ситуация”.
Тогда логическое высказывание X можно записать в виде формулы
 (*)
(*)
Таким образом, мы выполнили формализацию.
Формализация – это переход от конкретного содержания к формальной записи с помощью некоторого языка.
В логических выражениях операции выполняются в следующем порядке:
Приоритет логических операций:
· действия в скобках;
· инверсия;
· конъюнкция;
· дизъюнкция и исключающая ИЛИ;
· импликация;
· эквивалентность.
Любую формулу можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Сложные выражения удобно разбить на несколько более простых, сначала вычислить значения этих промежуточных величин, а затем – окончательный результат.
Рассмотрим формулу (*). Выражение в правой части зависит от трех переменных, поэтому существует 23 = 8 комбинаций их значений. Таблица истинности выглядит так, как показано выше. По ней видно, что при некоторых значениях переменных значение X истинно, а при некоторых – ложно. Такие выражения называют вычислимыми.
Примеры решения задач
Пример 1
Какие предложения являются высказываниями?
а. 3 + 2 = 5;
б. Не шуметь!
в. y2 ³ 0;
г. Окружностью называется множество всех точек на плоскости, расстояние которых до данной точки этой плоскости имеет заданную величину.
д. Число символов в этом предложении равно 7.
е. 3 < 2;
ж. Войдите!
Ответ: а, д, е.
Пример 2
Среди приведенных ниже высказываний укажите сложные; выделите в них простые, обозначив каждое из них буквой. Запишите с помощью букв каждое сложное высказывание.
а. “На занятии по логики студенты отвечали на вопросы преподавателя и писали самостоятельную работу”.
б. “Мы пойдем кататься на коньках или на лыжах”.
в. “Если в данном четырехугольнике диагонали имеют равную длину, то этот четырехугольник – ромб”.
г. “-17<=0”.
д. “Число 15 делится на 3 тогда и только тогда, когда сумма цифр этого числа делится на 3”.
Ответ:
Сложные высказывания: а), в), д).
а) C: «На занятии по логики студенты отвечали на вопросы преподавателя и писали самостоятельную работу»
D: «Студенты писали самостоятельную работу”.

в) А: «В данном четырехугольнике диагонали имеют равную длину»
В: «Этот четырехугольник – ромб».

д) X: «Число 15 делится на 3»
Y: «Сумма цифр числа 15 делится на 3”.

Пример 3
Даны простые высказывания:
А: “Петя умеет плавать”
В: “Сергей умеет прыгать”
С: “Алеша умеет стрелять”
Даны формулы сложных высказываний, составленные из этих простых. Прочтите их, используя смысл каждого простого высказывания:
1. А+В·  4. А ·
4. А ·  · С
· С
2.  · В·
· В·  5. А·
5. А·  ·
· 
3. А· В·  6.
6. 
Ответ:
1.Алеша не умеет стрелять и Сергей умеет прыгать или Петя умеет плавать.
2. Петя не умеет плавать и Алеша не умеет стрелять и Сергей умеет прыгать.
3. Алеша не умеет стрелять и Петя умеет плавать и Сергей умеет прыгать.
4. Сергей не умеет прыгать и Петя умеет плавать и Алеша умеет стрелять.
5. Алеша не умеет стрелять и Сергей не умеет прыгать и Петя умеет плавать.
6. Неверно что, Петя умеет плавать и Сергей умеет прыгать и Алеша умеет стрелять.
Пример 4
Даны простые высказывания:
- А: “Данное число не кратное 3”
В: “Данное число больше 50”
Прочтите сложные высказывания:
1). А  2).
2).  3).
3).  ·
· 
Ответ:
1.Данное число не больше 50 и данное число не кратное 3.
2. Неверно, что данное число не кратное 3 и данное число больше 50.
3. Данное число кратное 3 и данное число не больше 50.
Пример 5
Прочтите формулы:
а. (A®D) Ù B
б. С Ú А Ù D
в. D Ù (B«( · C))
· C))
Ответ:
а). (A®D) Ù B – В и если А, то Д
б). С Ú А Ù D – A и D или C
в). D Ù (B«( · C)) – D и тогда и только тогда не А и С, когда В.
· C)) – D и тогда и только тогда не А и С, когда В.
Пример 6
Определите значения истинности высказываний:
а. “Если 16 делится на 4, то 16 делится на 2”
б. “Если 17 делится на 4, то 17 делится на 2”
в. “Если 18 делится на 4, то 18 делится на 2”
г. “Если 18 делится на 2, то 18 делится на 4”
д. “Если 2×2=5, то 83 ¹500”
е. “Если 2×2=4, то 72 =81”
ж. “Если телепатия существует, то некоторые физические законы требуют пересмотра”
з. “16 делится на 4 тогда и только тогда, когда 16 делится на 2”
и. “17 делится на 4 тогда и только тогда, когда 17 делится на 2”
к. “18 делится на 4 тогда и только тогда, когда 18 делится на 2”
л. “15 делится на 5 тогда и только тогда, когда 15 делится на 10”
Ответ:
а. истинно;
б. истинно;
в. истинно;
г. ложь;
д. истинно;
е. ложь;
ж. истинно;
з. истинно;
и.
истинно;
к. ложь;
л. ложь.
Пример 7
Каково наибольшее целое число X, при котором истинно высказывание

Сначала удобно заменить импликацию по формуле
А 
Отрицание для высказывания 90 < X 2 запишется как 90 ≥ X2, поэтому 
В этой задаче нас интересуют только целые числа. Поэтому условие 90 ≥ X2 можно заменить на |X| ≤ 9 или −9 ≤ X ≤ 9, а условие 80 > (X + 2)2 – на |X + 2| ≤ 8 или –10 ≤ X ≤ 6. Таким образом, требуется выбрать наибольшее целое число, которое входит в один или в другой промежуток

Это число – 9.
Пример 8
Укажите, какое логическое выражение равносильно выражению
A Ù (B Ú C).
1) A Ú B Ú C 2) A Ú B Ú C 3) A Ù B Ù C 4) A Ù B Ù C.
Решение. Перепишем заданное выражение и ответы в других обозначениях:заданное выражение  ответы: 1)
ответы: 1)  2)
2)  3)
3)  4)
4) 
1) Посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

а затем используем закон двойного отрицания по которому  :
:

2) Таким образом, правильный ответ – 3.
 Пример 9
Пример 9
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
Решение
1) Нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных.
2) Если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F.
3) Перепишем ответы в других обозначениях:
1)  2)
2)  3)
3)  4)
4) 
4) Первое выражение,  , равно 1 только при
, равно 1 только при  , поэтому это неверный ответ (первая строка таблицы не подходит).
, поэтому это неверный ответ (первая строка таблицы не подходит).
5) Второе выражение,  , равно 1 только при
, равно 1 только при  , поэтому это неверный ответ (первая и вторая строки таблицы не подходят).
, поэтому это неверный ответ (первая и вторая строки таблицы не подходят).
6) Третье выражение,  , равно нулю при
, равно нулю при  , поэтому это неверный ответ (вторая строка таблицы не подходит).
, поэтому это неверный ответ (вторая строка таблицы не подходит).
7) Наконец, четвертое выражение,  равно нулю только тогда, когда
равно нулю только тогда, когда 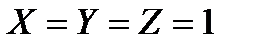 , а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности.
, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности.
Таким образом, правильный ответ – 4.
Пример 10
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| x
| y
| z
| F
|
| 1
| 0
| 0
| 1
|
| 0
| 0
| 0
| 1
|
| 1
| 1
| 1
| 0
|
Какое выражение соответствует F?
1) X /\ Y /\Z 2) X /\ Y /\ Z 3) X \/Y \/ Z 4) X \/ Y \/ Z
Решение:
| x
| y
| z
| x
| y
| z
| F1
| F2
| F3
| F4
| F
|
| 1
| 0
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
| 1
|
| 0
| 0
| 0
| 1
| 1
| 1
| 1
| 0
| 0
| 1
| 1
|
| 1
| 1
| 1
| 0
| 0
| 0
| 0
| 1
| 1
| 0
| 0
|
Из таблицы делаем вывод:
F = X \/ Y \/ Z
Ответ: 4.
Пример 11
Ниже в табличной форме представлен фрагмент базы данных о результатах тестирования учащихся (используется стобалльная шкала)
| Фамилия
| Пол
| Математика
| Русский
язык
| Химия
| Информатика
| Биология
|
| Аганян
| ж
| 82
| 56
| 46
| 32
| 70
|
| Воронин
| м
| 43
| 62
| 45
| 74
| 23
|
| Григорчук
| м
| 54
| 74
| 68
| 75
| 83
|
| Роднина
| ж
| 71
| 63
| 56
| 82
| 79
|
| Сергеенко
| ж
| 33
| 25
| 74
| 38
| 46
|
| Черепанова
| ж
| 18
| 92
| 83
| 28
| 61
|
Сколько записей в данном фрагменте удовлетворяют условию
“Пол=’м’ ИЛИ Химия>Биология”?
1) 5
2) 2
3) 3
4) 4
Решение
Выбираем записи: Мальчики (двое) и Химия>Биология (трое, но один мальчик, уже взялся 1 раз). В итоге 4 записи удовлетворяют условию.
Ответ: 4







 Пример. Высказывание А = <Киев – столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т. е. не верно, что <Киев – столица Франции>.
Пример. Высказывание А = <Киев – столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т. е. не верно, что <Киев – столица Франции>. Конъюнкция (логическое умножение) – соединение двух высказываний А и В в одно с помощью союза «И».
Конъюнкция (логическое умножение) – соединение двух высказываний А и В в одно с помощью союза «И». Дизъюнкция двух логических высказываний ложна тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция двух логических высказываний ложна тогда и только тогда, когда оба высказывания ложны. Этой логической операции соответствует логическая связка “либо... либо”.
Этой логической операции соответствует логическая связка “либо... либо”.
 Импликация – логическая операция, соответствующая союзу «если..., то...» Импликация высказываний ложна лишь в случае, когда а истинно, а в ложно.
Импликация – логическая операция, соответствующая союзу «если..., то...» Импликация высказываний ложна лишь в случае, когда а истинно, а в ложно.
 Эквиваленция двух высказываний истинна в том и только том случае, когда оба эти высказывания истинны или ложны.
Эквиваленция двух высказываний истинна в том и только том случае, когда оба эти высказывания истинны или ложны.

 Штрих Шеффера (“И–НЕ”, англ. nand = “not and”)
Штрих Шеффера (“И–НЕ”, англ. nand = “not and”)



 (*)
(*)



 4. А ·
4. А ·  · С
· С · В·
· В·  5. А·
5. А· 

 3).
3). 



 ответы: 1)
ответы: 1)  2)
2)  3)
3)  4)
4) 

 :
:
 Пример 9
Пример 9 2)
2)  3)
3)  4)
4) 
 , поэтому это неверный ответ (первая строка таблицы не подходит).
, поэтому это неверный ответ (первая строка таблицы не подходит). , поэтому это неверный ответ (первая и вторая строки таблицы не подходят).
, поэтому это неверный ответ (первая и вторая строки таблицы не подходят).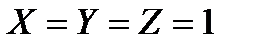 , а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности.
, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности.


