Конструирование (синтез) автоматов – одна из основных задач кибернетики.
(Кибернетика – наука о процессах управления в сложных динамических системах, основывающаяся на теоретическом фундаменте математики и логики, а также применении ВТ.
Автомат – агрегат, представляющий собой систему механизмов и устройств, в которой полностью механизированы, т. е. выполняются без непосредственного участия человека, процессы получения, преобразования, передачи и использования энергии, вещества или информации.)
АЛГОРИТМ СИНТЕЗА АВТОМАТОВ

Примеры решения задач
Пример 1
Для оповещения зрителей, наблюдающих за ходом состязаний по тяжелой атлетике, изготовлен светящийся транспарант: “Вес взят правильно”. Подсвечивание транспаранта осуществляется по команде, выдаваемой автоматом. Этот автомат обрабатывает сигналы, поступающие от трех судей А, В, С. Судья А – старший. Сигнал на подсвечивание транспаранта автомат выдаст тогда, когда нажмут кнопки все трое судей или двое, один из которых – старший. Сконструировать автомат.
Решение
1. Шаг. Описание задачи, которую должен решать автомат принято называть словесной формой задания автомата. Автомат предстает при этом как некий “черный ящик”: еще неизвестно как будет устроен внутри, но уже ясно, что ему предстоит делать, известно как он связан с внешней средой. В данном случае будущий автомат имеет три входа – это линии, по которым поступают сигналы от судей А, В и С и один выход Х (сигнал для подсвечивания транспаранта “вес взят правильно”).
2. Шаг.
3. Шаг. Теперь можно составить таблицу работы автомата.
| А
| В
| С
| Х
|
| 0
| 0
| 0
| 0
|
| 0
| 0
| 1
| 0
|
| 0
| 1
| 0
| 0
|
| 0
| 1
| 1
| 0
|
| 1
| 0
| 0
| 0
|
| 1
| 0
| 0
| 0
|
| 1
| 0
| 1
| 1
|
| 1
| 1
| 0
| 1
|
| 1
| 1
| 1
| 1
|
4. Шаг.
5 Шаг
Пример 2
Три цеха – А, В и С – обеспечивает электроэнергией небольшая электростанция, на которой установлены два генератора – Х и Y. Если в энергии нуждается один из трех цехов, то достаточно включить генератор Y, если же в энергии нуждаются два цеха одновременно достаточно генератора Х. Снабжение обеспечивается совместной работой генераторов X и Y. Необходимо построить такой автомат, который получая заявки от цехов А, В и С на снабжение энергией, может разумно перераспределять нагрузку между генераторами.
Решение
| A
| B
| C
| X
| Y
|
| 0
| 0
| 0
| 0
| 0
|
| 0
| 0
| 1
| 0
| 1
|
| 0
| 1
| 0
| 0
| 1
|
| 0
| 1
| 1
| 1
| 0
|
| 1
| 0
| 0
| 0
| 1
|
| 1
| 0
| 1
| 1
| 0
|
| 1
| 1
| 0
| 1
| 0
|
| 1
| 1
| 1
| 1
| 1
|
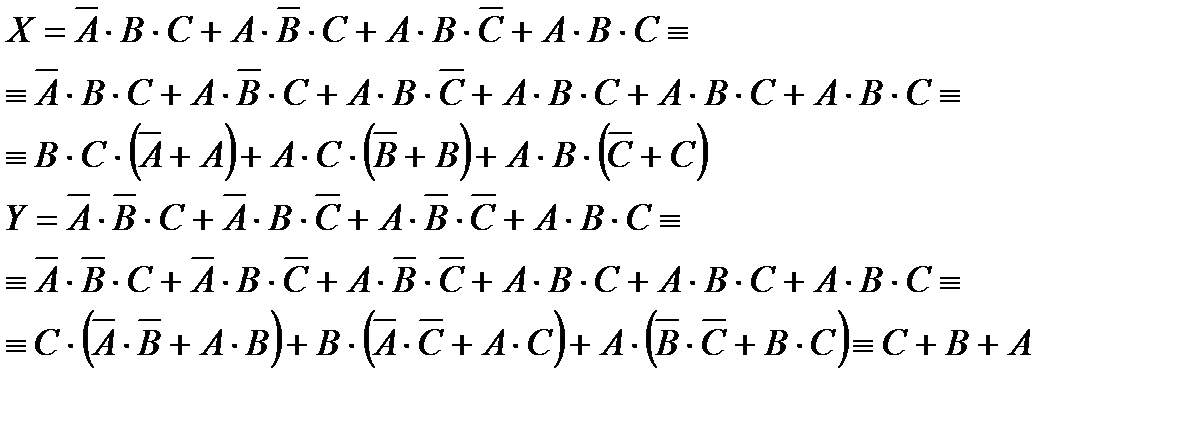
Триггер
Триггер – это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое – двоичному нулю.
В компьютерах триггер используют для запоминания одного бита информации.
Самый распространенный тип триггера – так называемый RS – триггер (S и R соответственно от английских слов set – установка и reset – сброс). Он имеет два симметричных входа S и R и два симметричных выхода Q и  , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала 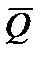 . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.
. На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.
RS-триггер можно построить на двух элементах “И–НЕ” или на двух элементах “ИЛИ–НЕ”. На следующем рисунке показаны условное обозначение RS-триггера, внутреннее устройство триггера на элементах “ИЛИ–НЕ” и его таблица истинности.

Триггер использует так называемые обратные связи – сигналы с выходов схем “ИЛИ–НЕ” поступают на вход соседней схемы. Именно это позволяет хранить информацию. Рассмотрим таблицу истинности триггера. При S = 0 и R = 1. Элемент “ИЛИ–НЕ” в нижней части схемы можно заменить на последовательное соединение элементов “ИЛИ” и “НЕ”. Тогда, независимо от второго входа, на выходе “ИЛИ” будет 1, а на выходе “НЕ” – ноль. Это значит, что Q = 0.
Тогда на входе другого элемента “ИЛИ–НЕ” будут два нуля, а на выходе 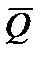 – единица.
– единица.

Поскольку основным выходом считается Q, мы записали в триггер значение 0. Схема симметрична, поэтому при S = 1 и R = 0 в триггере 1 (Q = 1). При S = 0 и R = 0. На выходе первого элемента “ИЛИ” будет сигнал Q + 0 = Q, поэтомна выходе 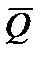 останется его предыдущее значение:
останется его предыдущее значение:

Аналогично легко показать, что на выходе Q тоже остается его предыдущее значение. Это режим хранения бита. Для случая S = 1 и R = 1 оба выхода становятся равны нулю – в этом нет смысла, поэтому такой вариант запрещен.
Для хранения многоразрядных данных триггеры объединяются в единый блок, который называется регистром. Регистры (от 8 до 64 бит) используются во всех процессорах для временного хранения промежуточныхрезультатов.Над регистром, как над единым целым, можно производить ряд стандартных операций: сбрасывать (обнулять), заносить в него код и т. д. Часто регистры способны не просто хранить информацию, но и обрабатывать ее. Триггеры применяются также в микросхемах быстродействующей оперативной памяти.
Сумматор
Сумматор предназначен для сложения (суммирования) двоичных чисел. П олусумматор выполняет сложение двух битов с учетом того, что в результате может получиться двухразрядное число (с переносом в следующий разряд).
 Обозначим через A и B входы полусумматора, а через P и S – выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана на рисунке. Столбец P – это результат операции “И”, а столбец S – результат “исключающего ИЛИ”:
Обозначим через A и B входы полусумматора, а через P и S – выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана на рисунке. Столбец P – это результат операции “И”, а столбец S – результат “исключающего ИЛИ”:

Формулу для S можно также записать в таком виде

что позволяет построить полусумматор, используя всего 4 простейших элемента:

 Слева показано условное обозначение полусумматора, греческая буква Σ здесь (и в математике) обозначает сумму.Полный одноразрядный сумматор учитывает также и третий бит – перенос из предыдущего разряда C. Сумматор имеет три входа и два выхода. Таблица истинности и обозначение сумматора показаны на рисунках.
Слева показано условное обозначение полусумматора, греческая буква Σ здесь (и в математике) обозначает сумму.Полный одноразрядный сумматор учитывает также и третий бит – перенос из предыдущего разряда C. Сумматор имеет три входа и два выхода. Таблица истинности и обозначение сумматора показаны на рисунках.
Сумматор можно построить с помощью двух полусумматоров и одного элемента “ИЛИ”:

Сначала складываются биты B и C, а затем к результату добавляется бит A. Перенос на выходе сумматора появляется тогда, когда любое из двух промежуточных сложений дает перенос.
Для сложения многоразрядных чисел сумматоры объединяют в цепочку. При этом выход P одного сумматора (перенос в следующий разряд) соединяется с входом C следующего. На рисунке показано, как складываются два трехразрядных разрядных числа: X = 1102 и Y = 0112. Сумма Z = 10012 состоит из четырех бит, поэтому на выходе последнего сумматора бит переноса будет равен 1.

Сложение начинается с самого младшего разряда. На вход первого сумматора подаются младшие биты исходных чисел, x1 и y1 (см. рисунок), а на третий вход – ноль (нет переноса из предыдущего разряда). Выход S первого сумматора – это младший бит результата, z1, а его выход P (перенос) передается на вход второго сумматора и т. д. Выход P последнего из сумматоров представляет собой дополнительный разряд суммы, то есть z4. Сумматор играет важную роль не только при сложении чисел, но и при выполнении других арифметических действий. Фактически является основой арифметического устройства современного компьютера.
Понятие предиката
Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно может играть и роль дополнения) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).
Субъект – это то, о чем что-то утверждается в высказывании;
предикат – это то, что утверждается о субъекте.
Например, в высказывании “7 – простое число”, “7” – субъект, “простое число” – предикат. Это высказывание утверждает, что “7” обладает свойством “быть простым числом”.
П еременное высказывание, истинностное значение которого зависит от параметра, и называется предикатом.
Таким образом, предикат есть функция, определенная на некотором множестве параметров и со значениями в {0, 1}.
Определение 1. Одноместным предикатом Р(х) называется такая функция одного переменного, в которой аргумент х пробегает значения из некоторого множества М, а функция при этом принимает одно из двух значений: истина или ложь.
Множество М, на котором задан предикат, называется областью определения предиката.
Определение 2. N -местным предикатом называется такая функция n переменных Q(x1, x2, …,xn), определенная на множестве М=М1´М2´…´Мn и принимающая на этом множестве одно из двух значений: истина или ложь.
Само множество М называется пред метным множеством, а аргументы x1 ,..., xn Î M – предметными переменными.
Множество М, на котором задан предикат, называется областью определения предиката.
Множество 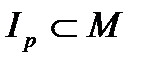 , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).
, на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).
Можно считать, что высказывание это нульместный предикат, то есть предикат, в котором нет переменных для замены.
Например.
Пусть предметное множество М есть класс млекопитающих. Рассмотрим одноместный предикат Р(х): у х четыре ноги. Тогда Р(слон) = 1, Р(кошка) = 1, Р(человек) =0.
Пусть М – множество натуральных чисел. Рассмотрим двухместный предикат G (x, y): х<у. Тогда, например, G(l,3) = l, G(8,5) = 0.
Предикат называется:
А) тождественно истинным, если значение его для любых аргументов есть «истина» (Предикат Р(х) называется тождественно истинным на множестве М, если  )
)
Б) тождественно ложным, если значение его для любых аргументов есть «ложь» (Предикат Р(х) называется тождественно истинным на множестве М, если 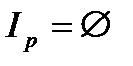 );
);
В) выполнимым, если существует, по крайней мере, одна n-система его аргументов, для которой значение предиката есть «истина».
Например
Предикат “x+y=y+x” является тождественно истинным, предикат “x+1=x” – тождественно ложным, предикат “x+y=5” – выполнимым.
Пример 1. Среди следующих предложений выделите предикаты:
1) Луна есть спутник Венеры
2) Планеты х и y принадлежат Солнечной системе
3) 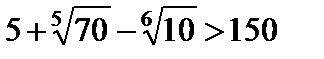
4) 
5) 
6) Любое простое число Р не имеет делителей, отличных от себя и 1
7) Натуральное число n не меньше 1
8) Треугольник АВС равен треугольнику А1В1С1
9) 
10) 
11) 
Ответ: 2), 4) 7)-11).
Пример 2. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности.
1) х+5=1
2) при х=2 выполняется равенство 
3) 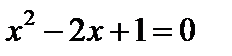
4) существует такое число х, что 
5) x+2<3x-4
6) однозначное число х кратно3;
7) (х+2)-(3х-4).
Решение.
1) Предложение х+5=1 является одноместным предикатом Р(х), Ip={-4}
2) предложение «при х=2 выполняется равенство 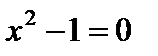 » не является предикатом. Это ложное высказывание.
» не является предикатом. Это ложное высказывание.
3) Предложение  является одноместным предикатом Р(х), Ip={1}
является одноместным предикатом Р(х), Ip={1}
4) предложение «существует такое число х, что  » не является предикатом. Это истинное высказывание.
» не является предикатом. Это истинное высказывание.
5) Предложение «x+2<3x-4» является одноместным предикатом Р(х), Ip=(3;+¥)
6) Предложение «однозначное число х кратно3» является одноместным предикатом Р(х), Ip={0; 3; 6; 9);
7) Предложение «(х+2)-(3х-4)» не является предикатом.





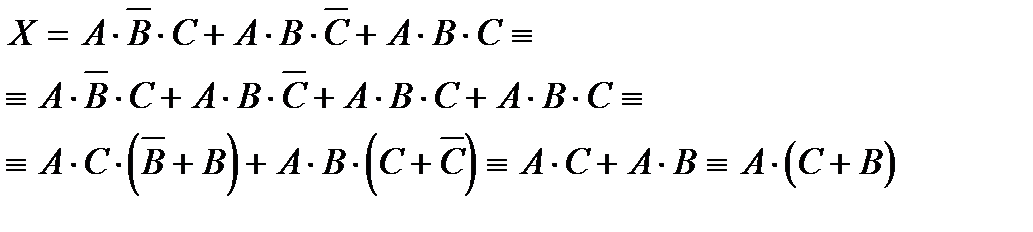
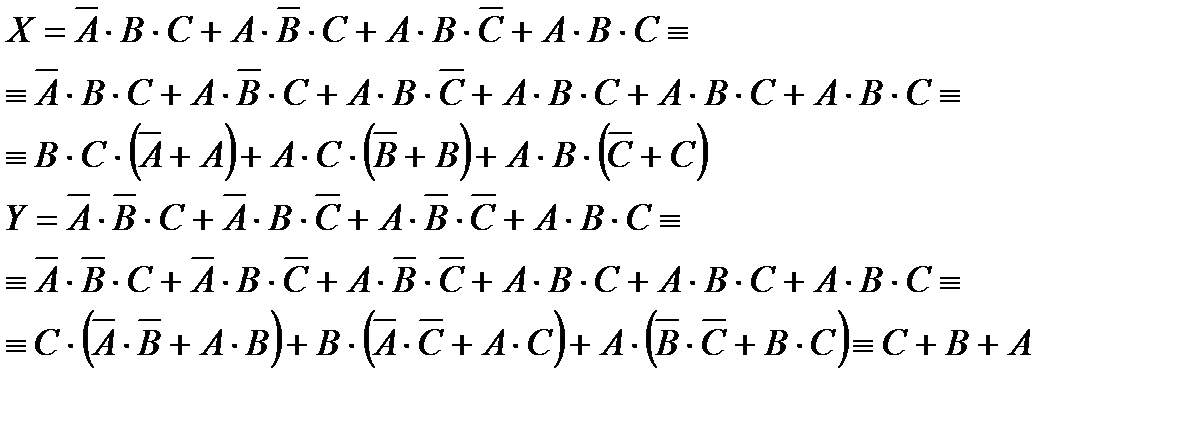
 , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала 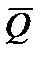 . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.
. На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов. Наличие импульса на входе будем считать единицей, а его отсутствие – нулем.


 Обозначим через A и B входы полусумматора, а через P и S – выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана на рисунке. Столбец P – это результат операции “И”, а столбец S – результат “исключающего ИЛИ”:
Обозначим через A и B входы полусумматора, а через P и S – выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана на рисунке. Столбец P – это результат операции “И”, а столбец S – результат “исключающего ИЛИ”:


 Слева показано условное обозначение полусумматора, греческая буква Σ здесь (и в математике) обозначает сумму.Полный одноразрядный сумматор учитывает также и третий бит – перенос из предыдущего разряда C. Сумматор имеет три входа и два выхода. Таблица истинности и обозначение сумматора показаны на рисунках.
Слева показано условное обозначение полусумматора, греческая буква Σ здесь (и в математике) обозначает сумму.Полный одноразрядный сумматор учитывает также и третий бит – перенос из предыдущего разряда C. Сумматор имеет три входа и два выхода. Таблица истинности и обозначение сумматора показаны на рисунках.

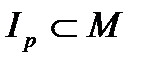 , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).
, на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х). )
)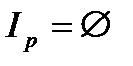 );
);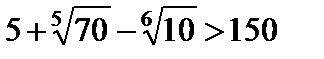






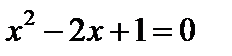

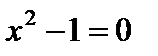 » не является предикатом. Это ложное высказывание.
» не является предикатом. Это ложное высказывание. является одноместным предикатом Р(х), Ip={1}
является одноместным предикатом Р(х), Ip={1} » не является предикатом. Это истинное высказывание.
» не является предикатом. Это истинное высказывание.

