1) Отрицанием предиката P (x) называется новый предикат 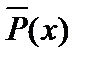 , множество истинности которого является дополнением множества истинности предиката Р (х), то есть
, множество истинности которого является дополнением множества истинности предиката Р (х), то есть 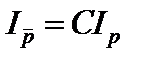 .
.
2) Конъюнкцией предикатов P (x) и Q (x) называется новый предикат 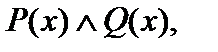 который принимает значение 1 при тех и только тех значениях
который принимает значение 1 при тех и только тех значениях 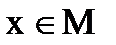 , при которых каждый из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях.
, при которых каждый из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях.
Очевидно, что множество истинности 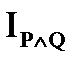 есть пересечение множеств истинности
есть пересечение множеств истинности 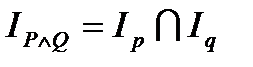
3) Дизъюнкцией предикатов P (x) и Q (x) называется новый предикат 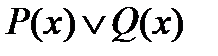 , который принимает значение 1 при тех и только тех значениях
, который принимает значение 1 при тех и только тех значениях 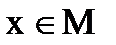 , при которых хотя бы один из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях. Очевидно, что множество истинности
, при которых хотя бы один из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях. Очевидно, что множество истинности 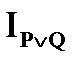 есть объединение множеств истинности
есть объединение множеств истинности 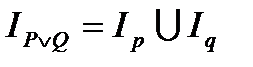
4) Импликацией предикатов P (x) и Q (x) называется предикат 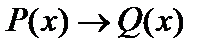 , который имеет значение ложь на тех и только на тех наборах аргументов х, на которых P (x) имеет значение 1, а Q (x) – значение 0. Очевидно, что множество истинности
, который имеет значение ложь на тех и только на тех наборах аргументов х, на которых P (x) имеет значение 1, а Q (x) – значение 0. Очевидно, что множество истинности 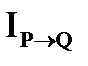 есть объединение множеств истинности
есть объединение множеств истинности 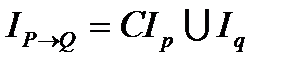
5) Эквиваленцией P (x) и Q (x) называется предикат 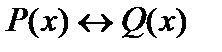 , который имеет значение истина на тех и только на тех наборах аргументов х, на которых значения истинности P (x) и Q (x) совпадают. Очевидно, что множество истинности
, который имеет значение истина на тех и только на тех наборах аргументов х, на которых значения истинности P (x) и Q (x) совпадают. Очевидно, что множество истинности 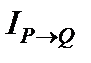 есть объединение множеств истинности
есть объединение множеств истинности 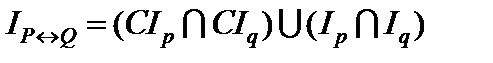
Примеры решения задач
Пример 1. Пусть даны предикаты P ( x ): «х – четное число» и Q ( x ): «х кратно 3», определенные на множестве N. Найти области истинности предикатов:
1)  ; 2)
; 2) 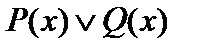 ; 3)
; 3) 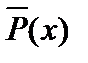 ; 4)
; 4) 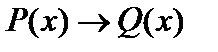
Решение
Т.к. 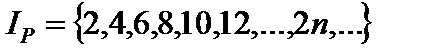 ,
, 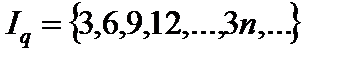
1) 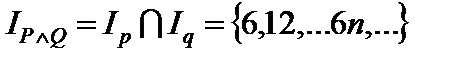
2) 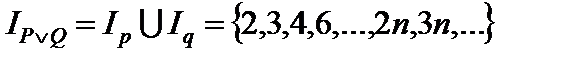
3) 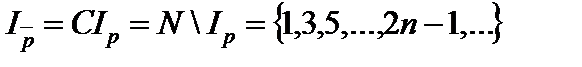
4) 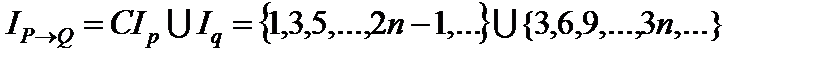
Субъект – в логике подлежащее суждения, то есть предмет, о котором что-либо говорится или мыслится.
Пример 2. Если значения x, y принадлежат отрезку [2;5], то в списке выражений следующего вида:
1) х=2 или y=7
2) x-y
3) x+y<2
4) 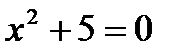
5) 3<x<y<5
6) x>12
Ответ: Число истинных и ложных предикатов соответственно равно 1,5
Пример 3. Множество истинности предиката p (x)=” x + y =0”, где x, y – целые числа принадлежат отрезку [-2;4], равно…
А) {-2,-1,1,2}
Б) {(-2,2), (-1,1)}
В) {(-2,2), (-1,1), (0,0)}
Г) [-2;2]
Д) [-1;1]
Решение
{(-2,2), (-1,1), (0,0)}
Пример 4 Для предиката р(х): ” div (x,3)= mod (x,2)”, где x изменяется на множестве X ={2,3,5,10,19}, область истинности равна
А) {2,3,5,10}
Б) {10,19}
В) {2, 3, 5}
Г) {2, 5, 10}
Д) {5}
Решение.
{5}
Пример 5. Запишите предикат (условие, которое может быть и сложным), полностью описывающий область, нестрого заключенную между окружностью с центром в начале координат и радиусом 2 и квадратом, в который вписана эта окружность.
Решение
Уравнение рассматриваемой окружности имеет вид: 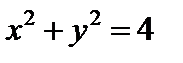 . Уравнения рассматриваемого квадрата –
. Уравнения рассматриваемого квадрата – 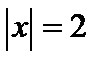 ,
, 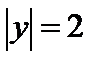 . Искомая область образуется пересечением внешней области окружности, определяемой неравенством
. Искомая область образуется пересечением внешней области окружности, определяемой неравенством 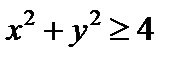 , и внутренней области квадрата, определяемой неравенствами:
, и внутренней области квадрата, определяемой неравенствами: 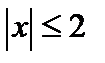 ,
, 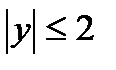 .Нестрогие неравенства означают, что границы окружности и квадрата входят в область, т. е. допустимы равенства.
.Нестрогие неравенства означают, что границы окружности и квадрата входят в область, т. е. допустимы равенства.
Ответ: (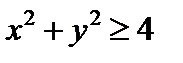 ) и (
) и (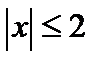 ) и (
) и ( )
)
Кванторы
Квантор логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения.
В обычном языке носителями таких характеристик служат слова типа "все", "каждый", "некоторый", "существует", "имеется", "любой", "всякий", "единственный", "несколько", "бесконечно много", "конечное число", а также все количественные числительные.
Для предикатов вводятся две новые по сравнению с логикой высказываний операции: квантором общ ности и квантором существования.
Квантор общности
Пусть Р(x) – одноместный предикат, определенный на предметном множестве М.
Универсальным высказыванием, соответствующим предикату Р(x), называется высказывание «каждый элемент множества М удовлетворяет предикату Р(x)» (или «для всякого х выполняется предикат»), которое обозначается (" x) P (x).
Высказывание ("x)P(x) считается истинным, если предикат P(x) тождественно истинный, а ложным – в противном случае.
Символ "x называется квантором общности по переменной х, его читают так: «для всех х», или «для каждого х», или «для любого х».
Выражение ("x)P(x) читается: «для всех х, Р(х)», или «для каждого х, Р(х)».
Например, "x(х=х) – это истинное универсальное высказывание, а "x(х>2) – ложное универсальное высказывание.
Если Р(х) - одноместный предикат, определенный на конечном множестве {a1,a2,…am}, то 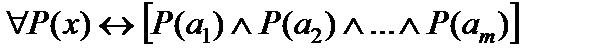
Таким образом, квантор общности можно понимать как оператор конъюнкции по квантифицируемой переменной.
Квантор существования
Экзистенциональным высказыванием, соответствующим предикату Р(x), называется высказывание «существует элемент множества М, удовлетворяющий предикату Р(x)», которое обозначается $x P(x) и считается истинным, если предикат Р(х) выполнимый, а ложным – в противном случае.
Символ $x называют квантором существования, а выражение $x, в котором этот квантор предшествует переменной х, читают так: «существует х такой, что…», или «для некоторого х, …», или «для некоторого х, Р(х)».
Например, $x(х>2) – это истинное экзистенциональное высказывание, а $x(х=х+1) – ложное экзистенциональное высказывание.
Если Р(х) - одноместный предикат, определенный на конечном множестве {a1,a2,…am}, то 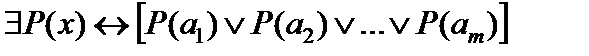
Таким образом, квантор существования можно понимать как оператор дизъюнкции по квантифицируемой переменной.
Операцию навешивания квантора " или квантора $ на переменную х называют еще квантификацией переменной х.
Примеры решения задач
Пример 1. Прочтите следующие записи, заменив обозначения кванторов общности и существования их словесными выражениями:
А) 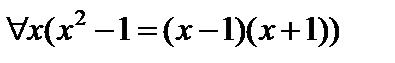
Б) 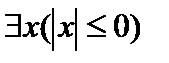
В) 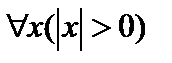
Г) 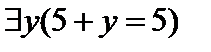
Д) 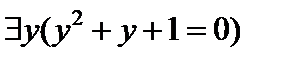
Е) 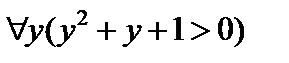
Ж) 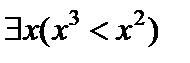
Решение
А) 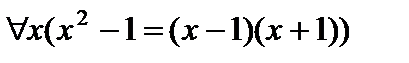 — «Для всех х выполняется предикат
— «Для всех х выполняется предикат 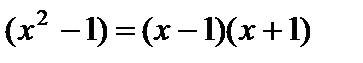 »;
»;
Б) 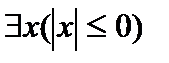 — «Для некоторого х, справедливо
— «Для некоторого х, справедливо 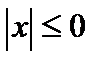 »;
»;
В) 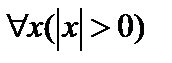 — «Для всех х,
— «Для всех х, 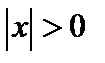 »;
»;
Г) 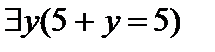 — «Существует y такой, что 5+y=5»;
— «Существует y такой, что 5+y=5»;
Д) 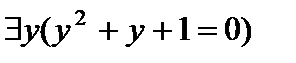 — «Существует y такой, что
— «Существует y такой, что 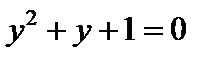 ».
».
Е) 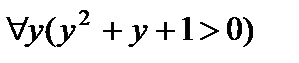 — «Для всех y выполняется предикат
— «Для всех y выполняется предикат 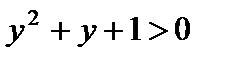 »;
»;
Ж) 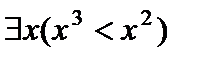 – «Для некоторого х, справедливо
– «Для некоторого х, справедливо 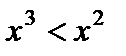 »
»
Пример 2. Запишите следующие предложения, используя символы кванторов:
А) «Существует число х такое, что х+10=2»;
Б) «По крайней мере, одно число y является корнем уравнения 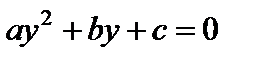 »;
»;
В) «Каково бы ни было число z, z+0=z»;
Г) «Уравнение f(x)=o имеет хотя бы один корень»;
Д) «Любое число либо положительно, либо отрицательно, либо равно нулю».
Решение.
А) $x(х+10=2) – «Существует число х такое, что х+10=2»;
Б) $y(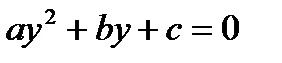 ) – «По крайней мере, одно число y является корнем уравнения
) – «По крайней мере, одно число y является корнем уравнения 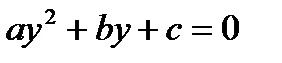 »;
»;
В) "z(z+0=z) – «Каково бы ни было число z, z+0=z»;
Г) $x(f(x)=0) – «Уравнение f(x)=o имеет хотя бы один корень»;
Д) $x(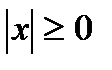 ) – «Любое число либо положительно, либо отрицательно, либо равно нулю».
) – «Любое число либо положительно, либо отрицательно, либо равно нулю».
Формулы логики предикатов
В логике предикатов будем пользоваться следующей символикой:
1. Символы p, q, r, …- переменные высказывания, принимающие два значения: 1- истина, 0 – ложь.
2. Предметные переменные – x, y, z, …, которые пробегают значения из некоторого множества М;
x0, y0, z0 – предметные константы, т. е. значения предметных переменных.
3. P(·), Q(·), F(·), … – одноместные предикатные переменные;
Q(·,·,…,·), R(·,·, …,·) – n-местные предикатные переменные.
P0(·), Q0(·,·, …,·) – символы постоянных предикатов.
4. Символы логических операций: 
5. Символы кванторных операций: 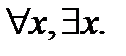
6. Вспомогательные символы: скобки, запятые.
Предметная переменная называется свободной, если она не следует непосредственно за квантором и не входит в область действия квантора по этой переменной, все другие переменные, входящие в формулу, называются связанными.
Формулой логики предика тов являются
a) Каждая предикатная буква и предикатная буква со следующими за ней в скобках предметными переменными;
b) выражения вида FÙ G, F Ú G, Ø G, F Þ G, F ÛG, (" y) F, ($ y) G, где F и G – формулы логики предикатов, переменная у Î М.
Примеры:
· P; Q(x,y,z); R(x1,x2) – элементарные формулы
· 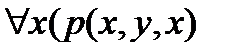 ;
; 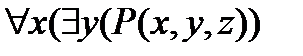 ;
; 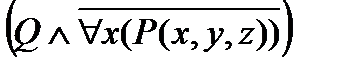 – составные формулы.
– составные формулы.
Примеры решения задач
Пример 1. Дана формула 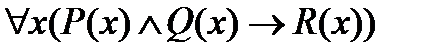 , где предикаты P(x), Q(x), R(x) определены на множестве N. Найти ее значение, если
, где предикаты P(x), Q(x), R(x) определены на множестве N. Найти ее значение, если
a) P (x): «число х делится на 3», Q(x): «число х делится на 4», R (x) «число х делится на 2»;
b) P (x): «число х делится на 3», Q(x): «число х делится на 4», R (x) «число х делится на 5»;
Решение
В обоих случаях конъюнкция  есть утверждение, что число х делится на 12. Но тогда при всех х, если число х делится на 12, то оно делится и на 2, и, значит, в случае 1) формула истинна.Так как из делимости числа х на 12 не при всех х следует делимость числа х на 5, то в случае 2) формула ложна.
есть утверждение, что число х делится на 12. Но тогда при всех х, если число х делится на 12, то оно делится и на 2, и, значит, в случае 1) формула истинна.Так как из делимости числа х на 12 не при всех х следует делимость числа х на 5, то в случае 2) формула ложна.





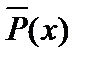 , множество истинности которого является дополнением множества истинности предиката Р (х), то есть
, множество истинности которого является дополнением множества истинности предиката Р (х), то есть 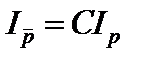 .
.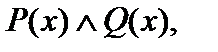 который принимает значение 1 при тех и только тех значениях
который принимает значение 1 при тех и только тех значениях 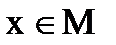 , при которых каждый из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях.
, при которых каждый из предикатов P (x) и Q (x) принимает значение 1 и принимает 0 во всех остальных случаях.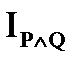 есть пересечение множеств истинности
есть пересечение множеств истинности 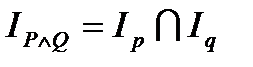
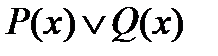 , который принимает значение 1 при тех и только тех значениях
, который принимает значение 1 при тех и только тех значениях 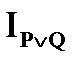 есть объединение множеств истинности
есть объединение множеств истинности 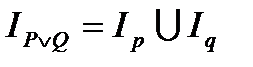
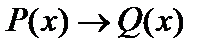 , который имеет значение ложь на тех и только на тех наборах аргументов х, на которых P (x) имеет значение 1, а Q (x) – значение 0. Очевидно, что множество истинности
, который имеет значение ложь на тех и только на тех наборах аргументов х, на которых P (x) имеет значение 1, а Q (x) – значение 0. Очевидно, что множество истинности 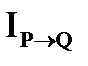 есть объединение множеств истинности
есть объединение множеств истинности 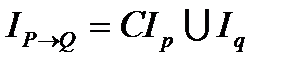
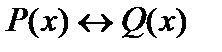 , который имеет значение истина на тех и только на тех наборах аргументов х, на которых значения истинности P (x) и Q (x) совпадают. Очевидно, что множество истинности
, который имеет значение истина на тех и только на тех наборах аргументов х, на которых значения истинности P (x) и Q (x) совпадают. Очевидно, что множество истинности 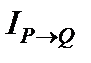 есть объединение множеств истинности
есть объединение множеств истинности 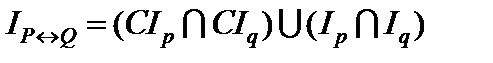
 ; 2)
; 2) 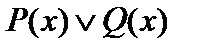 ; 3)
; 3) 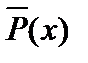 ; 4)
; 4) 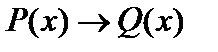
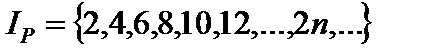 ,
, 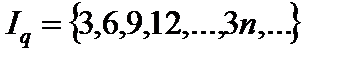
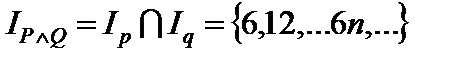
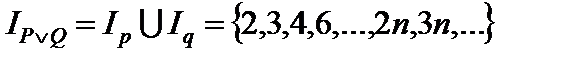
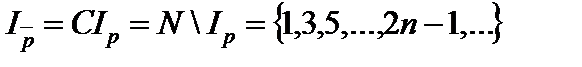
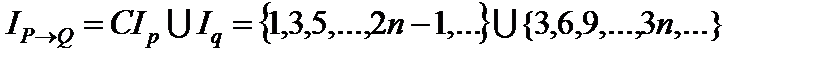
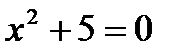
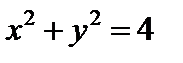 . Уравнения рассматриваемого квадрата –
. Уравнения рассматриваемого квадрата – 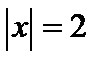 ,
, 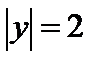 . Искомая область образуется пересечением внешней области окружности, определяемой неравенством
. Искомая область образуется пересечением внешней области окружности, определяемой неравенством 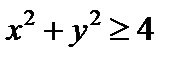 , и внутренней области квадрата, определяемой неравенствами:
, и внутренней области квадрата, определяемой неравенствами: 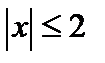 ,
, 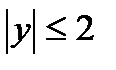 .Нестрогие неравенства означают, что границы окружности и квадрата входят в область, т. е. допустимы равенства.
.Нестрогие неравенства означают, что границы окружности и квадрата входят в область, т. е. допустимы равенства.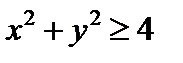 ) и (
) и (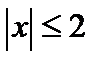 ) и (
) и ( )
)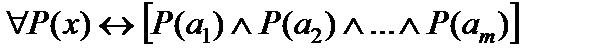
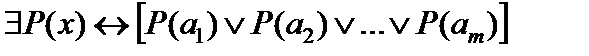
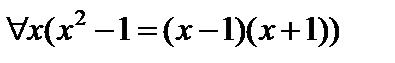
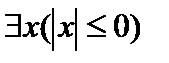
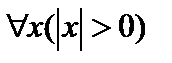
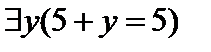
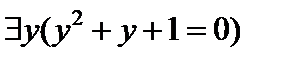
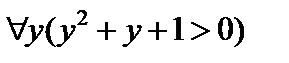
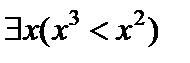
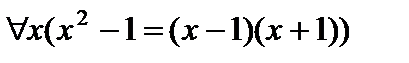 — «Для всех х выполняется предикат
— «Для всех х выполняется предикат 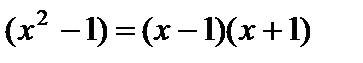 »;
»;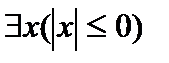 — «Для некоторого х, справедливо
— «Для некоторого х, справедливо 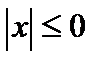 »;
»;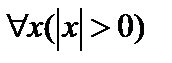 — «Для всех х,
— «Для всех х, 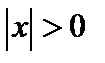 »;
»;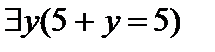 — «Существует y такой, что 5+y=5»;
— «Существует y такой, что 5+y=5»;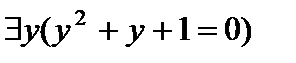 — «Существует y такой, что
— «Существует y такой, что 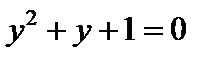 ».
».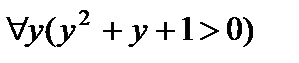 — «Для всех y выполняется предикат
— «Для всех y выполняется предикат 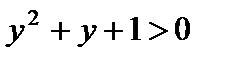 »;
»;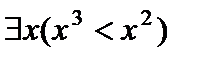 – «Для некоторого х, справедливо
– «Для некоторого х, справедливо 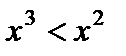 »
»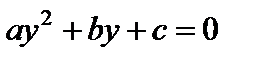 »;
»;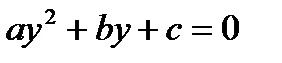 ) – «По крайней мере, одно число y является корнем уравнения
) – «По крайней мере, одно число y является корнем уравнения 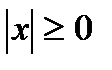 ) – «Любое число либо положительно, либо отрицательно, либо равно нулю».
) – «Любое число либо положительно, либо отрицательно, либо равно нулю».
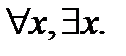
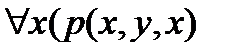 ;
; 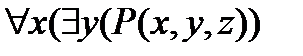 ;
; 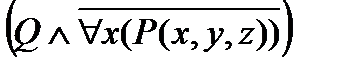 – составные формулы.
– составные формулы.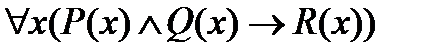 , где предикаты P(x), Q(x), R(x) определены на множестве N. Найти ее значение, если
, где предикаты P(x), Q(x), R(x) определены на множестве N. Найти ее значение, если есть утверждение, что число х делится на 12. Но тогда при всех х, если число х делится на 12, то оно делится и на 2, и, значит, в случае 1) формула истинна.Так как из делимости числа х на 12 не при всех х следует делимость числа х на 5, то в случае 2) формула ложна.
есть утверждение, что число х делится на 12. Но тогда при всех х, если число х делится на 12, то оно делится и на 2, и, значит, в случае 1) формула истинна.Так как из делимости числа х на 12 не при всех х следует делимость числа х на 5, то в случае 2) формула ложна.


