Системы логических уравнений

Примеры решения задач

 

Пример 1

Следующие два высказывания истинны:

(1). Неверно, что если корабль A вышел в море, то корабль C – нет.

(2). В море вышел корабль B или корабль C, но не оба вместе.

Определить, какие корабли вышли в море.

Обозначим буквами высказывания:

A – “корабль A вышел в море”,

B – “корабль B вышел в море”,

C – “корабль C вышел в море”.

Тогда высказывание “ если корабль A вышел в море, то корабль C – нет ”можно записать в виде  Поусловию (1), это высказывание неверно,таким образом,   Крометого, из (2) получаем . Итак,решение задачи сводится к решению системы логических уравнений

 

Нужно найти тройку логических значений A, B и C, при которых оба уравнения превращаются в истинные равенства. Покажем несколько способов решения этой системы.

Способ 1. Сведение к одному уравнению.

Преобразуем уравнения так, чтобы правые части были равны 1 (истинному значению). Для этого применим инверсию (операцию “НЕ”) к обеим частям первого уравнения:

 

 

Теперь представляем импликацию и “исключающее ИЛИ” через базовые операции (“И”, “ИЛИ”,“НЕ”):

 

Поскольку необходимо, чтобы левые части обоих уравнений были равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:

 

 

Раскрываем инверсию в первой скобке по закону де Моргана и вносим “сомножитель” A в скобку, не забыв, что

 

 

Последнее уравнение, равносильное исходной системе, имеет единственное решение: A = 1, B = 0 и C = 1. Таким образом, в море вышли корабли А и C.

Способ 2. Таблица истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. Для системы с тремя переменными возможны 8 вариантов:

 

Зеленым цветом выделена единственная строчка, для которой выполняются условия задачи, то есть   и A ⊕ B = 1. Таким образом, A = 1, B = 0 и C = 1, это значит, что в море вышли корабли А и C. Недостаток этого метода – трудоемкость при большом количестве переменных (больше 4).

Способ 3. Последовательное решение уравнений

В некоторых случаях можно решать уравнения последовательно, на каждом шаге добавляя по одной переменной в рассматриваемый набор. Чтобы вводить переменные в алфавитном порядке, поменяем местами уравнения в нашей системе:

Мы видим, что первое уравнение зависит только от A и B, а в третьем подключается переменная C. Будем строить дерево решений и одновременно записывать его в свернутом виде в таблицу. Переменная A может принимать два значения:

 

 

Из первого уравнения A ⊕ B = 1. следует, что A ≠ B, поэтому при A = 0 получаем единственный вариант B = 1, а при A = 1 имеем B = 0. Итак, первое уравнение имеет два решения относительно переменных A и B.

 

Теперь “подключаем” второе урав­нение A → C = 0, из которого нужно определить допустимые значения C для каждого варианта. При A = 0 импликация не может быть ложна, то есть первая строчка предыдущей таблицы не дает ни одного решения системы двух уравнений. При A = 1 получаем единственное решение, для которого C = 1:

Таким образом, существует единственное решение системы: A = 1, B = 0 и C = 1. Это значит, что в море вышли корабли А и C.

Пример 2

Найти количество решений системы уравнений:

 

,

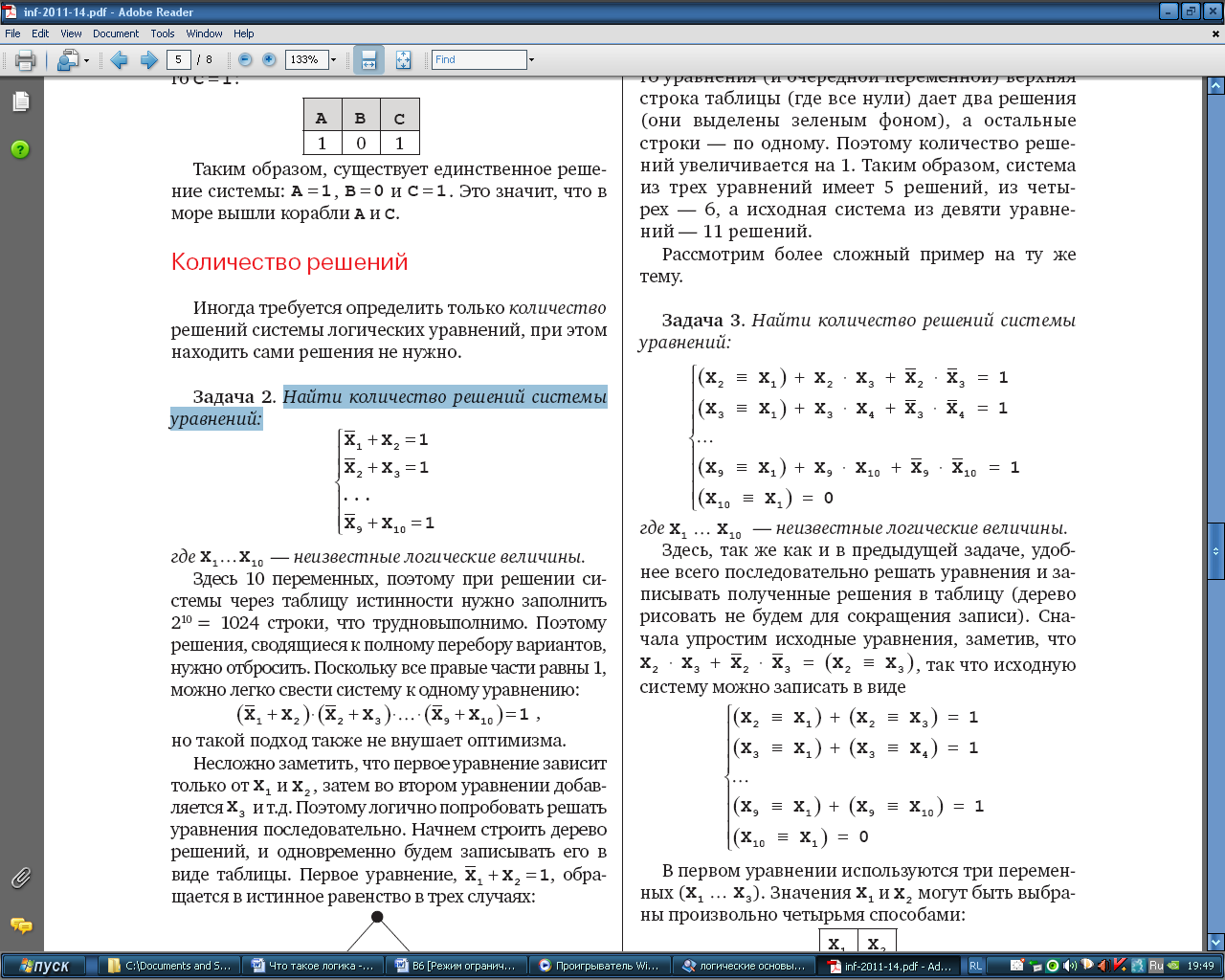где X₁…X₁₀ – неизвестные логические величины.Здесь 10 переменных, поэтому при решении системы через таблицу истинности нужно заполнить2¹⁰ = 1024 строки, что трудно выполнимо. Поэтомурешения, сводящиеся к полному перебору вариантов,нужно отбросить. Первое уравнение зависит только от X₁ и X₂, затем во втором уравнении добавляется X₃ и т. д. Поэтому логично попробовать решать уравнения последовательно. Начнем строить дерево решений, и одновременно будем записывать его в виде таблицы. Первое уравнение,  обращается в истинное равенство в трех случаях:

 

 

Теперь подключаем второе уравнение, + Х ₃ = 1. Допустимые значения X3 зависят от ранее выбранного значения X₂: если X₂ = 0, то X₃ может принимать любое значение (0 или 1), а если X₂ = 1, то X₃ = 1. Дерево и соответствующая ему

 

 

Легко заметить, что при добавлении очередного уравнения (и очередной переменной) верхняя строка таблицы (где все нули) дает два решения (они выделены зеленым фоном), а остальные строки – по одному. Поэтому количество решений увеличивается на 1. Таким образом, система из трех уравнений имеет 5 решений, из четырех – 6, а исходная система из девяти уравнений – 11 решений.

Пример 3

Сколько различных решений имеет система логических уравнений

 

где x _i, y _i, i = – логические переменные

 

Поскольку уравнения системы не зависят друг от друга, их можно решать отдельно. Первое уравнение равносильно системе

 

 

 

которая имеет ровно 6 решений (см. пример):

Второе уравнение также имеет 6 различных решений. В силу независимости уравнений исходной системы общее количество решений равно 36 = 6 × 6.

Пример 4

Сколько различных решений имеет система логических уравнений

 

 

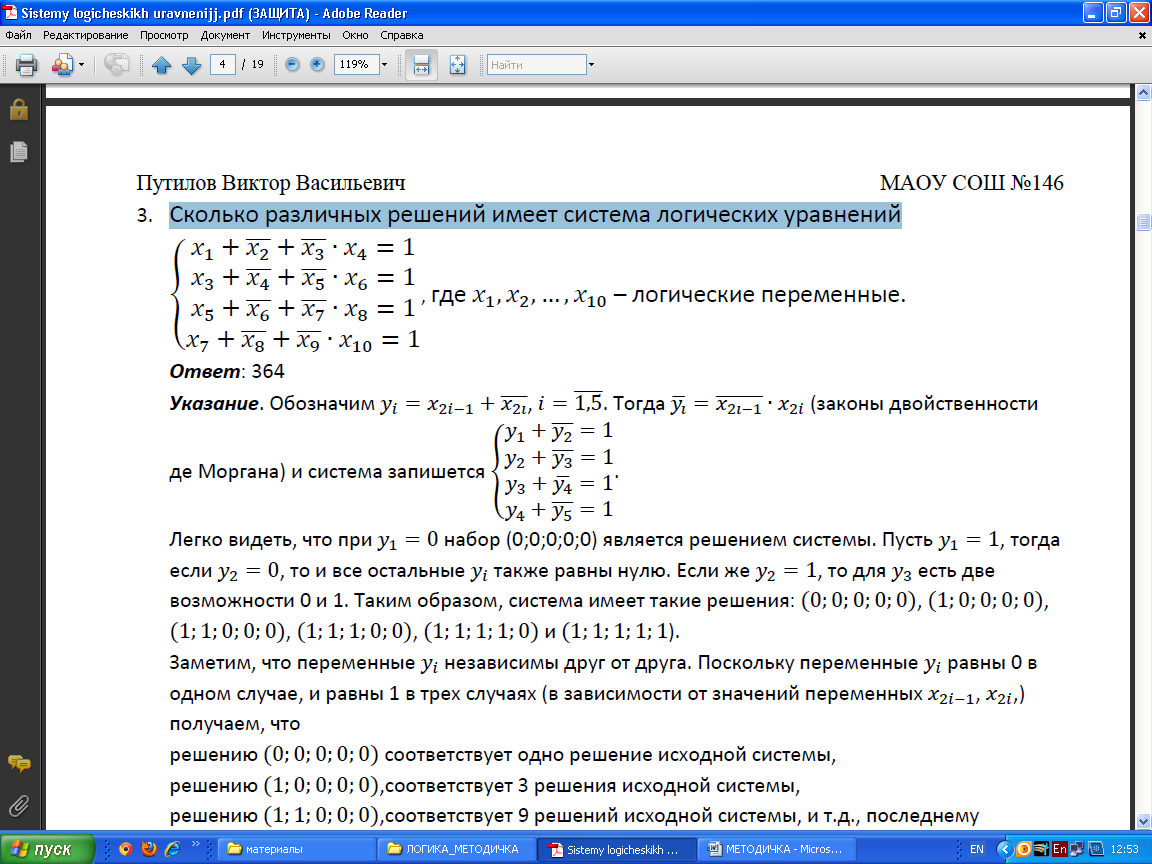
где x ₁, x ₂,… x ₁₀ – логические переменные.

Обозначим . Тогда  (законы двойственности де Моргана) и система запишется

Легко видеть, что при y ₁ = 0 набор (0;0;0;0;0) является решением системы. Пусть y ₁ = 1 тогда если Y ₂ = 0,то и все остальные Y_i также равны нулю. Если же y ₂ = 1, то для y₃ есть две возможности 0 и 1. Таким образом система имеет такие решения (0;0;0;0;0), (1;0;0;0;0), (1;1;0;0;0), (1;1;1;0;0), (1;1;1;1;0), (1;1;1;1;1).

Заметим, что переменные y_i независимы друг от друга. Поскольку переменные y_i равны 0 в одном случае, и равны 1 в трех случаях (в зависимости от значений переменны х _{2 i -1}, x _{2 i},) получаем, что

Решению (0;0;0;0;0) соответствует одно решение исходной системы

Решению (1;0;0;0;0) соответствует 3 решения исходной системы

Решению (1;1;0;0;0) соответствует 9 решений исходной системы, и т.д последнему решению (1;1;1;1;1).соответствует 3³ = 243 различных решения. Таким образом всего исходная система имеет

1 + 3 + 3² +…+ = 364 решения.

 

Пример 5

Сколько решений имеет система логических переменных

 

где x _i, y _i, i = – логические переменные

Здесь дополнительным условием является уравнение, связывающее переменные x ₁ и y ₁. Рассмотрим первое уравнение системы. Очевидно, что оно имеет 6 решений:

 

(0;0;0;0;0), (0;1;1;1;1), (0;0;1;1;1), (0;0;0;1;1), (0;0;0;0;1), (1;1;1;1;1),

 

В первых 5 случаях из последнего уравнения следует, что y₁=1, и тогда, из второго уравнения, все y _i = 1, для i = 1,5. Т. е. имеем 5 различных решений. Если же x ₁ = 1, то из последнего уравнения y ₁ = 1 или y ₁ = 0. В первом случае все y _i=1, для. i = 1,5 – еще одно решение. В первом случае когда решение первого уравнения суть (1;1;1;1;1), получаем также 6 наборов для y _i, как бы выписаны для x _i. Таким образом получили 6 решений. И всего 11.

Пример 6

 

Сколько различных решений имеет система уравнений

 

,

 

где х ₁, х ₂, …, х ₁₀ – логические переменные.

Дополнительное условие в этой задаче – уравнение х ₁ ≡ х ₁₀ = 0

Заметим, что .

Тогда систему можно записать

 

 

Из последнего уравнения имеем, что существуют два набора переменных, при { х ₁; х ₂} при которых последнее уравнение справедливо. Тогда из первого уравнения получаем х ₂ – любое (х ₂ совпадает либо с х ₁, либо с х ₁₀). Таким образом, в этом случае получаем 2 решения (для двух возможных значений переменной х ₁₀). Если же х ₂ ≡ х ₁₀, то из второго уравнения получаем х ₃ – любое. Если х ₃ ≡ х ₁₀, то из третьего уравнения х ₄ ≡ х ₃ ≡ х ₁₀ и, следовательно х ₉ ≡ х ₈ ××× ≡ х ₃ ≡ х ₁₀,. Таким образом, в этом случае снова получаем 2 решения. Если же х ₃ ≡ х ₁, то из третьего уравнения получаем х ₄ – любое. Повторяя указанные рассуждения для всех оставшихся уравнений системы, получаем, что система имеет такие решения:

(х ₁; х ₂ = х ₃ = ××× ≡ х ₁₀), (х ₁ = х ₂; х ₃ = х ₄ = ××× ≡ х ₁₀),

(х ₁ = ××× = х ₃; х ₄ = х ₅ = ××× ≡ х ₁₀), …, (х ₁ = х ₂ = ××× х ₉; х ₁₀)

для каждой пары значений (х ₁; х ₁₀). Значит, система имеет 18 различных решений.

Этот же результат можно получить при помощи построения дерева. Пусть х ₁ = 1, тогда х ₁₀ = 0. Если на каком-то этапе одна из переменных х _i ≡ х ₁₀, то все оставшиеся переменные также эквивалентны х ₁₀. В приводимой ниже таблице показано, как строится дерево. Легко видеть, что при наличии n (n >=2) переменных получаем n решений, т.е. для 9 переменных – 9 решений. Аналогично строится дерево, начиная с х ₁ = 0, х ₁₀ = 1.

Таким образом, снова получаем 18 решений.

 

 

 

Пример 7

 

Сколько различных решений имеет система логических уравнений

 

Заметим, что . Тогда систему можно записать

 

или, переходя к отрицаниям по законам да Моргана,

 

 

  Уравнения системы имеют вид . Составим таблицу истинности для такого уравнения (при входах a и b). В последнем столбе таблицы приведены возможные значения переменной с для выполнения равенства.

 

a	b	с
0	0	0 ½ 1
0	1	0
1	0	1
1	1	0½1

      

Из таблицы видно, что для удовлетворения равенства в случае равенства двух входов a и b, третий параметр может быть произвольным, в случае, когда входы a и b, противоположны, то параметр с должен принимать такое же значение, как и параметр а. Поэтому если в решении системы значения переменных начинают чередоваться, то так продолжается до окончания переменных. Значит, начиная с х (или с х ₁ = 1) мы получаем такие решения:

 

х 1 = 0	х 1 = 1
(0;0;0;0;0;0;0;0;0;0) (0;1;0;1;0;1;0;1;0;1) (0;0;1;0;1;0;1;0;1;0) (0;0;0;1;0;1;0;1;0;1) (0;0;0;0;1;0;1;0;1;0) … (0;0;0;0;0;0;0;0;0;1)	(1;1;1;1;1;1;1;1;1;1) (1;0;1;0;1;0;1;0;1;0) (1;1;0;1;0;1;0;1;0;1) (1;1;1;0;1;0;1;0;1;0) (1;1;1;1;0;1;0;1;0;1) … (1;1;1;1;1;1;1;1;1;0)
10 решений	10 решений

 

Таким образом, система имеет всего 20 решений.

Пример 8

Найти количество решений системы уравнений:

 

гдех ₁ …х ₁₀ –неизвестные логические величины.

Здесь, так же как и в предыдущей задаче, удобнее всего последовательно решать уравнения и записывать полученные решения в таблицу (дерево рисовать не будем для сокращения записи). Сначала упростим исходные уравнения, заметив, что

 

 

 

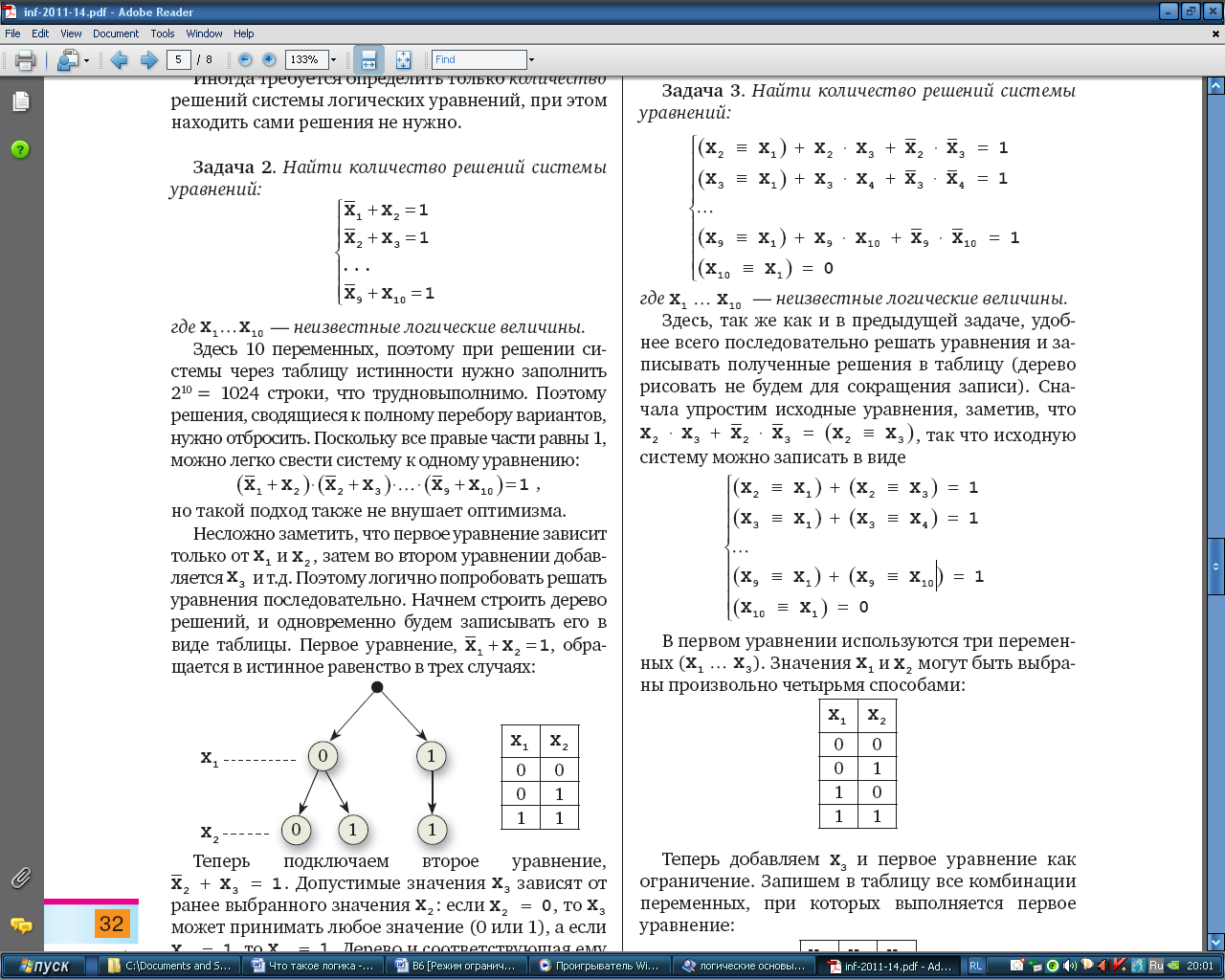
Так что исходную систему можно записать в виде

 

В первом уравнении используются три переменных (x₁ … x₃). Значения x₁ и x₂ могут быть выбраны произвольно четырьмя способами:

Добавляем x₃ и первое уравнение как ограничение. Запишем в таблицу все комбинации переменных, при которых выполняется первое уравнение:

Если x₂ = x₁, то значение x₃ может быть любое (эти строки выделены), а при x₂ ≠ x₁ получаем только один вариант: x₃ = x₂. Таким образом, при подключении первого уравнения число решений увеличивается на количество строк в таблице, для которых значения x₁ и x₂ (последней рассмотренной переменной) равны. В данном случае таких строк две, получаем 6 решений. В новой таблице снова осталось всего две строки (верхняя и нижняя), где x₃ = x₁. Как следует из второго уравнения, именно эти (и только эти) строки на следующем шаге “раздваиваются”, дают по два решения. Таким образом, при подключении к системе очередного уравнения число решений увеличивается на 2. Для двух уравнений получим 8 решений, для трех – 10, а для восьми – 20 решений.

Остается учесть последнее (особое) уравнение, (x₁₀ ≡ x₁) = 0. Это означает, что x₁₀ ≠ x₁. Из анализа таблицы видно, что есть всего две строки (верхняя и нижняя), где первая и последняя переменные равны. Поэтому из полученных 20 решений нужно отбросить эти два, не удовлетворяющие последнему уравнению. В итоге исходная система имеет 18 решений.

 

Пример 9

Найти количество решений системы уравнений:

 

 

где x₁…x₁₀ – неизвестные логические величины.

Сначала упростим эти уравнения, используя свойства операций “исключающее ИЛИ” и “эквивалентность”. В первом уравнении

 

Применяя подобные преобразования во всех уравнениях, получаем

 

Далее замечаем, что можно ввести новые переменные

 

и система уравнений принимает вид

 

 

Важно, что переменные y₁... y₅ независимы, то есть каждая из исходных переменных x₁ … x₁₀ входит только в одну из новых переменных. Полученная система совпадает по форме с системой, которая рассматривалась в задаче 2. Используя результаты решения задачи 2, сразу находим, что наша система из четырех уравнений имеет 6 решений относительно переменных y₁ … y₅. Остается вернуться обратно к исходным переменным x₁ … x₁₀. Предположим, что значение y₁ =(x₁ ≡ x₂) фиксировано (0 или 1). Тогда, согласно таблице истинности операции “эквивалентность”, существует ровно две пары значений (x₁, x₂), при которых y₁ имеет заданное значение (как для y₁ = 0, так и для y₁ = 1). Таким образом, каждая комбинация значений y₁ … y₅ дает по две возможных  пары  (x₁, x₂), (x₃, x₄), (x₅, x₆), (x₇, x₈) и (x₉, x₁₀),  то  есть  всего 2₅ = 32 комбинации исходных переменных. Таким образом, общее количество решений равно 6 · 32 = 192.

 

Пример 10

Найти логическую функцию Х(A, B), которая при любых значениях логических переменных A и B удовлетворяет системе уравнений:

 

 

Классические методы решений систем уравнений, известные из математики, здесь не работают, потому что для логических величин не определено вычитание и деление. Такие системы проще всего решать с помощью таблиц истинности. Для каждой возможной комбинации значений переменных A и B получаем систему уравнений с одним неизвестным X:

Заметим, что в последней строчке значение X может быть любым. Поэтому исходной системе удовлетворяют две логические функции, которые задаются таблицами истинности

 

В первом случае получаем .

а во втором – 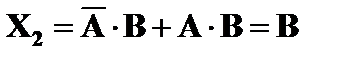. Исходная система уравнений имеет два решения. Логические уравнения такого типа не всегда имеют решение в двузначной логике. Например, уравнение  не имеет решений, потому что при A = B = 0 получаем X = X, что невыполнимо.

 

 

Варианты заданий

 

Решите задачу1 различными способами

Решите задачу 2 с помощью диаграмм

Вариант 1

1. Андрею, Саше и Егору предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Андрей показал, что преступники скрылись на синем Мерседесе, Саша сказал, что это был черный Джип, а Егор утверждал, что это был Форд Мустанг и ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо марку машины, либо только ее цвет. Какого цвета и какой марки была машина?

2. В спортивной делегации 83 человека владеют английским языком, 75 – знают французский, 10 – не знают ни английского, ни французско­го языков. Сколько человек владеют обоими иностранными языками, если численность делегации 100 человек?

3. Сколько различных решений имеет система уравнений

 

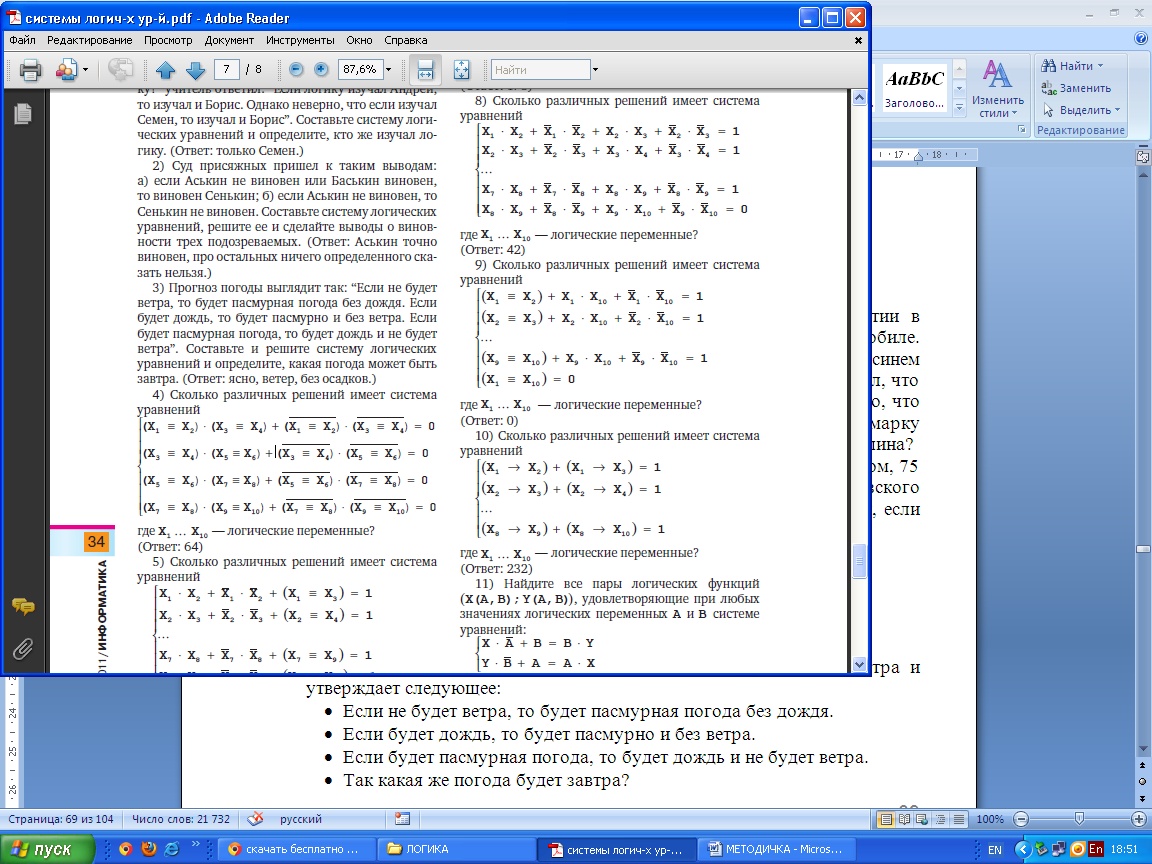
Вариант 2

1. По телевизору с иноптик объявляет прогноз погоды на завтра и утверждает следующее:

· Если не будет ветра, то будет пасмурная погода без дождя.

· Если будет дождь, то будет пасмурно и без ветра.

· Если будет пасмурная погода, то будет дождь и не будет ветра.

· Так какая же погода будет завтра?

2. В одной группе 11 студентов увлекаются лыжным спортом и столько же велоспортом, а плаванием занимаются 14 человек. Лыжами и плаванием увлекаются четверо, а плаванием и велоспортом – двое. Занимающихся одновременно тремя видами спорта нет. Из 45 учащихся класса 15 человек спортом не увлекаются вовсе. Сколько человек занимается лыжным и велосипедным спортом одновременно?

3. На вопрос “Кто из твоих учеников изучал логику?” учитель ответил: “Если логику изучал Андрей, то изучал и Борис. Однако неверно, что если изучал Семен, то изучал и Борис”. Составьте систему логических уравнений и определите, кто же изучал логику.

Вариант 3

1. На вопрос о погоде на завтра синоптик ответил:

· Если будет мороз, то пойдет снег и будет пасмурно.

· Если не будет мороза и пойдет снег, то будет пасмурно.

· Пойдет снег, если будет пасмурно.

· Не верно, что если не будет мороза, то будет пасмурно.

Какая будет погода завтра?

2. На бригантине живут 60 пиратов. 37 из них вечером пьют чай. 33 – курят трубку, 42 – играют в кости. При этом 21 из них пьют чай и курят трубку. 23 – играют в кости и курят трубку, 22 – играют в кости и пьют чай. Только 20 пиратов занимаются одновременно тремя делами: пьют чай, играют в кости и курят трубку. Так ли это. Сколько по – Вашему пиратов было на бригантине?

3. Суд присяжных пришел к таким выводам: если Аськин не виновен или Баськин виновен, то виновен Сенькин; если Аськин не виновен, то Сенькин не виновен. Составьте систему логических уравнений, решите ее и сделайте выводы о виновности трех подозреваемых.

 

Вариант 4

1. При составлении расписания на вторник в группе ИС преподаватели высказали просьбы.

· Преподаватель математики: «Желаю иметь первый или второй урок».

· Преподаватель истории: «Желаю иметь первый или третий урок».

· Преподаватель логики: «Желаю иметь второй или третий урок».

Какое расписание будет составлено, если по каждому предмету может быть только один урок.

2. Одноногий Сильвер со своей шайкой обнаружил клад, спрятанный самим Флинтом. Пираты были крайне нетерпеливы – всем хотелось скорее получить свою долю.52 – достались настоящие пиастры, а 30 пиратов получили фальшивые. 12 – достались и фальшивые и настоящие. Сколько всего пиратов нашло сокровища?

3. Прогноз погоды выглядит так: “Если не будет ветра, то будет пасмурная погода без дождя. Если будет дождь, то будет пасмурно и без ветра. Если будет пасмурная погода, то будет дождь и не будет ветра”. Составьте и решите систему логических уравнений и определите, какая погода может быть завтра.

 

Вариант 5

1. Четыре марсианки, оказавшиеся на Земле в 2… году, на вопрос об их возрасте дали ответы:

МИ – 22 года, МЕ – 21 год.

МО – 19 лет, МИ – 21 год.

МА – 21 год, МО – 18 лет.

Все марсианки разных возрастов, притом только данных: 18,19,21,22. В каждом ответе одна часть верна, другая – нет. Сколько лет каждой марсианке?

2. Среди 150 филателистов марки собирают только мальчики. Марки России собирают 67 человек, марки Африки – 48, марки Америки – 34, только марки Росии – 11, только Африки – 7, только Америки – 2. Лишь один филателист собирает марки России, Америки и Африки.

Сколько девочек среди 150 филателистов?

Сколько различных решений имеет система уравнений

 

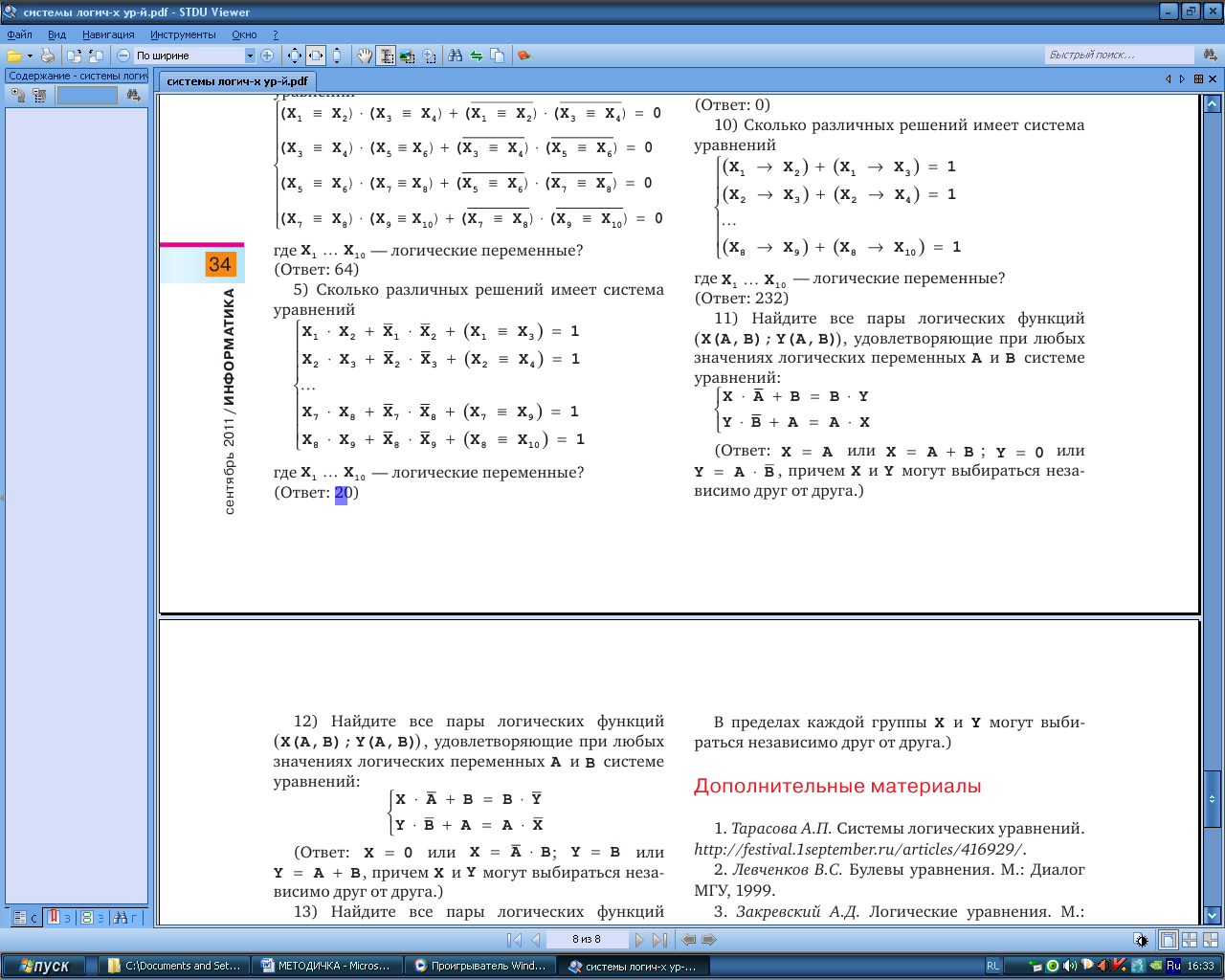
Вариант 6

1. Виновник ночного дорожно-транспортного происшествия скрылся с места аварии. Первый из опрошенных свидетелей сказал работникам ГАИ, что это были “Жигули”, первая цифра номера машины – единица.Второй свидетель сказал, что машина была марки “Москвич”, а номер начинался с семёрки. Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы. При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера. Вопрос. Какой марки была машина и с какой цифры начинался номер?

2. В олимпиаде участвовало 50 человек. Арифметическую задачу решили 30 человек, геометрическую – 10, логическую – 9. Все три задачи решили 2 человека, арифметическую и логическую – 7, арифметическую и геометрическую – 3, логическую и геометрическую – 4. Сколько человек:

· решили арифметическую или геометрическую задачи;

· решили только арифметическую задачу,

· решили арифметическую и логическую задачи, но не решили геоме­трическую задачу;

· решили только логическую задачу;

· решили логическую задачу тогда и только тогда, когда решили геоме­трическую задачу;

· не решили ни одной задачи.

3 Сколько различных решений имеет система уравнений

 

 

 

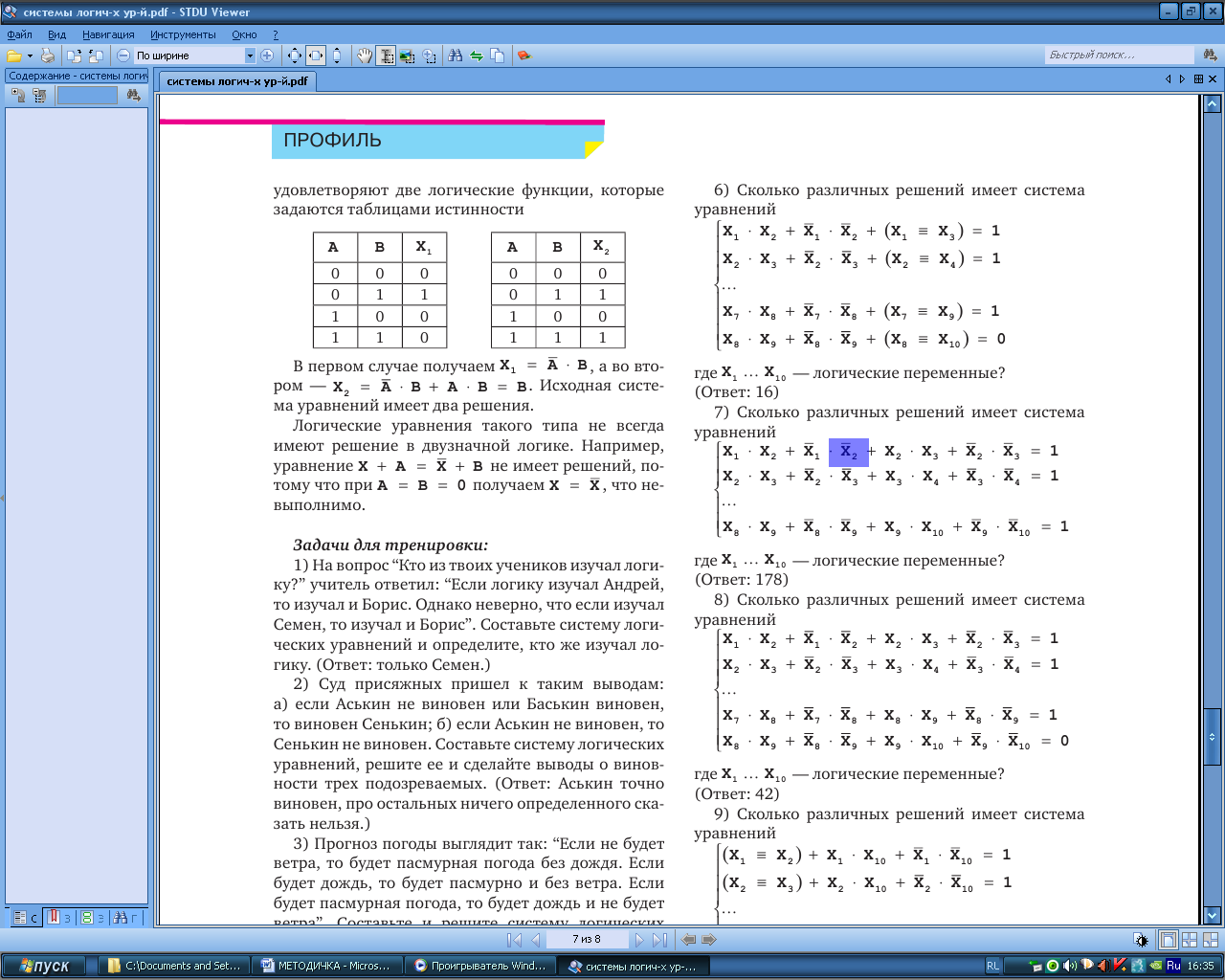
Вариант 7

1. В спортивных соревнованиях принимали участие пять пионерских команд: "Вымпел", "Метеор", "Нептун", "Старт" и "Чайка". Об их итогах соревнования имеется пять высказываний:

· Второе место занял "Вымпел", a "Cтарт" оказался на третьем.

· Хорошо выступала команда "Нептун", она стала победителем, а "Чайка" вышла на второе место.

· Да нет же, " Чайка" заняла только третье место, а "Нептун"- был последним.

· Первое место по праву завоевал "Cтарт", а "Метеор" был четвертым.

· Да, "Метеор" действительно был четвертым, а "Вымпел" был вторым.

· Известно, что команды не делили места между собой и что в каждом высказывании одно утверждение правильное, а другое нет. Как распределились места между командами?

2. В научно-исследовательском институте работает 67 человек. Из них 47 знают английский язык, 35 – немецкий, 23 – английский и немецкий языки. Французский язык знают 20 человек, английский и французский – 12 человек, немецкий и французский – 11 человек, а все три языка – 5 человек. Сколько человек в институте не знают иностранных языков?

3 Сколько различных решений имеет система уравнений

 

где х₁…х₁₀ – логические переменные?

Вариант 8

1. В нарушении правил обмена валюты подозреваются четыре работника банка: A, B, C, D. Известно, что:

· если А нарушил, то и В нарушил правила обмена валюты

· если В нарушил, то С нарушил или А не нарушал

· если D не нарушил, то А нарушил, а С не нарушил

· если D нарушил, то и А нарушил.

Кто из подозреваемых нарушил правила обмена валюты?

2. Анкетирование 100 студентов дало следующие результаты о количестве изучающих различные иностранные языки: английский – 28 человек, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, все три языка – 3. Сколько студентов изучает только английский язык? Только немецкий? Только французский?

3. Сколько различных решений имеет система уравнений

 

 

Вариант 9

1. Аня, Вика и Сергей решили пойти в кино. Максим хорошо знавший этих ребят высказал предположение:

· Аня пойдет в кино только тогда, когда пойдет Вика и Сергей;

· Аня и Сергей пойдут в кино вместе или же оба останутся дома;

· Чтобы Сергей пошел в кино необходимо, чтобы пошла Вика.

Когда ребята пошли в кино оказалось, что из трех утверждений Максима истинны только два. Кто из ребят пошел в кино?

2. В группе 25 студентов. Из них 17 умеют ездить на велосипеде, 13 плавать, а 8 – ходить на лыжах. Ни один из учеников не владеет всеми тремя видами спорта, но как велосипедисты, так и пловцы, и лыжники имеют хорошие или удовлетворительные оценки по математике, что тем более знаменательно, так как 6 студентов в группе имеют неудовлетворительные оценки по этому предмету. Каждый студент -спортсмен за нимается одновременно двумя видами спорта. Сколько студентов имеют отличные оценки по математике? Сколько пловцов умеют ходить на лыжах, сколько велосипедистов умеют плавать и сколько велосипедистов ходят на лыжах?

3. Сколько различных решений имеет система уравнений

Вариант 10

1. На олимпиаде по информатике студенты A, B, C, D заняли четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:

· D – первый или B – второй

· С – первый или А – четвертый

· D – второй или В – третий.

Известно, что в каждом ответе только одно утверждение истинно. Как распределились места?

2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Шестеро знают английский, немецкий – тоже шестеро, французским владеют семеро. Четверо знают английский и немецкий, английский и французский – двое, немецкий и французский – трое. Один человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только немецкий? Только французский?

3. Найдите все пары логических функций (X(A,B);Y(A,B)), удовлетворяющие при любых значениях логических переменных A и B системе уравнений:

 

Вариант 11

1. Кто из учеников A, B, C и D играет, а кто не играет в шахматы, если известно следующее:

· если А или В играет, то С не играет;

· если В не играет, то играют С и D;

· С играет?

2. В туристической группе 30 человек знают французский язык, 30 человек – немецкий и 30 английский. Английский и немецкий – 15, английский и французский – 17, немецкий и французский – 16, а все три языка – 10 человек. Какова численность туристической группы, если 8 че­ловек не владеют данными языками?

3. Найдите все пары логических функций (X(A,B);Y(A,B)), удовлетворяющие при любых значениях логических переменных A и B системе уравнений:

 

Вариант 12

1. В первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.

Один считает, что первой будет Наташа, а Маша будет второй.

Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй. Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?

2. При обследовании сотрудников некоторого научного учреждения выяснилось, что 60 % из них могут читать английскую специальную литературу, 30 % – французскую, 20 % – немецкую, 15 % – и английскую, и французскую, 5 % – английскую и немецкую, 2 % – французскую и немецкую и 1 % может читать на всех трех языках. Спрашивается, каков процент сотрудников, не способных читать ни на одном из трех языков?

3. Найдите все пары логических функций (X(A,B);Y(A,B)), удовлетворяющие при любых значениях логических переменных A и B системе уравнений:

Вариант 13

1. Однажды гномы, решившие отправиться за сокровищами, собрались на совет, чтобы обсудить возможные опасности, которые их ожидают. Было высказано три предложения: либо захватят гоблины, либо нападёт дракон, либо они заблудятся в лесу, либо их ожидают какие – то две, а может быть, и все три из этих опасностей. Если дракон не нападёт, то они утонут в реке. И дракон нападёт, и заблудятся в лесу. Помогавший им волшебник успокоил их и сказал, что второе и третье предположения ложны. Каких же опасностей следует ожидать гномам?

2. Метеорологические наблюдения показали, что из прошедших 80 дней 40 были дождливыми, 55 – ветреными, и только 15 дней погода была хорошей. Сколько дней одновременно были дождливыми и ветреными?

3. Сколько различных решений имеет система уравнений

 

 

где х₁ … х₁₀ – логические переменные?

Вариант 14

1. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники скрылись на синем «Бьюике», Джонс сказал, что это был чёрный «Крайслер», а Смит утверждает, что это был «Форд Мустанг», и ни в коем случае не синий. Стало извест-но, что желая запутать следствие, каждый из них указал правильно либо только марку маши-ны, либо только её цвет. Какого цвета и какой марки был автомобиль?

2. В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?

3. Сколько различных решений имеет система уравнений

Вариант 15

1. Менеджер банка должен установить 4 банкомата. В течение каждого дня работы должны выполняться следующие условия:

· Если работает первый банкомат, то третий банкомат не должен работать, а второй и четвёртый должны.

· Если работает третий банкомат, то первый и четвёртый не должны работать, а второй должен.

· Должен работать по крайней мере один банкомат.

Необходимо определить наибольшее число дней, которое могут работать банкоматы при выполнении этих условий, так, чтобы их назначение ни в один из дней не повторялось, а также указать допустимое расписание на каждый день.

2. Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

3. Решите систему логических уравнений

 

 

Контрольные вопросы

 

1. Описать метод решения логической задачи с помощью рассуждений.

2. Описать метод решения логической задачи средствами алгебры логики.

3. Описать графический способ решения логической задачи.

4. Описать метод решения логической задачи с помощью графа.

5. Описать метод решения задач на компьютере

6. Описать метод решения логических задач с помощью электронных таблиц.

7. Описать метод решения логических задач с помощью диаграмм.

8. Описать метод решения логических задач табличным способом

 

ЛАБОРАТОРНАЯ РАБОТА №3