Таблица истинности – это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.
Таблицы истинности применяются для:
· вычисления истинности сложных высказываний;
· установления эквивалентности высказываний;
· определения тождественно-истинных (тавтологий) и тождественно-ложных высказываний.
Примеры решения задач
Пример 1
Установить истинность высказывания  · С.
· С.
Решение. В состав сложного высказывания входят 3 простых высказывания: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные ситуации. Простые высказывания от сложных отделяются двойной вертикальной чертой.
При составлении таблицы надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться “изнутри наружу”, т. е. от элементарных формул к более и более сложным; столбец, заполняемый последним, содержит значения исходной формулы.
| А
| В
| С
| 
| А+ 
| 
|  · С · С
|
| 0
| 0
| 0
| 1
| 1
| 0
| 0
|
| 0
| 0
| 1
| 1
| 1
| 0
| 0
|
| 0
| 1
| 0
| 0
| 0
| 1
| 0
|
| 1
| 0
| 0
| 1
| 1
| 0
| 0
|
| 1
| 0
| 1
| 1
| 1
| 0
| 0
|
| 0
| 1
| 1
| 0
| 0
| 1
| 1
|
| 1
| 1
| 0
| 0
| 1
| 0
| 0
|
| 1
| 1
| 1
| 0
| 1
| 0
| 0
|
Из таблицы видно, что данное высказывание истинно только в случае, когда А = 0, В = 1, С = 1. Во всех остальных случаях оно ложно.
Пример 2
Установить истинность высказывания.

Решение
| А
| В
| С
| 
| 
| 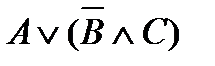
| 
|
| 0
| 0
| 0
| 1
| 0
| 0
| 1
|
| 0
| 0
| 1
| 1
| 1
| 1
| 0
|
| 0
| 1
| 0
| 0
| 0
| 0
| 1
|
| 0
| 1
| 1
| 0
| 0
| 0
| 1
|
| 1
| 0
| 0
| 1
| 0
| 1
| 0
|
| 1
| 0
| 1
| 1
| 1
| 1
| 0
|
| 1
| 1
| 0
| 0
| 0
| 1
| 0
|
| 1
| 1
| 1
| 0
| 0
| 1
| 0
|
Вывод. Высказывание  истинно, когда:
истинно, когда:
А) Aº0; Bº0; Cº0; Б) Aº0; Bº1; Cº0; В) Aº0; Bº1; Cº1.
Пример3
Установить истинность высказываний:
((X1®X2)®X3)Ù(X3«X1)
Решение.
|
|
|
| F1
| F2
| F3
|
|
| X1
| X2
| X3
| X1®X2
| F1®X3
| X3«X1
| F2ÙF3
|
| 0
| 0
| 0
| 1
| 0
| 1
| 0
|
| 0
| 0
| 1
| 1
| 1
| 0
| 0
|
| 0
| 1
| 0
| 1
| 0
| 1
| 0
|
| 0
| 1
| 1
| 1
| 1
| 0
| 0
|
| 1
| 0
| 0
| 0
| 1
| 0
| 0
|
| 1
| 0
| 1
| 0
| 1
| 1
| 1
|
| 1
| 1
| 0
| 1
| 0
| 0
| 0
|
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
Вывод. Высказывание ((X1®X2)®X3)Ù(X3«X1) истинно, когда:
1) X1º1; X2º0; X3º0; 2) X1º1; X2º1; X3º1
Пример 4
Установить истинность высказываний:
((X®Y)Ù(Y®Z))®(X®Z)
Решение.
|
|
|
| F1
| F2
| F3
| F4
|
|
| X
| Y
| Z
| X®Y
| Y®Z
| F1ÙF2
| X®Z
| F3®F4
|
| 0
| 0
| 0
| 1
| 1
| 1
| 1
| 1
|
| 0
| 0
| 1
| 1
| 1
| 1
| 1
| 1
|
| 0
| 1
| 0
| 1
| 0
| 0
| 1
| 1
|
| 0
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
| 1
| 0
| 0
| 0
| 1
| 0
| 0
| 1
|
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 1
|
| 1
| 1
| 0
| 1
| 0
| 0
| 0
| 1
|
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
Вывод. Высказывание ((X®Y)Ù(Y®Z))®(X®Z) истинно всегда.
Пример 5
Составьте таблицу истинности для логической функции
X = (А ↔ B) Ú (A → (B Ú C))
в которой столбец значений аргумента А представляет собой двоичную запись числа 27, столбец значений аргумента В – числа 77, столбец значений аргумента С – числа 120. Число в столбце записывается сверху вниз от старшего разряда к младшему. Переведите полученную двоичную запись значений функции X в десятичную систему счисления.
Решение
1) Запишем уравнение, используя более простые обозначения операций:
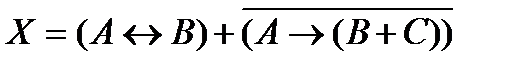
2) Это выражение с тремя переменными, поэтому в таблице истинности будет 23= 8 строчек; следовательно, двоичная запись чисел, по которым строятся столбцы таблицы А, В и С, должна состоять из 8 цифр
| А
| В
| С
| X
|
| 0
| 0
| 0
|
|
| 0
| 1
| 1
|
|
| 0
| 0
| 1
|
|
| 1
| 0
| 1
|
|
| 1
| 1
| 1
|
|
| 0
| 1
| 0
|
|
| 1
| 0
| 0
|
|
| 1
| 1
| 0
|
|
3) Переведем числа 27, 77 и 120 в двоичную систему, сразу дополняя запись до 8 знаков нулями в начале чисел
27 = 000110112 77 = 010011012 120 = = 011110002
4) Составим таблицу истинности. Добавить в таблицу дополнительные столбцы для расчета промежуточных результатов (см. таблицу ниже)
5) Заполняем столбцы таблицы:
| А
| В
| С
| 
| 
| 
| 
| X
|
| 0
| 0
| 0
| 1
| 0
| 1
| 0
| 1
|
| 0
| 1
| 1
| 0
| 1
| 1
| 0
| 0
|
| 0
| 0
| 1
| 1
| 1
| 1
| 0
| 1
|
| 1
| 0
| 1
| 0
| 1
| 1
| 0
| 0
|
| 1
| 1
| 1
| 1
| 1
| 1
| 0
| 1
|
| 0
| 1
| 0
| 0
| 1
| 1
| 0
| 0
|
| 1
| 0
| 0
| 0
| 0
| 0
| 1
| 1
|
| 1
| 1
| 0
| 1
| 1
| 1
| 0
| 1
|
значение  равно 1 только в тех строчках, где А = В
равно 1 только в тех строчках, где А = В
значение  равно 1 только в тех строчках, где В = 1 или С = 1
равно 1 только в тех строчках, где В = 1 или С = 1
значение  равно 0 только в тех строчках, где А = 1 и В + С = 0
равно 0 только в тех строчках, где А = 1 и В + С = 0
значение  – этоинверсия предыдущего столбца (0 заменяется на 1, а 1 – на 0)
– этоинверсия предыдущего столбца (0 заменяется на 1, а 1 – на 0)
результат Х (последний столбец) – это логическая сумма двух столбцов, выделенных фиолетовым фоном
6) чтобы получить ответ, выписываем биты из столбца Х сверху вниз: Х = 101010112
7) переводим это число в десятичную систему: 101010112 = 27 + 25 + 23 + 21 + 20 = 171
8) таким образом, правильный ответ – 171.





 · С.
· С.



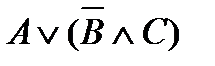
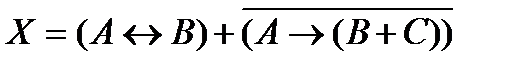




 равно 1 только в тех строчках, где А = В
равно 1 только в тех строчках, где А = В равно 1 только в тех строчках, где В = 1 или С = 1
равно 1 только в тех строчках, где В = 1 или С = 1 равно 0 только в тех строчках, где А = 1 и В + С = 0
равно 0 только в тех строчках, где А = 1 и В + С = 0 – этоинверсия предыдущего столбца (0 заменяется на 1, а 1 – на 0)
– этоинверсия предыдущего столбца (0 заменяется на 1, а 1 – на 0)


