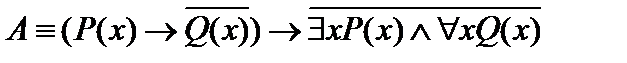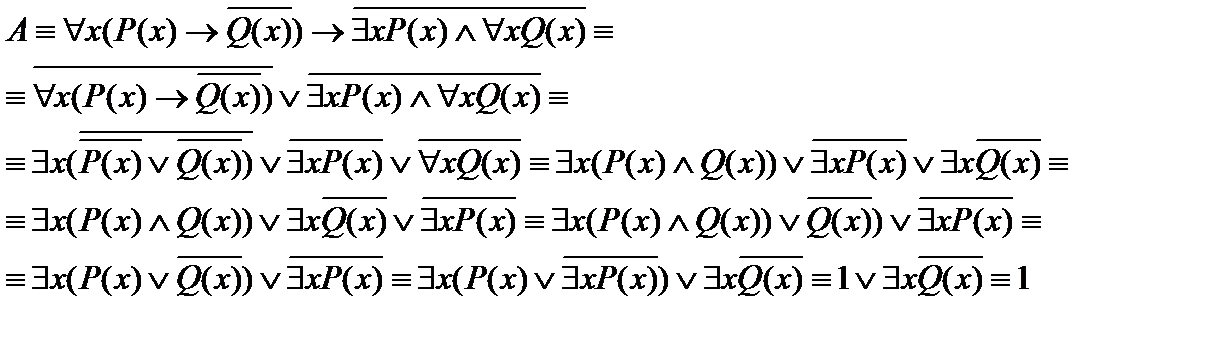Определение 1
Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.
Определение 2
Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.
Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х). Тогда имеют место равносильности:
1. 
2. 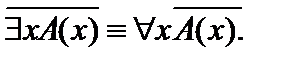
3. 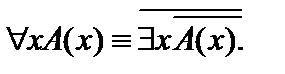
4. 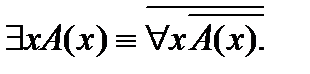
5. 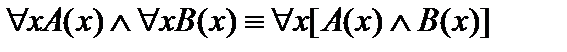
6. 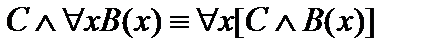 .
.
7. 
8. 
9. 
10. 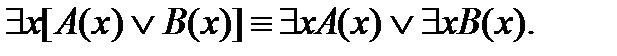
11. 
12. 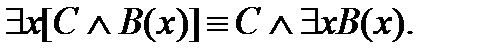
13. 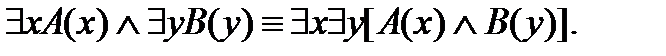
14. 
15. 
Например:
Предикат Мать(x,y) означает, что x является матерью для y, тогда  Мать(x, y) означает, что у каждого человека есть мать, – истинное утверждение.
Мать(x, y) означает, что у каждого человека есть мать, – истинное утверждение.
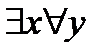 Мать(x, y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно.
Мать(x, y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно.
Таким образом, перестановка кванторов всеобщности и существования может изменить смысл и значение выражения.
Законы логических операций
1. 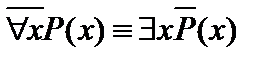 .
.
2. 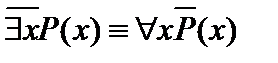 .
.
3.  .
.
4. 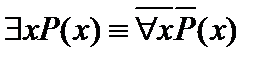 .
.
5.  .
.
6. 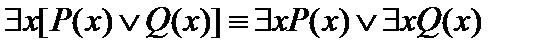 .
.
7. 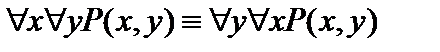 .
.
8. 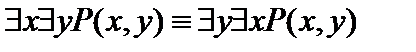 .
.
9. 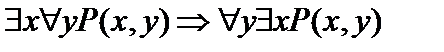 .
.
10.  .
.
11. 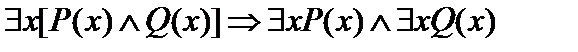 .
.
12. 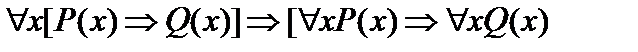 .
. 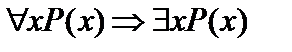 .
.
13.  .
.
14.  .
.
15. 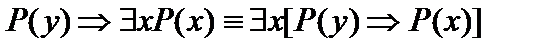
16.  .
.
17.  .
.
18. 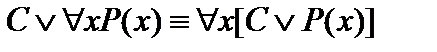 .
.
19.  .
.
20.  .
.
21. 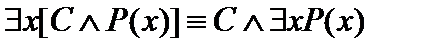 .
.
22. 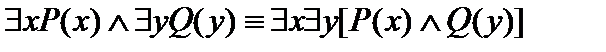 .
.
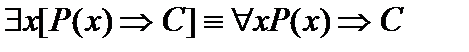 .
.
23. 
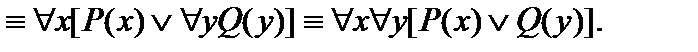
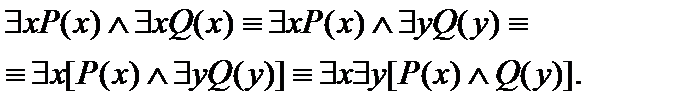
Примеры решения задач
Пример 1. Найти отрицание следующих формул:
А) 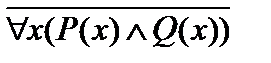 ;
;
Б) 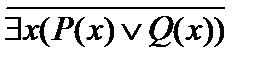 ;
;
В) 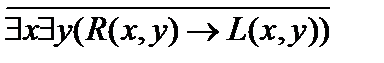
Решение
А)  ;
;
Б) 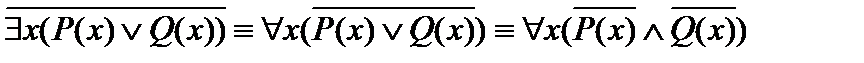 ;
;
В) 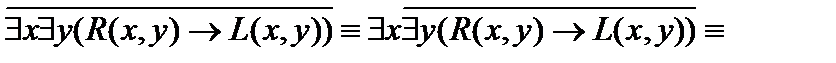
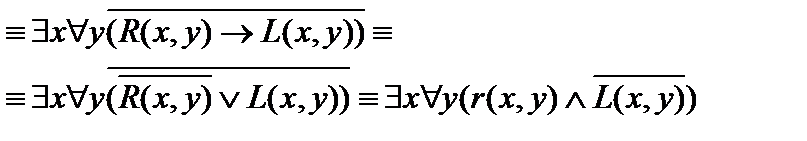
Пример 2. Доказать равносильность:
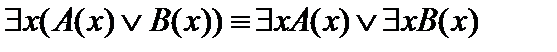
Решение
Для доказательства равносильности достаточно рассмотреть два случая:
1. Пусть предикаты А(х) и В(х) тождественно ложны. Тогда будет ложным и предикат 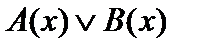 . При этом будут ложными высказывания
. При этом будут ложными высказывания  и
и  .
.
2. Пусть теперь хотя бы один из предикатов (например, А(х)) не тождественно ложный. Тогда будет не тождественно ложным и предикат 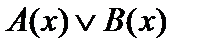 . При этом будут истинными высказывания
. При этом будут истинными высказывания 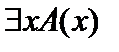 и
и 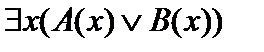 , а значит, будут истинными и исходные формулы.
, а значит, будут истинными и исходные формулы.
Следовательно,  .
.
Пример 3. Доказать равносильность:
 .
.
Решение
Рассмотрим два случая:
1. Пусть высказывание С ложно. Тогда для любого предиката 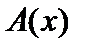 будет ложным высказывание
будет ложным высказывание 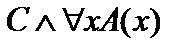 и предикат
и предикат 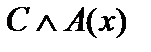 , и, следовательно, высказывание
, и, следовательно, высказывание 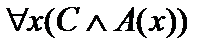 . Значит, в этом случае обе исходные формулы тождественно ложны.
. Значит, в этом случае обе исходные формулы тождественно ложны.
2. Пусть теперь высказывание С истинно. Тогда, очевидно, значения исходных формул будут целиком зависеть от значений предиката А(х). Если А(х) – тождественно истинный предикат, то будет тождественно истинным и предикат 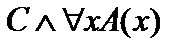 , и, следовательно, будут тождественно истинными высказывания
, и, следовательно, будут тождественно истинными высказывания  ,
, 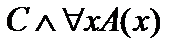 ,
, 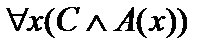 , т. е. тождественно истинны и исходные формулы.
, т. е. тождественно истинны и исходные формулы.
Если А(х) – не тождественно истинный предикат, то будет не тождественно истинным и предикат  , а высказывания
, а высказывания  ,
, 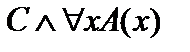 ,
, 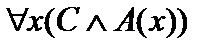 будут ложными, т. е. ложные значения принимают обе исходные формулы, что в итоге доказывает их равносильность.
будут ложными, т. е. ложные значения принимают обе исходные формулы, что в итоге доказывает их равносильность.
Пример 4. Доказать, что формула
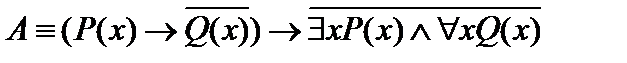
является общезначимой.
Решение
Считая, что формула А определена на любой области М, проведем равносильные преобразования:
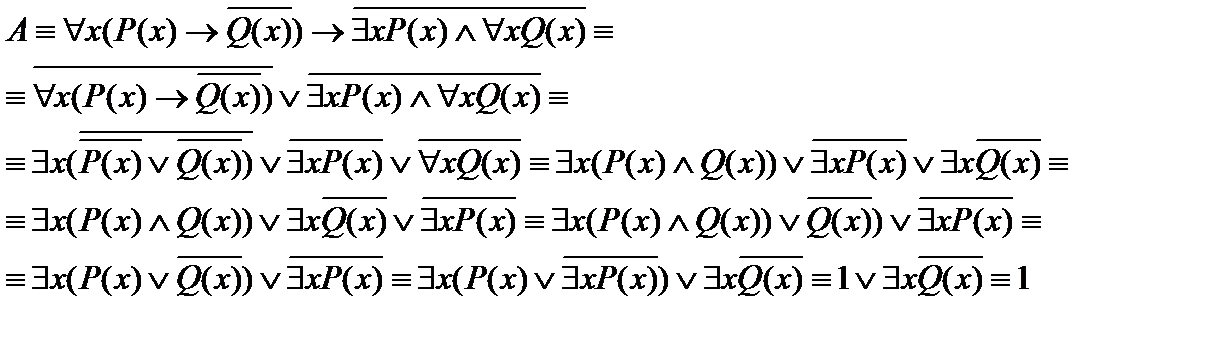
Т. е. формула А тождественно истинна для любых одноместных предикатов Р(х) и Q(х) и в любой области.
Варианты заданий
Задание1
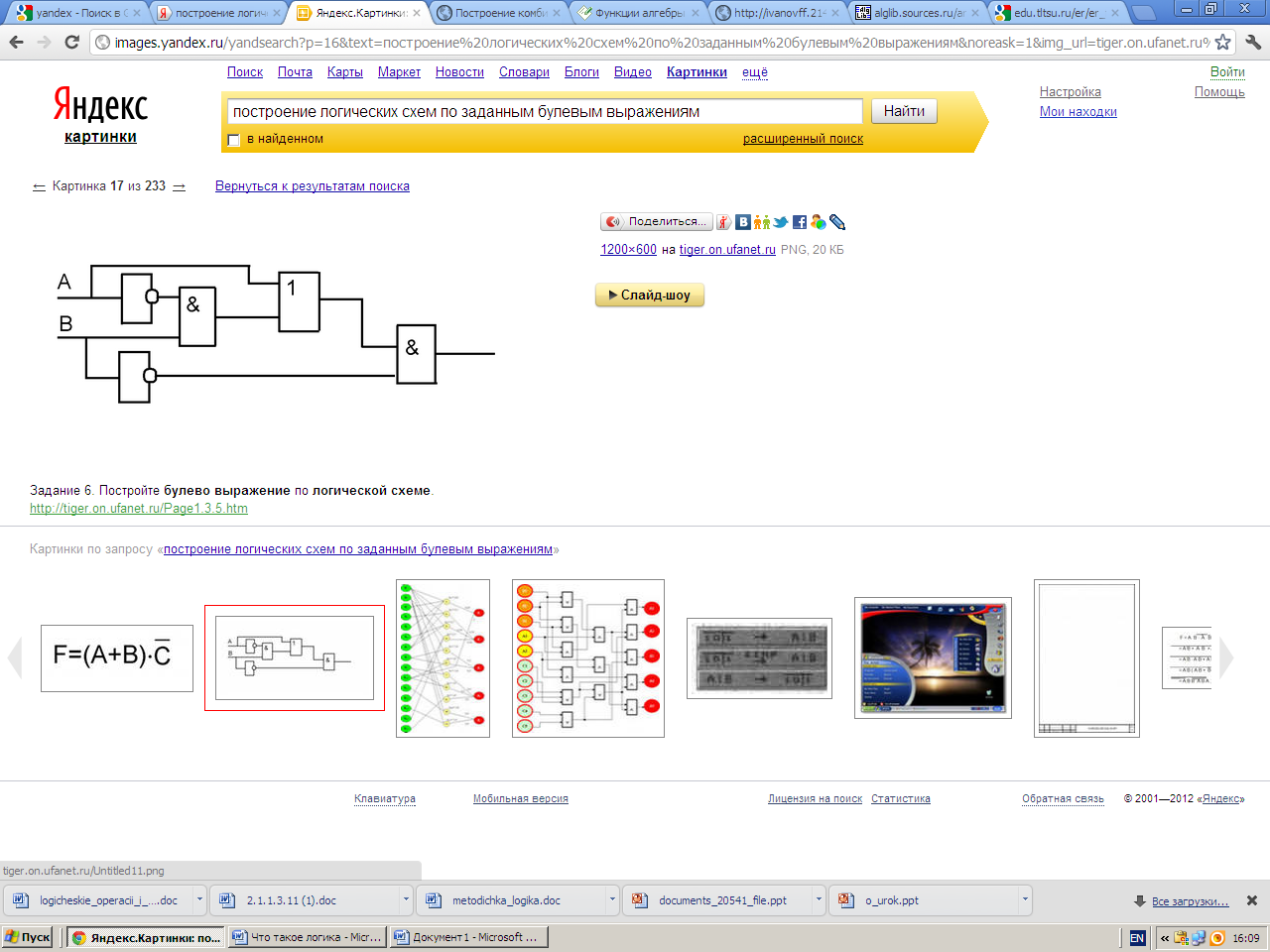
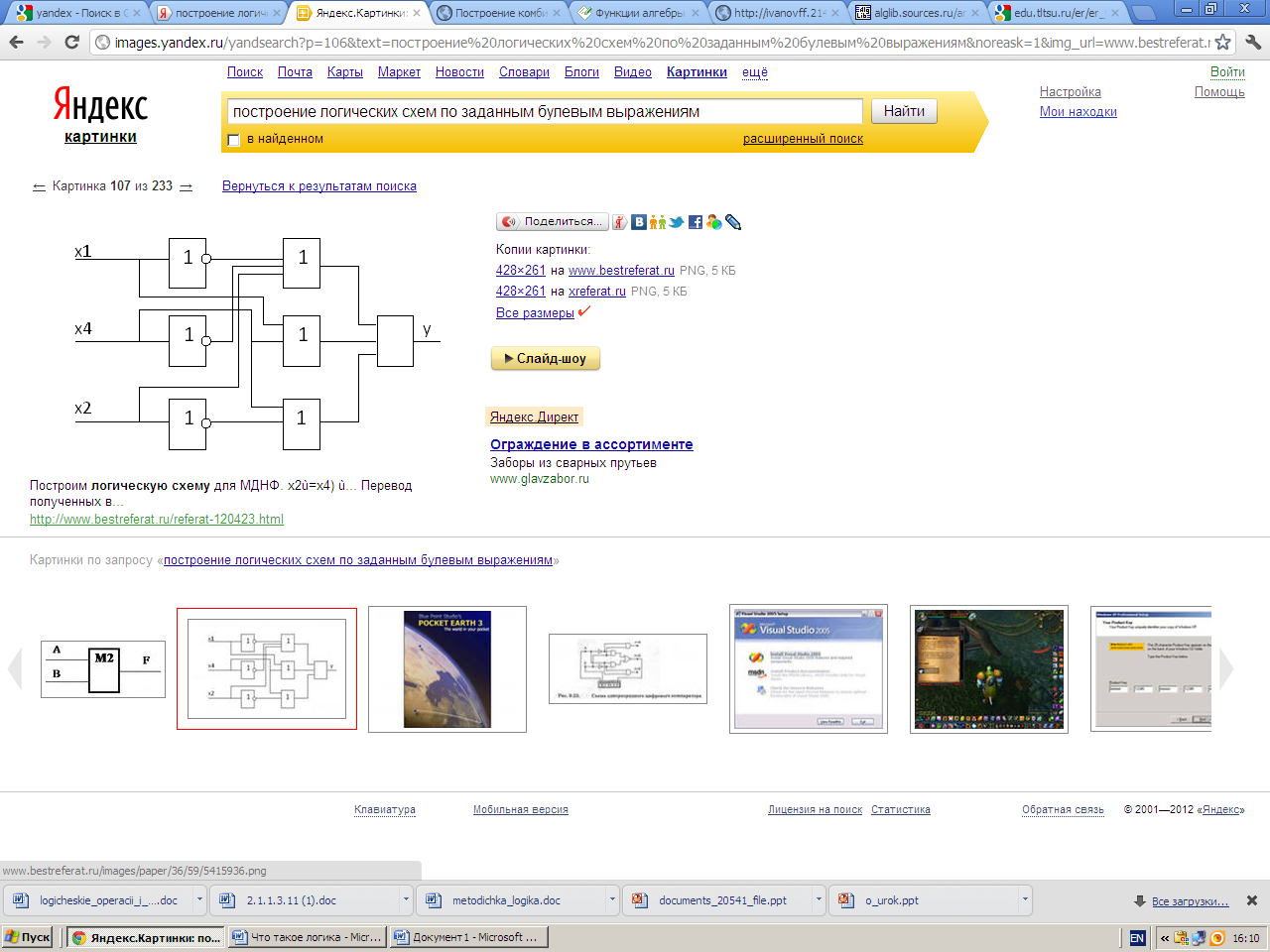
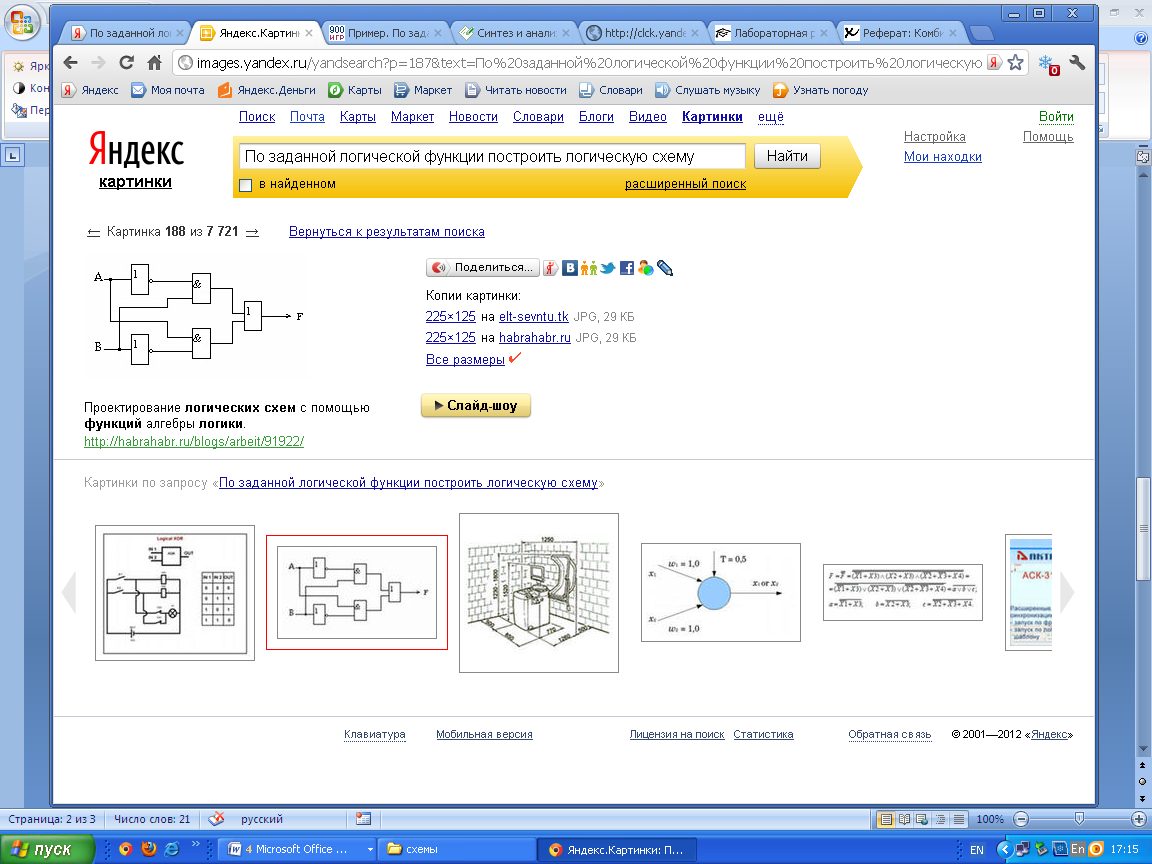
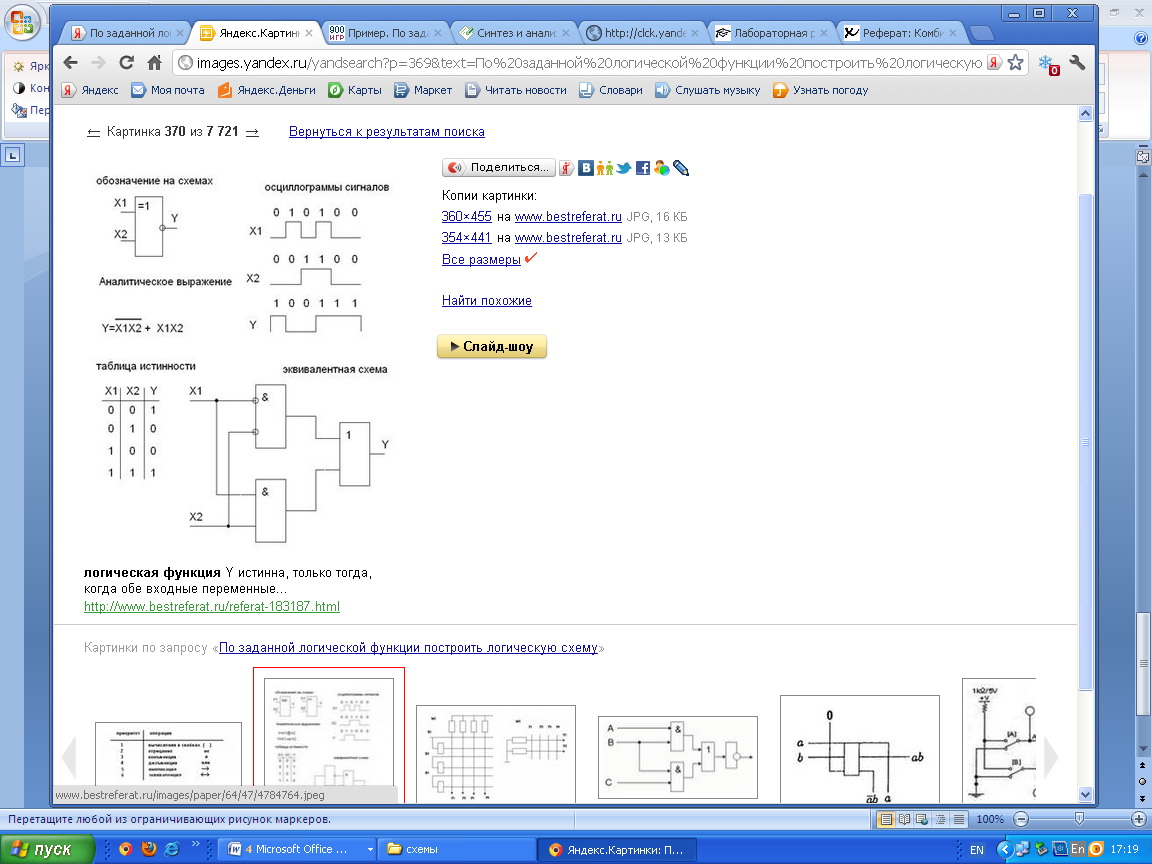
Выписать формулу по заданной функциональной схеме.
Задание2
Построить СДНФ, упростить формулу и построить схему.
Задание 3
Запишите с помощью кванторов заданное утверждение.
| Значения
| Варианты
|
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
|
| X1
| X2
| X3
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
| F
|
| 0
| 0
| 0
| 0
| 0
| 1
| 0
| 1
| 1
| 1
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
|
| 0
| 0
| 1
| 0
| 0
| 1
| 0
| 0
| 0
| 1
| 1
| 0
| 1
| 1
| 0
| 0
| 1
| 0
|
| 0
| 1
| 0
| 0
| 0
| 1
| 1
| 0
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 0
| 0
| 1
|
| 0
| 1
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 0
| 0
| 1
| 0
| 1
| 0
| 1
| 0
|
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 1
| 0
| 0
| 1
| 0
| 1
|
| 1
| 0
| 1
| 1
| 1
| 1
| 0
| 0
| 0
| 1
| 1
| 0
| 0
| 0
| 0
| 0
| 1
| 0
|
| 1
| 1
| 0
| 1
| 0
| 0
| 1
| 0
| 0
| 0
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 0
|
| 1
| 1
| 1
| 0
| 1
| 0
| 0
| 0
| 0
| 0
| 0
| 1
| 0
| 1
| 0
| 1
| 0
| 0
|
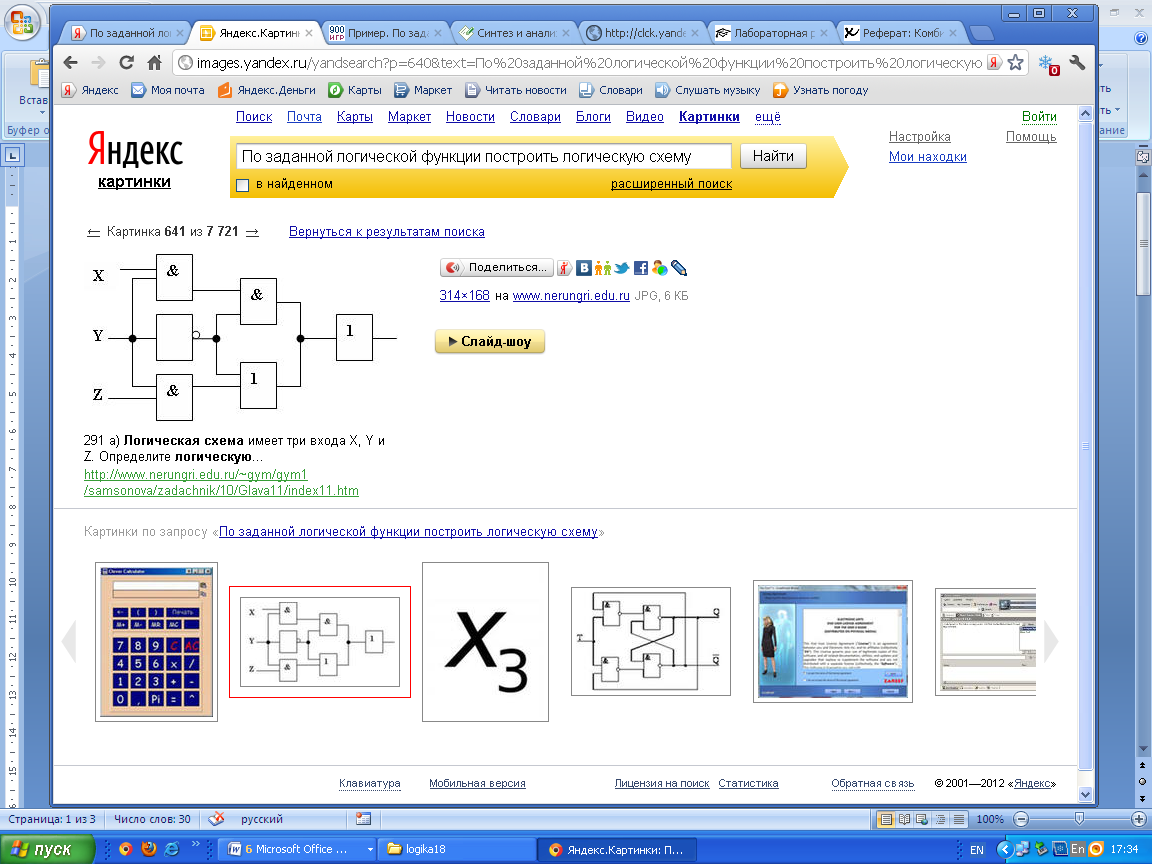
Вариант 1
1. 
2. Запишите с помощью кванторов следующее утверждение:
“Существует x, такой что x > y ”.
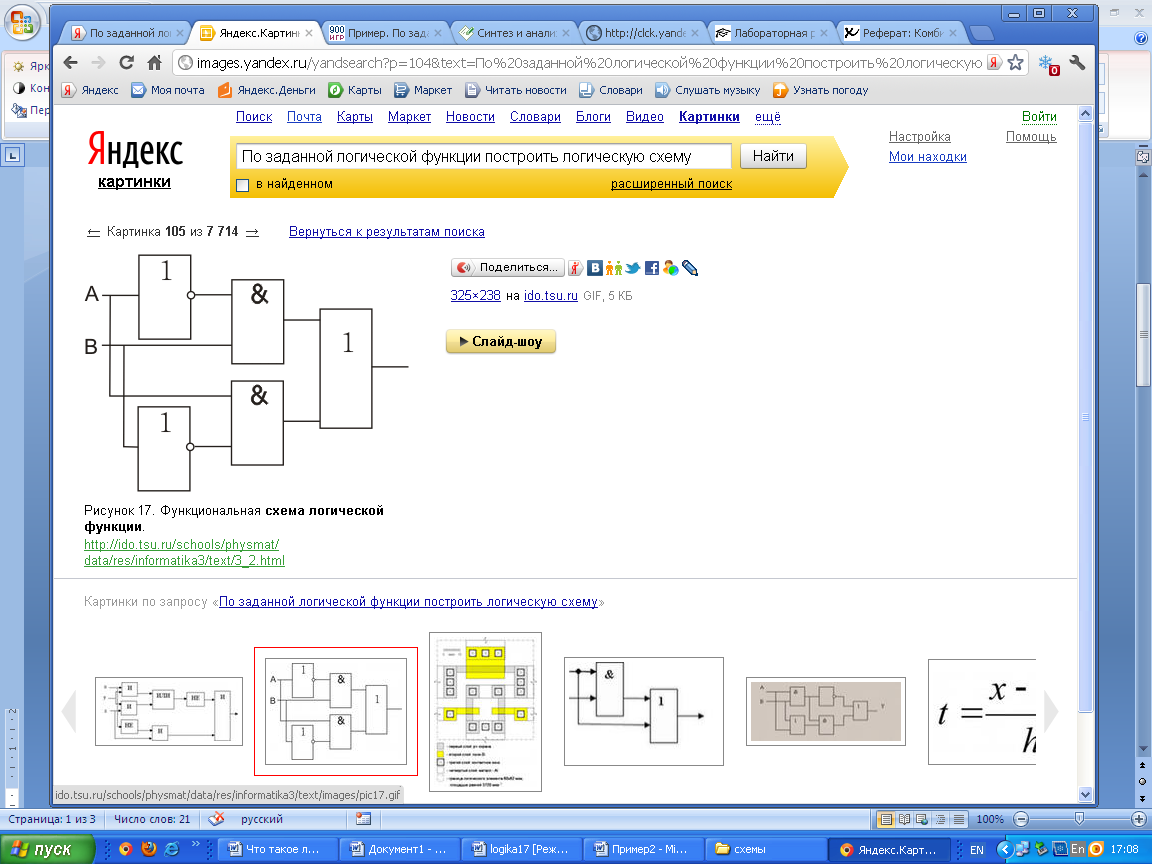
Вариант 2
1. 
2. Запишите с помощью кванторов следующее утверждение:
“Не существует x, такой что x > y”.
Вариант 3
1.
2.Запишите с помощью кванторов следующее утверждение:
“Для любого x имеем x2 > 1”.
Вариант 4
1.
2.Запишите с помощью кванторов следующее утверждение:
“Любая река впадает в Каспийское море”.
Вариант 5
1.
2.Запишите с помощью кванторов следующее утверждение:
“Существует река, которая впадает в Каспийское море”.
Вариант 6
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Для любой реки существует море, в которое она впадает”.
Вариант 7
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Для любого моря существует река, которая в него впадает”.
Вариант 8
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Существует море, в которое впадают все реки”.
Вариант 9
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Существует река, которая впадает во все моря”.
Вариант 10
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Некоторые школьники ходят в театр”.
Вариант 11
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Все кошки серые”.
Вариант 12
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Встречаются злые собаки”.
Вариант 13
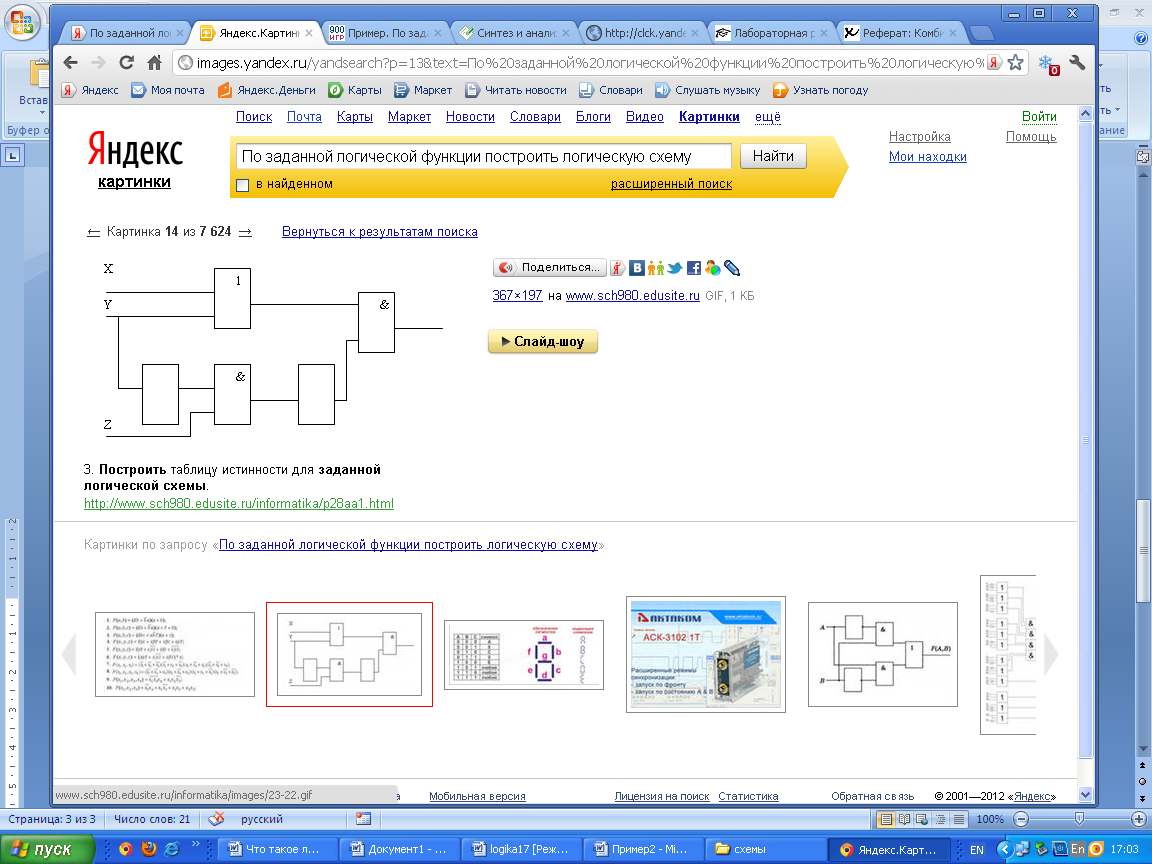
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Все люди разные”.
Вариант 14
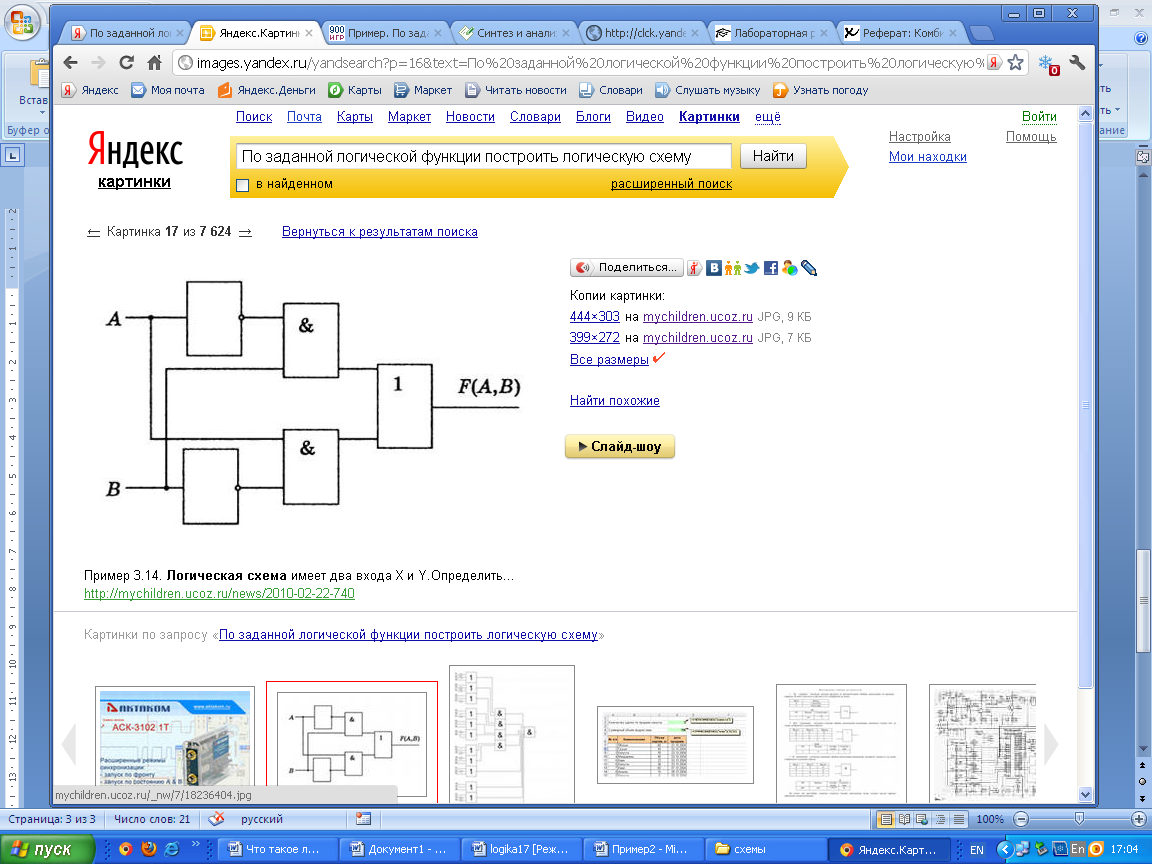
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Никто не обращает на него внимания”.
Вариант 15
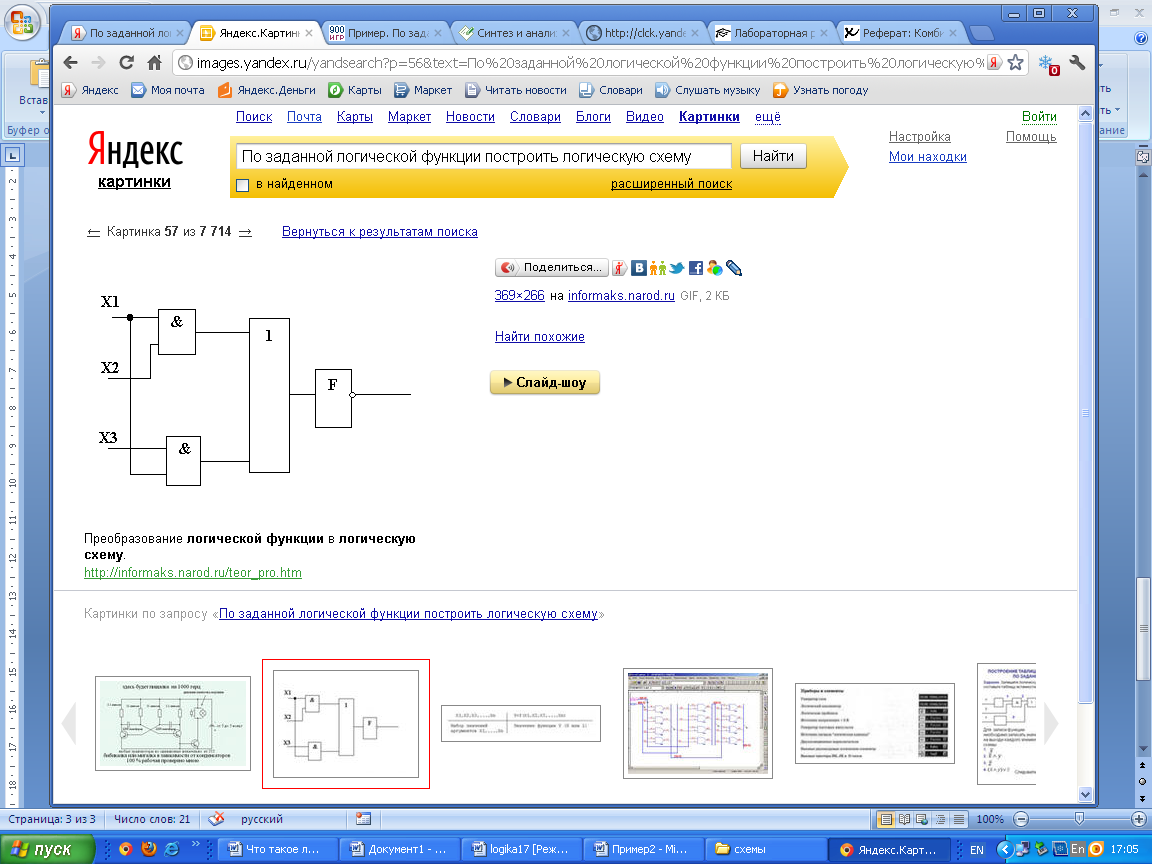
1. 
2.Запишите с помощью кванторов следующее утверждение:
“Ни одна фирма не обанкротилась”.
Контрольные вопросы
1. Условное обозначение на структурных схемах схемы И.
2. Условное обозначение на структурных схемах схемы ИЛИ.
3. Условное обозначение на структурных схемах схемы НЕ.
4. Условное обозначение на структурных схемах схемы И-НЕ.
5. Условное обозначение на структурных схемах схемы ИЛИ-НЕ.
6. Синтез однотактных автоматов. Тригер. Сумматор.
7. Понятие предиката.
8. Понятие Квантора.
СПИСОК ЛИТЕРАТУРЫ
1. Поляков К. Ю., Шестаков А. П., Еремин Е. А. Логические основы компьютера // Информатика №12, 2010.
2. Поляков К. Ю. Системы логических уравнений // Информатика. №9, 2011.
3. Есипов А. С., Паньгина Н. Н., Громада М. И. Информатика. Сборник задач и решений для общеобразовательных учебных заведений. СПб: Наука и Техника, 2001. 368 с.
4. Анкудинов Г. И., Анкудинов И. Г., Петухов О. А. Математическая логика и теория алгоритмов: Учебное пособие. СПб.: СЗТУ, 2002. 104 с.
5. Онегов В. А. Решение логических задач средствами алгоритмических языков // Информатика и образование. №6. 2000.
6. Рыбин С. В. Высказывания и предикаты // Компьютерные инструменты в образовании. №6, 2005.
7. Поляков К. Ю., Шестаков А. П., Еремин Е. А. Информатика. СПб.: Питер, 2011, 274 с.
8. Остряковский В. А, Поляков И. В. Информатика. Теория и практика. М.: Высшее образование, 2008, 608 с.






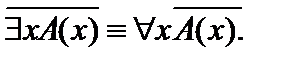
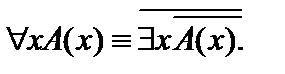
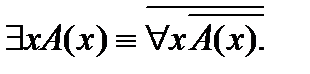
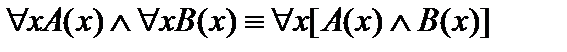
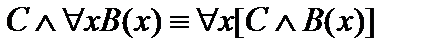 .
.


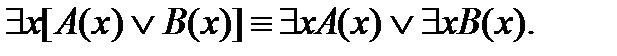

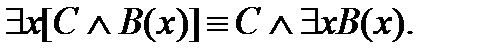
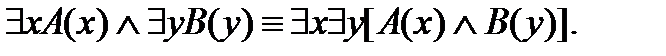


 Мать(x, y) означает, что у каждого человека есть мать, – истинное утверждение.
Мать(x, y) означает, что у каждого человека есть мать, – истинное утверждение.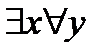 Мать(x, y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно.
Мать(x, y) означает, что существует мать всех людей, что является другим утверждением, истинность которого зависит от множества значений, которые могут принимать y: если это множество братьев и сестер, то оно истинно, а в противном случае оно ложно.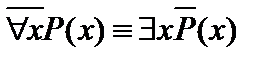 .
.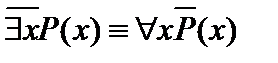 .
. .
.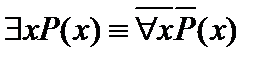 .
. .
.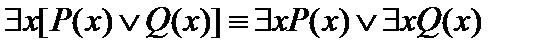 .
.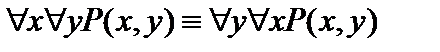 .
.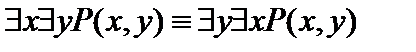 .
.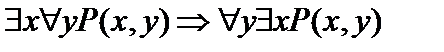 .
. .
.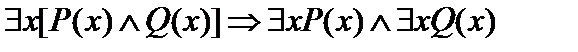 .
.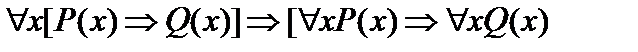 .
. 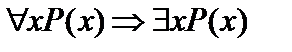 .
. .
. .
.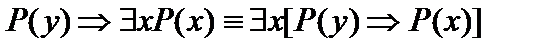
 .
. .
.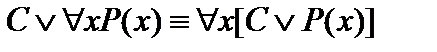 .
. .
. .
.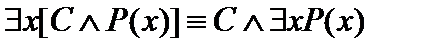 .
.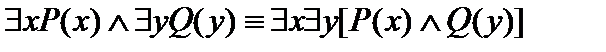 .
.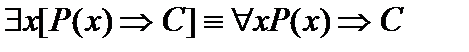 .
.
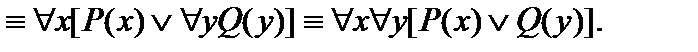
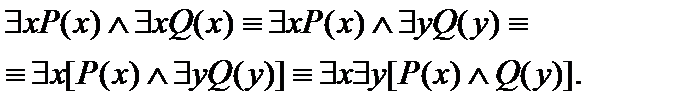
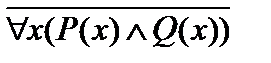 ;
;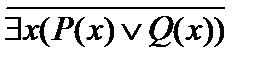 ;
;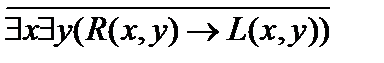
 ;
;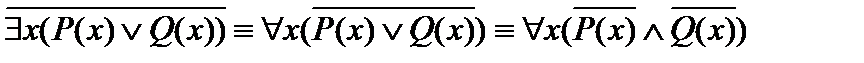 ;
;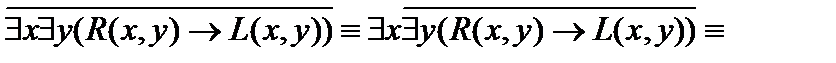
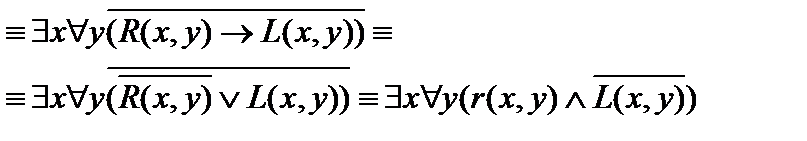
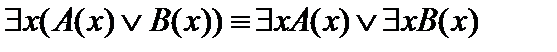
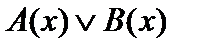 . При этом будут ложными высказывания
. При этом будут ложными высказывания  и
и  .
.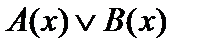 . При этом будут истинными высказывания
. При этом будут истинными высказывания 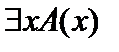 и
и 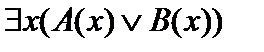 , а значит, будут истинными и исходные формулы.
, а значит, будут истинными и исходные формулы. .
. .
.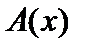 будет ложным высказывание
будет ложным высказывание 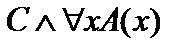 и предикат
и предикат 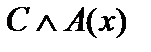 , и, следовательно, высказывание
, и, следовательно, высказывание 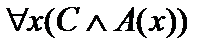 . Значит, в этом случае обе исходные формулы тождественно ложны.
. Значит, в этом случае обе исходные формулы тождественно ложны.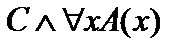 , и, следовательно, будут тождественно истинными высказывания
, и, следовательно, будут тождественно истинными высказывания  ,
, 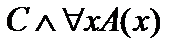 ,
, 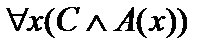 , т. е. тождественно истинны и исходные формулы.
, т. е. тождественно истинны и исходные формулы. , а высказывания
, а высказывания  ,
, 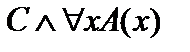 ,
, 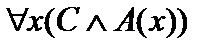 будут ложными, т. е. ложные значения принимают обе исходные формулы, что в итоге доказывает их равносильность.
будут ложными, т. е. ложные значения принимают обе исходные формулы, что в итоге доказывает их равносильность.