Решение логических задач с помощью диаграмм

 

Выражения, зависящие от небольшого количества переменных (обычно не более четырех), удобно изображать в виде диаграмм, которые называют диаграммами Венна, или кругами Эйлера. На такой диаграмме каждой переменной соответствует круг, внутри которого она равна единице, а вне его – нулю. Круги пересекаются, каждый с каждым. Области, в которых рассматриваемое логическое выражение истинно, закрашиваются каким-либо цветом. Ниже приведены диаграммы для простейших операций с одной и двумя переменными. Серым цветом залиты области, где рассматриваемое выражение равно единице.

Такие диаграммы часто используются при работе с множествами: операция “И” соответствует пересечению двух множеств, а “ИЛИ” – объединению.

Для трех переменных диаграмма будет немного сложнее. Для каждой из областей, показанной ниже диаграммы, запишем логические выражения:

 

 

Для того чтобы найти выражение для объединения двух или нескольких областей, надо сложить (используя логическое сложение – операцию “ИЛИ”) выражения для всех составляющих. Например, выражение для объединения областей 3 и 4 имеет вид

С другой стороны, можно заметить, что справедлива формула

Это означает, что логические выражения в некоторых случаях можно упростить.

Диаграммы удобно применять для решения задач, в которых используются множества, например, множества ссылок, полученных от поисковой системы в ответ на какой-то запрос.

Примеры решения задач

Пример 1

В языке запросов поискового сервера для обозначения логической операции "ИЛИ" используется символ "|", а для логической операции "И" – символ "&".

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

 

Запрос	Найдено страниц (в тысячах)
Торты | Пироги	12000
Торты & Пироги	6500
Пироги	7700

 

Какое количество страниц (в тысячах) будет найдено по запросу Торты?

 

Считается, что все запросы выполнялись практически одно 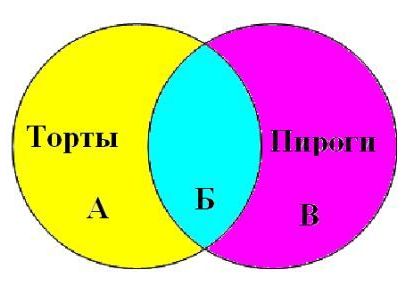временно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Торты │Пироги = А+Б+В = 12000

Торты & Пироги = Б = 6500

Пироги = Б+В = 7700

Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.

Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А+Б = 4300+6500 = 10800

 

 

Пример  2

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции "ИЛИ" используется символ "|", а для логической операции "И" – символ "&".

1	барокко | классицизм | ампир
2	барокко | классицизм & ампир
3	классицизм & ампир
4	барокко | классицизм

Решение

Представим множества классицизм, ампир и классицизм в виде 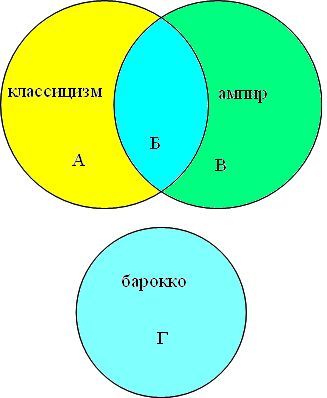кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

 

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

Пример 3

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

 

Для обозначения логической операции "ИЛИ" используется символ "|", а для логической операции "И" – символ "&".

 

1	канарейки | терьеры | содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

 

Для решения задачи представим запросы в виде кругов Эйлера.

K – канарейки,

Щ – щеглы,

С – содержание,

Р – разведение.

Решение

Будем закрашивать сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.

 

канарейки | терьеры | содержание	канарейки &  содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

 

Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1 Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.Только при таких условиях мы можем быть уверены, что правильно решили задачу.

Пример 4

 

Известно количество ссылок, которые находит поисковый сервер по следующим запросам (здесь символ “&” обозначает операцию “И”, а “|” – операцию “ИЛИ”):

собаки  200

кошки  250

лемуры  450

кошки | собаки 450

кошки & лемуры 40

собаки & лемуры 50

Сколько ссылок найдет этот сервер по запросу (кошки|собаки)&лемуры?

Решение

Обозначим буквами С, К и Л высказывания “ключевое слово – собаки”, “ключевое слово – кошки” и “ключевое слово – лемуры”. Построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу (кошки | собаки) & лемуры

На рисунке эта область закрашена цветом.

Выделим три условия

собаки  200

кошки  250

кошки | собаки 450

Это означает, что область “кошки ИЛИ собаки” равна сумме областей “кошки” и “собаки”, то есть эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так:

 

 

Области 1 (собаки & лемуры) и 2 (кошки & лемуры) известны, они составляют соответственно 40 и 50 ссылок, поэтому по запросу (кошки | собаки) & лемуры поисковый сервер выдаст 40 + 50 = 90 ссылок.

 

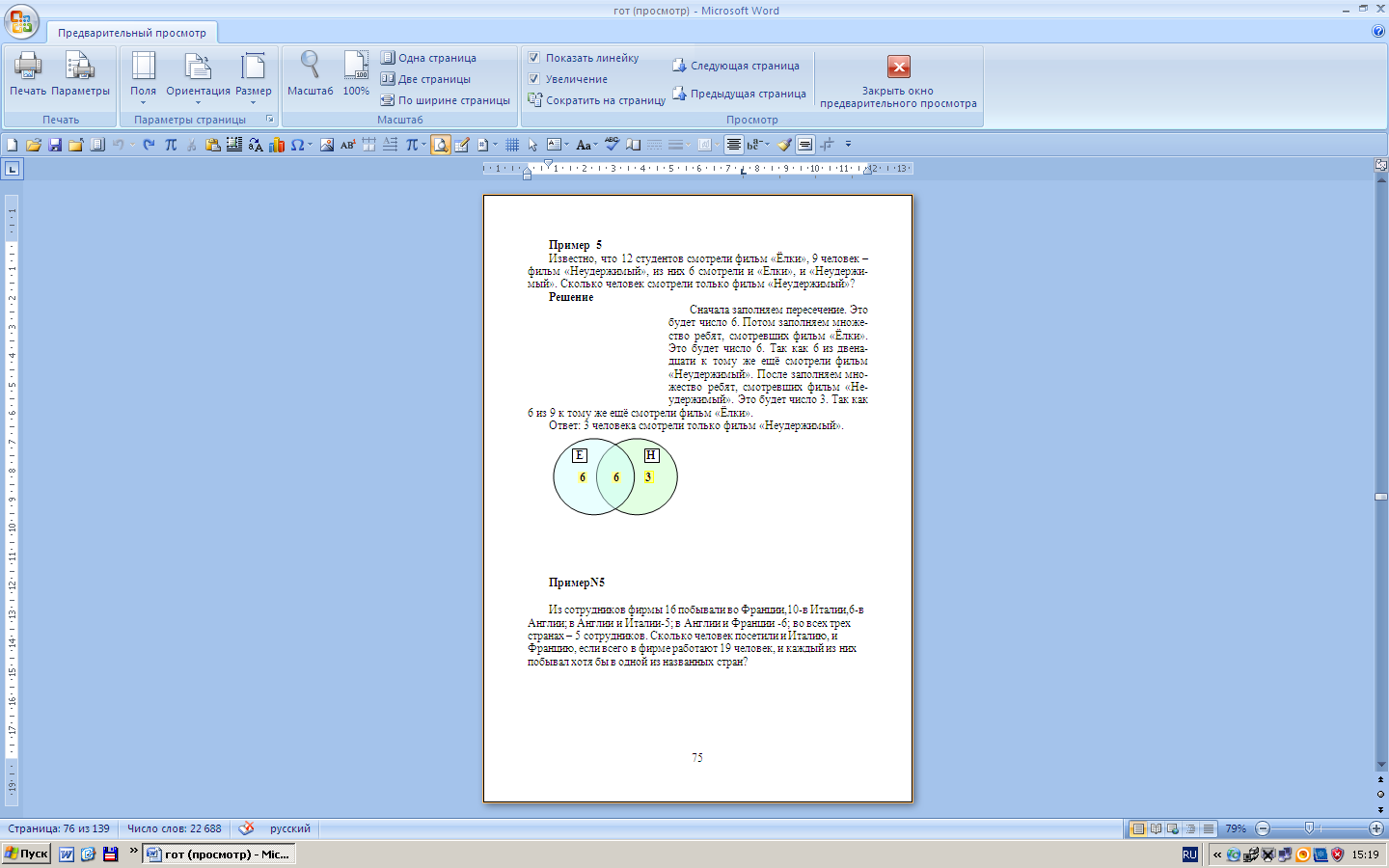
Пример 5

Известно, что 12 студентов смотрели фильм «Ёлки», 9 человек – фильм «Неудержимый», из них 6 смотрели и «Ёлки», и «Неудержимый». Сколько человек смотрели только фильм «Неудержимый»?

Решение

Сначала заполняем пересечение. Это будет число 6. Потом заполняем множество ребят, смотревших фильм «Ёлки». Это будет число 6. Так как 6 из двенадцати к тому же ещё смотрели фильм «Неудержимый». После заполняем множество ребят, смотревших фильм «Неудержимый». Это будет число 3. Так как 6 из 9 к тому же ещё смотрели фильм «Ёлки».

Ответ: 3 человека смотрели только фильм «Неудержимый».

Пример 6

Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Решение

Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пи­шем х – 5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6 – 5 – 1 = 0 пишем 0, во Франции 16 – х + 5 – 6 и Италии 10 – х + 5 – 5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1 + 16 – х + 5 – 6 + 5 + х – 5 + 10 – х + 5 – 5 = 19, отсюда х = 7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.

Пример 7

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?

Решение.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10 – 3 = 7 человек.

5

3

7

30

2

13

Н

А

Ф

20

? 20

100

 

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5 – 3 = 2 туриста.

Немецкий знают 30 человек, но 5 + 3 + 2 = 10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским – 30.

Всего 100 туристов. 20 + 13 + 30 + 5 + 7 + 2 + 3 = 80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.