а) Частоты складываемых колебаний одинаковы.
Предположим, что точка одновременно принимает участие в двух гармонических движениях вдоль одного и того же направления, при этом частоты складываемых колебаний равны между собой, отличаются только амплитуды и начальные фазы колебаний:
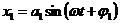 и
и 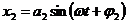
По принципу суперпозиции колебаний полное смещение точки из положения равновесия должно быть равным геометрической сумме смещений, получаемых в каждом из отдельных колебаний. Кроме того, поскольку оба составляющих колебания происходят с одной и той же частотой, то и результирующее колебание будет иметь ту же частоту. Поэтому результат сложения колебаний представим в виде функции:

Используя формулы для тригонометрических преобразований, далее запишем, что:
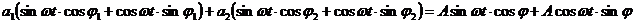
Очевидно, что равенство будет соблюдаться для любого произвольного момента времени, если

Из последних условий можно определить амплитуду и начальную фазу
результирующего колебания
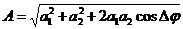 (338)
(338)
Амплитуда результирующего колебания может принимать различные значения в зависимости от значений амплитуд складываемых колебаний и разности их начальных фаз. Например, если фазы складываемых колебаний отличаются на 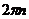 , то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А = а1 + аг если же разность фаз равна (2п + 1)
, то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А = а1 + аг если же разность фаз равна (2п + 1)  , то - разности амплитуд А = а1-аг. При разности фаз, равной нечётному числу
, то - разности амплитуд А = а1-аг. При разности фаз, равной нечётному числу  амплитуда результирующего колебания равна
амплитуда результирующего колебания равна 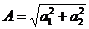 .
.
Этот же результат можно легко получить, пользуясь векторным представлением колебаний, как это указывалось выше.
50. Сложение одинаково направленных колебаний.
б) Частоты складываемых колебаний различны, одинаковы амплитуды и начальные фазы
При складывании колебаний различных частот равенство амплитуд и начальных фаз мы взяли только для упрощения преобразований. Пусть первое из складываемых колебаний имеет вид  , а второе-
, а второе- 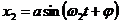 . По принципу суперпозиции колебаний
. По принципу суперпозиции колебаний 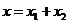 . Используя формулы тригонометрических преобразований, получаем результат в виде:
. Используя формулы тригонометрических преобразований, получаем результат в виде:  (339)
(339)
Как видно, результирующее колебание в этом случае не является гармоническим. Однако, если частоты складываемых колебаний не очень отличаются друг от друга, то результирующее колебание можно представить как почти гармоническое с медленно изменяющейся амплитудой. При этом смещение точки из положения равновесия происходит с частотой, равной полусумме складываемых частот. Такой случай сложного колебания называется биениями, т.е. периодическими изменениями амплитуды результирующего колебания, возникающие при сложении двух одинаково направленных гармонических колебаний с близкими частотами. Частота биений при этом определяется разностью частот складываемых колебаний 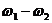 .
.
Практически биения используют для сравнения частот двух колебаний, например, при настройке музыкальных инструментов. Наблюдение биений позволяет с большой точностью определить тот момент, когда частота биений становится равной нулю (так называемые нулевые биения). Это происходит при равенстве частот складываемых колебаний. Похожее явление биений наблюдается и при складывании нормальных колебаний с несколькими степенями свободы. В таких системах в некоторые моменты времени амплитуда колебаний одного из тел системы принимает максимальное значение, в то время как для другого она становится минимальной. Другими словами, в связанных системах происходит периодическая "перекачка" энергии от одного из тел системы к другому.
Картина биений несколько изменяется, если амплитуды колебаний не равны друг другу. При этом, когда отдельные составляющие результирующего колебания находятся в противофазах, результирующее смещение не обращается в нуль, а будет определяться разностью амплитуд складываемых колебаний.
Пусть складываемые колебания имеют, разные амплитуды, а начальные фазы для простоты рассуждений будем считать одинаковыми: 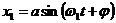 и
и 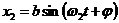 .
.
Результирующее колебание будем определять по принципу суперпозиции, несколько преобразовав складываемые колебания:
 .(340)
.(340)
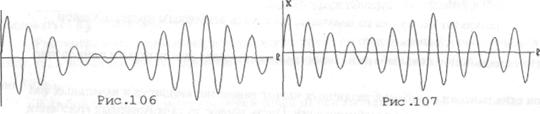
Первые два члена в этом выражении в результате дают биения, характер которых рассмотрен выше. Но с этими биениями складывается чисто гармоническое колебание с амплитудой, равной разности амплитуд складываемых колебаний и с частотой, соответствующей составляющей с большей амплитудой. Таким образом, амплитуда результирующего колебания (биений) не обращается в нуль, а уменьшается только до величины, равной разности амплитуд складываемых колебаний. Примерный вид биений при сложении колебаний с одинаковыми и различными амплитудами приведен на рис.106 и рис.107.





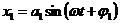 и
и 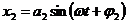

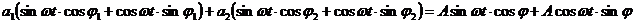

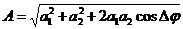 (338)
(338)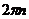 , то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А = а1 + аг если же разность фаз равна (2п + 1)
, то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний А = а1 + аг если же разность фаз равна (2п + 1)  , то - разности амплитуд А = а1-аг. При разности фаз, равной нечётному числу
, то - разности амплитуд А = а1-аг. При разности фаз, равной нечётному числу  амплитуда результирующего колебания равна
амплитуда результирующего колебания равна 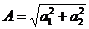 .
. , а второе-
, а второе- 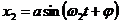 . По принципу суперпозиции колебаний
. По принципу суперпозиции колебаний 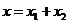 . Используя формулы тригонометрических преобразований, получаем результат в виде:
. Используя формулы тригонометрических преобразований, получаем результат в виде:  (339)
(339)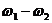 .
.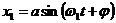 и
и 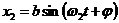 .
. .(340)
.(340)



