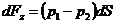Поверхностью уровня называют такую поверхность, во всех точках которой давление одинаково (dP=0)

то, с учетом уравнение Эйлера:

для поверхности уровня:
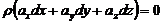
В случае идеальной жидкости:

Пример:
Пусть жидкость покоится в поле тяготения 3емли.
Плоскость 0XY горизонтальна, а ось z направлена вертикально вверх. В этом случае:

Тогда:
 т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.
т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.
ЗАКОН ПАСКАЛЯ
Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:
 (282)
(282)
 (283)
(283)
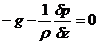 (284)
(284)
С учетом (282) и (283) последнее уравнение (284) принимает вид:
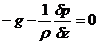 (285)
(285)
откуда:
 (286)
(286)
где  удельный вес жидкости. Интегрируя (286), получаем
удельный вес жидкости. Интегрируя (286), получаем
 (287)
(287)
Постоянная интегрирования будет определена, если в точке с координатой z0 известно давление p0. Тогда


Последнее выражение обычно записывают в виде:
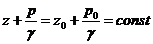 (288) т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.
(288) т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.
СООБЩАЮЩИЕСЯ СОСУДЫ ЗАПОЛНЕНЫ ОДНОРОДНОЙ ЖИДКОСТЬЮ
Свободные поверхности в левом и правом коленах находятся на уровнях Z1 и Z2, а давление на этих поверхностях равно атмосферному Рa. Сравним свободные поверхности с общей для обоих сосудов частью, уровнем Z0, на котором давление равно P0, как показано на рис. 71.


Откуда:

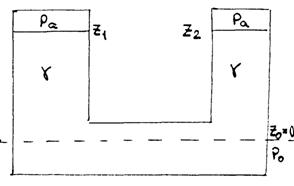
(рис. 71)
Следовательно, свободные поверхности устанавливаются на одном уровне.
ЗАКОН АРХИМЕДА
Тело погружено в жидкость (рис. 73).
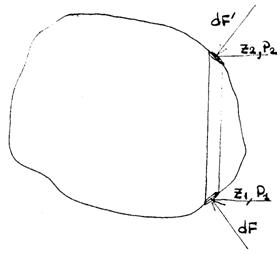
Рис.73.
На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и нижнюю грани этого объема действуют силы давления:

Равнодействующая сил давления в проекции на вертикальную ось равна:
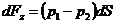
где: dS - проекция dS1 (или dS2) на горизонтальную плоскость. Разность давлений по закону Паскаля равна

где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна

где dV - величина выделенного объема.
Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегрирования предыдущего выражения:

т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом.
Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом, и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность.
Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы. Действительно, поскольку сила Архимеда обусловлена действием распределенных по поверхности сил давления со стороны жидкости, то и равнодействующая сил давления должна быть приложена к смоченной поверхности тела (но не к центру масс вытесненной жидкости, как это часто утверждается). Кроме того, наличие в плавающем теле деформаций можно объяснить только при таком рассмотрении силы Архимеда.







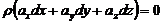


 т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.
т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны. (282)
(282) (283)
(283)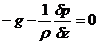 (284)
(284) (286)
(286) удельный вес жидкости. Интегрируя (286), получаем
удельный вес жидкости. Интегрируя (286), получаем (287)
(287)

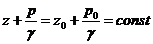 (288) т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.
(288) т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.