Ламинарнре и турбулентное течение жидкости. Число Рейнольдса.

Ламинарным называют упорядоченное, слоистое течение жидкости. Моделью такого течения является относительное движение звеньев телескопической антенны. Ламинарное течение возможно в жидкостях при относительно малых скоростях потока, если же скорость потока увеличивать, то в нем возникают вихри. Когда вихри занимают весь объем потока, последний называется вихревым или турбулентным. Образование вихрей связано с взаимодействием частиц слоев жидкости и переносом импульса из слоя в слой. Переносу содействуют силы инерции, а препятствуют - силы вязкого тре­ния. Поэтому критерием перехода от ламинарного течения к турбу­лентному может служить отношение этих сил. В общем случае, не­зависимо от формы потока, следует рассматривать некоторые харак­теристические параметры потока, например, характеристические размеры и т.д. Силу вязкого трения можно выражать из закона Ньютона для вязкого трения, а силу инерции - по определению:

(301)

Полученное выражение называется числом (критерием) Рейнольдса. Вводя понятие кинематической вязкости, число Рейнольдса можно записать и так:

(302)

где - кинематическая вязкость жидкости.

ФОРМУЛА ПУАЗЕЙЛЯ

(рис. 80)

 

Формула Пуазейля дает величину объемного расхода жидкости при ламинарном течении жидкости по цилиндрическим трубам. Рассмотрим установившийся поток жидкости по цилиндрической трубе радиуса R и длины L, ось которой горизонтальна (рис.80). давление в левом сечении трубы равно P₁, а в правом Р₂, причем P₁>P₂. Скорость потока максимальна вдоль оси трубы и равна ну ли у стенок, выделим в трубе тонкий цилиндрический слой радиуса х и толщины dx, в пределах которого скорость жидкости можно считать одинаковой. На торцы выделенного слоя действует силы давления, равнодействующая которых равна:

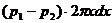
На внутреннюю и внешнюю поверхности слоя действуют силы вязкого трения. По закону Ньютона для вязкого трения на внутреннюю поверхность слоя действует сила:

а равнодействующая сил вязкого трения, приложенных к внутренней и внешней поверхностям, соответственно равна:

Так как жидкость движется с постоянной скоростью, сумма приложенных к слою сил равна нулю, т.е.:

(303)

Интегрируя (303), получим:

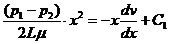
Постоянную интегрирования С₁ можно получить из условия, что вдоль оси трубы скорость максимальна:

следовательно С₁=0. С учетом этого:

(304)

Интегрируя (304), получим:

 

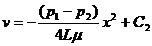
Постоянную интегрирования С₂ получим из условия, что у стенок трубы скорость жидкости равна нулю x=R,, V=0, поэтому:

Подставив найденное значение постоянной интегрирования в общее решение, получим зависимость скорости жидкости от расстояния до оси трубы:

(305)

Для определения объемного расхода запишем сначала элементарный объемный расход по выделенному цилиндрическому слою:

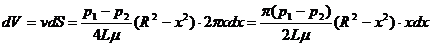(306)

Полный объемный расход по всей трубе получим интегрированием (306) по всем слоям:

(307)

Выражение (287) называет формулой Пуазейля.

 

 

43.1КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Колебательными называются процессы, при которых параметры, характеризующие состояние колебательной системы, обладают опре­делённой повторяемостью во времени. Такими процессами, например, могут являться суточные и годовые колебания температуры атмо­сферы и поверхности Земли, колебания маятников и т.д.

Если про­межутки времени, через которые состояние системы повторяется, равны между собой, то колебания называются периодическими, а про­межуток времени между двумя последовательными одинаковыми состояниями системы – периодом колебаний.

Для периодических колебаний функция, определяющая состояние колеблющейся системы, повторя­ется через период колебаний:

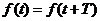
Среди периодических колебаний особое место занимают коле­бания гармонические, т.е. колебания, при которых характеристики движения системы изменяются по гармоническому закону, например:

(308)

Наибольшее внимание, уделяемое в теории колебаний именно часто встречающимся на практике гармоническим процессам, объяс­няется как тем, что для них наиболее хорошо развит аналитический аппарат, так и тем, что любые периодические колебания (и не толь­ко периодические) могут быть рассмотрены в виде определённой комбинации гармонических составляющих. В силу этих причин далее будут рассмотрены преимущественно гармонические колебания. В аналитическом выражении гармонических колебаний (308) ве­личина x отклонения материальной точки от положения равно­весия называется смещением.

Очевидно, что максимальное отклонение точки от положения равновесия равно a, эта величина называется амплитудой колебаний. Физическая величина, равная:

и определяющая состояние колеблющейся системы в данный момент вре­мени, называется фазой колебаний. Значение фазы в момент начала от счёта времени

называется начальной фазой колебаний. Величина w в выражении фазы колебаний, определяющая быстроту колебательного процесса, называется его круговой или циклической частотой колебаний.

Состояние движения при периодических колебаниях должно повторяться через промежутки времени, равные периоду колебаний T. При этом, очевидно, фаза колебаний должна изменятся на 2p (период гармонической функции), т.е.:

Отсюда следует, что период колебаний и циклическая частота связаны между собой соотношением:

Скорость точки, закон движения которой определяется (301), также изменяется по гармоническому закону

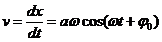(309)

Отметим, что смещение и скорость точки неодновременно обращаются в нуль или принимают максимальные значения, т.е. смешение и скорость отличаются по фазе.

Аналогично получаем, что ускорение точки равно:

(310)

Из выражения для ускорения видно, что оно смещено по фазе относительно смещения и скорости. Хотя смешение и ускорение одновременно проходят через нуль, в этот момент времени они имеют противоположные направления, т.е. смещены на p. Графики зависимостей смещения, скорости и ускорения от времени при гармонических колебаниях представлены условном масштабе на рис.81.

Рис.81

Рисю81

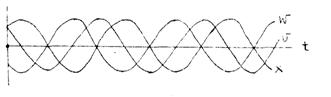
Циклическая частота колебаний и период определяются внутренними параметрами системы, а амплитуда колебаний и начальная фаза - начальными условиями; при этом под начальными условиями понимают значения смещения, и скорости материальной точки в момент начала отсчёта времени:

Из закона гармонического движения (308), пользуясь формулами тригонометрических преобразований, можно записать:

Обозначив и выражение закона движения можно представить в виде

(311)

Выражение (311) показывает, что гармоническое колебание с произвольной начальной фазой, отличной от нуля, можно предста­вить в виде суммы двух гармонических колебаний с нулевыми на­чальными фазами, происходящих по законам синуса и косинуса, при соответствующем подборе амплитуд составляющих.

Начальные условия, как было отмечено выше, определяются значениями смещения и скорости в момент начала отсчёта времени

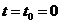
(312)

Из начальных условий, представленных в виде (312), легко определяются значения амплитуды и начальной фазы колебаний:

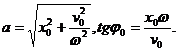(313)

Пояснить влияние начальных условий на характер последу­ющих колебаний системы можно на двух простых частных примерах. В первом случае будем полагать, что в начальный момент времени тело (например, тело маятника) вывели из положения равновесия, сообщив ему отклонение А, и без толчка отпустили. Начальные условия для такого случая имеют вид:

 

Подставив значения начальных смещения и скорости в (313), получим:

Таким образом, при заданных начальных условиях колебания тела будут происходить без начальной фазы по закону косинуса с амплитудой, равной начальному отклонению тела от положения равновесия.

Если же, во втором случае, в исходный момент времени те­лу в положении равновесия (начальное отклонение отсутствует) толчком сообщили скорость, то начальные значения смещения и скорости равны . Подставив эти значения в (313) получаем:

Следовательно, и в этом случае колебания происходят без начальной фазы (начальная фаза равна нулю), но на этот раз по закону синуса с амплитудой, равной .

Важными характеристиками колебательного движения являются их форма, периодичность и т.д. Эти характеристики, независимо от природы колебаний, присущи как колебаниям механическим, так и электрическим, тепловым. Что же касается причин, вызы­вающих и обусловливающих колебания, то они определяются приро­дой колебательной системы. Далее будем рассматривать механи­ческие колебательные системы, например, колебания системы при выводе её из положения равновесия при наличии внутренних упругих взаимодействий. Такие колебания системы, выведенной из положе­ния равновесия, я затем предоставленной самой себе, называют­ся свободными. Характер свободных колебаний зависит от того, насколько большим будет сопротивление движению. Если таковым можно пренебречь, то колебания можно считать чисто гармоническими, с неизменной амплитудой, а при наличии трения амплитуда колебаний будет с течением времени уменьшаться по определённому закону, и колебания нельзя представить только гармонической функцией. В первом случае колебания обычно называют собствен­ными, во втором - затухающими.

 

Собственные колебания

Основные особенности собственных колебаний рассмотрим на примере механической колебательной системы с одной степенью свободы, т.е. такой системы, положение которой можно в любой момент времени определять только одной координатой. Будем счи­тать, что размеры тела достаточно малы, чтобы его можно было рассматривать как материальную точку. Предположим, что при выводе тела из положения равновесия на него будут действовать силы, пропорциональные смещению и направленные противоположно этому смещению -kx. Как говори­лось выше, трением, сопротивлением среды можно пренебречь. Внутренние же силы, величина и направление которых определя­ются смещением из положения равновесия, могут быть, например, силами упругости или силами другой природы, но изменяющимися так же, как и упругие . Такие силы, независимо от их природы, будем называть 'квазиупругими'. С учётом этих сил дифференциальное уравнение движения принимает вид

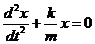(314)

Решением дифференциального уравнения движения (314) имеет вид гармонической функции

(315)

Строгое доказательство этого даёт теория дифференциаль­ных уравнений, мы же легко можем убедиться в справедливости этого утверждения путём подстановки решения (315) в уравнение(314)

 

Как видно, равенство будет соблюдаться для любого момен­та времени, если:

Действительно, отношение 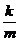можно представить в виде квадрата некоторой величины, поскольку масса тела, коэффициент упругости и, следовательно, само отношение положительны. Как коэффициент k, так и масса тела являются внутренними парамет­рами колебательной системы, поэтому циклическая частота коле­баний w не зависит от начальных условий. От начальных условий зависит только амплитуда колебаний и начальная фаза, которые можно найти из начальных условий, как это было показано ранее. Скорость и ускорение тела при собственных колебаниях так­же изменяются по гармоническому закону:

 

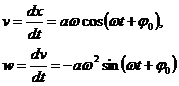
Затухающие колебания

Выясним теперь характер колебаний рассмотренной системы при наличии трения. При этом будем полагать, что силы трения пропорциональны скорости тела и противоположно ей направлены. Такими силами, например, являются силы вязкого трения при до­статочно малых скоростях движения тела. Если тело выведено из положения равновесия на величину x и при этом имеет скорость , то на него будут действовать квазиупругая сила F=-kx и сила сопротивления движению , где, m - коэффициент сопротивления. По второму закону динамики напишем дифференциаль­ное уравнение движения

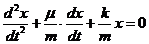
Введём обозначения и 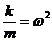. C учётом этих обозначений дифференциальное уравнение принимает вид

(316)

Строгое решение этого уравнения рассматривается в теории дифференциальных уравнений. Это же решение можно получить, исходя из следующих соображений. Во-первых, наличие квазиупру­гих сил свидетельствует о том, что в системе, выведенной из положения равновесия, должны возникнуть колебания. Во-вторых, наличие сил сопротивления движению приводит к тому, что энер­гия колебательной системы и, следовательно, амплитуда колебаний с течением времени должны уменьшаться, кроме того, сопро­тивление среды, тормозя движение тела, влияет на быстроту ко­лебаний, т.е. циклическая частота колебаний может зависеть от сопротивления среды. Исходя из сказанного, решение уравнения (316) будем искать в виде

(317)

Если выражение (317) действительно является решением урав­нения (316), то после подстановки (317) в (316) мы должны получить тождество:

 

Очевидно, тождество будет выполняться для любого произ­вольного момента времени, если будут выполняться следующие условия

(318)

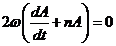(319)

Из условия (319) получаем дифференциальное уравнение для определения амплитуды колебаний

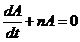
Разделяя переменные, получаем уравнение, удобное для ин­тегрирования

Решением этого уравнения является функция ,

где А₀ - постоянная интегрирования, которую можно определить из начальных условий. Подставив найденное значение амплитуды колебаний в условие (318), получаем:

т.е. частота колебаний действительно отличается от частоты собственных колебаний и равна:

Период колебаний соответственно равен:

С учётом полученных результатов решение исходного диффе­ренциального уравнения движения записывается в виде:

(320)

Это и есть закон колебаний при наличии вязкого трения. Такие колебания называются затухающими.

Скорость и ускорение колебаний тела при наличии вязкого трения определяются соотношениями (321)

(322)

Рассмотренные колебания являются периодическими (все параметры движения изменяются по периодическому закону). В то же время затухающие колебания нельзя назвать гармоническими. Об этом свидетельствует уже зависимость от времени амплитуды колебаний. К тому же выводу приводит и более подробный анализ периодичности изменения отдельных параметров движения, например смещения и скорости. Действительно, из выражений для смещения и скорости сле­дует, что моменты времени, соответствующие прохождению телом положения равновесия, отвечают условию:

а моменты обращения в нуль скорости тела – условию:

Из этих условий следует, что прохождение телом положения равновесия и обращение в нуль скорости тела происходит с оди­наковым периодом. Однако промежутки времени между прохожде­нием положения равновесия и последующим обращением в нуль ско­рости тела не равны четверти периода, как это имеет место при гармонических колебаниях. Следовательно, и по этой причине затухающие колебания не могут быть гармоническими. Степень "негармоничности" затухающих колебаний определяется величиной коэффициента m.

Таким образом, в рассмотренном случае затухания колебаний амплитуда убывает с течением времени по геометрической прогрес­сии. Быстрота затухания колебаний определяется величиной по­терь энергии колебаний (величиной коэффициента сопротивления движению). Кроме того, с увеличением коэффициента сопротивления уменьшается не только амплитуда колебаний, но и частота, а пе­риод колебаний, соответственно, увеличивается. Следует также отметить, что колебания не могут продолжаться бесконечно дол­го, как это можно было бы предположить из закона колебаний. Дело в том, что когда амплитуда колебаний становится беско­нечно малой, малыми будут и упругие силы. При определённых ус­ловиях они не смогут преодолеть сопротивления движению и ко­лебания прекратятся. При достаточно больших коэффициентах со­противления среды процесс затухания колебаний вплоть до полного их прекращения протекает очень быстро. Может получиться, что система не сможет совершить даже одного полного колебания.

Такие колебания называют апериодическими. На практике же коле­бания считают прекратившимися при уменьшении амплитуды колеба­ний до некоторой заданной доли начального значения амплитуды (обычно до 1%). Графически затухающие колебания и апериодически процесс представлены на рис. 82 и рис.83. 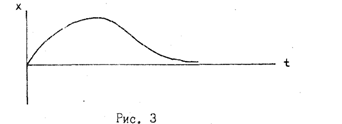При колебаниях системы в вязкой среде, когда силы сопро­тивления движению пропорциональны первой степени скорости, амплитуда колебаний убывает с течением времени по геомет­рической прогрессии, а отношение амплитуд колебаний, отстоящих друг от друга ни один период колебаний, остаётся с тече­нием времени постоянным и равным:

Таким образом, величину этого отношения можно взять в ка­честве характеристики затухания колебаний, её называют декре­ментом затухания. Натуральный логарифм этого отношения (назы­вается логарифмическим декрементом затухания)

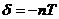(323)

Эту важную характеристику затухающих колебаний на прак­тике берут по абсолютному значению, без учёта его знака. Знак "-" физически означает, что с течением времени амплитуда коле­баний уменьшается.

В реальных механических колебательных системах затухание стремятся свести к минимуму, затухание при этом становится настолько малым, что уменьшением амплитуды колебаний за один период можно пренебречь. Уменьшение амплитуды становится за­метным только через достаточно большой промежуток времени.

Все полученные количественные результаты относительно рассмотренных затухающих колебании справедливы только при на­личии вязкого трения. Если же в системе на колеблющееся тело действуют силы сухого трения, то при сохранении качественных выводов (например, амплитуда колебаний с течением времени уменьшается) количественные характеристики будут иными, будет иным и сам характер изменения амплитуды) колебаний.

Вынужденные колебания

Вынужденными называются колебания системы, возникающие под воздействием внешней силы. Характер этих колебаний опре­деляется как свойствами самой колебательной системы, так и внешней силой. Основные особенности вынужденных колебаний рассмотрим на примере уже известной колебательной системы при условии, что на колеблющееся тело кроме сил упругости и вязкого трения действует ещё внешняя периодическая сила, изме­няющаяся по гармоническому закону:

По основному закону динамики можно составить дифференциаль­ное уравнение движения:

(324)

Здесь, как и ранее:

и .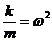

Правая часть уравнения (324), не содержащая искомой пе­ременной х, отлична от нуля. Такие уравнения называются не­однородными (или уравнениями с правой частью). Как известно из теории дифференциальных уравнений, решение неоднородного уравнения можно представить в виде суммы общего решения одно­родного уравнения, соответствующего данному неоднородному, и какого-либо частного решения всего неоднородного уравнения в целом. Однородное уравнение, соответствующее данному неодно­родному, получим, если правую часть уравнения (324) положить равной нулю, т.е. получим дифференциальное уравнение затуха­ющих колебаний, решение которого уже найдено. Что же касает­ся частного решения всего неоднородного уравнения в целом, то оно может быть представлено гармонической функцией, изменяю­щейся с той же частотой, что и сама внешняя сила. При частоте вынуждающей силы, равной нулю, т.е. при действии постоянной внешней силы, тело отклоняется от положения равновесия и, когда сила упругости уравновесит внешнюю силу, движение прекратится. При бесконечно большой частоте вынуждающей силы тело, обладая массой (инертностью), не успевает получить заметное сме­щение за период колебаний. При промежуточных значениях частота амплитуда отлична от нуля, следовательно, амплитуда зависит от частоты вынуждающей силы. По том же соображениям фаза ко­лебаний тела также должна зависеть от частоты вынуждающей силы и отличаться от фазы самой силы.

Первой частью решения уравнения (324) для однородного уравнения (затухающие колебания) через достаточно большой проме­жуток времени можно пренебречь. Поэтому мы будем рассматривать только вторую часть решения, т.е. частное решение уравнения (324) в виде гармонической функции.

Если гармоническая функция действительно является решение всего неоднородного уравнения, то после её подстановки в урав­нение мы должны получить тождество

Как легко заметить, тождество будет выполняться при соб­людении следующих условий:

(325)

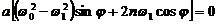(326)

Из условия (326) получаем выражение для начальной фазы:

(327)

Возводя в квадрат и складывая (325) и (325), получим выражение для амплитуды колебаний

(328)

Выражения (327) и (328) показывают, что и начальная фаза колебаний, и их амплитуда зависят от частоты вынуждающей силы. При этом амплитуда при бесконечно большой частоте обращается в нуль, а при постоянной силе (w₁=0) принимает некоторое по­стоянное значение, численно равное отклонению от положения рав­новесия. Имеет смысл более подробно изучить зависимость амп­литуды колебаний от частоты. Очевидно, что экстремальные зна­чения амплитуда будет принимать в тех случаях, когда экстре­мальным будет подкоренное выражение в знаменателе дроби. Для экстремальных значений подкоренного выражения производная от него по частоте должна обращаться в нуль:

Приведенному условию соответствует два значения частоты колебаний:

Чтобы определить, прикаких значениях частоты само под­коренное выражение принимает максимальное или минимальное зна­чение, надо определить знак второй производной при указанных значениях частоты. Вторая производная от подкоренного выраже­ния по частоте равна

После подстановки найденных значений частоты в выражение второй производной получаем:

Учитывая, что в реальных механических колебательных сис­темах вязкость среды по отношению к собственной частоте мала, получаем, что при подстановке первого значения частоты вторая производная принимает отрицательное значение, а при подстанов­ке второго - положительное. Это означает, что первое значение частоты соответствует минимуму амплитуды колебаний, а второе - максимуму.

Явление возрастания амплитуды колебаний при некоторых значениях частоты вынуждающей силы называется резонансом. Со­ответствующее значение частоты: называется резонансной частотой. Резонансная амплитуда колебаний принимает значение:

(329)

а соответствующее значение начальной фазы колебаний (смещение по фазе самих колебаний относительно вынуждающей силы:

(330)

Как видно из выражений (329) и (330), при отсутствии трения (n = 0) амплитуда колебаний обращается в бесконечность, а ко­лебание относительно вынуждающей силы смещено по фазе на p/2.

В реальных механических колебательных системах вязкость среды хотя и мала, но всё же не равна нулю. Поэтому амплиту­да колебаний при резонансе принимает конечные значения, тем меньшие, чем больше коэффициент вязкости. На рис.84 представ­лены резонансные амплитудные характеристики, т.е. зависимости амплитуды колебаний от частоты вынуждающей силы при различных значениях вязкости:

Начальная фаза колебаний также зависит от частоты вынуж­дающей силы. Графики зависимости начальной фазы колебания от частоты вынуждающей силы, называемые фазовыми резонансными кривыми, для различных значений вязкости приведены на рис.85.

Из полученных результатов не совсем очевидным является то, что при резонансе колебание относительно вынуждающей силы сме­щено по фазе на p/2. На первый взгляд кажется, что смещение и вынудающая сила должны совпадать по фазе. На самом деле работа силы будет положительной (увеличивать энергию колебаний) в том случае, если сила будет совпадать по фазе не со смеще­нием, а со скоростью. В противном случае на отдельных участках траектории сила будет направлена против движения тела и уменьшать его скорость и, соответственно, максимальное смещение.

 

 

МАТЕМАТИЧЕСКИЙ маятник

Маятником обычно называют твёрдое тело, способное под действием приложенных сил совершать колебания относительно какого-либо центра или оси. Если тип маятника специально не оговорен, то считается, что маятник совершает колебания под действием силы тяжести.

Простейший маятник представляет собой небольшое массивное тело, подвешенное на нити или укреплённое на конце лёгкого стержня длины l. Если по условиям эксперимента нить можно считать невесомой и нерастяжимой, а размерами тела можно пре­небречь по сравнению с длиной нити, то маятник можно рассмат­ривать как материальную точку, находящуюся на неизменном рас­стоянии от точки подвеса. Такой маятник называется математи­ческим. На практике приведенные выше условия являются трудно выполнимыми, тело нельзя считать материальной точкой, и маятник называют в этом случае физическим.

Закон движения математического маятника можно получить из основного закона динамики для вращательного движения. Пред­положим, что масса тела равна m, длина нити l, а разме­рами тела по сравнению с длиной нити можно пренебречь. Если тело маятника отклонить от положения равновесия на малый угол a <= 5°, то это положение не будет устойчивым, и маятник на­чинает движение. Относительно точки подвеса O (рис. 86) момент силы натяжения нити равен 0, поскольку линия действия силы тяжести проходит через точку подвеса.

Момент же силы тяжести относительно точки подвеса отличен от нуля и равен m . Поскольку при малых углах можно считать , то выражение момента силы тяжести окончательны можно записать как . Знак '-' означает, что направление момента силы тяжести противоположно угловому отклонению маятника. Момент инерции для материальной точки равен . С учётом ска­занного основной закон динамики для маятника принимает вид:

Приведем дифференциальное уравнение к форме:

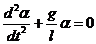(333)

Отметим, что это уравнение является уравнением гармонических колебаний. Решением его является гармоническая функция . Циклическая частота, определяемая выражением , зависит от свойств самого маятника. Так как период колебаний связан с циклической частотой, то и его значение также определяется па­раметрами маятника и не зависит от начальных условий:

 

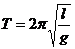
Отметим также, что как само дифференциальное уравнение движения, так и его решение получены в предположении, что уг­ловые отклонения маятника от положения равновесия малы. Если же угловые амплитуды будут больше указанной величины, то реше­ние дифференциального уравнения 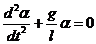не даст такой простой гармонической формы. Колебания не будут гармони­ческими.

Закон движения математического маятника можно представить и в несколько ином виде. Предположим, что отклонение тела маятника от положения равновесия по горизонтали равно x. Дифференциальное уравнение движения тела маятника запишем по второму закону динамики в проекциях на горизонтальное направление. Проекцию равнодействующей силы на горизонтальное направление можно определить как . При малых отклонениях выполняется условие Поэтому , где знак "-" означает, что горизонтальная проекция равнодействующей силы направлена противоположно смещению l. С учётом сказанного дифференциальное уравнение движения можно представить в виде

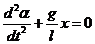
Уравнение, как видно, также представляет собой дифференциальное уравнение гармонических колебаний, решением которого является гармоническая функция x=x₀*sin(wt+j). Таким обра­зом, линейные отклонения тела маятника от положения равновесия также изменяются по гармоническому закону с той же циклической частотой

Пружинные маятники

Пружинные маятники представляют собой тела, укреплённые на упругих пружинах. При этом упругостью самого тела и массой пружины пренебрегают.

В зависимости от способа крепления маятника и предоставляемой ему свободы перемещения его перемещение может про­исходить только под действием силы упругости (горизонтально расположенный маятник) или под действием сил упруго­сти и силы тяжести тела маятника при вертикальном расположении маятника. На рис.87 представлены оба маятника.

Рассмотрим сначала горизонтальный пружинный маятник. Если телу маятника сообщить отклонение от положения равновесия x, то на него будет действовать сила упругости пружины, пропорциональная при малых отклонениях пер­вой степени смещения и противоположно ему направленная. Под действием этой силы и будет происходить дальнейшее движение тела маятника. По второму закону динамики дифференциальное урав­нение движения принимает вид:

Т.е. является уравнением гармонических колебаний, решением которого является гармоническая функция:

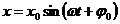
Циклическая частота равна 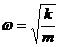, а период, соответственно,

Таким образом, период колебаний (циклическая частота) опреде­ляется параметрами маятника, что же касается амплитуды коле и начальной фазы, то они, как было сказано ранее, определяются из начальных условий.

При вертикальном расположении маятника на характер движения тела будет оказывать влияние не только сила упругости пружины, но я сила тяжести тела. При отклонении тела от положения равновесия на x, на него будут действовать сила упруго­сти и сила тяжести. При малых отклонениях сила упругости пропорциональна первой степени смещения и противоположно ему направлена 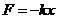. По второму закону динамики запишем дифференциальное уравнение движения:

или

В отличии от предыдущего случая правая часть уравнения не равна нулю, уравнение является неоднородным. Решением такого уравнения будем искать в виде . После подстановки искомого решения в уравнение движения полу­чаем тождество:

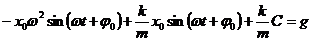
Как видно тождество выполняется при условии, что .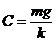

Легко убедиться, что дополнительный постоянный член в решении означает смещение тела маятника в положении равновесия под дей­ствием силы тяжести.