Для более наглядного представления различного рода движений, в том числе и гармонических, применяются графические способы их описания. Среди этих способов мы рассмотрим только самые распространённые.
 а) Временные диаграммы
а) Временные диаграммы


Наиболее широко применяемыми и известными являются временные (плоские) диаграммы, на которых в зависимости от времени представляются параметры движения, например, смещение, скорость и ускорение. Если материальная точка совершает движение по гармоническому закону  , то скорость её в произвольный момент времени выражается соотношением
, то скорость её в произвольный момент времени выражается соотношением  , а ускорение, соответственно,
, а ускорение, соответственно, 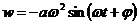 . Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения.
. Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения.
б) векторные диаграммы

Часто употребляемыми являются также так называемые векторные диаграммы. Они широко применяются при изучении гармонических колебаний, при изучении сложения колебаний и т.д. Любое гармоническое колебание можно представить следующим образом. Пусть начало некоторого вектора совпадает с началом координат (рис. 99), а сам он вращается вокруг начала координат с угловой скоростью, численно равной циклической частоте колебаний. Как видно из рисунка, в любой момент времени проекции вектора на оси координат численно равны

и
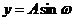
 Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна
Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна  , а ускорение
, а ускорение 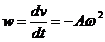 . Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на
. Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на  и
и  , длины которых равны амплитудным значениям скорости и ускорения. Рис.100
, длины которых равны амплитудным значениям скорости и ускорения. Рис.100
Весьма наглядным является сложение гармонических колебаний, представляемое с помощью векторных диаграмм. Предположим, что обе гармонические составляющие имеют одинаковую частоту изменения параметров (т.е. угловые скорости вращения обоих векторов одинаковы). Если начальные фазы составляющих различны, то векторы в пространстве не совпадают по направлению. Геометрическая сумма этих векторов определяет амплитуду результирующего колебания. Действительно, поскольку для гармонических колебаний справедлив принцип суперпозиции, то результирующее смещение, получаемое телом, должно равняться по этому принципу геометрической сумме смещений, получаемых телом за счёт участия в каждом из отдельных колебаний. Так как при одинаковой угловой скорости вращения слагаемых векторов их относительное расположение (рис.100) не будет изменяться с течением времени, то не будет изменяться, соответственно, и длина суммарного вектора (амплитуда результирующего колебания), который будет вращаться с той же угловой скоростью, что и слагаемые векторы. Таким образом, результирующее колебание будет происходить с той же циклической частотой, а его амплитуда численно равна геометрической сумме складываемых векторов.
Если же циклические частоты складываемых колебаний (угловые скорости вращения векторов) неодинаковы, то относительное расположение складываемых векторов с течением времени будет периодически изменяться, будет периодически изменяться и амплитуда результирующего колебания, принимая значения от нуля до величины, равной сумме амплитуд складываемых колебаний. Поскольку периодичность изменения амплитуды результирующего колебания (длины суммарного вектора) определяется относительной скоростью вращения векторов, то циклическая частота изменения амплитуды результирующего колебания должна определяться разностью циклических частот складываемых колебаний. Более подробно случай сложения одинаково направленных колебаний рассмотрим ниже.
в)Спектральное представление колебаний
 В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.
В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.
В таких случаях на графиках зависимости амплитуды или энергии, пропорциональной амплитуде колебаний, от частоты для соответствующих частот откладываются отрезки, в определенном масштабе равные амплитуде (энергии) колебаний. Спектральная характеристика гармонического колебания частоты w0 представлена на рис. 101.
г) Фазовое представление колебаний
При фазовом представлении колебаний состояние колеблющейся системы описывается в фазовой плоскости. Фазовой плоскостью называют плоскость, координаты точек которой определяют состояние колеблющейся системы с одной степенью свободы. По осям координат откладываются значения координат и скоростей механической системы. При гармонических колебаниях вместо скорости (или импульса) откладывается обычно отношение скорости тела к циклической частоте колебаний. Изменению состояния системы соответствует перемещение точки по фазовой плоскости. Отметим, что на фазовой плоскости можно представить не только колебательный процесс, но и любой Другой вид движения, например, прямолинейное движение, движение тела, брошенного под углом к горизонту и т.д.
| | | | |
| |  |
| | |  |
| |
Рассмотрим фазовые представления некоторых частных случаев движения. На рис. 102 представлено равномерное прямолинейное движение. Действительно, при равномерном и прямолинейном движении на всей траектории (для любой координаты) скорость тела имеет постоянное значение. Этому случаю соответствует прямая, параллельная оси
X на фазовой плоскости.
Рис.102 Рис.103
Если же скорость с течением времени изменяется, то фазовая траектория не будет представлять собой прямую линию. Так, если тело совершает равнозамедленное движение с начальной скоростью  из начала координат, то закон изменения его скорости записывается в виде
из начала координат, то закон изменения его скорости записывается в виде  , а закон движения - в форме
, а закон движения - в форме  . Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости
. Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости  . Этому уравнению соответствует парабола, представленная на рис.103.
. Этому уравнению соответствует парабола, представленная на рис.103.
При гармонических колебаниях закон движения тела можно записать в виде  . Скорость его при этом для произвольного момента времени имеет вид
. Скорость его при этом для произвольного момента времени имеет вид  . Исключая время, получим уравнение фазовой траектории
. Исключая время, получим уравнение фазовой траектории
 , которая представлена на рис.104.
, которая представлена на рис.104.
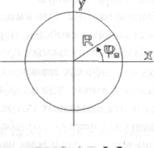

Рис.104 Рис.105
Этими основными видами геометрического представления колебаний и будем пользоваться в дальнейшем.
Рассмотрим также равномерное движение точки по окружности. Радиус вращения равен  ,, в исходный момент времени направление на точку составляло угол
,, в исходный момент времени направление на точку составляло угол  с осью X (рис.105).
с осью X (рис.105).
В любой момент времени проекции точки на оси координат равны  и
и  . Соответствующие проекции скорости на оси координат равны
. Соответствующие проекции скорости на оси координат равны  и
и  . Ускорение же в проекциях на оси координат равно
. Ускорение же в проекциях на оси координат равно  и
и  . Отметим, что такое определение закона движения точки в проекциях на оси координат аналогично уже отмеченному выше векторному представлению колебаний.
. Отметим, что такое определение закона движения точки в проекциях на оси координат аналогично уже отмеченному выше векторному представлению колебаний.
В самом деле, как видно из выражений проекций точки на оси координат, а также проекций векторов скорости её и ускорения, вдоль отдельных координатных направлений точка совершает гармонические колебания. При этом угловая скорость точки численно равна циклической (круговой) частоте колебаний (откуда ясно происхождение названия самой частоты).





 а) Временные диаграммы
а) Временные диаграммы

 , то скорость её в произвольный момент времени выражается соотношением
, то скорость её в произвольный момент времени выражается соотношением  , а ускорение, соответственно,
, а ускорение, соответственно, 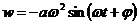 . Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения.
. Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения. Часто употребляемыми являются также так называемые векторные диаграммы. Они широко применяются при изучении гармонических колебаний, при изучении сложения колебаний и т.д. Любое гармоническое колебание можно представить следующим образом. Пусть начало некоторого вектора совпадает с началом координат (рис. 99), а сам он вращается вокруг начала координат с угловой скоростью, численно равной циклической частоте колебаний. Как видно из рисунка, в любой момент времени проекции вектора на оси координат численно равны
Часто употребляемыми являются также так называемые векторные диаграммы. Они широко применяются при изучении гармонических колебаний, при изучении сложения колебаний и т.д. Любое гармоническое колебание можно представить следующим образом. Пусть начало некоторого вектора совпадает с началом координат (рис. 99), а сам он вращается вокруг начала координат с угловой скоростью, численно равной циклической частоте колебаний. Как видно из рисунка, в любой момент времени проекции вектора на оси координат численно равны  и
и 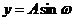
 Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна
Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна  , а ускорение
, а ускорение 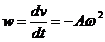 . Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на
. Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на  и
и  , длины которых равны амплитудным значениям скорости и ускорения. Рис.100
, длины которых равны амплитудным значениям скорости и ускорения. Рис.100 В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.
В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.

 из начала координат, то закон изменения его скорости записывается в виде
из начала координат, то закон изменения его скорости записывается в виде  , а закон движения - в форме
, а закон движения - в форме  . Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости
. Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости  . Этому уравнению соответствует парабола, представленная на рис.103.
. Этому уравнению соответствует парабола, представленная на рис.103. , которая представлена на рис.104.
, которая представлена на рис.104.

 ,, в исходный момент времени направление на точку составляло угол
,, в исходный момент времени направление на точку составляло угол  с осью X (рис.105).
с осью X (рис.105). и
и  . Соответствующие проекции скорости на оси координат равны
. Соответствующие проекции скорости на оси координат равны  и
и  . Ускорение же в проекциях на оси координат равно
. Ускорение же в проекциях на оси координат равно  и
и  . Отметим, что такое определение закона движения точки в проекциях на оси координат аналогично уже отмеченному выше векторному представлению колебаний.
. Отметим, что такое определение закона движения точки в проекциях на оси координат аналогично уже отмеченному выше векторному представлению колебаний.


