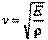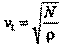Твёрдое тело представляет собой упругую среду,поэтому, вызванные внешним воздействием в какой-либо его точке, деформации должны распространяться по всему объёму тела. Выделим и твёрдом теле такой его участок (см. рис. 133), чтобы во всех точках сечения выделенного участка деформации были одинаковыми. Воздействуем на торец выделенного участка кратковременным импульсом силы F=Δt, нормальным к сечению. Под действием импульса в пограничном слое возникает деформация сжатия. Силы упругости в деформированном слое действуют на частицы слоя, прилегающего к деформированному, в результате чего возникают деформации и в этом слое. Таким образом, импульс сжатия начинает распространяться в теле.
Процесс распространения импульса сжатия можно представить как движение некоторого "избытка массы" Δm=ΔpV, где: Δр - изменение плотности среды в деформированием слое, а V - его объём. По второму закону динамики:
Δ(mv)=FΔt
Упругую силуможно выразить из закона Гука:
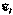 где: - относительная деформация продольных размеров слоя, S - площадь поперечного сечения, Е - модуль Юнга.
где: - относительная деформация продольных размеров слоя, S - площадь поперечного сечения, Е - модуль Юнга.
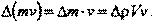 Поскольку скорость распространения импульса сжатия не зависит от начальных условий, а определяется только свойствами самой среды, то изменение импульса деформированного слоя выражается соотношением
Поскольку скорость распространения импульса сжатия не зависит от начальных условий, а определяется только свойствами самой среды, то изменение импульса деформированного слоя выражается соотношением
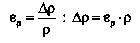 Превышение плотности Δр над плотностью недеформированного участка можно выразить через относительное изменение плотности.
Превышение плотности Δр над плотностью недеформированного участка можно выразить через относительное изменение плотности.
Учтём также, что длина Δl деформированного слоя равна расстоянию, проходимому импульсом сжатия за время действия силы, т.е. Δl = vΔt.
С учетом всего сказанного основной закон динамики принимает вид:
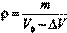
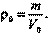
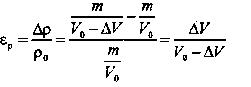
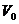 Относительное изменение продольных размеров и относительное изменение плотности при малых деформациях можно считать равными. Действительно, если масса участка среды, подвергаемого деформации, равна т, а объём, то плотность недеформированного участка равна После того, как в слое возникла деформация сжатия, плотность увеличится:, где ΔV=SΔl - изменение объёма слоя. Исходя из сказанного, относительное изменение плотности равно:
Относительное изменение продольных размеров и относительное изменение плотности при малых деформациях можно считать равными. Действительно, если масса участка среды, подвергаемого деформации, равна т, а объём, то плотность недеформированного участка равна После того, как в слое возникла деформация сжатия, плотность увеличится:, где ΔV=SΔl - изменение объёма слоя. Исходя из сказанного, относительное изменение плотности равно:
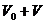 Умножив числитель и знаменатель полученного выражения на разделив затем
Умножив числитель и знаменатель полученного выражения на разделив затем
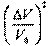
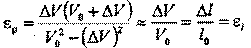 числитель и знаменатель на и пренебрегая величиной второго порядка малости (при малых деформациях), получим, что
числитель и знаменатель на и пренебрегая величиной второго порядка малости (при малых деформациях), получим, что
Таким образом, относительное изменение плотности при малых деформациях равно относительной деформации продольных размеров. Учитывая это, окончательно основной закон динамики приводим к виду:
pv2 =Е
откуда получаем значение скорости распространения продольного импульса деформации:
сли на торец выделенного участка среды воздействуем не импульсом силы, а силой, периодически изменяющейся во времени, то в среде будут распространиться периодические возмущения, т.е. возникнет упругая волна.
Проводя аналогичные рассуждения для случая, когда на торец выделенного участка действует импульс силы по касательной к сечению, получим такие же качественные выводы. В отличие от предыдущего случая в слоях будет возникать деформация сдвига, относительная деформация слоя из закона Гука выражается через модуль сдвига N, а скорость распространения импульса деформации, соответственно, будет равна:
Отметим также, что в первом из рассмотренных случаев колебания частиц среды относительно их положения равновесия происходят вдоль направления распространения возмущения (волны) в среде, а во втором - по нормали к направлению распространения волны. Волны, в которых колебания частиц среды проходят по направлению распространения самой волны, называются продольными. Если же колебания частиц среды происходят по нормали к направлению распространения волны, волна называется поперечной.
Введём несколько определений, касающихся волн.
1. Совокупность точек среды, колеблющихся в одинаковых фазах, называется волновой или фазовой поверхностью.
2. Фронтом волны называется совокупность точек среды, до которых в данный момент времени дошли колебания. Таким образом, фронтом волны является волновая поверхность, соответствующая нулевой фазе колебаний.
3. Фазовой или волновой скоростью называется скорость перемещения в среде постоянной фазы колебаний.
В зависимости от формы фронта волны (волновой поверхности) различает частные типы волн - плоские, сферические, цилиндрические, для которых волновая поверхность представляет собой, соответственно, плоскость, сферическую и цилиндрическую поверхности.





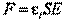
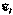 где: - относительная деформация продольных размеров слоя, S - площадь поперечного сечения, Е - модуль Юнга.
где: - относительная деформация продольных размеров слоя, S - площадь поперечного сечения, Е - модуль Юнга.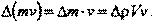 Поскольку скорость распространения импульса сжатия не зависит от начальных условий, а определяется только свойствами самой среды, то изменение импульса деформированного слоя выражается соотношением
Поскольку скорость распространения импульса сжатия не зависит от начальных условий, а определяется только свойствами самой среды, то изменение импульса деформированного слоя выражается соотношением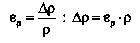 Превышение плотности Δр над плотностью недеформированного участка можно выразить через относительное изменение плотности.
Превышение плотности Δр над плотностью недеформированного участка можно выразить через относительное изменение плотности.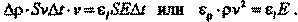
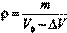
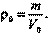
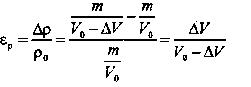
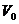 Относительное изменение продольных размеров и относительное изменение плотности при малых деформациях можно считать равными. Действительно, если масса участка среды, подвергаемого деформации, равна т, а объём, то плотность недеформированного участка равна После того, как в слое возникла деформация сжатия, плотность увеличится:, где ΔV=SΔl - изменение объёма слоя. Исходя из сказанного, относительное изменение плотности равно:
Относительное изменение продольных размеров и относительное изменение плотности при малых деформациях можно считать равными. Действительно, если масса участка среды, подвергаемого деформации, равна т, а объём, то плотность недеформированного участка равна После того, как в слое возникла деформация сжатия, плотность увеличится:, где ΔV=SΔl - изменение объёма слоя. Исходя из сказанного, относительное изменение плотности равно: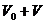 Умножив числитель и знаменатель полученного выражения на разделив затем
Умножив числитель и знаменатель полученного выражения на разделив затем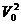
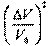
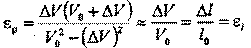 числитель и знаменатель на и пренебрегая величиной второго порядка малости (при малых деформациях), получим, что
числитель и знаменатель на и пренебрегая величиной второго порядка малости (при малых деформациях), получим, что