

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Если на тело действует несколько сил, то каждая из них сообщает телу ускорение, определяемое основным законом динамики, так, как если бы других сил не было.
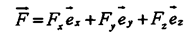 Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):
Например, произвольно направленную и в пространстве силу F можно представить в виде суммы ее составляющих (компонентов):
где ex, ey, ez - орты прямоугольной системы координат OXYz.
Второй закон динамики в этом случае имеет вид:
 |
 |
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОГО ЦЕНТРА.
Моментом силы называют количественную меру вращательного эффекта, вызываемого силой. Момент силы должен определять величину этого эффекта, плоскость поворота точки и направление поворота в этой плоскости.
 (рис23)
(рис23)
Величина момента силы равна произведению модуля силы на ее плечо h (величину перпендикуляра, опущенного из заданного центра O на линию действия силы). Если начало вектора силы совпадает с точкой А, а конец – А с точкой В, то, очевидно, плоскость поворота совпадает с плоскостью треугольника OAB (рис. 23).
 Условились вектор момента силы относительно центра M0(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часовых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен.
Условились вектор момента силы относительно центра M0(F) проводить из этого центра O перпендикулярно плоскости поворота в ту сторону, откуда поворот виден происходящим против хода часовых стрелок. Модуль же вектора (длина вектора в выбранном масштабе) равен.
 |
где: r - радиус-вектор точки приложения силы, проведенный из заданного центра.
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ.
Моментом силы относительно оси называют величину, характеризующую вращательный эффект, вызываемый силой при вращении тела вокруг заданной оси.
К телу А, способному вращаться вокруг оси z приложена сила F (рис. 24). Очевидно, что эффект вызываемый силой, определяется суммой эффектов, вызываемых ее проекциями Fz и Fxy, первая из которых вращения тела вокруг оси z вызвать не может. Следовательно, момент силы относительно заданной оси определяется моментом ее проекции на плоскость, перпендикулярную оси, относительно точки Пересечения оси с плоскостью.
МОМЕНТ СИЛЫ оТНОСИТЕЛЬНО КООРДИНАТНОЙ ОСИ.
Пользуясь полученным выше результатом можно записать выражения моментов силы относительно координатных осей. Пусть к телу приложена сила F, координаты точки приложения которой равны x,y,z. Момент силы F относительно оси oz равен моменту ее проекции Fxy относительно начала координат (т. 0). В свою очередь момент Fxy равен сумме моментов сил Fx и Fy относительно того же центра. Очевидно, что плечи сил Fx и Fy численно равны координатам точки приложения силы y и x соответственно. С учетом знаков моментов этих составляющих можно записать
 (рис 25)
(рис 25)
 |

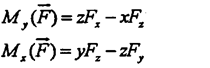 |
 Аналогично определяются моменты силы F относительно осей ОХ и ОУ:
Аналогично определяются моменты силы F относительно осей ОХ и ОУ:|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!