Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).
Свойство 1. Определитель не изменяется при транспонировании, т.е.
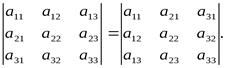
Доказательство.
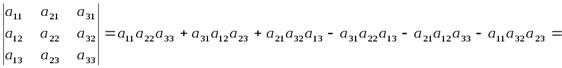
= 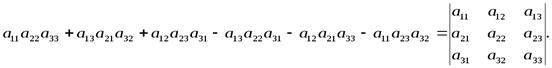
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.
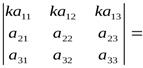
 .
.
Доказательство.
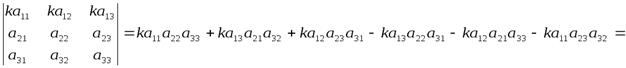



Свойство 3. Определитель, имеющий нулевую строку, равен 0.
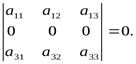
Доказательство этого свойства следует из свойства 2 при k= 0.
Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.

Свойство 5. Определитель, две строки которого пропорциональны, равен 0.
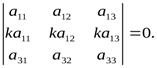
Доказательство следует из свойств 2 и 4.
Свойство 6. При перестановке двух строк определителя он умножается на –1.

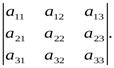
Доказательство.
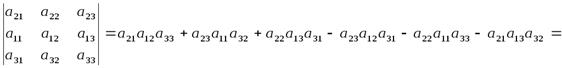
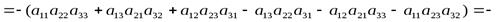

Свойство 7.
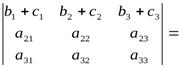


Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.
Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

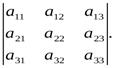
Доказательство следует из свойств 7 и 5.
9. Дать определения предикатов и кванторов.
Предикаты
О п р е д е л е н и е: Функция F (х1, х2,..., хn), определенная на множестве М и принимающая значения из множества {0, 1}, называется n- местным предикатом (n- местной высказывательной формой).
Таким образом, например, F(х) ― это одноместный предикат или одноместная высказывателъная форма, которая становится высказыванием, если вместо переменной х подставить любое значение из некоторого множества М. Любое высказывание является нуль-местным предикатом и обозначается F0.
Итак, в логике предикатов рассматривают символы трех видов, связанные с множеством М и множеством {0, 1}:
а) предметные постоянные а, b, с,..., d ∈M;
б) предметные переменные х, у, z,..., принимающие значения из множества М;
в) переменные высказывания А, В, С, …,принимающие значения из множества {0,1}.
 Если на множестве М задан n- местный предикат
Если на множестве М задан n- местный предикат
F (х1, х2,...., хn), то множество М разбивается на два множества: М=А 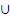 В, на одном из множеств предикат принимает истинное значение, на другом ― ложное. Первое множество А называется множеством истинности предиката.
В, на одном из множеств предикат принимает истинное значение, на другом ― ложное. Первое множество А называется множеством истинности предиката.
На множестве предикатов (высказывательных форм) можно определить отношение равносильности.
О п р е д е л е н и е: Два предиката F(х1, х2,...., хn) и
P(х1, х2,...., хn) от одних и тех же переменных называются равносильными, если они имеют одно и то же множество истинности. Обозначение: F (х1, х2,...., хn)⇔P (х1, х2,...., хn).
Отношение равносильности на множестве предикатов является отношением эквивалентности, так как оно определяется через отношение равенства множеств их истинности, а отношение равенства есть отношение эквивалентности на любом множестве.
С помощью логических операций (&, ∨,...) из данных высказывательных форм можно строить более сложные высказывательные формы.
Однако из предикатов можно получать высказывания и другим путем. Для этого вводятся так называемые операции «навешивания кванторов».
 Пусть одноместный предикат Р(х) задан на множестве М, тогда под символами (
Пусть одноместный предикат Р(х) задан на множестве М, тогда под символами ( х ∈М) Р(х) и (
х ∈М) Р(х) и (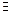 х ∈М) Р(х) понимаем высказывание: «Для любого х ∈M Р(х)» и «существует х ∈М такое, что Р(х)».
х ∈М) Р(х) понимаем высказывание: «Для любого х ∈M Р(х)» и «существует х ∈М такое, что Р(х)».
Слова «для любого х» кратко обозначают символом  х и называют квантором общности по переменной х. Слова «существует такой х, что...» обозначают символом
х и называют квантором общности по переменной х. Слова «существует такой х, что...» обозначают символом  х и называют квантором существования.
х и называют квантором существования.
Высказывание  х ∈М Р (х) считается истинным, если все элементы множества М обладают свойством Р и будет ложным, если найдется хотя бы один элемент, который этим свойством не обладает.
х ∈М Р (х) считается истинным, если все элементы множества М обладают свойством Р и будет ложным, если найдется хотя бы один элемент, который этим свойством не обладает.
Высказывание (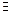 х ∈М) Р(х) считается истинным, если хотя бы один элемент множества М обладает свойством Р и будет ложным, если ни один элемент множества М этим свойством не обладает.
х ∈М) Р(х) считается истинным, если хотя бы один элемент множества М обладает свойством Р и будет ложным, если ни один элемент множества М этим свойством не обладает.
Квантор существования обобщает логическую операцию «дизъюнкция» на бесконечном множестве.





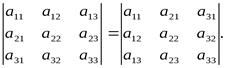
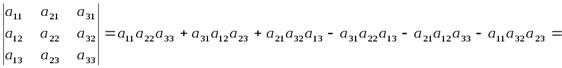
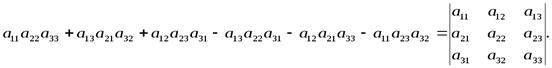
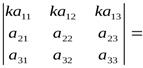
 .
.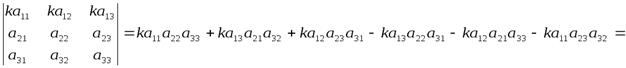



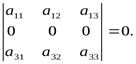


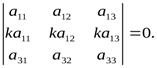

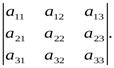
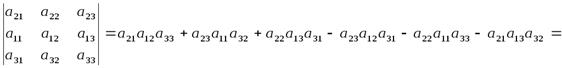
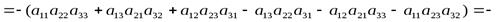

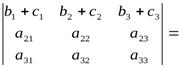



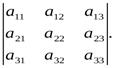
 Если на множестве М задан n- местный предикат
Если на множестве М задан n- местный предикат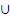 В, на одном из множеств предикат принимает истинное значение, на другом ― ложное. Первое множество А называется множеством истинности предиката.
В, на одном из множеств предикат принимает истинное значение, на другом ― ложное. Первое множество А называется множеством истинности предиката. Пусть одноместный предикат Р(х) задан на множестве М, тогда под символами (
Пусть одноместный предикат Р(х) задан на множестве М, тогда под символами ( х ∈М) Р(х) и (
х ∈М) Р(х) и ( х ∈М) Р(х) понимаем высказывание: «Для любого х ∈M Р(х)» и «существует х ∈М такое, что Р(х)».
х ∈М) Р(х) понимаем высказывание: «Для любого х ∈M Р(х)» и «существует х ∈М такое, что Р(х)». х и называют квантором существования.
х и называют квантором существования.


