Определение. Комплексным числомz=x+iy называется упорядоченная пара действительных чисел 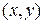 :
:  .
.
Действительные числа х и у называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются: 
Определение. Вещественное неотрицательное число:

называют модулем комплексного числа  .
.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть  , где
, где  и
и  , где
, где 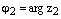 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
 .
.
Теорема. (Свойства модуля комплексного числа.)
Пусть  – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
– произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1)  и
и  . Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
. Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2) расстояниемеждуточками  и
и  комплексной плоскости равно модулю разности соответствующих комплексных чисел:
комплексной плоскости равно модулю разности соответствующих комплексных чисел:  ;
;
3)  ;
;
4)  ;
;
Доказательство. 1) По предыдущей теореме имеем:

 , где
, где  и
и  ,
,
т.е. 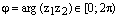 .
.
Таким образом, равенства  и
и  есть тригонометрическаяформа записи числа
есть тригонометрическаяформа записи числа 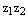 , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем
, следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем  , ч.т.д.
, ч.т.д.
Далее, т.к.  , то по только что доказанному свойству
, то по только что доказанному свойству  , ч.т.д.
, ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплекснойплоскости изображаются точками симметричными относительно начала координат. Действительно, пусть  . Тогда
. Тогда  и точки
и точки  ,
,  имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.
имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.  , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
, ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
2). Пусть  ,
,  . Тогда
. Тогда  и по формуле (12) имеем:
и по формуле (12) имеем:
 . (14)
. (14)
С другой стороны, рассмотрим числа  и
и  как точки на комплексной плоскости. Тогда точка
как точки на комплексной плоскости. Тогда точка  имеет декартовыекоординаты
имеет декартовыекоординаты  , а
, а  и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплекснойплоскости точки  ,
,  и начало координат О. В общем случае эти три точки являются вершинами треугольника
и начало координат О. В общем случае эти три точки являются вершинами треугольника  :
:

рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны 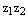 этого треугольника равна
этого треугольника равна  , а длины сторон
, а длины сторон  и
и  равны по определению модулям чисел
равны по определению модулям чисел  и
и  :
:  ,
,  . Отсюда и получаем, что
. Отсюда и получаем, что 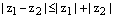 .
.
Заменим в последнем неравенстве число  на противоположное число
на противоположное число  , тогда получаем:
, тогда получаем:
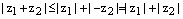 , ч.т.д.
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О,  и
и  лежат на одной прямой.
лежат на одной прямой.
4)  , откуда следует
, откуда следует
 . Поменяв местами
. Поменяв местами  и
и  , получаем
, получаем
 , откуда и следует доказываемое неравенство.
, откуда и следует доказываемое неравенство.
Теорема доказана.





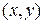 :
:  .
.

 , где
, где  и
и  , где
, где 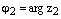 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда .
. – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
– произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда: и
и  . Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
. Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны; и
и  комплексной плоскости равно модулю разности соответствующих комплексных чисел:
комплексной плоскости равно модулю разности соответствующих комплексных чисел:  ;
; ;
; ;
;
 , где
, где  и
и  ,
,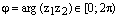 .
. и
и  есть тригонометрическаяформа записи числа
есть тригонометрическаяформа записи числа 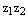 , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем
, следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем  , то по только что доказанному свойству
, то по только что доказанному свойству  , ч.т.д.
, ч.т.д. . Тогда
. Тогда  и точки
и точки  ,
,  имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.
имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.  ,
,  . Тогда
. Тогда  и по формуле (12) имеем:
и по формуле (12) имеем: . (14)
. (14) , а
, а  и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д. :
:
 и
и  равны по определению модулям чисел
равны по определению модулям чисел  ,
,  . Отсюда и получаем, что
. Отсюда и получаем, что 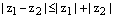 .
. , тогда получаем:
, тогда получаем: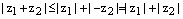 , ч.т.д.
, ч.т.д. , откуда следует
, откуда следует . Поменяв местами
. Поменяв местами  , откуда и следует доказываемое неравенство.
, откуда и следует доказываемое неравенство.


