Предложения, образованные из других предложений с помощью логических связок, называют составными или сложными. Предложения, которые не содержат логических связок, называют элементарными или простыми.
1. Отрицание – единственная операция, которая может применяться к одному высказыванию.
Отрицанием высказывания называется новое высказывание, которое истинно тогда и только тогда, когда само высказывание ложно и ложно, когда само высказывание истинно.
Отрицание обозначается  , или b, читается: «не А» или «неверно, что А».
, или b, читается: «не А» или «неверно, что А».
Для произвольного высказывания А определение удобно записывать с помощью так называемой таблицы истинности:
| А
| 
|
|
|
|
|
|
|
2.Конъюнкция (логическое умножение).
Конъюнкцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны.
Конъюнкция обозначается 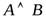 или А&B; читается: «А и В».
или А&B; читается: «А и В».
Таблица истинности для конъюнкции выглядит следующим образом:
| А
| В
| 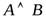
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Дизъюнкция (логическое сложение).
Дизъюнкцией двух высказываний является новое высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция обозначается 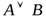 и читается «А или В».
и читается «А или В».
Таблица истинности для дизъюнкции выглядит следующим образом:
| А
| В
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Импликация (логическое следствие).
Импликацией двух высказываний называется новое высказывание, которое ложно тогда и только тогда, когда первое высказывание истинно, а второе – ложно.
Импликация обозначается  или
или 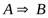 , читается «Если А, то В» («Когда А, тогда В», «А, следовательно В»).
, читается «Если А, то В» («Когда А, тогда В», «А, следовательно В»).
Таблица истинности импликации выглядит так:
| А
| В
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Компоненты импликации имеют свои собственные «имена»: предложение А называется посылкой или антецедентом, предложение В – заключением или консеквентом.
Принятое определение импликации соответствует употреблению союза «если…, то…» не только в математике, но и в обыденной, повседневной речи. Так, например, обращение приятеля «Если будет хорошая погода, то я приду к тебе в гости» вы расцените как ложь в том и только в том случае, если погода будет хорошая, а приятель к вам в гости не придет.
5. Эквиваленция (логическая равносильность).
Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания одновременно истинны либо ложны.
Эквиваленция обозначается  или
или 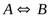 , читается «А тогда и только тогда, когда В».
, читается «А тогда и только тогда, когда В».
Таблица истинности для эквиваленции выглядит так:
| А
| В
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В форме эквиваленции, как правило, формулируются определения (например, определения логических операций).
3. Дать определения функции, композиции функций и указать их свойства.
Определение.
Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению  ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение  .
.
Для указания этого факта, что y есть функция от х, пишут:  ,
, 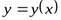 ,
,  и т.п.
и т.п.
Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так 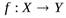 (рис.1.1).
(рис.1.1).
 Рис. 1.1
Рис. 1.1
Переменная х называется независимой переменной или аргументом.
Переменная y называется зависимой переменной или функцией.
Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.
Область определения и изменения функции
Определение.
Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения или областью существования этой функции.
Определение.
Множество Х называется областью определения функции и обозначается 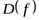 .
.
Определение.
Множество значений Y называется областью изменения или областью значений функции, и обозначается  .
.
Область изменения функции (множество ее значений) определяется законом соответствия.
Определение.
Функция 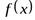 называется числовой функцией, если ее область определения
называется числовой функцией, если ее область определения 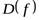 и множество значений
и множество значений  содержатся в множестве действительных чисел R.
содержатся в множестве действительных чисел R.
В дальнейшем будем изучать лишь числовые функции. Частное значение функции 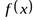 при
при  записывается так:
записывается так: 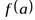 .
.
Характеризуют функцию по следующим свойствам:
- четность или нечетность функции;
- периодичность функции;
- нули функции;
- возрастание или убывание функции (монотонность функции);
- ограниченность функции.
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция  называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.
называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.  .
.
График четной функции расположен симметрично относительно оси  .
.
Определение.
Функция  называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е.
называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е. 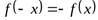 .
.
График нечетной функции расположен симметрично относительно начала координат.
Функция может быть ни четной ни нечетной, и в этом случае её называют функцией общего вида.
Графики таких функций не симметричны ни относительно оси  , ни относительно начала координат.
, ни относительно начала координат.
Периодические функции
Определение.
Функция  называется периодической, если существует такое положительное число
называется периодической, если существует такое положительное число  , что
, что  в области определения функции.
в области определения функции.
Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции  .
.
Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль,  , называется нулем функции.
, называется нулем функции.
Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции.
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция  называется ограниченной на множестве Х, если существует такое число
называется ограниченной на множестве Х, если существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.
Например, функции 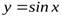 и
и 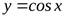 – ограниченные функции, т.к.
– ограниченные функции, т.к. 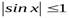 и
и 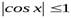 для
для  .
.
График ограниченной функции лежит между прямыми  и
и 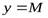 .
.
Пусть даны числовые функции f(x) и g(x), такие, что E(f) ⊂ UD(g). Их композицией называется новая числовая функция F, заданная на D(f), которая каждому x ∈ D(f) ставит в соответствие число g[f(x)]. Функцию F обозначают также: g○ f:
(g ○ f) (x) = g(f(x))
Если функции f(x) и g(x) заданы своими выражениями, то для получения выражения композиции этих функций надо подставить в выражение функции g(x) вместо x выражение функции f(x).
Свойства композиции
Композиция ассоциативна:
 .
.
Если  — тождественное отображение на
— тождественное отображение на  , то есть
, то есть
 ,
,
то
 .
.
Если  — тождественное отображение на
— тождественное отображение на  , то есть
, то есть
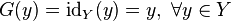 ,
,
то
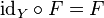 .
.
Рассмотрим пространство всех биекций множества  на себя и обозначим его
на себя и обозначим его  . То есть если
. То есть если 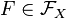 , то
, то  — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из  является бинарной операцией, а
является бинарной операцией, а  — группой.
— группой. 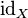 является нейтральным элементом этой группы. Обратным к элементу
является нейтральным элементом этой группы. Обратным к элементу 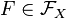 является
является 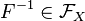 — обратная функция.
— обратная функция.
Группа  , вообще говоря, не коммутативна, то есть
, вообще говоря, не коммутативна, то есть  .
.





 , или b, читается: «не А» или «неверно, что А».
, или b, читается: «не А» или «неверно, что А».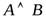 или А&B; читается: «А и В».
или А&B; читается: «А и В».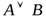 и читается «А или В».
и читается «А или В».
 или
или 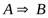 , читается «Если А, то В» («Когда А, тогда В», «А, следовательно В»).
, читается «Если А, то В» («Когда А, тогда В», «А, следовательно В»).
 или
или 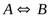 , читается «А тогда и только тогда, когда В».
, читается «А тогда и только тогда, когда В».
 ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение  .
. ,
, 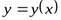 ,
,  и т.п.
и т.п.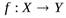 (рис.1.1).
(рис.1.1). Рис. 1.1
Рис. 1.1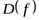 .
. .
.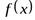 называется числовой функцией, если ее область определения
называется числовой функцией, если ее область определения 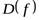 и множество значений
и множество значений 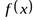 при
при  записывается так:
записывается так: 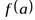 .
. называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.
называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.  .
. .
.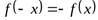 .
. , что
, что  в области определения функции.
в области определения функции. , называется нулем функции.
, называется нулем функции. , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.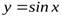 и
и 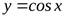 – ограниченные функции, т.к.
– ограниченные функции, т.к. 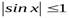 и
и 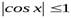 для
для  .
. и
и 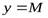 .
. .
. — тождественное отображение на
— тождественное отображение на  , то есть
, то есть ,
, .
. — тождественное отображение на
— тождественное отображение на  , то есть
, то есть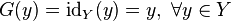 ,
,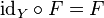 .
. . То есть если
. То есть если 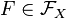 , то
, то  — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из  — группой.
— группой. 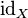 является нейтральным элементом этой группы. Обратным к элементу
является нейтральным элементом этой группы. Обратным к элементу 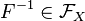 — обратная функция.
— обратная функция. .
.


