

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Кванторы применяются для того, чтобы перейти от высказывательной формы к истинному высказыванию, эта операция называется квантификацией.
Квантификация - переход от высказывательной формы к истинному высказыванию.
Рассмотрим двуместную высказывательную форму  и всевозможные варианты её квантификации:
и всевозможные варианты её квантификации:
(1) 
(2) 
(3) 
(4) 
(5) 
(6) 
(7) 
(8) 
(1) ≡ (2)
(3) ≡ (4)
Одноименные кванторы можно менять местами
(6) => (5)
(8) => (7)
Если высказывательная форма зависит от n переменных, то при квантификации высказывательной формы по xi переменной, xi переменная становится связанной (связана квантором), при этом все остальные называются свободными.
Чтобы перейти от высказывательной формы  к истинному высказыванию нужно проквантифицировать её n раз по каждой переменной.
к истинному высказыванию нужно проквантифицировать её n раз по каждой переменной.
Отрицание предложений кванторами.
Рассмотрим такой пример: 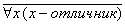 (отрицание предложения необходимо начинать со слов <неверно, что:>) - <неверно, что все ученики отличники>. Попытаемся перефразировать: <среди учеников есть хотя бы неотличник> или
(отрицание предложения необходимо начинать со слов <неверно, что:>) - <неверно, что все ученики отличники>. Попытаемся перефразировать: <среди учеников есть хотя бы неотличник> или  , т. е.
, т. е.  ≡
≡ 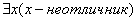 . Ещё один пример:
. Ещё один пример:  ≡
≡  .
.
Правила построения отрицания предложения с кванторами:
- каждый квантор меняем на противоположный;
- отрицание переносим на высказывательную форму.
Пример: Предложение: <в каждой стране найдётся город, у всех жителей которого глаза одинакового цвета>.
Запись кванторами:  (глаза одинакового цвета)
(глаза одинакового цвета)
Отрицание кванторами:  (неверно, что глаза одинакового цвета)
(неверно, что глаза одинакового цвета)
Отрицание предложение: <существует страна, в каждом городе которой найдётся житель с глазами разного цвета>.
Дать определение кванторов, свободных и связанных переменных.
Кванторы – логические символы или специальные обозначения для некоторых часто встречающихся выражений.
Например: 1) Квантор общности –  – любой, каков бы ни был.
– любой, каков бы ни был.
 – для всех x истинно (или выполнимо) свойство p (x).
– для всех x истинно (или выполнимо) свойство p (x).
2) Квантор существования –  – существует.
– существует.
 – найдутся (или существуют) x, обладающие свойством p (x).
– найдутся (или существуют) x, обладающие свойством p (x).
Свободные и связанные переменные
Множество свободных переменных * формулы F определяется рекурсивно, следующим образом:
Определение 1 (Свободные переменные).
Определение 2 (Замкнутая формула). Формула без свободных переменных называется замкнутой формулой, или предложением.
|
|
Определение 3 (Связаная переменная). Переменная v связана в формуле F, если F содержит вхождение Kv, где K – квантор.
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!