Определение. Максимальная линейно независимая подсистема S’ системы векторов S называется базисом системы S.
Ранее было доказано, что всякая максимально линейно независимая подсистема n-мерного пространства состоит из n векторов. Отсюда можно сделать выводы:
1) базис любой системы векторов пространства Rn всегда содержит не более чем n векторов;
2) в любой системе векторов может содержаться несколько базисов, однако число векторов в каждом базисе одно и тоже;
3) любой базис пространства Rn содержит n векторов;
4) любая линейно независимая система из n векторов является базисом пространства Rn.
Из всех доказанных выше результатов можно сделать следующие выводы:
1) в n-мерном пространстве всякая линейно независимая система, состоящая из n векторов, будет максимальной;
2) любая максимальная линейно независимая система векторов этого пространства состоит не более чем из n векторов;
3) всякая линейно независимая система n-мерных векторов содержится хотя бы в одной максимальной линейно независимой системе;
4) в n-мерном пространстве существует бесконечно много различных максимально линейно независимых систем векторов.
Определение. Число векторов, входящих в любую максимальную линейно независимую подсистему данной системы векторов, называется рангом этой системы векторов.
Теорема. Система векторов  является базисом линейного пространства
является базисом линейного пространства 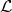 тогда и только тогда, когда это максимальная линейно независимая система векторов.
тогда и только тогда, когда это максимальная линейно независимая система векторов.
Доказательство. 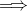
Пусть  — базис
— базис 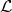 . Тогда по определению
. Тогда по определению  — линейно независимая система векторов. Любой вектор представим в виде линейной комбинации
— линейно независимая система векторов. Любой вектор представим в виде линейной комбинации  , т.е. любая большая система векторов линейно зависима, т.е. для векторов
, т.е. любая большая система векторов линейно зависима, т.е. для векторов 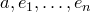
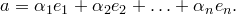
Значит, базис — максимальная линейно независимая система.
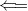
Пусть  — максимальная линейно независимая система. Второе свойство базиса выполняется. Любая большая система векторов линейно зависима:
— максимальная линейно независимая система. Второе свойство базиса выполняется. Любая большая система векторов линейно зависима:

т.е. каждый вектор является линейной комбинацией векторов этой системы — выполнено первое свойство.
Теорема (о ранге системы векторов). Ранг системы векторов не изменится, если к ней добавить (или удалить) вектор, являющийся линейной комбинацией остальных.
Сформулировать и доказать критерий совместности системы линейных уравнений.
Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Теорема Кронекера-Капелли.
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.
Доказательство теоремы.
Необходимость. Система 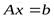 совместна. Докажем, что
совместна. Докажем, что 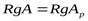 .
.
Система 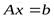 совместна — существуют такие числа
совместна — существуют такие числа 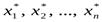 ,что
,что

т.е. вектор-столбец правой части линейно выражается через столбцы 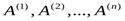 матрицы A. Это означает, что при добавлении столбца
матрицы A. Это означает, что при добавлении столбца 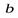 число линейно независимых столбцов не увеличивается, т.е.
число линейно независимых столбцов не увеличивается, т.е. 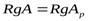 . Необходимость доказана.
. Необходимость доказана.
Достаточность. 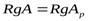 . Докажем, что система
. Докажем, что система 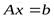 совместна.
совместна.
Пусть 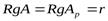 . Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов
. Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов  . Тогда столбцы
. Тогда столбцы 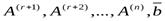 — линейно зависимы и, следовательно, столбец
— линейно зависимы и, следовательно, столбец 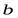 линейно выражается через
линейно выражается через 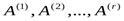 :
:  .
.
Положим 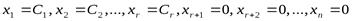 ,
,
тогда
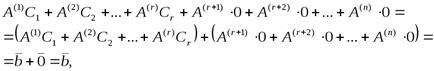
т.е. вектор 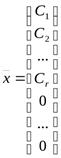 — решение системы
— решение системы  ,
,
т.е. система  совместна. Теорема доказана.
совместна. Теорема доказана.





 является базисом линейного пространства
является базисом линейного пространства 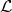 тогда и только тогда, когда это максимальная линейно независимая система векторов.
тогда и только тогда, когда это максимальная линейно независимая система векторов.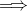
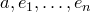
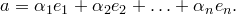
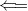

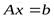 совместна. Докажем, что
совместна. Докажем, что 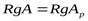 .
.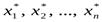 ,что
,что
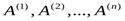 матрицы A. Это означает, что при добавлении столбца
матрицы A. Это означает, что при добавлении столбца 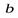 число линейно независимых столбцов не увеличивается, т.е.
число линейно независимых столбцов не увеличивается, т.е. 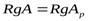 . Необходимость доказана.
. Необходимость доказана.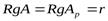 . Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов
. Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов  . Тогда столбцы
. Тогда столбцы 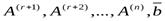 — линейно зависимы и, следовательно, столбец
— линейно зависимы и, следовательно, столбец 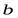 линейно выражается через
линейно выражается через 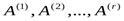 :
:  .
.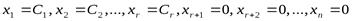 ,
,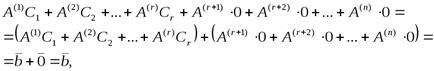
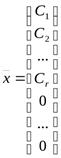 — решение системы
— решение системы  ,
,


