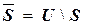Под множеством понимается любая (конечная или бесконечная) совокупность объектов с некоторой общей характеристикой (или, что то же самое - объектов одинаковой природы). Эти объекты называются элементами множества. Множества с конечным числом различных элементов могут быть описаны путем явного перечисления всех этих элементов: обычно, эти элементы заключаются в фигурные скобки. Например, 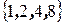 - множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами
- множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами
N - множество натуральных чисел
Z - множество целых чисел
Q - множество рациональных чисел
R - множество вещественных (или действительных) чисел
При заданном множестве S включение 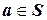 указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут
указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут 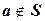 (или
(или  ).
).
Множество можно описать, указав свойство, присущее только элементам именно этого множества. Множество всех объектов, обладающих свойством  , обозначают через
, обозначают через  . Например:
. Например: 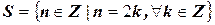 - множество всех четных чисел;
- множество всех четных чисел; 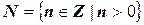 - множество натуральных чисел.
- множество натуральных чисел.
Множество, не содержащее элементов, называется пустым и его принято обозначать символом Æ.
Говорят, что S – подмножество множества  или
или  (
(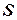 содержится в
содержится в  ), если все элементы множества
), если все элементы множества 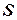 являются также элементами множества
являются также элементами множества  , то есть
, то есть
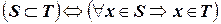 .
.
Два множества 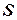 и
и  совпадают (или равны), если у них одни и те же элементы. Символически это выглядит так:
совпадают (или равны), если у них одни и те же элементы. Символически это выглядит так:
 и
и  .
.
Заметим, что пустое множество Æ (т.е. множество совсем не содержащее элементов) по определению входит в число подмножеств любого множества.
Если  , но
, но 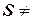 Æ и
Æ и  , то
, то 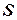 - называется собственным подмножеством в
- называется собственным подмножеством в  . Для выделения подмножества
. Для выделения подмножества  часто используют какое - либо свойство, присущее только элементам из
часто используют какое - либо свойство, присущее только элементам из 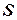 .
.
Для множеств  справедливы следующие соотношения:
справедливы следующие соотношения:
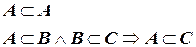
(значок 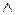 - это значок конъюнкции, т. е. логическое «и»).
- это значок конъюнкции, т. е. логическое «и»).
Конечное множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до  .
.
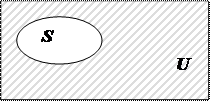
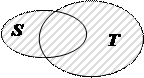
Для пояснения некоторых определений и свойств операций над множествами и различных соотношений между ними воспользуемся диаграммами Эйлера – Венна, на которых множества, подлежащие рассмотрению, изображаются в виде совокупности точек на плоскости.
Универса́льное мно́жество — в математике множество, содержащее все объекты и все множества.
Универсальное множество обычно обозначается {\displaystyle U} 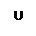 (от англ. universe, universal set), реже {\displaystyle E}
(от англ. universe, universal set), реже {\displaystyle E}  .
.
На диаграммах Венна универсальное множество (в обоих значениях) изображается множеством точек некоторого прямоугольника; подмножества его точек изображают подмножества универсального множества[1].
Пусть В  А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В:
А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В: 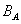 '.= {x | x
'.= {x | x 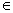 A, x
A, x 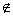 B}.
B}.
7. Дать определения операций над множествами: объединение, пересечение, разность.
1. Под пересечением (произведение) двух множеств 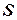 и
и  понимается множество:
понимается множество:
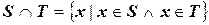
Например:
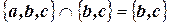
2. Под объединением (сумма) двух множеств 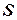 и
и  понимается множество:
понимается множество:

(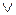 - значок дизъюнкции, логическое «или»)
- значок дизъюнкции, логическое «или»)
Например:
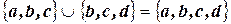
3. Разностью 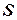 \
\  множеств
множеств 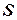 и
и  называется совокупность тех элементов, из
называется совокупность тех элементов, из 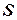 , которые не содержатся в
, которые не содержатся в  , то есть
, то есть
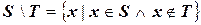
Порядок множеств при выполнении этой операции существенен.
4. Если 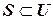 (здесь
(здесь 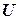 – основное, универсальное множество) то
– основное, универсальное множество) то 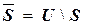





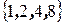 - множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами
- множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами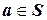 указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут
указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут 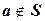 (или
(или  ).
). , обозначают через
, обозначают через  . Например:
. Например: 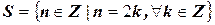 - множество всех четных чисел;
- множество всех четных чисел; 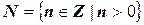 - множество натуральных чисел.
- множество натуральных чисел. или
или  (
(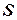 содержится в
содержится в 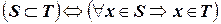 .
. и
и  .
.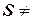 Æ и
Æ и  , то
, то  справедливы следующие соотношения:
справедливы следующие соотношения: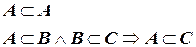
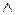 - это значок конъюнкции, т. е. логическое «и»).
- это значок конъюнкции, т. е. логическое «и»). .
.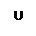 (от англ. universe, universal set), реже {\displaystyle E}
(от англ. universe, universal set), реже {\displaystyle E}  .
. А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В:
А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В: 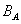 '.= {x | x
'.= {x | x 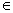 A, x
A, x 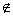 B}.
B}.
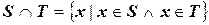
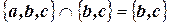

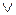 - значок дизъюнкции, логическое «или»)
- значок дизъюнкции, логическое «или»)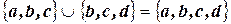

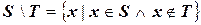
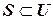 (здесь
(здесь 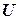 – основное, универсальное множество) то
– основное, универсальное множество) то