Задачи линейного программирования

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

; (5.2)

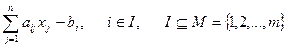; (5.3)

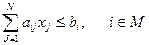; (5.4)

. (5.5)

При этом система линейных уравнений (5.3) и неравенств (5.4), (5.5), определяющая допустимое множество решений задачи W, на­зывается системой ограничений задачи линейного программирования, а линейная функция f(X) называется целевой функцией или критери­ем оптимальности.

В частном случае, если 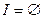, то система (5.3) - (5.4) состоит только из линейных неравенств, а если I=M, то – из линейных уравнений.

Если математическая модель задачи линейного программирова­ния имеет вид:

; (5.6)

; (5.7)

, (5.8)

то говорят, что задача представлена в канонической форме.

Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ог­раничениям равенств и заменять переменные, которые не подчи­няются условию неотрицательности. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот.

Правило приведения задачи линейного программирования к канони­ческому виду состоит в следующем:

1) если в исходной задаче требуется определить максимум ли­нейной функции, то следует изменить знак и искать минимум этой функции;

2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на –1;

3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобра­зуются в равенства;

4) если некоторая переменная х_k не имеет ограничений по зна­ку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными:

, где l – свободный индекс, .

Пример 5.1. Приведение к канонической форме задачи линейного программирования:

Решение. Введем в каждое уравнение системы ограничений выравниваю­щие переменные х₄, х₅, x ₆. Система запишется в виде равенств, причем в первое и третье уравнения системы ограничений пере­менные х₄, x₆ вводятся в левую часть со знаком «+», а во второе уравнение вводится х₅ со знаком «–».

Итак:

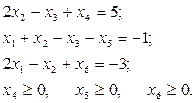
Свободные члены в канонической форме должны быть поло­жительными, для этого два последних уравнения умножим на – 1:

В канонической форме записи задач линейного программиро­вания все переменные, входящие в систему ограничений, должны быть неотрицательными. Допустим, что

где .

Подставляя данное выражение в систему ограничений и в целе­вую функцию и записывая переменные в порядке возрастания ин­декса, получим задачу линейного программирования, представлен­ную в канонической форме:

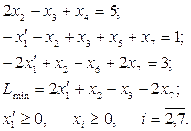
Примеры построения экономико-математических моделей задач линейного программирования

Рассмотрим процесс построения математических моделей задач линейного программирования на примерах.

Пример 5.2. Определение оптимального ассортимента продукции.

Предприятие изготавливает два вида продукции – П₁, и П₂, ко­торая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные за­пасы сырья в сутки составляют 9 и 13 единиц соответственно. Рас­ход сырья на единицу продукции вида П₁ и вида П₂ дан в табл. 5.1.

Таблица 5.1. Расход сырья продукции

Сырье	Рас ход сырья на 1 ед. продукции	Запас сырья, ед.
П1	П2
А
В

 

Опыт работы показал, что суточный спрос на продукцию П₁ никогда не превышает спроса на продукцию П₂ более чем на 1 ед. Кроме того, известно, что спрос на продукцию П₂ никогда не пре­вышает 2 ед. в сутки.

Оптовые цены единицы продукции равны: 3 д. е. – для П₁ и 4 д. е. для П₂.

Какое количество продукции каждого вида должно произво­дить предприятие, чтобы доход от реализации продукции был мак­симальным?

Процесс построения математической модели для решения по­ставленной задачи начинается с ответов на следующие вопроса (Таха Х. Введение в исследование операций: В 2-х кн. – М.: Мир, 1985.).

1. Для определения каких величин должна быть построена мо­дель, т. е. как идентифицировать переменные данной задачи?

2. Какие ограничения должны быть наложены на переменные,
чтобы выполнялись условия, характерные для моделируемой сис­темы?

3. В чем состоит цель задачи, для достижения которой из всех
допустимых значений переменных нужно выбрать те, которые бу­дут соответствовать оптимальному (наилучшему) решению задачи?

Ответы на вышеперечисленные вопросы могут быть сформули­рованы для данной задачи так: фирме требуется определить объе­мы производства каждого вида продукции в тоннах, максимизиру­ющие доход в д. е. от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов.

Для построения математической модели остается только иден­тифицировать переменные и представить цель и ограничения в ви­де математических функций этих переменных.

Предположим, что предприятие изготовит x₁ единиц продукции П₁ и х₂ единиц продукции П₂. Поскольку производство продукции П₁ и П₂ ограничено имеющимися в распоряжении предприятия сы­рьем каждого вида и спросом на данную продукцию, а также учи­тывая, что количество изготовляемых изделий не может быть отри­цательным, должны выполняться следующие неравенства:

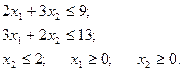
Доход от реализации х_х единиц продукции П₁ и х₂ единиц про­дукции П₂ составит .

Таким образом, мы приходим к следующей математической за­даче: среди всех неотрицательных решений данной системы линей­ных неравенств требуется найти такое, при котором функция F принимает максимальное значения F_max.

Рассмотренная задача относится к разряду типовых задач опти­мизации производственной программы предприятия. В качестве критериев оптимальности в этих задачах могут быть также исполь­зованы: прибыль, себестоимость, номенклатура производимой про­дукции и затраты станочного времени.

Пример 5.3. Использование мощностей оборудования.

Предприятие имеет т моделей машин различных мощностей. Задан план по времени и номенклатуре: Т – время работы каждой машины; продукции j- го вида должно быть выпущено не менее N_j единиц.

Необходимо составить такой план работы оборудования, чтобы обеспечить минимальные затраты на производство, если известны производительность каждой i- й машины по выпуску j -го вида про­дукции b_ij и стоимость единицы времени, затрачиваемого i -й ма­шиной на выпуск j -го вида продукции с_ij.

Другими словами, задача для предприятия состоит в следую­щем: требуется определить время работы i- й машины по выпуску j -го вида продукции х_ij, обеспечивающее минимальные затраты на производство при соблюдении ограничений по общему времени работы машин Т и заданному количеству продукции N_j.

По условию задачи машины работают заданное время Т, поэто­му данное ограничение можно представить в следующем виде:

. (5.9)

Ограничение по заданному количеству продукции выглядит следующим образом:

. (510)

Задача решается на минимум затрат на производство:

. (5.11)

Необходимо также учесть неотрицательность переменных .

Задача поставлена так, чтобы израсходовать все отведенное время работы машины, т. е. обеспечить полную загрузку машины. При этом количество выпускаемой продукции каждого вида должно быть по крайней мере не менее N_j. Однако в некоторых случаях не допускается превышение плана по номенклатуре, тогда ограничения математической модели изменяются следующим образом:

. (5.12)

. (5. 13)

. (5.14)

 

Пример 5.4. Минимизация дисбаланса на линии сборки.

Промышленная фирма производит изделие, представляющее собой сборку из m различных узлов. Эти узлы изготавливаются на n заводах.

Из-за различий в составе технологического оборудования производительность заводов по выпуску j -го узла неодинакова и равна . Каждый i -ый завод располагает максимальным суммарным ресурсом времени в течение недели для производства m узлов, равного Величине T_i.

Задача состоит в максимизации выпуска изделий, что по существу эквивалентно минимизации дисбаланса, возникающего вследствие некомплектности поставки по одному или по нескольким видам узлов.

В данной задаче требуется определить еженедельные затрать времени (в часах) на производство j -го узла на i- м заводе, не превышающие в сумме временные ресурсы i -го завода и обеспечиваю­щие максимальный выпуск изделий.

Пусть x_ij – недельный фонд времени (в часах), выделяемый на заводе i для производства узла j. Тогда объемы производства узла j будут следующими:

. (5. 15)

Так как в конечной сборке каждый из комплектующих узлов представлен в одном экземпляре, количество конечных изделий должно быть равно количеству комплектующих узлов, объем про­изводства которых минимален:

. (5 16)

 

Условие рассматриваемой задачи устанавливает ограничение на фонд времени, которым располагает завод i.

Таким образом, математическая модель может быть представ­лена в следующем виде.

Максимизируем

. (5. 17)

. (5.18)

для всех i и j.

Эта модель не является линейной, но ее можно привести к ли­нейной форме с помощью простого преобразования. Пусть Y – ко­личество изделий:

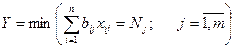. (5. 19)

Этому выражению с математической точки зрения эквивалент­на следующая формулировка: максимизировать Z = Y при ограни­чениях

. (5. 20)

. (5.21)

для всех i и j;

 

Пример 5.5. Задача составления кормовой смеси, или задача о диете (Вентцель Е. С, Овчаров Л. А. Прикладные задачи теории вероятнос­тей. - М.: Радио и связь, 1983).

Пусть крупная фирма (условно назовем ее «Суперрацион») име­ет возможность покупать т различных видов сырья и приготавли­вать различные виды смесей (продуктов). Каждый вид сырья содер­жит разное количество питательных компонентов (ингредиентов).

Лабораторией фирмы установлено, что продукция должна удов­летворять по крайней мере некоторым минимальным требованиям с точки зрения питательности (полезности). Перед руководством фирмы стоит задача определить количество каждого i -го сырья, об­разующего смесь минимальной стоимости при соблюдении требо­ваний к общему расходу смеси и ее питательности.

Решение

Введем условные обозначения:

x_i – количество /-го сырья в смеси;

т – количество видов сырья;

п – количество ингредиентов в сырье;

а_ij – количество ингредиента j, содержащегося в единице i -го вида сырья;

b_ij – минимальное количество ингредиента/, содержащегося в единице смеси;

с_i - стоимость единицы сырья i;

q — минимальный общий вес смеси, используемый фирмой.

Задача может быть представлена в виде

. (5. 22)

при следующих ограничениях:

на общий расход смеси:

; (5. 23)

на питательность смеси:

; (5. 24)

на неотрицательность переменных:

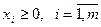. (5.25)

 

Пример 5.6. Задача составления жидких смесей.

Еще один класс моделей, аналогичных рассмотренным выше, возникает при решении экономической проблемы, связанной с из готовлением смесей различных жидкостей с целью получения поль­зующихся спросом готовых продуктов.

Представим себе фирму, торгующую различного рода химичес­кими продуктами, каждый из которых является смесью нескольких компонентов. Предположим, что эта фирма планирует изготовле­ние смесей m видов. Обозначим подлежащее определению количе­ство литров i -го химического компонента, используемого для полу­чения j -го продукта через х_ij. Будем предполагать, что

.

Первая группа ограничений относится к объемам потребляе­мых химических компонентов:

. (5.26)

где S_i – объем i -го химического компонента, которым располагает фирма в начале планируемого периода.

Вторая группа ограничений отражает требование, заключающе­еся в том, чтобы запланированный выпуск продукции хотя бы в минимальной степени удовлетворял имеющийся спрос на каждый из химических продуктов, т. е.

. (5.27)

где D_j – минимальный спрос на продукцию у в течение планируемого пе­риода.

Третья группа ограничений связана с технологическими осо­бенностями, которые необходимо принимать во внимание при при­готовлении смеси например, простое ограничение, определяемое некоторыми минимально допустимыми значениями, отношения между объемами двух химических компонентов в процессе получе­ния продукта j:

или .

где r – некоторая заданная константа.

Обозначив через Р_ij доход с единицы продукции x_ij, запишем целевую функцию:

. (5.28)

Пример 5.7. Задача о раскрое или о минимизации обрезков.

Данная задача состоит в разработке таких технологических пла­нов раскроя, при которых получается необходимый комплекс заго­товок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму.

Например, продукция бумажной фирмы выпускается в виде бу­мажных рулонов стандартной ширины L. По специальным заказам потребителей фирма поставляет рулоны других размеров, для этого производится разрезание стандартных рулонов. Типичные заказы на рулоны нестандартных размеров могут включать т видов шири­ной . Известна потребность в нестандартных рулонах каждого вида, она равна l_i. Возможны n различных вариантов по­строения технологической карты раскроя рулонов стандартной ши­рины L на рулоны длиной l_i.

Обозначим через a_ij количество рулонов i -го вида, получаемых при раскрое единицы стандартного рулона по j -му варианту. При каждом варианте раскроя на каждый стандартный рулон возможны потери, равные Р_j. К потерям следует относить также избыточные рулоны нестандартной длины l_i, получаемые при различных вари­антах раскроя .

В качестве переменных следует идентифицировать количество стандартных рулонов, которые должны быть разрезаны при j -м ва­рианте раскроя. Определим переменную следующим образом: x_j количество стандартных рулонов, разрезаемых по варианту _j, .

Целевая функция

минимум отходов при раскрое

. (5.29)

Ограничение на удовлетворение спроса потребителя

. (5.30)

Пример 5.8. Многосторонний коммерческий арбитраж ( Таха X. Введение в исследование операций: В 2-х кн. – М.: Мир, 1985. ).

В сфере деятельности, связанной с валютными и биржевыми операциями, а также коммерческими сделками контрактного ха­рактера, возможны различного рода трансакции, позволяющие из­влекать прибыль на разнице в курсе валют. Такого рода трансак­ции называются коммерческим арбитражем.

Представим себе коммерсанта (условно назовем его N), имею­щего возможность реализовать многосторонний коммерческий ар­битраж. Предположим, что число валютных рынков, вовлеченных в трансакционную деятельность коммерсанта N, равняется шести, а максимальное число возможных трансакций равняется девяти. Подробные данные, характеризующие рассматриваемую задачу, приведены в табл. 5.2.

При трансакции x₁ продажа единицы валютного номинала (цен­ных бумаг) II позволяет приобрести r₁₁ единиц валютного номина­ла I. При трансакции x₇ взамен единицы валютного номинала I можно получить r₃₇ единиц валютного номинала III и r₆₇ единиц валютного номинала VI. Остальные трансакции расшифровывают­ся аналогично. Значения r_ij могут быть дробными. Заметим, что при любой трансакции x_i (i = 1, 2, 3, 4, 5) каждый из валютных но­миналов можно обменять на валютный номинал I. Следует обра­тить внимание на правило выбора знака перед показателями в табл. 5.2. Чтобы отличать куплю от продажи, будем соответственно ис­пользовать знаки «плюс» и «минус» перед показателями, характе­ризующими данную трансакцию.

Таблица 5.2. Многосторонний коммерческий арбитраж

Валютный номинал	Тип трансакции	Возмож-ность рынка
I	r11	r12	r13	r14	r15	-1	-1
II	-1					r26			r29
III		-1					r37	r38
IV			-1					-1
V				-1				r58
VI					-1		r67		-1
Размер транcакции	x1	x2	x3	x4	x5	x6	x7	x6	x9

 

Рассмотрим идеализированный случай, когда все трансакции коммерсанта N выполняются одновременно. Ограничения опреде­ляются единственным требованием – трансакция возможна лишь при условии, если коммерсант N располагает наличными ценными бумагами. Другими словами, количество проданных ценных бумаг не должно превышать количество приобретенных. Данные ограни­чения имеют вид

Пусть целевая функция представляет собой чистый доход, вы­раженный в единицах валютного номинала I, т. е. задача состоит в том, чтобы

Пример 5.9. Транспортная задача.

Имеется три поставщика и четыре потребителя однородной продукции. Известны затраты на перевозку груза от каждого поставщика каждому потребителю. Обозначим их . Запасы грузов у поставщиков равны 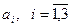. Известны потреб­ности каждого потребителя . Будем считать, что суммар­ные потребности равны суммарным запасам:

.

Требуется составить такой план перевозок, чтобы обеспечить минимальные суммарные затраты при полном удовлетворении по­требностей.

Введем переменные х_ij – количество груза, перевозимого от i -го поставщика j -му потребителю.

Ограничения задачи выглядят следующим образом:

• потребности всех потребителей должны быть удовлетворены пол­ностью:

(5.31)

или в общем виде:

;

• груз поставщика должен быть вывезен полностью:

(5.32)

или в общем виде:

;

• условие неотрицательности переменных:

.

Целевая функция – минимизировать суммарные затраты на пе­ревозку:

. (5.33)

Количество поставщиков и потребителей в общем случае может быть произвольным ().

Мы рассмотрели девять примеров типовых задач линейного про­граммирования. Обобщая их, можно сделать следующие выводы.

1. Ограничения в задачах линейного программирования могут
быть выражены как равенствами, так и неравенствами.

2. Линейная функция может стремиться как к максимуму, так
и к минимуму.

3.Переменные в задачах всегда неотрицательны.

Напомним, что от любой из вышеперечисленных задач можно

перейти к канонической (основной) задаче линейного программи­рования.

5.3. Графические методы решения задач линейного
программирования

Графический способ решения задач линейного программирова­ния целесообразно использовать для:

решения задач с двумя переменными, когда ограничения выра­жены неравенствами;

решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

Запишем задачу линейного программирования с двумя переменными:

Ø целевая функция:

(5.34)

Ø ограничения:

; (5.35)

. (5.36)

Каждое из неравенств (5.35) - (5.36) системы ограничений за­дачи геометрически определяет полуплоскость соответственно с граничными прямыми . В том случае, если система неравенств (5.35) - (5.36) совместна, об­ласть ее решений есть множество точек, принадлежащих всем ука­занным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых ре­шений является выпуклое множество, которое называется много­угольником решений. Стороны этого многоугольника лежат на пря­мых, уравнения которых получаются из исходной системы ограни­чений заменой знаков неравенств на знаки равенств.

Областью допустимых решений системы неравенств (5.35) — (5.36) может быть:

Ø выпуклый многоугольник;

Ø выпуклая многоугольная неограниченная область;

Ø пустая область;

Ø луч;

Ø отрезок;

Ø единственная точка.

Целевая функция (5.34) определяет на плоскости семейство па­раллельных прямых, каждой из которых соответствует определен­ное значение Z.

Вектор 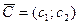с координатами с₁ и с₂, перпендикулярный к этим прямым, указывает направление наискорейшего возраста­ния Z, а противоположный вектор – направление убывания Z.

Если в одной и той же системе координат изобразить область допустимых решений системы неравенств (5.35) – (5.36) и семей­ство параллельных прямых (5.34), то задача определения максимума функции Z сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства Z = const, и которая соответствует наибольшему значению параметра Z.

Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины построим линию уровня , проходящую через начало координат и перпендикулярную вектору С = (с₁;с₂), и будем передвигать ее в направ­лении вектора 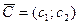до тех пор, пока она не коснется послед­ней крайней (угловой) точки многоугольника решений. Коорди­наты указанной точки и определяют оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации зада­чи (5.34) – (5.36), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 5.1 – 5.4. Рис. 5.1 харак­теризует такой случай, когда целевая функция принимает макси­мальное значение в единственной точке А. Из рис. 5.2 видно, что максимальное значение целевая функция принимает в любой точ­ке отрезка АВ.

На рис. 5.3. изображен случай, когда максимум недостижим, а на рис. 3.4 – случай, когда система ограничений задачи несовместима.

Рис. 5.1. Оптимум функции Z достижим в точке А

Рис. 5.2. Оптимум функции Z достижим в любой точке АВ

Рис. 5.3. Оптимум функции Z недостижим

Рис. 5.4. Область допустимых решений – пустая область

 

Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем. что линия уровня Z передвигается не в направлении вектора 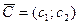, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Для практического решения задачи линейного программирования (5.34) – (5.36) на основе ее геометрической интерпретации необходи­мо следующее.

1. Построить прямые, уравнения которых получаются в резуль­тате замены в ограничениях (5.35) - (5.36) знаков неравенств на знаки равенств.

2. Найти полуплоскости, определяемые каждым из ограниче­ний задачи.

3. Определить многоугольник решений.

4. Построить вектор .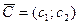

5. Построить прямую , проходящую через на­чало координат и перпендикулярную вектору С.

6. Передвигать прямую в направлении вектора С, в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.

Определить координаты точки максимума функции и вычис­лить значение целевой функции в этой точке.

Пример 5.10. Рассмотрим решение задачи об ассортименте про­дукции (Пример 5.2) геометрическим способом.

Решение

Построим многоугольник решений (рис. 5.5). Для этого в сис­теме координат Х₁0Х₂ на плоскости изобразим граничные прямые:

Взяв какую-либо точку, например начало координат, устано­вим, какую полуплоскость определяет соответствующее неравенст­во. Полуплоскости, определяемые неравенствами, на рис. 5.5 пока­заны стрелками. Областью решений является многоугольник OABCD.

Для построения прямой строим вектор-гради­ент и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора . Из рис. 5.5 следует, что по отноше­нию к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L₁ и L₃. Для определения ее коорди­нат решим систему уравнений:

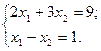
Оптимальный план задачи х₁ = 2,4; x₂ =1,4. Подставляя значе­ния х₁ и х₂ в линейную функцию, получим:

Рис. 5.5. Решение задачи линейного программирования
геометрическим способом

 

Полученное решение означает, что объем производства продук­ции П₁ должен быть равен 2,4 ед., а продукции П₂ – 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д. е.

Геометрическим способом можно также решать задачи линей­ного программирования с числом переменных более двух. Для это­го исходную задачу преобразуют методом Жордана—Гаусса.

Пример 5.11.

Используя метод Жордана-Гаусса, произведем два полных ис­ключения x₁ и x₄:

.

В результате приходим к системе

откуда

Подставляя эти значения в линейную функцию Z и отбрасывая в последней системе базисные переменные, получим задачу, выра­женную только через свободные неизвестные х₁ и x ₃. Найдем мак­симальное значение линейной функции

при следующих ограничениях:

Построим многоугольник решений и линейную функцию в си­стеме координат Х₂0Х₃ (рис. 5.6). Согласно рис. 3.6, линейная функ­ция принимает максимальное значение в точке А, которая лежит на пересечении прямых L₂ и Х₂= 0. Ее координаты (0;0,23).

Рис.5.6. Геометрическая интерпретация решения задачи
линейного программирования

Максимальное значение функции

Для отыскания оптимального плана исходной задачи подстав­ляем в преобразованную систему х₂ и x₃. Окончательно получаем X =(1,078; 0; 0,23; 0,001).

Симплекс-метод

Общая идея симплекс-метода

Для начала работы требуется, чтобы заданная система ограни­чений выражалась равенствами, причем в этой системе ограниче­ний должны быть выделены базисные неизвестные. Решение зада­чи при помощи симплекс-метода распадается на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому ба­зису с таким расчетом, чтобы значение функции Z уменьшалось, т. е. . Для перехода к новому базису из старого базиса уда­ляется одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый ба­зис для которого есть искомый минимум для линейной функции Z, а соответствующее базисное решение является опти­мальным либо выясняется, что задача не имеет решения.

Алгоритм симплекс-метода

Рассмотрим систему ограничений и линейную форму вида:

; (5.37)

(5.38)

. (5.39)

Используя метод Жордана – Гаусса, приведем записанную сис­тему к виду, где выделены базисные переменные. Введем условные обозначения:

– базисные переменные;

свободные переменные.

; (5.40)

(5.41)

По последней системе ограничений и целевой функции Z пост­роим табл. 5.3.

Таблица 5.3. Симплекс-таблица

Свободные неизвест- ные Базис- ные неизвестные	Свободный член	xr+1	xr+1	…	xr+1
x1	β1	a1r+1	a1r+2