На значимость модели
Мультиколлинеарность – попарная корреляционная зависимость между факторами.
Мультиколлинеарная зависимость присутствует, если коэффициент парной корреляции  .
.
Отрицательное воздействие мультиколлинеарности состоит в следующем:
1. Усложняется процедура выбора главных факторов.
2. Искажается смысл коэффициента множественной корреляции (он предполагает независимость факторов).
3. Усложняются вычисления при построении самой модели.
4. Снижается точность оценки параметров регрессии, искажается оценка дисперсии.
Следствием снижения точности является ненадежность коэффициентов регрессии и отчасти неприемлемость их использования для интерпретации как меры воздействия соответствующей объясняющей переменной на зависимую переменную.
Оценки коэффициента становятся очень чувствительными к выборочным наблюдениям. Небольшое увеличение объема выборки может привести к очень сильным сдвигам в значениях оценок. Кроме того, стандартные ошибки оценок входят в формулы критерия значимости, поэтому применение самих критериев становится также ненадежным. Из сказанного ясно, что исследователь должен пытаться установить стохастическую мультиколлинеарность и по возможности устранить ее.
Для измерения мультиколлинеарности можно использовать коэффициент множественной детерминации
 , (4.23)
, (4.23)
где R – коэффициент множественной корреляции.
При отсутствии мультиколлинеарности факторов
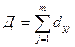 , (4.24)
, (4.24)
где dyj – коэффициент парной детерминации, вычисляемый по формуле
 , (4.25)
, (4.25)
где  – коэффициент парной корреляции между j -м фактором и зависимой переменной у.
– коэффициент парной корреляции между j -м фактором и зависимой переменной у.
При наличии мультиколлинеарности соотношение (4.24) не соблюдается. Поэтому в качестве меры мультиколлинеарности используется следующая разность:
 . (4.26)
. (4.26)
Чем меньше эта разность, тем меньше мультиколлинеарность. Для устранения мультиколлинеарности используется метод исключения переменных. Этот метод заключается в том, что высоко коррелированные объясняющие переменные (факторы) устраняются из регрессии и она заново оценивается. Отбор переменных, подлежащих исключению, производится с помощью коэффициентов парной корреляции. Опыт показывает, что если 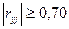 , то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия.
, то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия.
Обычно в модели оставляют тот фактор, на который можно разработать мероприятие, обеспечивающее улучшение значения этого фактора в планируемом году. Возможна ситуация, когда оба мультиколлинеарных фактора управляемы на уровне предприятия.
Решить вопрос об исключении того или иного фактора можно только в соответствии с процедурой отбора главных факторов.
Отбор факторов не самостоятельный процесс, он сопровождается построением модели. Принятие решения об исключении факторов производится на основе анализа значений специальных статистических характеристик и с учетом управляемости факторов на уровне предприятия.
Процедура отбора главных факторов обязательно включает следующие этапы:
1. Анализ факторов на мультиколлинеарностъ и ее исключение. Здесь производится анализ значений коэффициентов парной корреляции  между факторами хi и xj.
между факторами хi и xj.
2. Анализ тесноты взаимосвязи факторов (х) с зависимой переменной (у).
Для анализа тесноты взаимосвязи х и у используются значения коэффициента парной корреляции между фактором и функцией ( ). Величина
). Величина  определяется на ЭВМ и представлена в корреляционной матрице вида:
определяется на ЭВМ и представлена в корреляционной матрице вида:
| №
переменной
| x1
| x2
| x3
| …
| xm
| y
|
| x1
|
| 
| 
| …
| 
| 
|
| x2
| 
|
| 
| …
| 
| 
|
| x3
| 
| 
|
| …
| 
| 
|
| …
| …
| …
| …
| …
| …
| …
|
| xm
| 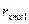
| 
| 
| …
|
| 
|
| y
| 
| 
| 
| …
| 
|
|
Факторы, для которых  = О, т. е. не связанные с у, подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение
= О, т. е. не связанные с у, подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение  , могут быть потенциально исключены из модели. Вопрос об их окончательном исключении решается в ходе анализа других статистических характеристик.
, могут быть потенциально исключены из модели. Вопрос об их окончательном исключении решается в ходе анализа других статистических характеристик.
3. Анализ коэффициентов р" факторов, которые потенциально могут быть исключены.
Коэффициент β учитывает влияние анализируемых факторов на у с учетом различий в уровне их колеблемости. Коэффициент β показывает, насколько сигм (средних квадратических отклонений) изменяется функция с изменением соответствующего аргумента на одну сигму при фиксированном значении остальных аргументов:
 , (4.27)
, (4.27)
Где  – коэффициент β k -roфактора;
– коэффициент β k -roфактора;  – среднее квадратическое отклонение k -гофактора;
– среднее квадратическое отклонение k -гофактора;  – среднее квадратическое отклонение функции;
– среднее квадратическое отклонение функции;  – коэффициент регрессии при к -мфакторе.
– коэффициент регрессии при к -мфакторе.
Из двух факторов хi и xj может быть исключен тот фактор, который имеет меньшее значение β.
Допустим, исключению подлежит один из мультиколлинеарных факторов хi или xj. Оба фактора управляемы на уровне предприятия, коэффициенты регрессии а i и а j статистически значимы. Фактор хi более тесно связан с у, т. е.  , но при этом
, но при этом  . В этом случае обычно исключению подлежит фактор xj.
. В этом случае обычно исключению подлежит фактор xj.
4. Проверка коэффициентов регрессии на статистическую значимость.
Проверка может быть произведена двумя способами:
• проверка статистической значимости ак по критерию Стьюдента проводится по следующей формуле:
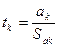 , (4.27)
, (4.27)
где а k – коэффициент регрессии при к-м факторе;
Sak – стандартное отклонение оценки параметра ак (Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа. - М.: Финансы и статистика, 1983).
Число степеней свободы статистики tk равно f = п - т -1, где т – количество факторов, включенных в модель. Значение /, вычисляемое по (4.28), сравнивают с критическим значением tfa, найденным по таблице Приложения 1 при заданном уровне значимости а и числе степеней свободы f (двухсторонняя критическая область).
Если tk > tfa, то ак существенно больше 0, а фактор хк оказывает существенное влияние на у. При этом фактор хк оставляем в модели. Если tk < tfa, то фактор исключаем из модели;
• проверка статистической значимости ак по критерию Фишера –
 , (4.29)
, (4.29)
где t2 - многомерный аналог критерия Стьюдента.
Число степеней свободы статистики Fk следующее: f1 = 1, f 2 = п – т-1. Значение Fk, вычисляемое по формуле (4.29), сравнивают с критическим значением  , найденным по таблице Приложения 2, при заданных уровне значимости а и числе степеней свободы f1, f 2.
, найденным по таблице Приложения 2, при заданных уровне значимости а и числе степеней свободы f1, f 2.
Если  , то ак — существенно больше 0, а фактор хк оказывает существенное влияние на у. При этом фактор хк оставляем в модели. Если
, то ак — существенно больше 0, а фактор хк оказывает существенное влияние на у. При этом фактор хк оставляем в модели. Если  , то фактор исключаем из модели.
, то фактор исключаем из модели.
5. Анализ факторов на управляемость.
В ходе логического анализа на основе экономических знаний исследователь должен сделать вывод: можно ли разработать организационно-технические мероприятия, направленные на улучшение (изменение) выбранных факторов на уровне предприятия. Если это возможно, то данные факторы управляемы. Неуправляемые факторы на уровне предприятия могут быть исключены из модели. Например, из двух факторов х1 – средняя техническая скорость автомобилей и х2 – время погрузки-разгрузки на одну ездку при равенстве или близких по значению таких характеристик, как  и
и  , βx1 и βx2 исключению подлежит x1. На уровне АТП практически невозможно повлиять на значение технической скорости, которая зависит в основном от климатических условий и величины транспортного потока.
, βx1 и βx2 исключению подлежит x1. На уровне АТП практически невозможно повлиять на значение технической скорости, которая зависит в основном от климатических условий и величины транспортного потока.
6. Строится новая регрессионная модель без исключенных факторов. Для этой модели определяется коэффициент множественной
детерминации Д.
7. Исследование целесообразности исключения факторов из модели с помощью коэффициента детерминации.
Прежде чем вынести решение об исключении переменных из анализа в силу их незначимого влияния на зависимую переменную, производят исследования с помощью коэффициента детерминации.
В первой регрессии содержится т объясняющих переменных, во второй – только часть из них, а именно т1 объясняющих переменных. При этом т = m1 + т2, т.е. во вторую регрессию мы не включили т2 объясняющих переменных. Теперь следует проверить, вносят ли совместно эти т2 переменных существенную долю в объяснение вариации переменной у. Для этого используется статистика
 , (4.30)
, (4.30)
которая имеет F -распределение c  и
и  степенями свободы. Здесь Дт означает коэффициент детерминации регрессии с т объясняющими переменными, а Дт1 – коэффициент детерминации регрессии с m1 факторами.
степенями свободы. Здесь Дт означает коэффициент детерминации регрессии с т объясняющими переменными, а Дт1 – коэффициент детерминации регрессии с m1 факторами.
Разность (Дт - Дт1) в числителе формулы является мерой дополнительного объяснения вариации переменной у за счет включения т2 переменных.
Критическое значение  находят по таблице F -распределения при заданном уровне значимости а и f 1 и f 2 степенях свободы. Если
находят по таблице F -распределения при заданном уровне значимости а и f 1 и f 2 степенях свободы. Если  , то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную у. Если
, то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную у. Если  , то т2, объясняющих переменных совместно оказывают существенное влияние на вариацию переменной у, и, следовательно, в этом случае все т2 переменные нельзя исключать из модели.
, то т2, объясняющих переменных совместно оказывают существенное влияние на вариацию переменной у, и, следовательно, в этом случае все т2 переменные нельзя исключать из модели.
При реализации первой ситуации ( )факторы окончательно исключаются из модели.
)факторы окончательно исключаются из модели.
7. Проверка адекватности модели. Данный этап анализа включает:
• оценку значимости коэффициента детерминации. Данная оценка необходима для решения вопроса: оказывают ли выбранные факторы влияние на зависимую переменную? Оценку значимости Д следует проводить, так как может сложиться такая ситуация, когда величина коэффициента детерминации будет целиком обусловлена случайными колебаниями в выборке, на основании которой он вычислен. Это объясняется тем, что величина Д существенно зависит от объема выборки.
Для оценки значимости коэффициента множественной детерминации используется следующая статистика:
 , (4.31)
, (4.31)
которая имеет F -распределение с  и
и  степенями свободы. Здесь Д = R2, а т – количество учитываемых объясняющих переменных (факторов).
степенями свободы. Здесь Д = R2, а т – количество учитываемых объясняющих переменных (факторов).
Значение статистики F, вычисленное по эмпирическим данным, сравнивается с табличным значением  . Критическое значение определяется по таблице Приложения 2 по заданному а и степеням свободы f1 и f 2. Если
. Критическое значение определяется по таблице Приложения 2 по заданному а и степеням свободы f1 и f 2. Если  , то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);
, то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);
• проверку качества подбора теоретического уравнения. Она проводится с использованием средней ошибки аппроксимации. Средняя ошибка аппроксимации регрессии определяется по формуле:
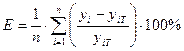 ; (4.32)
; (4.32)
вычисление специальных показателей, которые применяются для характеристики воздействия отдельных факторов на результирующий показатель. Это коэффициент эластичности, который показывает, насколько процентов в среднем изменяется функция с изменением аргумента на 1% при фиксированных значениях других аргументов:
 ; (4.33)
; (4.33)
доля влияния каждого фактора xj в отдельности на вариацию у (Елисеева И. И., Юзбашев М. М. Общая теория статистики. — М.: Финансы и статистика, 1999):
 , (4.34)
, (4.34)
где  – коэффициент бетта фактора xj.
– коэффициент бетта фактора xj.
Показатель gj является мерой вариации результативного признака за счет изолированного влияния фактора xj. Следует отметить, что система факторов, входящая в модель регрессии, — это не простая их сумма, так как система предполагает внутренние связи, взаимодействие составляющих ее элементов. Действие системы не равно арифметической сумме воздействий составляющих ее элементов. Поэтому необходимо определить показатель системного эффекта факторов  :
:
 .
.
На основе анализа специальных показателей и значений парной корреляции х с у делают вывод, какие из главных факторов оказывают наибольшее влияние на у. После этого переходят к разработке организационно-технических мероприятий, направленных на улучшение значений этих факторов, с целью повышения (снижения) результативного показателя у.
8. Экономическая интерпретация.
Результаты регрессионного анализа сравниваются с гипотезами, сформулированными на первом этапе исследования, и оценивается их правдоподобие с экономической точки зрения.
9. Прогнозирование неизвестных значений зависимой переменой.
Полученное уравнение регрессии находит практическое применение в прогностическом анализе. Прогноз получают путем подстановки в регрессию с численно оцененными параметрами значений факторов. Следует подчеркнуть, что прогнозирование результатов по регрессии лучше поддается содержательной интерпретации, чем простая экстраполяция тенденций, так как полнее учитывается природа исследуемого явления. Более подробно вопросы прогнозирования рассмотрены в работе: Бережная Е.В., Бережной В.И. Математические методы и моделирование экономических систем: учебное пособие. – М.: Финансы и статистика, 2003. – 368 с..
Часть 5
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ В РЕШЕНИИ ОПТИМИЗАЦИОННЫХ ЗАДАЧ
Оптимизационная задача — это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
В самом общем виде задача математически записывается так:
 . (5.1)
. (5.1)
где  ;
;
W – область допустимых значений переменных х1, х2,..., хn;
f(Х) – целевая функция.
Для того чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т. е. указать  такое, что
такое, что  при любом
при любом  , или для случая минимизации –
, или для случая минимизации –  при любом
при любом  .
.
Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешима, если целевая функция f(X) не ограничена сверху на допустимом множестве W.
Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией п переменных, то методы решения называют методами математического программирования.
В математическом программировании принято выделять следующие основные задачи в зависимости от вида целевой функции f(X) и от области W:
Ø задачи линейного программирования, если f(X) и W линейны;
Ø 






 задачи целочисленного программирования, если ставится условие целочисленности переменных xt, х2,..., хп;
задачи целочисленного программирования, если ставится условие целочисленности переменных xt, х2,..., хп;
Ø задачи нелинейного программирования, если форма f(X) носит
нелинейный характер.



 .
. , (4.23)
, (4.23)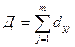 , (4.24)
, (4.24) , (4.25)
, (4.25) – коэффициент парной корреляции между j -м фактором и зависимой переменной у.
– коэффициент парной корреляции между j -м фактором и зависимой переменной у. . (4.26)
. (4.26)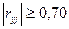 , то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия.
, то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия. между факторами хi и xj.
между факторами хi и xj.











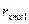







 , (4.27)
, (4.27) – коэффициент β k -roфактора;
– коэффициент β k -roфактора;  – среднее квадратическое отклонение k -гофактора;
– среднее квадратическое отклонение k -гофактора;  – среднее квадратическое отклонение функции;
– среднее квадратическое отклонение функции;  – коэффициент регрессии при к -мфакторе.
– коэффициент регрессии при к -мфакторе. , но при этом
, но при этом  . В этом случае обычно исключению подлежит фактор xj.
. В этом случае обычно исключению подлежит фактор xj.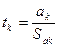 , (4.27)
, (4.27) , (4.29)
, (4.29) , найденным по таблице Приложения 2, при заданных уровне значимости а и числе степеней свободы f1, f 2.
, найденным по таблице Приложения 2, при заданных уровне значимости а и числе степеней свободы f1, f 2. , то ак — существенно больше 0, а фактор хк оказывает существенное влияние на у. При этом фактор хк оставляем в модели. Если
, то ак — существенно больше 0, а фактор хк оказывает существенное влияние на у. При этом фактор хк оставляем в модели. Если  , то фактор исключаем из модели.
, то фактор исключаем из модели. и
и  , βx1 и βx2 исключению подлежит x1. На уровне АТП практически невозможно повлиять на значение технической скорости, которая зависит в основном от климатических условий и величины транспортного потока.
, βx1 и βx2 исключению подлежит x1. На уровне АТП практически невозможно повлиять на значение технической скорости, которая зависит в основном от климатических условий и величины транспортного потока. , (4.30)
, (4.30) и
и  степенями свободы. Здесь Дт означает коэффициент детерминации регрессии с т объясняющими переменными, а Дт1 – коэффициент детерминации регрессии с m1 факторами.
степенями свободы. Здесь Дт означает коэффициент детерминации регрессии с т объясняющими переменными, а Дт1 – коэффициент детерминации регрессии с m1 факторами. находят по таблице F -распределения при заданном уровне значимости а и f 1 и f 2 степенях свободы. Если
находят по таблице F -распределения при заданном уровне значимости а и f 1 и f 2 степенях свободы. Если  , то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную у. Если
, то включение дополнительно объясняющих переменных совместно не оказывает значимого влияния на переменную у. Если  , то т2, объясняющих переменных совместно оказывают существенное влияние на вариацию переменной у, и, следовательно, в этом случае все т2 переменные нельзя исключать из модели.
, то т2, объясняющих переменных совместно оказывают существенное влияние на вариацию переменной у, и, следовательно, в этом случае все т2 переменные нельзя исключать из модели. , (4.31)
, (4.31) и
и  , то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);
, то вычисленный коэффициент детерминации значимо отличается от 0 и, следовательно, включенные в регрессию переменные достаточно объясняют зависимую переменную, что позволяет говорить о значимости самой регрессии (модели);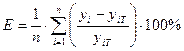 ; (4.32)
; (4.32) ; (4.33)
; (4.33) , (4.34)
, (4.34) – коэффициент бетта фактора xj.
– коэффициент бетта фактора xj. :
: .
. . (5.1)
. (5.1) ;
; такое, что
такое, что  при любом
при любом  , или для случая минимизации –
, или для случая минимизации –  при любом
при любом 






 задачи целочисленного программирования, если ставится условие целочисленности переменных xt, х2,..., хп;
задачи целочисленного программирования, если ставится условие целочисленности переменных xt, х2,..., хп;


