Моделирование случайного события заключается в воспроизведении факта появления или непоявления случайного события в соответствии с заданной его вероятностью. Моделирование полной группы несовместных событий Аь А2,..., А„, вероятности которых  , и известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения
, и известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения
 ,
,
где вероятности ее возможных значений
 .
.
Очевидно, что принятие в испытании дискретной случайной величиной Y возможного значения  равносильно появлению в испытании события Аi. При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы
равносильно появлению в испытании события Аi. При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы  (рис. 3.1).
(рис. 3.1).

Рис. 3.1. Интервалы 
Вырабатывают равномерно распределенное на интервале [0,1] случайное число  и проверяют условие
и проверяют условие
 . (3.10)
. (3.10)
При выполнении условия (3.10) считают, что при испытании наступило событие Аk.
Нетрудно заметить, что моделирование факта появления одного события А, имеющего вероятность Р(А), сводится к моделированию полной группы двух несовместных событий, т. е. противоположных событий с вероятностями  и
и  .
.
Пример 3.4. Вероятность появления события А в каждом испытании Р(А) = 0,75.
Смоделируйте три испытания и определите последовательность реализации события А.
Решение
Отложим на единичном отрезке числовой оси точку Е = 0,75 и будем считать, что если случайное число  , то в испытании наступило событие А. В противном случае при
, то в испытании наступило событие А. В противном случае при  наступило событие
наступило событие  , т. е. событие А не имело места.
, т. е. событие А не имело места.
Пусть из таблицы выбраны равномерно распределенные на интервале [0,11 случайные числа  = 0,925;
= 0,925;  ~ 0,135;
~ 0,135;  = 0,088. Тогда при трех испытаниях_получим следующую последовательность реализации событий:
= 0,088. Тогда при трех испытаниях_получим следующую последовательность реализации событий:  ; А; А.
; А; А.
Моделирование совместных (зависимых и независимых) событий можно выполнить двумя способами.
Первый способ. На первом этапе моделирования определяют все возможные исходы появления совместных событий в испытании (находят полную группу несовместных событий и вычисляют их вероятности). На последующем этапе работ поступают так же, как и при моделировании полной группы несовместных событий.
Пример 3.5. Пусть при испытании могут иметь место зависимые и совместные события А и В, при этом известно, что Р{А) = 0,7; Р(В) = 0,5; Р(АВ) = 0,3.
Смоделируйте появление событий А и В в двух испытаниях.
Решение
При каждом испытании возможны четыре несовместных исхода, т.е. наступление четырех событий:
1. С1 = АВ, при этом по условию Р(С1) = Р(АВ) = 0,3.
2. С2 =  ,
,
при этом Р(С2) = Р(АВ) = Р(А) -Р(ВА) = 0,7 - 0,3 = 0,4.
3. С3 = АВ,
при этом Р{С3) = Р( ) = Р(В) - Р(АВ) = 0,5 - 0,3 = 0,2.
) = Р(В) - Р(АВ) = 0,5 - 0,3 = 0,2.
4. С4 =  ,
,
при этом Р(С4) =  = 1 - (0,3 + 0,4 + 0,2) = 0,1.
= 1 - (0,3 + 0,4 + 0,2) = 0,1.
Смоделируем полную группу событий C1, С2, С3, С4 в двух испытаниях. Предварительно на единичном отрезке числовой оси (рис. 3.2) откладываем интервалы  .
.

Рис. 3.2. Интервалы 
Пусть получены (взяты из таблицы) случайные числа  = 0,68 и
= 0,68 и  = 0,95. Случайное число
= 0,95. Случайное число  принадлежит интервалу Δ2, поэтому при первом испытании имело место событие А, а событие В не наступило. При втором испытании случайное число
принадлежит интервалу Δ2, поэтому при первом испытании имело место событие А, а событие В не наступило. При втором испытании случайное число  принадлежит интервалу Δ4. Оба события А и В не имели места.
принадлежит интервалу Δ4. Оба события А и В не имели места.
Второй способ. Моделирование совместных событий состоит в разыгрывании факта появления каждого из совместных событий отдельно, при этом, если события зависимые, необходимо предварительно определить условные вероятности.
Пример 3.6. Используя условия примера 3.5, смоделируйте раздельное появление событий А и В в одном испытании.
Решение
События А и В зависимы, поэтому предварительно находим условные вероятности Р(В/А) и Р(В/  ):
):
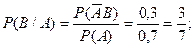

Для моделирования события А выработаем случайное число  Пусть
Пусть  = 0,96, так как
= 0,96, так как  > Р(А). Событие А в испытании не наступило.
> Р(А). Событие А в испытании не наступило.
Теперь разыграем событие В при условии, что событие А в испытании не имело место. Пусть случайное число  = 0,22, тогда,
= 0,22, тогда,  т. е.
т. е.  . Событие В при испытании наступило.
. Событие В при испытании наступило.



 , и известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения
, и известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения ,
, .
. равносильно появлению в испытании события Аi. При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы
равносильно появлению в испытании события Аi. При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы  (рис. 3.1).
(рис. 3.1).
 и проверяют условие
и проверяют условие . (3.10)
. (3.10) и
и  .
. , то в испытании наступило событие А. В противном случае при
, то в испытании наступило событие А. В противном случае при  наступило событие
наступило событие  , т. е. событие А не имело места.
, т. е. событие А не имело места. = 0,925;
= 0,925;  ~ 0,135;
~ 0,135;  = 0,088. Тогда при трех испытаниях_получим следующую последовательность реализации событий:
= 0,088. Тогда при трех испытаниях_получим следующую последовательность реализации событий:  ,
, = 1 - (0,3 + 0,4 + 0,2) = 0,1.
= 1 - (0,3 + 0,4 + 0,2) = 0,1. .
.

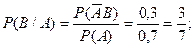

 = 0,22, тогда,
= 0,22, тогда,  т. е.
т. е.  . Событие В при испытании наступило.
. Событие В при испытании наступило.


