На этом этапе проводятся серийные расчеты по составленной и отлаженной программе. Этап включает следующие подэтапы:
v планирование машинного эксперимента;
v проведение рабочих расчетов;
v представление результатов моделирования;
v интерпретация результатов моделирования;
v выдача рекомендаций по оптимизации режима работы реальной системы.
Перед проведением рабочих расчетов на ЭВМ должен быть составлен план проведения эксперимента с указанием комбинации переменных и параметров, для которых должно проводиться моделирование системы. Задача заключается в разработке оптимального плана эксперимента, реализация которого позволяет при сравнительно небольшом числе испытаний модели получить достоверные данные о закономерностях функционирования системы.
Результаты моделирования могут быть представлены в виде таблиц, графиков. диаграмм, схем и т.п. В большинстве случаев наиболее простой формой считаются таблицы, хотя графики более наглядно иллюстрируют результаты моделирования системы. Целесообразно предусмотреть вывод результатов на экран дисплея и принтер.
Интерпретация результатов моделирования имеет целью переход от информации, полученной в результате машинного эксперимента с моделью, к выводам, касающимся процесса функционирования объекта-оригинала.
На основании анализа результатов моделирования принимается решение о том, при каких условиях система будет функционировать с наибольшей эффективностью.
Часть 2
ПРИМЕРЫ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Пример 1.
Пусть некоторый экономический регион производит несколько (n) видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения на эти товары изучен. Надо определить годовой объем выпуска продуктов, с учетом того, что этот объем должен обеспечить как конечное, так и производственное потребление.
Составим математическую модель этой задачи. По ее условию даны: виды продуктов, спрос на них и технологический процесс; требуется найти объем выпуска каждого вида продукта.
Обозначим известные величины:
c i – спрос населения на i -й продукт (i =1,..., n); a ij – количество i -го продукта, необходимое для выпуска единицы j -го продукта по данной технологии (i =1,..., n; j =1,..., n);
Обозначим неизвестные величины:
х i – объем выпуска i -го продукта (i =1,..., n); совокупность с =(c 1,..., c n) называется вектором спроса, числа a ij – технологическими коэффициентами, а совокупность х =(х 1,..., х n) – вектором выпуска.
По условию задачи вектор х распределяется на две части: на конечное потребление (вектор с) и на воспроизводство (вектор х-с). Вычислим ту часть вектора х которая идет на воспроизводство. По нашим обозначениям для производства х j количества j-го товара идет a ij · х j количества i -го товара.
Тогда сумма a i1 · х 1 +...+ a in · х n показывает ту величину i -го товара, которая нужна для всего выпуска х =(х 1,..., х n).
Следовательно, должно выполняться равенство:
 .
.
Распространяя это рассуждение на все виды продуктов, приходим к искомой модели:

Решая эту систему из n линейных уравнений относительно х1,...,хn и найдем требуемый вектор выпуска.
Для того, чтобы написать эту модель в более компактной (векторной) форме, введем обозначения:

Квадратная ( ) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х - с = Ах или
) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х - с = Ах или
 (1.6)
(1.6)
Мы получили классическую модель «Затраты – выпуск», автором которой является известный американский экономист В. Леонтьев.
Пример 2.
Нефтеперерабатывающий завод располагает двумя сортами нефти: сортом А в количестве 10 единиц, сортом В — 15 единиц. При переработке из нефти получаются два материала: бензин (обозначим Б) и мазут (М). Имеется три варианта технологического процесса переработки:
I: 1ед. А + 2ед. В дает 3ед. Б + 2ед. М
II: 2ед. А + 1ед. В дает 1ед. Б + 5ед. М
III: 2ед. А + 2ед. В дает 1ед. Б + 2ед. М
Цена бензина — 10 долл. за единицу, мазута — 1 долл. за единицу.
Требуется определить наиболее выгодное сочетание технологических процессов переработки имеющегося количества нефти.
Перед моделированием уточним следующие моменты. Из условия задачи следует, что «выгодность» технологического процесса для завода следует понимать в смысле получения максимального дохода от реализации своей готовой продукции (бензина и мазута). В связи с этим понятно, что «выбор (принятие) решения» завода состоит в определении того, какую технологию и сколько раз применить. Очевидно, что таких возможных вариантов достаточно много.
Обозначим неизвестные величины:
х i – количество использования i -го технологического процесса (i=1,2,3).
Остальные параметры модели (запасы сортов нефти, цены бензина и мазута) известны.
Теперь одно конкретное решение завода сводится к выбору одного вектора х =(х1,х2,х3), для которого выручка завода равна (32х1+15х2 +12х3) долл. Здесь 32 долл. – это доход, полученный от одного применения первого технологического процесса (10 долл. ·3ед. Б + 1 долл. ·2ед. М = 32 долл.). Аналогичный смысл имеют коэффициенты 15 и 12 для второго и третьего технологических процессов соответственно. Учет запаса нефти приводит к следующим условиям:
для сорта А: 
для сорта В:  ,
,
где в первом неравенстве коэффициенты 1, 2, 2 – это нормы расхода нефти сорта А для одноразового применения технологических процессов I, II, III соответственно. Коэффициенты второго неравенства имеют аналогичный смысл для нефти сорта В.
Математическая модель в целом имеет вид:
Найти такой вектор х = (х1,х2,х3), чтобы максимизировать
f(x) =32х1+15х2 +12х3
при выполнении условий:


 .
.
Сокращенная форма этой записи такова:
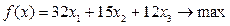
при ограничениях
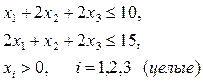 (2.1)
(2.1)
Мы получили так называемую задачу линейного программирования.
Модель (2.1.) является примером оптимизационной модели детерминированного типа (с вполне определенными элементами).
Пример 3.
Инвестору требуется определить наилучший набор из акций, облигаций и других ценных бумаг для приобретения их на некоторую сумму с целью получения определенной прибыли с минимальным риском для себя. Прибыль на каждый доллар, вложенный в ценную бумагу j - го вида, характеризуется двумя показателями: ожидаемой прибылью и фактической прибылью. Для инвестора желательно, чтобы ожидаемая прибыль на один доллар вложений была для всего набора ценных бумаг не ниже заданной величины b.
Заметим, что для правильного моделирования этой задачи от математика требуются определенные базовые знания в области портфельной теории ценных бумаг.
Обозначим известные параметры задачи:
n – число разновидностей ценных бумаг; аj – фактическая прибыль (случайное число) от j-го вида ценной бумаги;  – ожидаемая прибыль от j -го вида ценной бумаги.
– ожидаемая прибыль от j -го вида ценной бумаги.
Обозначим неизвестные величины:
yj — средства, выделенные для приобретения ценных бумаг вида j.
По нашим обозначениям вся инвестированная сумма выражается как  .
.
Для упрощения модели введем новые величины
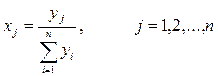 .
.
Таким образом, хi — это доля от всех средств, выделяемая для приобретения ценных бумаг вида j.
Ясно, что 
Из условия задачи видно, что цель инвестора — достижение определенного уровня прибыли с минимальным риском. Содержательно риск — это мера отклонения фактической прибыли от ожидаемой. Поэтому его можно отождествить с ковариацией  прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.
прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.
Математическая модель исходной задачи имеет вид:

при ограничениях
 ,
, 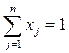 ,
,  ,
,  . (2.2)
. (2.2)
Мы получили известную модель Марковица для оптимизации структуры портфеля ценных бумаг.
Модель (2.2.) является примеров оптимизационной модели стохастического типа (с элементами случайности).
Пример 4.
На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль рj, если же он не будет пользоваться спросом - убыток qj.
Перед моделированием обсудим некоторые принципиальные моменты. В данной задаче лицом, принимающим решение (ЛПР), является магазин. Однако исход (получение максимальной прибыли) зависит не только от его решения, но и от того, будет ли завезенный товар пользоваться спросом, т. е. будет ли выкуплен населением (предполагается, что по какой-то причине у магазина нет возможности изучить спрос населения). Поэтому население может рассматриваться как второе ЛПР, выбирающее тип товара согласно своего предпочтения. Наихудшим для магазина «решением» населения является: «завезенный товар не пользуется спросом». Так что, для учета всевозможных ситуаций, магазину нужно считать население своим «противником» (условно), преследующим противоположную цель – минимизировать прибыль магазина.
Итак, имеем задачу принятия решения с двумя участниками, преследующими противоположные цели. Уточним, что магазин выбирает один из типов товаров для продажи (всего n вариантов решений), а население — один из типов товаров, который пользуется наибольшим спросом (n вариантов решений).
Для составления математической модели нарисуем таблицу с n строками и n столбцами (всего n2 клеток) и условимся, что строки соответствуют выбору магазина, а столбики — выбору населения. Тогда клетка (i, j) соответствует той ситуации, когда магазин выбирает i -й тип товара (i -ю строку), а население выбирает j -й тип товара (j- ю столбик). В каждую клетку запишем числовую оценку (прибыль или убыток) соответствующей ситуации с точки зрения магазина:

Числа qi написаны с минусом для отражения убытка магазина; в каждой ситуации «выигрыш» населения (условно) равен «выигрышу» магазина, взятому с обратным знаком.
Сокращенный вид этой модели таков:
 (2.3)
(2.3)
Мы получили так называемую матричную игру. Модель (2.3.) является примером игровых моделей принятия решения.
Часть 3
СТАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ
Теоретические основы метода
Метод статистического моделирования (или метод Монте-Карло) – это способ исследования поведения вероятностных систем (экономических, технических и т. д.) в условиях, когда не известны в полной мере внутренние взаимодействия в этих системах.
Этот метод заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Одно такое воспроизведение функционирования системы называют реализацией или испытанием. После каждого испытания регистрируют совокупность параметров, характеризующих случайный исход реализации. Метод основан на многократных испытаниях построенной модели с последующей статистической обработкой полученных данных с целью определения числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров. Процесс моделирования функционирования экономической системы сводится к машинной имитации изучаемого процесса, который как бы копируется на ЭВМ со всеми сопровождающими его случайностями.
Первые сведения о методе Монте-Карло были опубликованы в конце 40-х гг. Авторами метода являются американские математики Дж. Нейман и С. Улам. В нашей стране первые работы были опубликованы в 1955-1956 гг. В.В. Чавчанидзе, Ю.А. Шрейдером и B.C. Владимировым.
Основой метода статистического моделирования является закон больших чисел. Закон больших чисел в теории вероятностей доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к некоторым постоянным величинам.
Под законом больших чисел понимают ряд теорем. Например, одна из теорем П.Л. Чебышева формулируется так: «При неограниченном увеличении числа независимых испытаний п среднее арифметическое свободных от систематических ошибок и равноточных результатов наблюдений  случайной величины
случайной величины  , имеющей конечную дисперсию
, имеющей конечную дисперсию  , сходится по вероятности к математическому ожиданию
, сходится по вероятности к математическому ожиданию 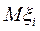 этой случайной величины». Это можно записать в следующем виде:
этой случайной величины». Это можно записать в следующем виде:
 , (3.1)
, (3.1)
где  – сколь угодно малая положительная величина.
– сколь угодно малая положительная величина.
Теорема Бернулли формулируется так: «При неограниченном увеличении числа независимых испытаний в одних и тех же условиях частота  наступления случайного события А сходится по вероятности к его вероятности Р», т. е.
наступления случайного события А сходится по вероятности к его вероятности Р», т. е.
 . (3.2)
. (3.2)
Согласно данной теореме, для получения вероятности какого-либо события, например вероятности состояний некоторой систе-
*
мы  , вычисляют частоты
, вычисляют частоты  для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного п. Результаты усредняют и этим самым с некоторым приближением, получают искомые вероятности состояний системы. На основании вычисленных вероятностей определяют другие характеристики системы. Следует отметить, что чем больше число реализаций я, тем точнее результаты вычисления искомых величин (вероятностей состояний системы).
для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного п. Результаты усредняют и этим самым с некоторым приближением, получают искомые вероятности состояний системы. На основании вычисленных вероятностей определяют другие характеристики системы. Следует отметить, что чем больше число реализаций я, тем точнее результаты вычисления искомых величин (вероятностей состояний системы).
Последнее утверждение легко доказать. Предположим, что требуется найти неизвестную величину т. Подберем такую случайную
величину  , чтобы
, чтобы 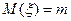 и
и  . Рассмотрим n случайных
. Рассмотрим n случайных
величин  , распределение которых совпадает с распределением
, распределение которых совпадает с распределением  . Если п достаточно велико, то согласно центральной
. Если п достаточно велико, то согласно центральной
предельной теореме распределение суммы  будет приближенно нормальным с параметрами
будет приближенно нормальным с параметрами  .
.
Из правила «трех сигм»
 (3.3)
(3.3)
Следует, что
 .
.
Разделим неравенство, стоящее в фигурной скобке, на n и получим эквивалентное неравенство с той же вероятностью:
 .
.
Это соотношение можно записать в виде
 . (3.4) Соотношение (3.4) определяет метод расчета т и оценку погрешности. В самом деле, найдем п значений случайной величины
. (3.4) Соотношение (3.4) определяет метод расчета т и оценку погрешности. В самом деле, найдем п значений случайной величины  . Из выражения (3.4) видно, что среднее арифметическое этих значений будет приближенно равно т. С вероятностью Р = 0,997 ошибка такого приближения не превосходит величины
. Из выражения (3.4) видно, что среднее арифметическое этих значений будет приближенно равно т. С вероятностью Р = 0,997 ошибка такого приближения не превосходит величины  . Очевидно, эта ошибка стремится к нулю с ростом п, что и требовалось доказать.
. Очевидно, эта ошибка стремится к нулю с ростом п, что и требовалось доказать.
Решение любой задачи методом статистического моделирования состоит в:
Ø разработке и построении структурной схемы процесса, выявлении основных взаимосвязей;
Ø формальном описании процесса;
Ø моделировании случайных явлений (случайных событий, случайных величин, случайных функций), сопровождающих функционирование исследуемой системы;
Ø моделировании (с использованием данных, полученных на предыдущем этапе) функционирования системы – воспроизведении процесса в соответствии с разработанной структурной схемой и формальным описанием;
Ø накоплении результатов моделирования, их статистической обработке, анализе и обобщении.
В отличие от описанных ранее математических моделей, результаты которых отражали устойчивое во времени поведение системы, результаты, получаемые при статистическом моделировании, подвержены экспериментальным ошибкам. Это означает, что любое утверждение, касающееся характеристик моделируемой системы, должно основываются на результатах соответствующих статистических проверок.
Экспериментальные ошибки при статистическом моделировании в значительной степени зависят от точности моделирования случайных явлений, сопровождающих функционирование исследуемой системы.
Известно, что при изучении вероятностных систем случайные явления могут интерпретироваться в виде случайных событий, случайных величин и случайных функций. Следовательно, моделирование случайных явлений сводится к моделированию случайных событий, случайных величин и случайных функций. Так как случайные события и случайные функции могут быть представлены через случайные величины, то и моделирование случайных событий и случайных функций производится с помощью случайных величин. В связи с этим рассмотрим сначала способы моделирования случайных величин.



 .
.

 ) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х - с = Ах или
) —матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х - с = Ах или (1.6)
(1.6)
 ,
, .
.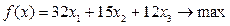
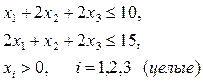 (2.1)
(2.1) – ожидаемая прибыль от j -го вида ценной бумаги.
– ожидаемая прибыль от j -го вида ценной бумаги. .
. 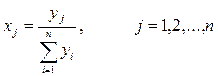 .
.
 прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.
прибыли для ценных бумаг вида i и вида j. Здесь М — обозначение математического ожидания.
 ,
, 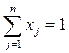 ,
,  ,
,  . (2.2)
. (2.2)
 (2.3)
(2.3) случайной величины
случайной величины  , сходится по вероятности к математическому ожиданию
, сходится по вероятности к математическому ожиданию 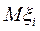 этой случайной величины». Это можно записать в следующем виде:
этой случайной величины». Это можно записать в следующем виде: , (3.1)
, (3.1) – сколь угодно малая положительная величина.
– сколь угодно малая положительная величина. наступления случайного события А сходится по вероятности к его вероятности Р», т. е.
наступления случайного события А сходится по вероятности к его вероятности Р», т. е. . (3.2)
. (3.2) , вычисляют частоты
, вычисляют частоты  для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного п. Результаты усредняют и этим самым с некоторым приближением, получают искомые вероятности состояний системы. На основании вычисленных вероятностей определяют другие характеристики системы. Следует отметить, что чем больше число реализаций я, тем точнее результаты вычисления искомых величин (вероятностей состояний системы).
для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного п. Результаты усредняют и этим самым с некоторым приближением, получают искомые вероятности состояний системы. На основании вычисленных вероятностей определяют другие характеристики системы. Следует отметить, что чем больше число реализаций я, тем точнее результаты вычисления искомых величин (вероятностей состояний системы). , чтобы
, чтобы 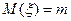 и
и  . Рассмотрим n случайных
. Рассмотрим n случайных , распределение которых совпадает с распределением
, распределение которых совпадает с распределением  будет приближенно нормальным с параметрами
будет приближенно нормальным с параметрами  .
. (3.3)
(3.3) .
. .
. . (3.4) Соотношение (3.4) определяет метод расчета т и оценку погрешности. В самом деле, найдем п значений случайной величины
. (3.4) Соотношение (3.4) определяет метод расчета т и оценку погрешности. В самом деле, найдем п значений случайной величины  . Очевидно, эта ошибка стремится к нулю с ростом п, что и требовалось доказать.
. Очевидно, эта ошибка стремится к нулю с ростом п, что и требовалось доказать.


