1. Измерение степени связности (тесноты, силы) двух и более явлений. Здесь речь идет в основном о подтверждении уже известных связей.
2. Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения тесноты связи между явлениями.
3. Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей.
Перечислим задачи регрессионного анализа.
1. Установление формы зависимости (линейная или нелинейная; положительная или отрицательная и т. д.).
2. Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов, если бы прочие не изменялись и если бы были исключены случайные элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.
3. Оценка неизвестных значений зависимой переменной, т. е. решение задач экстраполяции и интерполяции. В ходе экстраполяции распространяются тенденции, установленные в прошлом, на будущий период. Экстраполяция широко используется в прогнозировании. В ходе интерполяции определяют недостающие значения, соответствующие моментам времени между известными моментами, т. е. определяют значения зависимой переменной внутри интервала заданных значений факторов.
Рассмотрим подробнее регрессию.
Выборочные уравнения регрессии
Условное математическое ожидание случайной величины У: М(Y/X) есть функция от X, которая называется функцией регрессии и равна f(x), т.е.  ; (4.2)
; (4.2)
аналогично  ; (4.3)
; (4.3)
Графическое изображение f(x) или  называется линией регрессии, а записанные уравнения (4.2) и (4.3) – уравнениями регрессии.
называется линией регрессии, а записанные уравнения (4.2) и (4.3) – уравнениями регрессии.
Поскольку условное математическое ожидание М случайной величины Y есть функция от (х), то его оценка  , т. е. условная средняя, также является функцией от X. Обозначим эту функцию через
, т. е. условная средняя, также является функцией от X. Обозначим эту функцию через
 . (4.4)
. (4.4)
Уравнение (4.4) определяет выборочное уравнение регрессии у на х. Сама функция  называется выборочной регрессией У на X, а график
называется выборочной регрессией У на X, а график  – выборочной регрессией. Аналогично определяется для случайных величин X:
– выборочной регрессией. Аналогично определяется для случайных величин X:
 . (4.5)
. (4.5)
Функция регрессии необратима, так как речь идет о средних величинах для некоторого конкретного значения фактора.
Функция регрессии формально устанавливает соответствие между переменными X и Y, хотя такой зависимости может и не быть в экономике (ложная регрессия).
Линейная регрессия
Пусть задана система случайных величин X н У и случайные величины X и Y зависимы.
Представим одну из случайных величин как линейную функцию другой случайной величины X.
 , (4.6)
, (4.6)
где α, β – параметры, которые подлежат определению.
В общем случае эти параметры могут быть определены различными способами, наиболее часто используется метод наименьших квадратов (МНК).
Функцию g(x) называют наилучшим приближением в смысле МНК, если математическое ожидание  принимает наименьшее возможное значение.
принимает наименьшее возможное значение.
В этом случае функцию g(x) называют средней квадратической регрессией Y на X. Можно доказать, что линейная средняя квадратическая регрессия имеет вид:
 , (4.7)
, (4.7)
где тх, ту — математические ожидания случайных величин X, Y соответственно; σx,σy – средние квадратические отклонения случайных величин X, Y c соответственно; r – коэффициент парной корреляции, который определяется по формуле:
 , (4,8)
, (4,8)
где Mxy – ковариация.
 , (4.9)
, (4.9)
тогда  – коэффициент регрессии. Возникает проблема определения параметров α и β на основе выборки.
– коэффициент регрессии. Возникает проблема определения параметров α и β на основе выборки.
Рассмотрим определение параметров выбранного уравнения прямой линии средней квадратическои регрессии по несгруппированным данным. Пусть изучается система количественных признаков (X, Y), т. е. ведутся наблюдения за двухмерной случайной величиной (X, У). Пусть в результате п наблюдений получено п пар чисел (х1, у1), (х2, у2),..., (хn, уn).
Требуется по полученным данным найти выборочное уравнение прямой линии средней квадратическои регрессии:
 .
.
Поскольку данные несгруппированные, т. е. каждая пара чисел встречается один раз, то можно перейти от условной средней к переменной у. Угловой коэффициент k обозначим через  и назовем его выборочной оценкой коэффициента регрессии
и назовем его выборочной оценкой коэффициента регрессии  .
.
Итак, требуется найти:
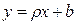 . (4.10)
. (4.10)
Очевидно, параметры  и b нужно подобрать так, чтобы точки (х1, у1), (х2, у2),..., (хn, уn),построенные по исходным данным, лежали как можно ближе к прямой (4.10) (рис. 4.1).
и b нужно подобрать так, чтобы точки (х1, у1), (х2, у2),..., (хn, уn),построенные по исходным данным, лежали как можно ближе к прямой (4.10) (рис. 4.1).

Рис. 4.1. Динамика изменения признака Y
Уточним смысл этого требования. Для этого введем следующее понятие. Назовем отклонением разность вида:
 ,
,
где Yi – вычисляется по уравнению (4.10) и соответствует наблюдаемому значению хi; уi – наблюдаемая ордината, соответствующая хi.
Подберем параметры р и b так, чтобы сумма квадратов указанных отклонений была наименьшей:
В этом состоит требование метода наименьших квадратов (МНК).
Эта сумма есть функция F отыскиваемых параметров р и b:

 .
.
Для отыскания min найдем произвольные и приравняем их к нулю:

Далее запишем систему:

Для простоты вместо  ,
,  ,
,  ,
,  будем писать
будем писать  ,
,  ,
,  ,
, 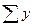 (индекс i опускаем), тогда:
(индекс i опускаем), тогда:

Получили систему двух линейных уравнений относительно р и b. Решая эту систему, получим:
 ; (4.11)
; (4.11)
 . (4.12)
. (4.12)
Метод наименьших квадратов применяется и для нахождения параметров множественной регрессии. В этом случае число линейных уравнений возрастает, и такие системы уравнений решаются с помощью ЭВМ.
Основные понятия корреляционно-регрессионного анализа
1. Среднее значение переменной определяется по следующей формуле:
 , (4.13)
, (4.13)
uде xi – эмпирическое значение переменной x;
n – число наблюдений.
2. Дисперсия
 , (4.14)
, (4.14)
3. Ковариация
 . (4.15)
. (4.15)
4. Коэффициент корреляции
 . (4.16)
. (4.16)
Коэффициент корреляции характеризует тесноту или силу связи между переменными у и х. Значения, принимаемые rxy, заключены в пределах от — 1 до + 1. При положительном значении rху имеет место положительная корреляция, т. е. с увеличением (уменьшением) значений одной переменной (х) значение другой (у) соответственно увеличивается (уменьшается). При отрицательном значении rxv имеет место отрицательная корреляция, т. е. с увеличением (уменьшением) значений х значения у соответственно уменьшаются (увеличиваются). При изучении экономического явления, зависящего от многих факторов, строится множественная регрессионная зависимость. В этом случае для характеристики тесноты связи используется коэффициент множественной корреляции:
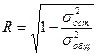 . (4.17)
. (4.17)
где 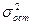 – остаточная дисперсия зависимой переменной;
– остаточная дисперсия зависимой переменной;
 – общая дисперсия зависимой переменной.
– общая дисперсия зависимой переменной.
5. Общая дисперсия определяется по формуле:
 . (4.18)
. (4.18)
Величина  характеризует разброс наблюдений фактических значений
характеризует разброс наблюдений фактических значений  .
.
6. Остаточная дисперсия определяется по следующей формуле:

 , (4.19)
, (4.19)
где  – теоретические значения переменной у, полученные по уравнению регрессии (4.1) при подстановке в него наблюдаемых фактических значений xi.
– теоретические значения переменной у, полученные по уравнению регрессии (4.1) при подстановке в него наблюдаемых фактических значений xi.
Остаточная дисперсия характеризует ту часть рассеяния переменной у, которая возникает из-за всякого рода случайностей и влияния неучтенных факторов.
7. Коэффициент детерминации служит для оценки точности регрессии, т. е. соответствия полученного уравнения регрессии имеющимся эмпирическим данным, и вычисляется по формуле
 . (4.20)
. (4.20)
Изменяется Д в пределах от 0 до 1, т.е.  .
.
Модель считается тем точнее, чем ближе Д к 1, т.е. чем меньше 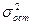 .
.
Стандартная ошибка оценки равна  .
.
Если Д = 0, это значит, что отношение  =1, т.е.
=1, т.е.  , и, следовательно,
, и, следовательно,  . В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если Д = 1, это значит, что отношение
. В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если Д = 1, это значит, что отношение  = 0, т.е.
= 0, т.е.  , и, следовательно,
, и, следовательно,  , т.е все наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.
, т.е все наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.
8. Корреляционное отношение используется для оценки тесноты связи между двумя явлениями, в частности для определения тесноты связи исходного ряда щ с теоретическим рядом yh. Корреляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле:
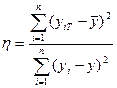 . (4.21)
. (4.21)
4.2. Исходные предпосылки регрессионного анализа
и свойства оценок
Применение метода наименьших квадратов для определения параметров регрессии предполагает выполнение некоторых предпосылок(Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа. – М.: Финансы и статистика, 1983).
Отметим наиболее существенные из них.
Предпосылка 1. При нахождении оценок переменной у предполагается существование зависимости переменной у только от тех объясняющих переменных, которые вошли в модель (регрессию). Влияние прочих факторов и случайностей учитывается случайной возмущающей переменной z При этом полагаем, что для фиксированных значений переменных  среднее значение переменной z равно нулю.
среднее значение переменной z равно нулю.
Предпосылка 2. Предполагается, что влияние неучтенных факторов постоянно. Так, при рассмотрении временных рядов в различные периоды эти неучтенные факторы оказывают одинаковое влияние.
Предпосылка 3. Отсутствует автокорреляция между возмущающими переменными z.
Предпосылка 4. Число наблюдений должно превышать число параметров регрессии, иначе невозможна оценка этих параметров.
Предпосылка 5. Предполагается односторонняя зависимость переменной у от факторов  , отсутствие взаимосвязи.
, отсутствие взаимосвязи.
Предпосылка 6. Зависимая переменная у и факторы  распределены нормально.
распределены нормально.
С помощью регрессионного анализа при указанных выше предпосылках находят оценки параметров, наиболее хорошо согласующиеся с опытными данными. Данные оценки должны обладать определенными свойствами. Рассмотрим некоторые из этих свойств (без доказательства).
1. Несмещенность оценок параметров регрессии. Оценка параметров регрессии называется несмещенной, если для любого фиксированного числа наблюдений выполняется равенство математического ожидания параметра и значения параметра регрессии. Надо отметить, что оценки, полученные методом наименьших квадратов, обладают свойством несмещенности.
2. Состоятельность оценок параметров регрессии. Данное свойство состоит в том, что с ростом объема выборки оценка параметра регрессии b сходится к теоретическому значению параметра β (вычисленного по всей генеральной совокупности), т. е. ошибка оценки стремится к нулю:
 . (4.22)
. (4.22)
3. Эффективность оценок параметров регрессии. Несмещенная оценка параметра регрессии называется несмещенной эффективной, если она среди всех прочих несмещенных оценок этого же параметра обладает наименьшей дисперсией.
4. Достаточность оценки. Если β представляет собой достаточную оценку параметра b, то не существует другой оценки этого параметра, которую можно получить по выборке из некоторой генеральной совокупности и которая дала бы дополнительную информацию о нем. Р. Фишер показал, что количество измеримой информации, содержащейся в некоторой оценке, равно обратной величине от ее дисперсии. Таким образом, понятие достаточности эквивалентно требованию минимальной дисперсии. Достаточная оценка с необходимостью должна быть эффективной и, следовательно, также состоятельной и несмещенной.
4.3. Этапы построения многофакторной корреляционной
регрессионной модели
Разработка модели и исследование экономических процессов должны выполняться по следующим этапам.
1. Априорное исследование экономической проблемы.
2. Формирование перечня факторов и их логический анализ.
3. Сбор исходных данных и их первичная обработка.
4. Спецификация функции регрессии.
5. Оценка функции регрессии.
6. Отбор главных факторов.
7. Проверка адекватности модели.
8. Экономическая интерпретация.
9. Прогнозирование неизвестных значений зависимой пере
менной.
Рассмотрим подробнее содержание этапов.
1. Априорное исследование экономической проблемы.
В соответствии с целью работы на основе знаний макро- и микроэкономики конкретизируются явления, процессы, зависимость между которыми подлежит оценке. При этом подразумевается прежде всего четкое определение экономических явлений, установление объектов и периода исследования.
На этом этапе исследования должны быть сформулированы экономически осмысленные и приемлемые гипотезы о зависимости экономических явлений.
2. Формирование перечня факторов и их логический анализ.
Для определения наиболее разумного числа переменных в регрессионной модели прежде всего ориентируются на соображения профессионально-теоретического характера. Исходя из физического смысла явления, производят классификацию переменных на зависимую и объясняющую.
3. Сбор исходных данных и их первичная обработка.
При построении модели исходная информация может быть собрана в трех видах:
Ø динамические (временные) ряды;
Ø пространственная информация — информация о работе нескольких объектов в одном разрезе времени;
Ø сменная - табличная форма. Информация о работе нескольких объектов за разные периоды.
Объем выборки зависит от числа факторов, включаемых в модель с учетом свободного члена. Для получения статистически значимой модели требуется на один фактор объем выборки, равный  наблюдений. Например, если в модель включаются три фактора, то минимальный объем выборки
наблюдений. Например, если в модель включаются три фактора, то минимальный объем выборки
 ,
,
где т – число факторов, включаемых в модель; п – число свободных членов в уравнении.
Если в квартальном разрезе собирать данные, то надо их собирать за 5 лет [20/4].
4. Спецификация функции регрессии.
На данном этапе исследования дается конкретная формулировка гипотезы о форме связи (линейная или нелинейная, простая или множественная и т. д.). Для этого используются различные критерии для проверки состоятельности гипотетического вида зависимости. На этом этапе проверяются предпосылки корреляционно-регрессионного анализа.
5. Оценка функции регрессии.
Здесь определяются числовые значения параметров регрессии и вычисление ряда показателей, характеризующих точность регрессионного анализа.
6. Отбор главных факторов.
Выбор факторов – основа для построения многофакторной корреляционно-регрессионной модели.
На этапе «Формирование перечня факторов и их логический анализ» собираются все возможные факторы, обычно более 20–30 факторов. Но это неудобно для анализа, и модель, включающая 20–30 факторов, будет неустойчива. Неустойчивость модели находит выражение в том, что в ней изменение некоторых факторов ведет к увеличению у вместо снижения у.
Мало факторов – тоже плохо. Это может привести к ошибкам при принятии решений в ходе анализа модели. Поэтому необходимо выбирать более рациональный перечень факторов. При этом проводят анализ факторов на мультиколлинеарность.



 ; (4.2)
; (4.2) ; (4.3)
; (4.3) называется линией регрессии, а записанные уравнения (4.2) и (4.3) – уравнениями регрессии.
называется линией регрессии, а записанные уравнения (4.2) и (4.3) – уравнениями регрессии. , т. е. условная средняя, также является функцией от X. Обозначим эту функцию через
, т. е. условная средняя, также является функцией от X. Обозначим эту функцию через . (4.4)
. (4.4) называется выборочной регрессией У на X, а график
называется выборочной регрессией У на X, а график  . (4.5)
. (4.5) , (4.6)
, (4.6) принимает наименьшее возможное значение.
принимает наименьшее возможное значение. , (4.7)
, (4.7) , (4,8)
, (4,8) , (4.9)
, (4.9) – коэффициент регрессии. Возникает проблема определения параметров α и β на основе выборки.
– коэффициент регрессии. Возникает проблема определения параметров α и β на основе выборки. .
. и назовем его выборочной оценкой коэффициента регрессии
и назовем его выборочной оценкой коэффициента регрессии 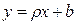 . (4.10)
. (4.10) и b нужно подобрать так, чтобы точки (х1, у1), (х2, у2),..., (хn, уn),построенные по исходным данным, лежали как можно ближе к прямой (4.10) (рис. 4.1).
и b нужно подобрать так, чтобы точки (х1, у1), (х2, у2),..., (хn, уn),построенные по исходным данным, лежали как можно ближе к прямой (4.10) (рис. 4.1).
 ,
,
 .
.

 ,
,  ,
,  ,
,  будем писать
будем писать  ,
,  ,
,  ,
, 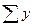 (индекс i опускаем), тогда:
(индекс i опускаем), тогда:
 ; (4.11)
; (4.11) . (4.12)
. (4.12) , (4.13)
, (4.13) , (4.14)
, (4.14) . (4.15)
. (4.15) . (4.16)
. (4.16)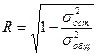 . (4.17)
. (4.17)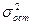 – остаточная дисперсия зависимой переменной;
– остаточная дисперсия зависимой переменной; – общая дисперсия зависимой переменной.
– общая дисперсия зависимой переменной. . (4.18)
. (4.18)
 , (4.19)
, (4.19) – теоретические значения переменной у, полученные по уравнению регрессии (4.1) при подстановке в него наблюдаемых фактических значений xi.
– теоретические значения переменной у, полученные по уравнению регрессии (4.1) при подстановке в него наблюдаемых фактических значений xi. . (4.20)
. (4.20) .
. .
. =1, т.е.
=1, т.е.  , и, следовательно,
, и, следовательно,  . В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если Д = 1, это значит, что отношение
. В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если Д = 1, это значит, что отношение  , и, следовательно,
, и, следовательно,  , т.е все наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.
, т.е все наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.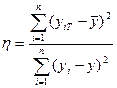 . (4.21)
. (4.21) среднее значение переменной z равно нулю.
среднее значение переменной z равно нулю. . (4.22)
. (4.22) наблюдений. Например, если в модель включаются три фактора, то минимальный объем выборки
наблюдений. Например, если в модель включаются три фактора, то минимальный объем выборки ,
,


