Для моделирования случайной величины необходимо знать ее закон распределения. Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, в основе которого лежит их формирование из исходной последовательности случайных чисел, распределенных в интервале [0,1] по равномерному закону.
Равномерно распределенные в интервале [0,1] последовательности случайных чисел можно получить тремя способами:
Ø использование таблиц случайных чисел;
Ø применение генераторов случайных чисел;
Ø метод псевдослучайных чисел.
При решении задачи без применения ЭВМ чаще всего используют таблицы случайных чисел. В таблицах случайных чисел случайные цифры имитируют значения дискретной случайной величины с равномерным распределением:

При составлении таких таблиц выполняется требование, чтобы каждая из этих цифр от 0; 1;...; 9 встречалась примерно одинаково часто и независимо от других с вероятностью  .
.
Самая большая из опубликованных таблиц случайных чисел содержит 1 000 000 цифр. Таблицы случайных чисел составить не так просто. Они требуют тщательной проверки с помощью специальных статистических тестов.
При решении задач на ЭВМ для выработки случайных чисел, равномерно распределенных в интервале [0,1|, могут применяться генераторы случайных чисел. Данные генераторы преобразуют результаты случайного физического процесса в двоичные числа. В качестве случайного физического процесса обычно используют собственные шумы (случайным образом меняющееся напряжение).
Недостатки данного способа получения случайных чисел следующие:
1. Трудно проверить качество вырабатываемых чисел.
2. Случайные числа не воспроизводимы (если их не запоминать), и, как следствие, нельзя повторить расчет на ЭВМ для исключения случайного сбоя.
Получение псевдослучайных чисел с равномерным законом распределения заключается в выработке псевдослучайных чисел. Псевдослучайные числа – это числа, полученные по какой-либо формуле и имитирующие значения случайной величины. Под словом «имитирующие» подразумевается, что эти числа удовлетворяют ряду тестов так, как если бы они были значениями этой случайной величины.
Первый алгоритм для получения псевдослучайных чисел предложил Дж. Нейман. Это так называемый метод середины квадратов, который заключается в следующем:


 и т.д.
и т.д.
Алгоритм себя не оправдал: получилось больше, чем нужно, малых значений γi – случайных чисел. В настоящее время разработано множество алгоритмов для получения псевдослучайных чисел.
Назовем достоинства метода псевдослучайных чисел.
1. На получение каждого случайного числа затрачивается несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ.
2. Малый объем памяти ЭВМ для программирования.
3. Любое из чисел легко воспроизвести.
4. Качество генерируемых случайных чисел достаточно проверить один раз.
Подавляющее число расчетов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. От последовательности случайных чисел, равномерно распределенных в интервале [0,1], нетрудно перейти к последовательности случайных чисел с произвольным заданным законом распределения.
Существует основное соотношение, связывающее случайные числа с заданным законом распределения и случайные числа с равномерным законом распределения в интервале [0,1]. Суть его состоит в том, что для преобразования последовательности случайных чисел с равномерным законом распределения в интервале [0,1] в последовательность случайных чисел с заданной функцией распределения F(x) необходимо из совокупности случайных чисел с равномерным законом распределения в интервале [0,1] выбрать случайное число  , и решить уравнение:
, и решить уравнение:
 (3.5)
(3.5)
относительно х.
Решение уравнения представляет собой случайное число из совокупности случайных чисел, имеющих функцию распределения F(x),
В случае, когда вместо функции распределения F(x) задана плотность вероятности f(х), соотношение (3.5) принимает вид:
 (3.6)
(3.6)
Для ряда законов распределения, наиболее часто встречающихся в реальной экономике, получено аналитическое решение уравнения (3.6), результаты которого приведены в табл. 3.1.
| Закон распределения случайной величины
| Плотность распределения
| Формула для моделирования случайной величины
|
| Экспоненциальный
| 
| 
|
| Вейбула
| 
| 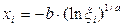
|
| Гамма-распределение
(η – целые числа)
| 
| 
|
| Нормальное
| 
| 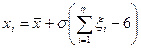
|
Параметры закона распределения Вейбула выбираются по таблицам приложения.
Пример 3.1. В результате статистической обработки экспериментальных данных получены следующие значения характеристик случайной величины X:  = 40,7 и
= 40,7 и 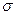 = 30,2. Установлено, что величина X распределена в соответствии с законом Вейбула.
= 30,2. Установлено, что величина X распределена в соответствии с законом Вейбула.
Определите параметры данного закона.
Решение.
1. Вычислим коэффициент вариации случайной величины X:
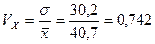 .
.
2. Исходя из значения коэффициента вариации, определим по
таблицам приложения параметры а и Са. Величины параметров при
V = 0,742 равны а = 1,4; Са = 0,659.
3. Вычислим параметр b по формуле:
 . (3.7)
. (3.7)
Параметры гамма-распределения вычислим по следующим формулам:
 ; (3.8)
; (3.8)  . (3.9)
. (3.9)
Пример 3.2. Время обслуживания пассажира в кассе Аэрофлота подчинено гамма-распределению. При этом известно среднее значение времени обслуживания  = 42 мин.; среднее квадрата чес кое отклонение времени равно 14,8 мин.
= 42 мин.; среднее квадрата чес кое отклонение времени равно 14,8 мин.
Вычислите параметры закона распределения.
Решение
1. Вычислим параметр 
 .
.
2. Величину параметра \] определим по следующей формуле:
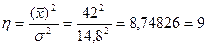
Пример 3.3. Для ПК интенсивность потока отказов  = 1,2 отк/сутки. Требуется определить последовательность значений продолжительности интервалов между отказами ПК. Известно, что эти интервалы описываются показательным законом распределения.
= 1,2 отк/сутки. Требуется определить последовательность значений продолжительности интервалов между отказами ПК. Известно, что эти интервалы описываются показательным законом распределения.
Решение
Определим продолжительность интервала между отказами  , используя формулу для моделирования случайной величины, распределенной в соответствии с экспоненциальным законом:
, используя формулу для моделирования случайной величины, распределенной в соответствии с экспоненциальным законом:
 .
.
Значения 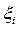 определим по таблицам случайных чисел.
определим по таблицам случайных чисел.
Допустим  = 0,7182;
= 0,7182;  = 0,4365;
= 0,4365;  = 0,1548;
= 0,1548;  = 0,8731.
= 0,8731.
Тогда
 суток;
суток;
 суток;
суток;
 суток;
суток;
 суток;
суток;




 .
.

 и т.д.
и т.д. , и решить уравнение:
, и решить уравнение: (3.5)
(3.5) (3.6)
(3.6)


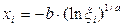



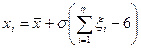
 = 40,7 и
= 40,7 и 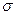 = 30,2. Установлено, что величина X распределена в соответствии с законом Вейбула.
= 30,2. Установлено, что величина X распределена в соответствии с законом Вейбула.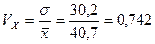 .
. . (3.7)
. (3.7) ; (3.8)
; (3.8)  . (3.9)
. (3.9) = 42 мин.; среднее квадрата чес кое отклонение времени равно 14,8 мин.
= 42 мин.; среднее квадрата чес кое отклонение времени равно 14,8 мин.
 .
.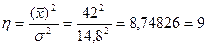
 , используя формулу для моделирования случайной величины, распределенной в соответствии с экспоненциальным законом:
, используя формулу для моделирования случайной величины, распределенной в соответствии с экспоненциальным законом: .
.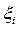 определим по таблицам случайных чисел.
определим по таблицам случайных чисел. = 0,7182;
= 0,7182;  = 0,4365;
= 0,4365;  = 0,1548;
= 0,1548;  = 0,8731.
= 0,8731. суток;
суток; суток;
суток; суток;
суток; суток;
суток;

