При использовании метода моделирования свойства и поведение объекта изучают путем применения вспомогательной системы – модели, находящейся в определенном объективном соответствии с исследуемым объектом.
Представления о тех или иных свойствах объектов, их взаимосвязях формируются исследователем в виде описания этих объектов на обычном языке, в виде рисунков, графиков, формул или реализуются в виде макетов и других устройств. Подобные способы описания обобщаются в едином понятии – модель, а построение и изучение моделей называется моделированием.
Модель – объект любой природы, который создается исследователем с целью получения новых знаний об объекте-оригинале и отражает только существенные (с точки зрения разработчика) свойства оригинала.
Модель считается адекватной объекту-оригиналу, если она с достаточной степенью приближения на уровне понимания моделируемого процесса исследователем отражает закономерности процесса функционирования реальной системы во внешней среде.
Модели позволяют вынести упрощенное представление о системе и получить некоторые результаты намного проще, чем при изучении реального объекта. Более того, гипотетически модели объекта могут быть исследованы и изучены перед тем, как объект будет создан.
В практике исследования производственно-экономических объектов модели могут применяться для самых разных целей, что вызывает использование моделей различных классов. Построение одной-единственной математической модели для сложной производственной системы практически не представляется возможным без разработки вспомогательных моделей. Поэтому, как правило, при создании конечной математической модели исследуемого объекта строят частные вспомогательные модели, отражающие ту или иную информацию об объекте, имеющуюся у разработчика на данном этапе построения модели.
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.
Классификационные признаки. В качестве одного из первых признаков классификации видов моделирования можно выбрать степень полноты модели и разделить модели в соответствии с этим признаком на полные, неполные и приближенные. В основе полного моделирования лежит полное подобие, которое проявляется как во времени, так и в пространстве. Для неполного моделирования характерно неполное подобие модели изучаемому объекту. В основе приближенного моделирования лежит приближенное подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем. Классификация видов моделирования систем S приведена на рис.1.1.
В зависимости от характера изучаемых процессов в системе S все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, а динамическое моделирование отражает поведение объекта во времени. Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется для тех случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.














Рис. 1.1. Классификация видов моделирования систем
В зависимости от формы представления объекта (системы S) можно выделить мысленное и реальное моделирование.
Мысленное моделирование часто является единственным способом моделирования объектов, которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания.
При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте.
Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков и символов.
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.
Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифферен-циальных, конечно-разностных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
Желая использовать аналитический метод, часто идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Аналитические методы бывают детерминированные и статистические. Численный метод проведения аналитических расчетов с помощью датчиков случайных чисел получил название метода статистических испытаний, или метода Монте-Карло.
При алгоритмическом моделировании описывается процесс функционирования системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Аналитические модели также могут быть детерминированными и статистическими. В последнем случае в модели с помощью датчиков случайных чисел имитируется действие неопределенных и случайных факторов. Такой метод моделирования получил наименование метода статистического моделирования. В настоящее время этот метод считается наиболее эффективным методом исследования сложных систем, а часто и единственным практически доступным методом получения информации о поведении гипотетической системы на этапе ее проектирования.
Комбинированное моделирование позволяет объединить достоинства аналитического и алгоритмического моделирования. При построении комбинированных моделей производится предварительная декомпозиция процесса функционирования модели на составляющие подпроцессы. Для тех из них, где это возможно, используются аналитические модели, а для остальных процессов строятся алгоритмические модели.
Насколько можно судить по литературным источникам общепринятой классификации моделей экономических систем пока не существует. Однако представляется достаточно полезной классификация математических моделей экономических систем, приведенная в книге Т. Нейлора «Машинные имитационные эксперименты с моделями экономических систем» (1971 г.) (рис. 1.2).
Экономико-математической моделью (ЭММ) называется выражение, состоящее из совокупности связанных между собой математическими зависимостями (формулами, уравнениями, неравенствами, логическими условиями величин – факторов, все или часть которых имеют экономический смысл. По своей роли в ЭММ эти факторы целесообразно подразделить на параметры и характеристики (рис. 1.3).
При этом параметрами объекта называются факторы, характеризующие свойства объекта или составляющих его элементов. В процессе исследования объекта ряд параметров может изменяться, поэтому они называются переменными, которые в свою очередь подразделяются на переменныесостояния и переменныеуправления. Как правило, переменные состояния объекта являются функцией переменных управления и воздействий внешней среды.

Рис.1.2. Классификация экономических моделей


Рис. 1.3. Классификация факторов по их роли в ЭВМ
Характеристиками (выходными характеристиками) называются интересующие исследователя непосредственные конечные результаты функционирования объекта (естественно, что выходные характеристики являются переменными состояния). Соответственно характеристики внешней среды описывают свойства внешней среды, которые сказываются на процессе и результате функционирования объекта. Значения ряда факторов, определяющие начальное состояние объекта или внешней среды, называются начальными условиями.
При рассмотрении ЭММ оперируют следующими понятиями: критерий оптимальности, целевая функция, система ограничений, уравнения связи, решение модели.
Критерием оптимальности называется некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции через факторы модели. Критерий оптимальности определяет смысловое содержание целевой функции.
Целевая функция математически связывает между собой факторы модели, ее значение определяется значениями этих величин. Содержательный смысл целевой функции придает только критерий оптимальности.
Не следует смешивать критерий оптимальности и целевую функцию. Так, например, критерий прибыли и стоимости произведенной продукции могут описываться одной и той же целевой функцией:
 , (1.1)
, (1.1)
где  – номенклатура производимой продукции;
– номенклатура производимой продукции;  – объем выпуска i -ой номенклатуры;
– объем выпуска i -ой номенклатуры;  – прибыль от выпуска единицы i -ой номенклатуры или стоимость единицы i -ой номенклатуры в зависимости от смысла критерия оптимальности.
– прибыль от выпуска единицы i -ой номенклатуры или стоимость единицы i -ой номенклатуры в зависимости от смысла критерия оптимальности.
Критерий прибыли может рассчитываться и по нелинейной целевой функции:
 , (1.2)
, (1.2)
Если прибыль от выпуска единицы i -ой номенклатуры является функцией от объема выпуска  .
.
При наличии нескольких критериев оптимальности каждый из них будет формализован своей частной целевой функцией  , где
, где 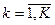 – число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию
– число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию
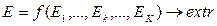 . (1.3)
. (1.3)
Однако целевая функция может уже не нести экономического смысла, в этом случае критерий оптимальности для нее отсутствует.
Система ограничений определяет пределы, сужающие область осуществимых, приемлемых или допустимых решений и фиксирующие основные внешние и внутренние свойства объекта. Ограничения определяют область протекания процесса, пределы изменения параметров и характеристик объекта.
Уравнения связи являются математической формализацией системы ограничений.
Критерий оптимальности и система ограничений в первую очередь определяют концепцию построения будущей математической модели, т.е. концептуальную модель, а их формализация, т.е. целевая функция и уравнения связи, представляют собой математическую модель.
Решением математической модели называется такой набор (совокупность) значений переменных, который удовлетворяет ее уравнениям связи. Решения, имеющие экономический смысл, называют структурно допустимыми. Модели, имеющие много решений, называются вариантными в отличие от безвариантных, имеющих одно решение. Среди структурно допустимых решений вариантной модели, как правило, находится одно решение, при котором целевая функция в зависимости от смысла модели имеет наибольшее или наименьшее значение. Такое решение, как и соответствующее значение целевой функции, называется оптимальным (в частности, наименьшим или наибольшим).
Выбор метода решения оптимизационных ЭММ зависит от математической формы, связывающей факторы модели, наличия тех или иных признаков (учет динамики, учет стохастичности и т.д.).
По характеру цели исследования ЭММ делятся на оптимизационные (нормативные) и описательные (дескриптивные или ЭММ прямого счета).
Характерной чертой оптимизационных моделей является наличие одной или нескольких целевых функций. При этом в первом случае оптимизационные ЭММ называются монокритериальными, а во втором – многокритериальными. В общем виде монокритериальная ЭММ может быть представлена следующей системой отношений:
 ; (1.4)
; (1.4)
 , (1.5)
, (1.5)
где Е – критерий оптимальности объекта;  – управляемые переменные,
– управляемые переменные,  ;
;  – неуправляемые факторы модели;
– неуправляемые факторы модели;  ;
;  – уравнения связи, представляющие собой формализацию системы ограничений,
– уравнения связи, представляющие собой формализацию системы ограничений,  ;
;  – целевая функция – формализованное выражение критерия оптимальности.
– целевая функция – формализованное выражение критерия оптимальности.
Выражение 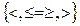 означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий.
означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий.
Решение модели, заданной соотношениями (1.4) и (1.5), заключается в нахождении совокупности значений переменных
 ,
,
обращающий в max (или min) целевую функцию Е при заданных уравнениях связи  .
.
Специфика конкретных задач управления производством определила разнообразие типов оптимизационных ЭММ. Это вызвало для ряда наиболее часто повторяющихся типов ситуаций разработку «стандартных» экономико-математических методов их описания, например, распределительные задачи различных классов, задачи управления запасами, ремонта и замены оборудования, проектирования сетей и выбора маршрутов и т.д.
Существенным признаком описательных моделей является отсутствие в них критерия оптимальности. Решение, даваемое ЭММ прямого счета, обеспечивает либо вычисление набора выходных характеристик объекта для одного или нескольких вариантов начальных условий и входных характеристик объекта, либо нахождение какой-либо совокупности значений в структурно допустимой области решений.
В зависимости от степени формализованности связей f и gi между факторами моделей в выражениях (1.4) и (1.5) различают аналитические и алгоритмические модели.
В расширение представленного ранее отметим, что аналитической формой записи называется запись математической модели в виде алгебраических уравнений или неравенств, не имеющих разветвлений вычислительного процесса при определении значений любых переменных состояния модели, целевой функции и уравнений связи. Если в математических моделях единственная целевая функция f и ограничения gj заданы аналитически, то подобные модели относятся к классу моделей математического программирования. Характер функциональных зависимостей, выраженных в функциях f и gj, может быть линейным и нелинейным. Соответственно этому ЭММ делятся на линейные и нелинейные, а среди последних в специальные классы выделяются дробно-линейные, кусочно-линейные, квадратичные и выпуклые модели.
В зависимости от того, содержит ли ЭММ случайные факторы, она может быть отнесена к классу стохастических или детерминированных.
В детерминированных моделях ни целевая функция f, ни уравнения связи gj не содержат случайных факторов. Следовательно, для данного множества входных значений модели на выходе может быть получен только один-единственный результат. Для стохастических ЭММ характерно наличие среди факторов  модели, описываемой соотношениями (1.4) и (1.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.
модели, описываемой соотношениями (1.4) и (1.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.
Следующим признаком, по которому можно различать ЭММ, является связь с фактором времени. Модели, в которых входные факторы, а, следовательно, и результаты моделирования явно зависят от времени, называются динамическими, а модели, в которых зависимость от времени t либо отсутствует совсем, либо проявляется слабо или неявно, называют статическими.






















 , (1.1)
, (1.1) – номенклатура производимой продукции;
– номенклатура производимой продукции;  – объем выпуска i -ой номенклатуры;
– объем выпуска i -ой номенклатуры;  – прибыль от выпуска единицы i -ой номенклатуры или стоимость единицы i -ой номенклатуры в зависимости от смысла критерия оптимальности.
– прибыль от выпуска единицы i -ой номенклатуры или стоимость единицы i -ой номенклатуры в зависимости от смысла критерия оптимальности. , (1.2)
, (1.2) , где
, где 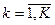 – число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию
– число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию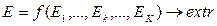 . (1.3)
. (1.3) ; (1.4)
; (1.4) , (1.5)
, (1.5) – неуправляемые факторы модели;
– неуправляемые факторы модели;  ;
;  – уравнения связи, представляющие собой формализацию системы ограничений,
– уравнения связи, представляющие собой формализацию системы ограничений,  ;
;  – целевая функция – формализованное выражение критерия оптимальности.
– целевая функция – формализованное выражение критерия оптимальности.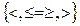 означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий.
означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий. ,
, модели, описываемой соотношениями (1.4) и (1.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.
модели, описываемой соотношениями (1.4) и (1.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.


