Задание 11. Вычисление площади плоской фигуры, ограниченной линиями, заданными параметрическими уравнениями.

Если фигура ограничена кривой, заданной параметрическими уравнениями, то площадь вычисляется по формуле:

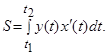
Пример. Вычислить площадь эллипса, заданного параметрическими уравнениями: .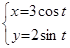

Решение. Дан эллипс с полуосями: большая — 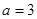, малая — 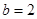. Сделаем чертеж к задаче (рис.4).

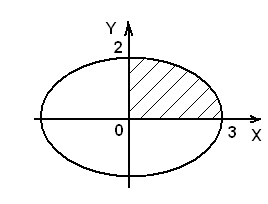
Рис. 4

В силу симметричности фигуры вычислим 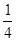 площади. Найдем пределы интегрирования:

так как , то ;

.

.

.

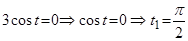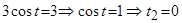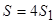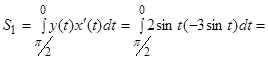
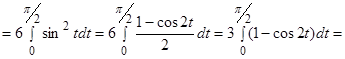
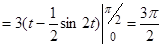Следовательно, площадь 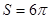(кв.ед.).

 

Задание 12. Вычисление площади плоской фигуры, ограниченной линиями, заданными в полярных координатах.

В полярной системе координат элементарной фигурой является кри­­­­во­­­­­ли­­­­ней­­­ный сектор (рис.5), площадь которого вычисляется по формуле:

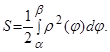
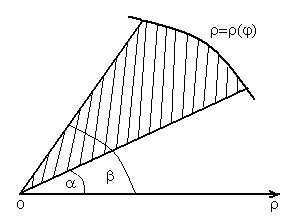
Рис. 5

 

Пример. Найти площадь фигуры, ограниченной линией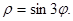

Решение. Так как 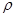 определяет расстояние до соответствующей точки, то 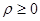. Следовательно, область определения функции определяется неравенством 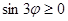. Общее решение этого неравенства имеет вид:

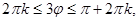 где .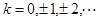

Отсюда 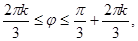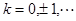. Так как в полярной системе координат выполняются ограничения на область изменения 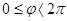, то область допустимых значений функции  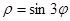в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:

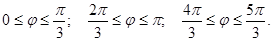
Выбрав несколько значений 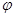 из указанных промежутков, построим график функции (рис. 6).

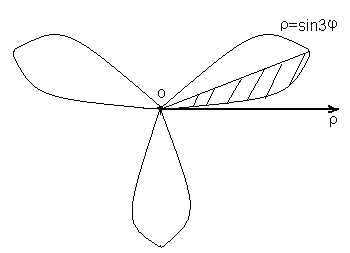
Рис.6

В силу симметричности фигуры вычислим 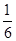 площади, где полярный угол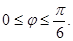

.

.

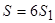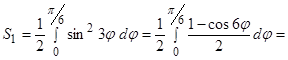
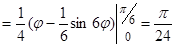Следовательно, площадь всей фигуры 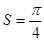(кв.ед.).

 

Задание 13. Вычисление длины дуги кривой, заданной параметрическими уравнениями.

Длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле:

.

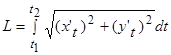Замечание. При вычислении длины кривой, заданной параметрическими уравнениями, нижний предел интегрирования должен быть меньше верхнего предела интегрирования.

Пример. Вычислить длину дуги астроиды, заданной уравнениями:

.

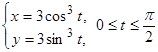Решение.

Вычислим производные функций:

.

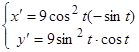Вычислим подынтегральную функцию:

.

.

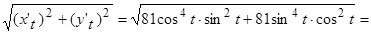
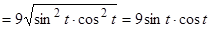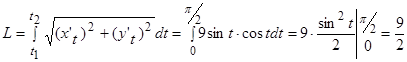Следовательно, длина дуги 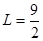(ед.).

 

Задание 14. Вычисление объема тела, образованного вращением фигуры, ограниченной линиями в декартовых координатах.

Пусть дана криволинейная трапеция, ограниченная линиями 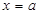, , 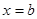, , 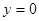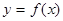где - непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:

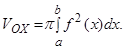
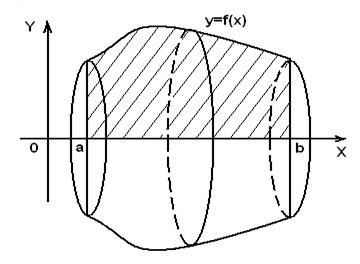
Рис.7

Если криволинейную трапецию, ограниченную линиями 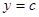, , 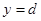, , где 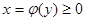- непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:

 

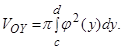
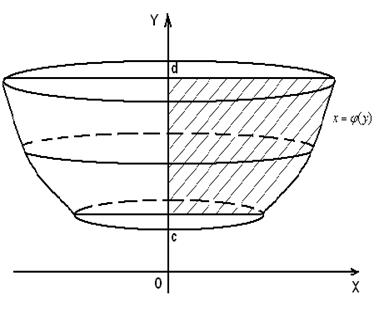
Рис.8

 

Пусть дана криволинейная трапеция, ограниченная линиями 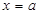, , 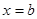, , 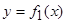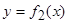где 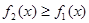(рис.9), то объем полученного тела вращения вычисляется по формуле:

.

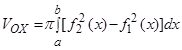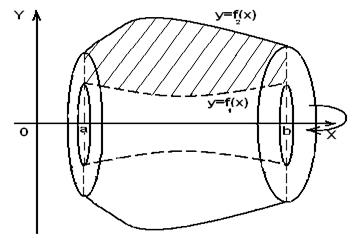
Рис.9

 

Пример. Криволинейная трапеция, ограниченная осью абсцисс и кривой 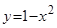 вращается вокруг оси 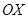. Найти объем полученного тела вращения.

Решение. На рис.10 изображена криволинейная трапеция, которая вращается вокруг оси .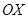

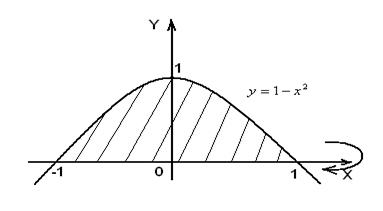
Рис.10

Точки пересечения кривой 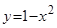 с осью : .

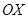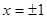Следовательно, пределы интегрирования: .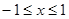

Искомый объем тела вращения:

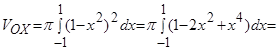
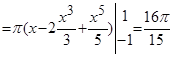(куб.ед.).

 

Пример. Криволинейная трапеция, ограниченная осью ординат и кривой 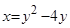вращается вокруг оси 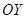. Найти объем полученного тела вращения.

Решение. На рис.11 изображена криволинейная трапеция, которая вращается вокруг оси .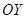                                                        

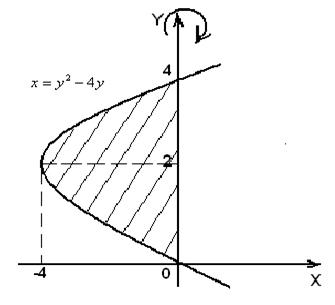
Рис.11

Кривая 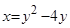 — это парабола с вершиной (-4;2), которая пересекает ось ординат в точках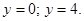

Следовательно, пределы интегрирования: .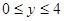

Искомый объем тела вращения:

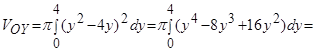
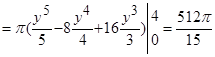 (куб. ед.).

 

Пример. Фигура, ограниченная линиям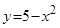и  и 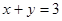,вращается вокруг 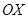. Найти объем полученного тела вращения.

Решение. На рис.12 изображена фигура, которая вращается вокруг оси .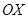  

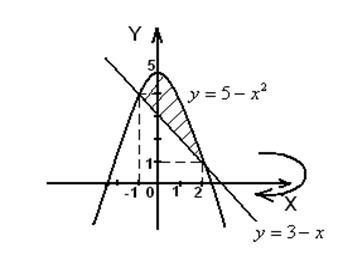
Рис.12

Точки пересечения параболы 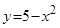 и прямой .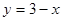

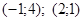Следовательно, пределы интегрирования: .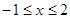

Искомый объем тела вращения вычислим по формуле:

.

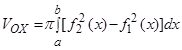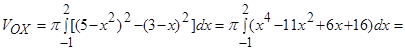
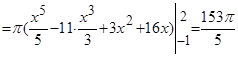 (куб. ед.).